多元求積公式在布朗片測(cè)度下的平均誤差

董彥琦，許貴橋

(天津師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，天津 300387)

多元求積公式在布朗片測(cè)度下的平均誤差

董彥琦，許貴橋

(天津師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，天津 300387)

討論了基于Chebyshev節(jié)點(diǎn)的多元Lagrange求積公式在布朗片測(cè)度下的平均誤差，得到了相應(yīng)量的強(qiáng)漸近階.在多元情形下，構(gòu)造性地建立了平均框架下有關(guān)數(shù)值求積公式的誤差分析，提出的算法更加簡(jiǎn)單適用，且具有一定的收斂速度.

Chebyshev節(jié)點(diǎn)；布朗片測(cè)度；平均誤差；多元求積公式

1 預(yù)備知識(shí)

信息基復(fù)雜度是目前函數(shù)逼近論研究的熱點(diǎn)問題之一，其核心是研究信息基算子的構(gòu)造和誤差.信息基算子是指利用目標(biāo)函數(shù)的若干個(gè)已知信息(主要是函數(shù)在某些點(diǎn)的值，稱為標(biāo)準(zhǔn)信息)來構(gòu)造問題的近似解.但在誤差估計(jì)中，由于目標(biāo)函數(shù)除已知的若干個(gè)信息之外，其他信息均不明確，只能對(duì)目標(biāo)函數(shù)作某些假設(shè)，然后根據(jù)此假設(shè)來探討算法的誤差.在平均框架下，假設(shè)目標(biāo)函數(shù)為一個(gè)函數(shù)概率空間，算法的誤差為空間的個(gè)體元素逼近誤差的期望值.下面引入算法的平均誤差[1]定義.

假設(shè)F是定義在一個(gè)函數(shù)類上的線性賦范空間，G是一個(gè)范數(shù)為‖·‖的Banach空間，μ是定義在F的Borel子集上的概率測(cè)度.稱：F到G的可測(cè)映射S為解算子；F到Rn的一個(gè)可測(cè)映射N為信息算子；Rn到G的一個(gè)可測(cè)映射φ為算法.信息基算子逼近φ°N相應(yīng)于測(cè)度μ的平均誤差定義為

(1)

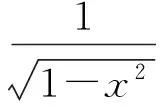
數(shù)值問題的平均誤差分析起始于Suldin[2-3]，之后許多學(xué)者進(jìn)行了大量研究，有關(guān)一元函數(shù)和多元函數(shù)的結(jié)果可見文獻(xiàn)[4-5].注意到多元積分逼近研究所用的方法大多是非確定性的，本文將利用基于第一類切比雪夫多項(xiàng)式零點(diǎn)的拉格朗日求積公式給出相應(yīng)的多元張量積求積公式，并在布朗片測(cè)度下計(jì)算其平均誤差.

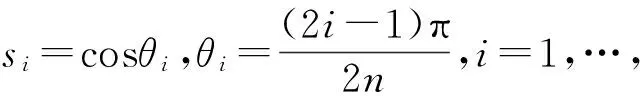
(2)

做基于T1，n的d元張量積求積公式，即對(duì)任意f∈C([-1，1]d)，

(3)

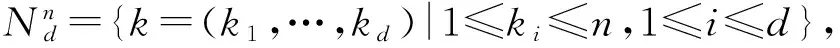
下面給出多維布朗片測(cè)度的概念.對(duì)F1={f∈C[-1，1]|f(-1)=0}賦予上確界范數(shù)，則(F1，‖·‖C)成為一個(gè)可分的Banach空間.把(F1，‖·‖C)上的Borel集記為B(F1)，B(F1)上的Wiener測(cè)度記為ω，由文獻(xiàn)[7]可知ω的協(xié)方差核為

記Fd為F1的d重張量積空間，由文獻(xiàn)[8]知Fd上的d維布朗片測(cè)度ρd的協(xié)方差核為：對(duì)任意x=(x1，…，xd)及y=(y1，…，yd)，有

(4)

2 主要結(jié)論及其證明

定理1 假設(shè)Sd(f)和Td，n(f)分別由(2)和(3)式定義，則

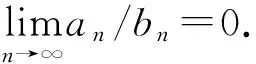
證明 由(1)―(3)式可知

(5)

其中

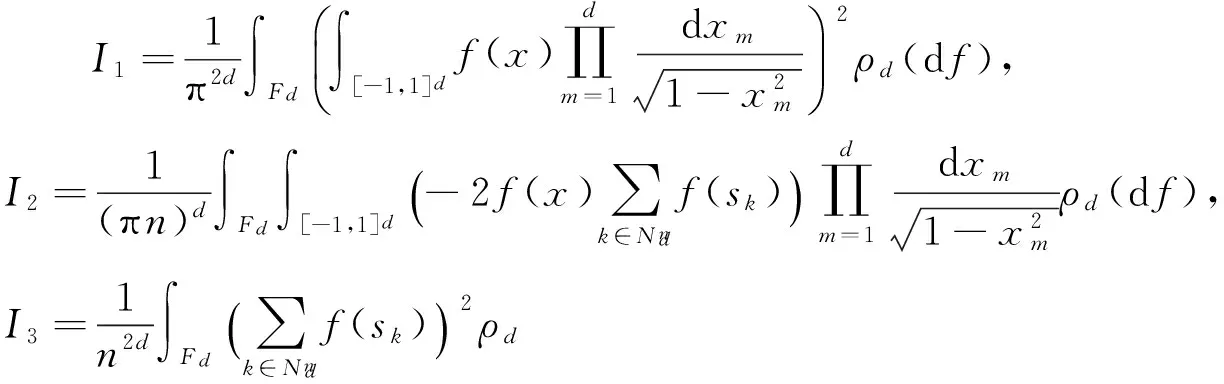
下面分別計(jì)算I1，I2，I3.對(duì)于I1，由Fubini定理及(4)式可得

(6)

(7)

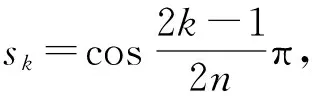
由sinx=Im(eix)，cosx=Re(eix)及等比數(shù)列求和公式得

(9)

(10)

(11)

由(7)—(11)式可得

(12)

對(duì)于I3，由(4)式可得

(13)

簡(jiǎn)單計(jì)算得

(14)

而由cosx=Re(eix)及等比數(shù)列求和公式得

(15)

由(13)—(15)式可得

(16)

由

可檢驗(yàn)得

(17)

(18)

由(5)，(6)，(12)，(16)—(18)式可得

(19)

定理證畢.

注1 目前計(jì)算多元積分的常用方法是蒙特卡洛算法和平移格算法.同這些算法相比，本文的算法為一種確定性算法，計(jì)算過程簡(jiǎn)單，而且有一定的收斂速度.特別地，當(dāng)d=1時(shí)，由文獻(xiàn)[4]知本文的算法達(dá)到了最優(yōu)逼近速度n-1.

[1] TRAUB J F，WASILKOWSKI G W，WOZNIAKOWSKI H.Information-based complexity[M].New York：Academic Press，1988：1142-1143.

[2] SULDIN A V.Wiener measure and its applications to approximation methods[J].Izv Vyssh Ucheb Zaved Mat，1959，13：145-158.

[3] SULDIN A V.Wiener measure and its applications to approximation methods[J].Izv Vyss Ucheb Zaved Mat，1960，18：165-179.

[4] KLAUS R.Average-case analysis of numerical problems[M].New York：Spring-Verlag，2000：11-225.

[5] NOVAK E，WOZNIAKOWSKI H.Tractability of multivariate problems：standard information for operator[M].Zurich：EMS，2012：99-558.

[6] RAINER K.Numerical Analysis[M].New York：Springer-Verlag，2003：72-238.

[7] XU G Q.The average errors for Lagrange interpolation on the Wiener space[J].Acta Math Sinica，2012，28：1581-1596.

[8] LIFSHITS M A.Lectures on Gaussian processes[M].New York：Springer，2012：18-117.

(責(zé)任編輯：李亞軍)

The average error of multivariate quadrature formulae on the Brownian sheet measure

DONG Yan-qi，XU Gui-qiao

(College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China)

The average errors of multivariate tensor product quadrature formulae based on the Chebyshev nodes on the Brownian sheet measure are studied and the corresponding stronger asymptotic order is obtained.In the past，the average error analysis of multivariate quadrature formula is non-constructive.But the algorithm of this paper is constructive，which is simpler and more applicable.At the same time，this algorithm has a certain convergence rate.

Chebyshev nodes；Brownian sheet measure；average error；multivariate quadrature formulae

1000-1832(2017)02-0030-04

10.16163/j.cnki.22-1123/n.2017.02.007

2015-12-12

國(guó)家自然科學(xué)基金資助項(xiàng)目(11471043).

董彥琦(1993—)，女，碩士，主要從事函數(shù)逼近論研究；通信作者：許貴橋(1963—)，男，教授，主要從事函數(shù)逼近論研究.

O 174.41 [學(xué)科代碼] 110·4140

A