基于微帶線的相位補償方法分析

徐 晟， 李心潔， 李雪珺

(1.上海無線電設備研究所， 上海 200090；2.空軍駐上海航天局軍事代表室， 上海 200090)

基于微帶線的相位補償方法分析

徐 晟1， 李心潔2， 李雪珺1

(1.上海無線電設備研究所， 上海 200090；2.空軍駐上海航天局軍事代表室， 上海 200090)

通過引入金絲鍵合線等效模型，建立微帶線旁邊增加片式電容并用金絲鍵合線互連后的相位補償電路物理模型。提取金絲鍵合線的并聯電容、串聯電感、串聯電阻等參數，計算片式電容的容值參數，推導相位補償電路物理模型的ABCD矩陣，并轉換為[S]矩陣后，通過計算S21參數的角度值，即可得知片式電容對傳輸微波信號相位的影響。同時，通過仿真試驗，驗證了該模型建立和推導的正確性。

相位補償； 金絲鍵合線； 等效模型

0 引言

由于現在雷達系統復雜性的提高，雷達系統的回波信號經過天線后，經常需要多路接收通道同時傳送。但是通道間的固有差異，使得各路接收通道的信號輸出相位存在不一致性。為此，需要對相位進行補償，以消除通道固有差異對相位的影響。

通常的相位補償方法是在微波電路中傳輸微波信號的微帶線側面增加一片覆銅層，該覆銅層作為一個片式電容與微帶線間用金絲鍵合線互連，以改變微波電路中傳輸微波信號的相位。但是該覆銅層尺寸和到微帶線距離對微波信號傳輸相位的影響都是由經驗獲得，再在電路中加以調試實現。

本文通過引入金絲鍵合線等效電路模型，理論推導片式電容經金絲鍵合線接入微帶線后，對整個微波電路相位的影響，并建立仿真模型進行驗證。結果表明，理論推導與仿真結果相一致，為微波電路中相位補償調整提供了理論設計依據。

1 金絲鍵合線等效模型

1.1 等效模型

微帶線之間金絲鍵合線互連示意圖，如圖1所示。

基于微帶線的金絲鍵合線等效模型由與兩邊微帶線并聯的電容Ce、串聯電感Lb、串聯電阻Rb等組成，如圖2所示[1-3]。

1.2 模型參數計算

對自由空間中長度為l，直徑為d的圓形金絲鍵合線，其電感Lb可表示為

(1)

式中：μ0為真空磁導率(μ0=4π×10-7H/m);μr為鍵合線的相對磁導率(對于金絲，μr=1)；δ為鍵合線的趨膚深度。

趨膚深度δ的表達式為

(2)

式中：σ為鍵合線的電導率，對于金絲，σ=4.098×107s/m；f為鍵合線傳輸信號的頻率。

串聯電阻Rb的計算公式為

(3)

式中：ρ為金絲鍵合線的電阻率。

并聯電容Ce表示為

(4)

(5)

(6)

(7)

其中：

(8)

式中：h為微帶線基片厚度；W為微帶線導帶的寬度；εr為基片的相對介電常數。

2 相位補償電路推導

基于微帶線的相位補償電路是由傳輸信號的微帶線[4]、微帶線旁的片式電容和金絲鍵合線組成，結構示意圖如圖3所示，物理模型如圖4所示。

在圖4中，θ1是信號輸入端至金絲鍵合處的微帶線的電長度，表示為θ1=2πl1/λg，λg是微波信號在微帶線上的傳輸波長，計算公式見式(6)。同樣，θ2是金絲鍵合處至信號輸出端的微帶線的電長度。Cp為片式電容，其電容值計算公式表示為

(9)

式中：ε0為真空介電常數(ε0=1/36π × 10-9F/m)；A為片式電容單極面積。

由金絲鍵合線和片式電容組成的并聯支節，在電路中作為并聯導納，表示為

(10)

其中：

因此，圖4中從信號輸入至信號輸出級聯網絡的歸一化ABCD矩陣如下表示[5]：

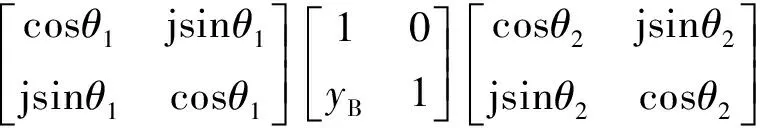
(11)

式中：yB=YB/Y0，Y0為微帶線的特性導納。

(12)

根據矩陣[a]至矩陣[S]的轉換公式(12)將式(11)轉化為矩陣[S]，計算參數S21的角度值為Angp1，即為引入片式電容后微波信號從輸入端傳至輸出端的相位延遲值。

在不引入片式電容的情況下，計算微波信號在相同微帶線上傳輸的相位延遲值為

(13)

因此，計算(Angp1-Angp0)即為片式電容引入的相位補償值。

同理，當一個片式電容不足以對所需相位進行補償時，可以引入兩個片式電容，其物理模型如圖5所示。

計算其歸一化ABCD矩陣為

(14)

根據轉換式(12)，將矩陣[aT2]轉換為矩陣[S]，得出參數S21的角度值，與微帶線本身的相位延遲作比較，算出相位補償值。

3 理論推導與仿真試驗比對

通過建立仿真模型對理論推導進行驗證，仿真模型示意如圖6所示。圖中，微帶線基片厚度h=0.127 mm；相對介電常數εr=2.2；特性阻抗Z0=50 Ω；鍵合金絲長度l=800 μm；直徑d=25 μm；片式電容尺寸為0.3 mm×0.3 mm。若工作頻率為20 GHz，微帶線總長度為3倍λ/4，兩個片式電容間隔λ/4。

由理論推導和仿真試驗得出的輸入端與輸出端相位延遲比較如表1所示。從中看出，插入1個或2個片式電容時，理論推導算得的相位補償分別為6.5°、13.1°，仿真試驗得出相位補償分別為6.8°、14.0°，理論推導的數據與仿真試驗的數據一致性很好。

表1 理論推導和仿真試驗數據比對

通過進一步的分析計算，可以得出以下結論：多個片式電容間隔無需滿足1/4波長要求；片式電容位置不能離微帶線太遠，否則過長的金絲鍵合線會增加鏈路的插損，特別在工作頻率提高后。

4 結論

本文通過引入金絲鍵合線等效模型，建立由微帶線旁邊增加片式電容并用金絲鍵合線互連后的物理模型，將該模型轉換為矩陣[S]后，計算增加片式電容對傳輸微波信號的相位影響。同時，通過仿真試驗，驗證了該模型建立和推導的正確性。因為可以方便地在微帶線旁邊增加片式電容，所以本文的分析對微波鏈路中靈活的相位補償具有參考作用。

[1] 嚴偉， 符鵬， 洪偉. LTCC微波多芯片組件中鍵合互連的微波特性[J]. 微波學報， 2003， 19(3)： 30-34.

[2] 曾耿華，唐高弟. 微波多芯片組件中鍵合線的參數提取和優化[J]. 信息與電子工程， 2007， 5(1)： 40-43.

[3] 李成國，牟善祥，張忠傳，等. 基于LTCC技術的毫米波鍵合金絲的分析與優化設計[J]. 電子器件， 2007， 30(6)： 2192-2196.

[4] 清華大學《微帶電路》編寫組. 微帶電路[M]. 北京：人民郵電出版社， 1976： 1-30.

[5] Reinhold Ludwig(著),王子宇，等(譯). 射頻電路設計——理論與應用[M]. 北京：電子工業出版社， 2002： 94-129.

Method Analysis of Phase Compensation Based on Microstrip Line

XUSheng1，LIXin-jie2，LIXue-jun1

(1. Shanghai Radio Equipment Research Institute, Shanghai 200090, China；2. The Air Force of Military Representative Office in SAST, Shanghai 200090, China)

The physical model of phase compensation is formed of microstrip line, bonding interconnection wire and chip capacitance. And the equivalent model of bonding interconnection wire consists of the parameters of shunt capacitor, series inductance, series resistor. The computing formulas of these parameters and chip capacitance is provided. Based on these formulas, the ABCD matrix of physical model of phase compensation is deduced. And then the ABCD matrix transforms [S] matrix. Through the parameter ofS21, the phase compensation of chip capacitance will be known. At last, simulation experiment verifies the validity of the deduction.

phase compensation; bonding interconnection wire; equivalent model

1671-0576(2017)01-0021-03

2016-10-12

徐 晟(1980-)，男，碩士，工程師，主要從事射頻微波電路設計。

TN830.2

A