擴頻信號的一種快速捕獲技術

董國英， 李名祺

(上海無線電設備研究所， 上海 200090)

擴頻信號的一種快速捕獲技術

董國英， 李名祺

(上海無線電設備研究所， 上海 200090)

介紹了一種雙頻域并行捕獲算法及其快速實現方法，該方法通過將時域的相關運算轉換成頻域傅里葉變換的乘法運算實現碼相位的并行搜索，且基于頻域圓周移位的原理，通過對傅里葉變換序列進行循環移位實現多普勒頻率的并行搜索，大大減小了運算量和捕獲時間。和其他算法相比，本算法捕獲時間能縮小一個數量級，尤其適于寬范圍高動態擴頻信號的快速捕獲。

碼相位； 多普勒頻率； 并行搜索

0 引言

擴頻通信具有保密性好、抗干擾能力強等諸多優點，被廣泛應用于天基測控等領域。在這種環境中，高、低軌道飛行器之間往往具有很高的相對速度和加速度，且載頻較高，會產生較大的多普勒頻移和多普勒頻率變化率，因此接收設備必須在寬范圍高動態條件下快速完成信號的捕獲，也就是必須在較短時間內完成對碼相位和載波頻率的二維搜索，而傳統的捕獲算法很可能跟不上載波頻率變化的速度。

本文介紹一種雙頻域并行快速捕獲算法，此算法將碼相位搜索變換到頻域并行實現，并基于頻域的圓周移位原理同時實現頻率的并行搜索，在資源消耗基本相當的情況下大大縮短捕獲時間，可以滿足寬范圍高動態環境下信號的快速捕獲要求。

1 常規單頻域并行捕獲算法

頻域并行碼相位搜索法將時域的相關運算變換成頻域的乘法運算[1-3]，即分別將基帶信號和本地擴頻碼序列進行FFT運算并將FFT的結果進行共軛相乘，最后將乘積進行IFFT運算，即可一次性完成所有碼相位的搜索，但是頻率維仍然需要串行搜索，在高動態環境下，多普勒范圍較寬以±90 kHz為例，如果搜索步長設置為1 kHz，則需要180次串行頻率搜索才能完成頻率維的捕獲。因此，在高動態信號環境下，多普勒頻偏范圍較寬，需要的搜索時間也會變長。

頻域并行頻率FFT搜索法將本地擴頻碼序列與接收信號進行分段相關計算[4-5]，再將各段的相關值進行FFT計算，找出FFT結果的峰值并計算對應的頻率，即可一次性完成頻率的并行搜索，但是該算法需要串行搜索所有的碼相位。對應擴頻序列的每一個碼相位都需要進行分段相關和FFT計算，遍歷所有的碼相位才能完成碼相位的捕獲。

該算法在擴頻序列較長的情況下仍需要很多次運算才能完成，比如擴頻序列長度是1023，采用2倍采樣時需要進行2046次碼相位的搜索， 搜索時間較長，不能滿足快速捕獲的要求。

2 雙頻域并行快速捕獲技術

2.1 基于快速傅里葉變換的頻域并行碼相位搜索

碼相位搜索是通過將接收信號序列x(n)和本地擴頻碼序列c(n)進行相關運算并搜索相關峰值來計算碼位移的[6]，而兩組序列在時間域內的相關運算可以通過序列x(n)和反轉序列c(-n)的線性卷積實現。

根據線性卷積的原理，將兩個序列分別進行補零，則原序列的線性卷積就等于補零后序列的循環卷積，而根據循環卷積的特性，時域的循環卷積等價于頻域的相乘，進而可以利用頻域的傅里葉變換計算時域的相關值，如下式所示

=x′(n)*c′(-n)

=IFFT{FFT[x′(n)]×FFT*[c′(n)]}

R(k) =X(k)×C*(k)

=FFT[x′(n)]×FFT*[c′(n)]

(1)

式中：L為采樣點數；*為卷積運算；FFT代表傅里葉正變換；IFFT代表傅里葉反變換；*代表求共軛；m代表碼位移；x′(n)和c′(-n)分別為x(n)和c(-n)補零后的序列。

由上式可知，實際中可以將時域的相關轉換到頻域上完成，只需將接收基帶信號進行FFT計算，同時將產生的本地碼序列進行FFT計算，兩個序列的FFT結果進行共軛相乘，并將乘積進行IFFT計算，即得到兩個序列在所有相位上的相關值，對相關峰值進行檢測，即可一次性搜索所有碼相位，實現碼相位的并行搜索。

2.2 基于頻域圓周移位的并行多普勒頻率搜索

由傅里葉變換的圓周頻域移位特性可知，對N點的DFT如果[7]

(2)

那么

(3)

因此，序列x(n)與復指數序列ej2πln/N的乘積的傅里葉變換等于X(k)在圓周頻域移位l個單位，記為x((k-l))N。

因此，將傅里葉變換序列X(k)循環移動l位再與C*(k)相乘并做IFFT:

(4)

即對傅里葉變換序列X(k)進行循環移位與在時域內對x(n)進行頻率補償后再做FFT等效[8]，因此做一次FFT計算并通過FFT結果的頻域圓周移位即可同時完成頻率和碼相位的并行搜索，算法計算量大大減小。

通過對X(k)進行不同位移的移位后與C*(k)相乘并做IFFT，找出IFFT結果組內模值的最大值，并最終找出組間的最大值，通過其對應的組位移計算多普勒頻移，通過IFFT模值最大值的位置計算碼相位。捕獲的原理框圖如圖1所示。

從上圖可以看出，通過將時域相關變換到頻域兩個序列FFT的乘積，再進行IFFT計算，完成并行碼相位搜索；同時基于頻域圓周移位將信號FFT進行循環移位后，再與碼序列的FFT相乘，并將乘積進行IFFT計算，完成并行多普勒頻移搜索。這樣雙頻域快速捕獲算法同時在頻域完成了對碼相位和多普勒頻率的二維搜索，運算量和捕獲時間都顯著減小。

2.3 雙頻域捕獲算法的快速實現方法

對一個偽碼周期時間內的接收基帶信號做N點FFT，并將其結果存儲在RAM中，這樣頻域的循環移位就可以通過控制讀取存儲單元的順序實現，并且通過RAM的緩存作用，處理時鐘不再受到采樣率的限制，可以采用比較高的時鐘域進行乘法和IFFT計算，從而減小捕獲時間。基于FPGA平臺采用流水線的形式進行乘法和IFFT計算，可實現快速處理。

首先將兩個序列的FFT結果分別存儲在不同的RAM中，然后分別連續讀取RAM多次(需要連續讀取RAM的次數為多普勒頻偏范圍除以FFT頻率精度的商，假設為m次)。對存儲基帶信號FFT結果的RAM每次重新讀取都較上一次有1個地址偏移，以此實現頻域的圓周移位，而存儲本地碼序列FFT結果的RAM只需順序讀取即可。將讀出的兩個序列進行共軛相乘，并對乘積進行IFFT計算，IFFT的計算結果可分為m組，分別對應頻域m點循環移位的相關值，即分別對應頻域的m次搜索。從每組結果中找出模值的最大值和對應位置，并最終找出組間最大值。最大值所在的組序號乘以fs/N(fs為基帶信號采樣率，N為FFT點數)即為多普勒頻偏，而其對應的位置即為碼相位偏移。

本方法通過RAM的緩存作用，將所有的乘法和IFFT計算都放在高時鐘域進行，并以流水線的形式實現頻域的多次搜索，大大減小了捕獲時間。

3 捕獲性能分析

設定頻率捕獲范圍是±100 kHz，擴頻碼長度是1 023，擴頻碼速率是10.23 Mcps，數據速率是8 kbps，采樣率是20.46 MHz，高速主處理時鐘為120 MHz。為了防止比特跳變的影響，取2個比特時間內的接收信號數據和1個比特時間內的碼序列進行計算，其采樣點數分別是5 115個點和2 558個點，分別補零到8192點做8192點的FFT。采樣率是20.46 MHz，做8192點的FFT，可以得出FFT頻率精度是2 497.6 Hz，則±100 kHz的多普勒范圍需要搜索81次。

下面將頻域并行碼相位搜索法、頻域并行頻率FFT搜索法以及雙頻域并行捕獲方法三種方法的計算量和捕獲時間分別進行比較。

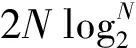
對雙頻域并行捕獲算法來說，主要包括以下計算：

b) 將信號FFT與本地碼的FFT共軛相乘需實數乘法4N次；

d) 基于頻域圓周移位將信號FFT結果進行循環移位然后重復b)、c)搜索81次，因而共需實數乘法20 119 552次，實數加法26 198 016次。

頻域并行碼相位搜索法和雙頻域并行捕獲方法相比只有d)不同，需將本地載波NCO修正一個步長后進行混頻，然后重復a)～c)81次(頻率精度相同條件下)，則共需實數乘法37 158 912次，實數加法51 757 056次。

頻域并行頻率FFT搜索法每個碼相位需要做一次5 115點的相關累加和一次FFT(以128個分段即128點FFT為例)，共需要搜索2 046個碼相位，共需實數乘法45 527 592次，實數加法26 430 228次。

雙頻域并行捕獲算法的快速實現方法采用流水線的方式實現頻域的圓周移位，供需進行1次FFT計算和81次IFFT計算，按照主處理時鐘是120 MHz，流水線運算的(乘積及IFFT)的處理時間為5.6 ms；比較而言，頻域并行碼相位搜索法運算需要進行81次FFT計算和81次IFFT計算，處理時間為11.35 ms；頻域并行頻率FFT搜索法需要進行2 046次5 115點的相關運算和128點的FFT運算，處理時間為87.2 ms。需要特別說明的是，上面只計算了數學運算的處理時間，且所有的運算均在高時鐘域進行，而捕獲時間除了運算時間外還應包括FFT運算的處理時延，即從FFT輸入使能拉高到FFT輸出使能拉高之間的時間(一般小于200 μs)。

從表1可以看出，和頻域并行碼相位搜索法相比，本算法加法和乘法運算次數分別減小了50%和46%，運算時間減小了一半；和頻域并行頻率FFT搜索法相比，本算法加法運算次數相當，乘法運算次數減小了56%，而運算時間更是小了一個數量級，因此雙頻域并行捕獲算法運算量小，捕獲時間短，比較適合高動態環境的快速捕獲。

表1 運算量和運算時間比較

4 結論

本算法通過將兩個序列的時域相關運算轉換到頻域傅里葉變換的乘法運算，并對乘積進行傅里葉逆變換，實現頻域碼相位的并行搜索，并基于頻域圓周移位的原理，依次將接收信號的傅里葉變換序列進行圓周移位后再進行乘法和傅里葉逆變換，實現頻域多普勒頻率的搜索。和頻域并行碼相位搜索法相比，本算法可以在消耗資源不變且捕獲靈敏度相同的情況下，節省一半的運算量和捕獲時間，和其他捕獲算法相比，本算法最大的優勢就是捕獲時間短，可以將捕獲時間縮小一個數量級，因此特別適用于擴頻信號的快速捕獲。

[1] 張帆. GPS捕獲設計與VLSI實現方法[D].西安：西安電子科技大學, 2011: 15-26.

[2] 祁東杰. 大頻偏-高動態擴頻信號捕獲跟蹤技術及其FPGA實現[D]. 北京：北京理工大學, 2015: 14-28.

[3] 趙春燕， 崔嵬. 一種可克服非相干數據影響的直擴信號捕獲算法[J]. 電子學報, 2011, 39(7): 1491-1496.

[4] 謝偉. GPS中偽隨機碼的捕獲技術研究[D]. 安徽：安徽大學, 2007: 26-46.

[5] 黃振, 陸建華,楊士中. 基于 DMF 直擴系統捕獲性能的研[J]. 電路與系統學報, 2002, 7(1): 92-95.

[6] 梁麗芳. 基于FPGAt利用FFT算法實現GPSC-A碼捕獲的研究[D].遼寧：大連海事大學, 2009: 14-23.

[7] 方艷梅，劉永清，等(譯). 數字信號處理—原理、算法與應用[M]. 北京：電子工業出版社, 2014: 350-356.

[8] 張現宇，郭熙業，王躍科，等. 一種高動態環境下衛星擴頻信號的快速捕獲方法研究[J]. 宇航計測技術, 2014, 34(4): 18-22.

Quickly Acquisition Technology of Spread Spectrum Signals

DONGGuo-ying,LIMing-qi

(Shanghai Radio Equipment Research Institude, Shanghai 200090, China)

An bi-frequency domain acquisition algorithm and its fast implementation method is given, which can realize the search of code phase and Doppler frequency in parallel. Instead of calculating correlation in time domain, the parallel search of code phase is carried out by executing multiplication in frequency domain. Meanwhile，based on the principle of circular shift of frequency domain, the fourier transform sequence is cyclic shifted with different offset to search Doppler frequency in parallel. As a result, the amount of computation and the capture time is significantly reduced. Compared with other algorithms, the capture time can be reduced greatly. So it is suitable for rapid acquisition of spread spectrum signals under large deviation and high dynamic conditions.

code phase; Doppler frequency; parallel search

1671-0576(2017)01-0048-04

2016-12-16

董國英(1984-)，女，工程師，碩士，主要從事彈載數據鏈方向的基帶信號處理研究工作；李名祺(1986-)，男，工程師，碩士，主要從事授時通信、彈載數據鏈等信號處理方面的研究工作。

TN914.42

A