GPS衛星和接收機天線絕對PCO、PCV對高精度基線解算的影響分析

胡一帆，胡 弦，陳俊平，胡叢瑋

(1. 中國科學院上海天文臺，上海 200030； 2. 同濟大學測繪與地理信息學院，上海 200092；3. 武漢大學GNSS中心，湖北 武漢 430079)

GPS衛星和接收機天線絕對PCO、PCV對高精度基線解算的影響分析

胡一帆1，2，胡 弦3，陳俊平1，胡叢瑋2

(1. 中國科學院上海天文臺，上海 200030； 2. 同濟大學測繪與地理信息學院，上海 200092；3. 武漢大學GNSS中心，湖北 武漢 430079)

在高精度GPS衛星導航數據處理中，衛星和接收機天線的PCO和PCV作為重要的誤差來源之一，必須予以改正。本文從高精度基線解算入手，分析了衛星和接收機天線PCO和PCV中各項對高精度基線解算結果的影響。試驗結果表明，接收機天線PCO、PCV對長基線或超長基線在各分量方向或長度上的影響最大可達到101 mm。衛星天線PCO、PCV對長基線在各分量方向或長度上的影響在毫米水平，最大不超過4 mm；對超長基線在各分量方向或長度上的影響最大可達到40 mm。

衛星天線；接收機天線；絕對PCO、PCV；高精度基線解算

高精度GPS測量中，天線相位中心的偏差和天線相位中心變化是一項重要的誤差源，其對高程分量的影響最為顯著[1]。自1996年6月30日起，IGS的各數據分析中心開始利用相對相位中心的改正模型來改正這一誤差項。相對相位中心改正的前提是假定參考天線(AOAD/M_T型天線)的PCV為0。但實際上AOAD/M_T型天線的PCV并不為0，再加上低高度角時通過相對校驗方式得到的天線的PCV值所受到的多徑影響將顯著增加等一系列缺點[2]，2006年11月后，IGS提供的天線產品均基于絕對相位中心改正模型的結果。此外，絕對天線相位中心改正模型除了考慮接收機天線相位中心的改正外，還給出了GPS衛星的天線相位中心的改正，以減小基于長基線測定的GPS全球參考框架與使用其他觀測技術(VLBI和SLR)得到的結果間的尺度誤差[3-8]。

1 接收機天線相位中心改正

對接收機而言，天線信號的相位中心不是固定的，而是隨著衛星信號的入射方向變化的。天線瞬時相位中心偏差主要依賴于衛星的高度角和方位角。接收機天線類型決定了天線接收到的不同方向衛星信號相位中心的坐標。平均相位中心是不同方向衛星信號相位中心的加權平均值。平均相位中心和天線參考點所形成的向量即為天線相位中心偏差(PCO)。如圖1所示，天線相位中心偏差為Xoff。第2個接收機天線誤差項為該接收機對衛星信號的瞬時相位中心和平均相位中心的偏差(PCV)，該偏差為衛星高度角e和方位角α的函數[4]，表示為ΔφPCV(α，e)。

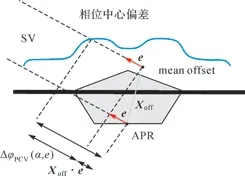
圖1 接收機天線改正模型

由圖1可知，接收機對于高度角為e、方位角為α的衛星的相位觀測值的接收機天線改正項為Δεφ(α，e)，其計算公式如下

Δεφ(α,e)=ΔφPCV(α,e)+Xoff×e(α，e)

(1)

式中，e(α，e)為觀測方向單位向量。

2 衛星天線相位中心改正

衛星天線相位中心偏差(PCO)和天線相位中心變化(PCV)通常是在星固系下定義的。

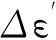
(2)

式中，z′為低點角，其計算公式如下

(3)

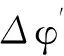
3 算例分析

在基線長度較短(小于50 km)時，基線兩端點GPS接收機對同一共視衛星的高度角和方位角基本一致，在形成站間單差觀測值時，衛星天線的PCO和PCV改正將會被抵消掉。因此，本文主要選取長基線(100～1000 km)和超長基線(大于1000 km)來進行相關分析。

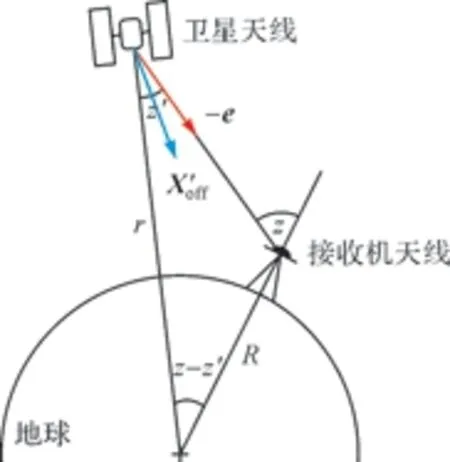
圖2 衛星天線改正模型

選取美國南加州的7個IGS觀測站來組成長基線(測站分布如圖3所示)，選取亞太地區的6個IGS觀測站來組成超長基線，剔除部分長度超過5000 km的基線，最后形成的觀測基線如圖4所示。取2016年年積日159—165的一周觀測數據進行高精度基線解算[9-11]。

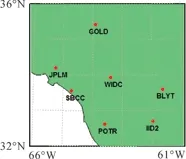
圖3 測站南加州分布

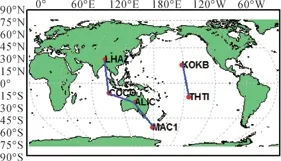
圖4 亞太地區測站分布

3.1 改正衛星天線PCO、PCV和接收機天線PCV的基線解算結果

測站天線PCO改正的計算公式如下

(4)

式中，rec_corr為測站地平坐標系中由測站接收機天線PCO引起的測站坐標改正量向量；f1表示L1頻率；f2表示L2頻率；PCOL1、PCOL2分別表示接收機天線L1、L2頻率上的PCO。由測站天線PCO可得到測站天線PCO對測站坐標的改正量[12-16]，見表1。

表1 測站天線PCO對測站坐標的改正量 mm

由表1可知，在忽略N、E方向的測站坐標改正量的情況下，長基線BLYT、GOLD、IID2、JPLM、POTR、SBCC測站U方向坐標改正量均在35～50 mm之間，而WIDC測站U方向坐標改正量為80.7 mm；超長基線ALIC、LHAZ測站U方向坐標改正量在165～170 mm之間，COCO、KOKB、MAC1、THTI測站U方向坐標改正量在47 mm左右。將對衛星天線PCO、PCV和接收機天線PCO、PCV進行改正的基線解算結果與對衛星天線PCO、PCV和接收機天線PCV進行改正的基線解算結果作差，其結果見表2。

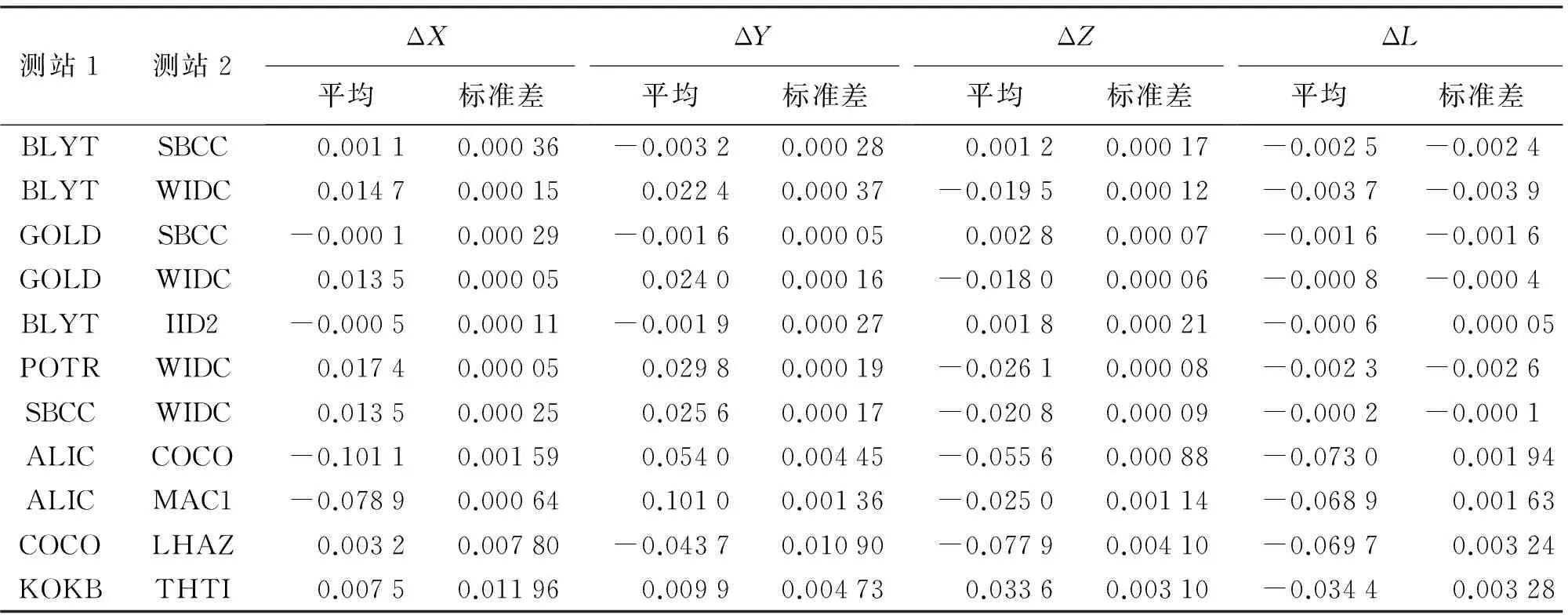
表2 無接收機天線PCO改正的部分基線結果偏差 m

由表2可知，ΔX、ΔY、ΔZ、ΔL的標準差對于長基線均小于0.4 mm，對于超長基線均在毫米級，少數幾個達到厘米級但小于2 cm，說明連續單天解基線各分量差值非常穩定，可由ΔX、ΔY、ΔZ、ΔL多天的均值來分析差值的性質。測站天線PCO對長基線各分量的影響能達到厘米級，對超長基線各分量的影響能達到十幾厘米。如果構成基線的兩測站U方向坐標改正量相近，則基線各分量的偏差較小，長基線中的BLYT—SBCC、GOLD—SBCC、BLYT—IID2基線各分量偏差均小于3.2 mm。兩測站U方向坐標改正量相差較大時，如POTR—WIDC各分量偏差可達3 cm；超長基線中的KOKB—THTI基線各分量偏差均小于3.3 cm，兩測站U方向坐標改正量相差較大時，如COCO—LHAZ各分量偏差可達11 cm。

此外，表2中ΔL均為負，說明未改正測站PCO基線長度會系統性地增加。在基線的兩測站U方向坐標改正量相近的情況下，測站PCO影響如圖5所示。

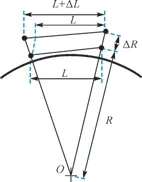
圖5 測站PCO影響示意圖

由圖5可得

(6)

式中，L+ΔL為測站的天線相位中心移動后所形成的基線長度；L為原來的基線長度；R+ΔR為測站的天線相位中心移動后天線相位中心到地心的距離；ΔR測站的天線相位中心移動的距離。當ΔR值取40 mm、R值取6378 km、基線長度在300 km左右時，ΔL為-2 mm；當基線長度在4000 km時，ΔL為-32 mm。ΔL=-2 mm與表1中不包含WIDC的長基線的ΔL值基本相符；ΔL=-32 mm與表1中超長基線KOKB—THTI的ΔL值基本相符。

3.2 改正衛星天線PCO、PCV和接收機天線PCO的基線解算結果

將對衛星天線PCO、PCV和接收機天線PCO、PCV進行改正的基線解算結果與對衛星天線PCO、PCV和接收機天線PCO進行改正的基線解算結果作差，結果見表3。

由表3可知，對于長基線ΔL最大不超過2.5 mm，但是包含測站WIDC的基線，基線分量偏差ΔX、ΔY、ΔZ能達到厘米級，最大可達到3.2 cm，其他長基線的基線分量偏差ΔX、ΔY、ΔZ均在毫米級。這是因為BLYT、GOLD、IID2、JPLM、POTR、SBCC測站天線PCV參數相近，而WIDC測站天線PCV參數與其他測站天線PCV參數差異較大。圖6展示了GOLD、POTR和WIDC 3個測站天線PCV，可明顯看出WIDC測站天線PCV在L1上與GOLD和POTR天線的差異。

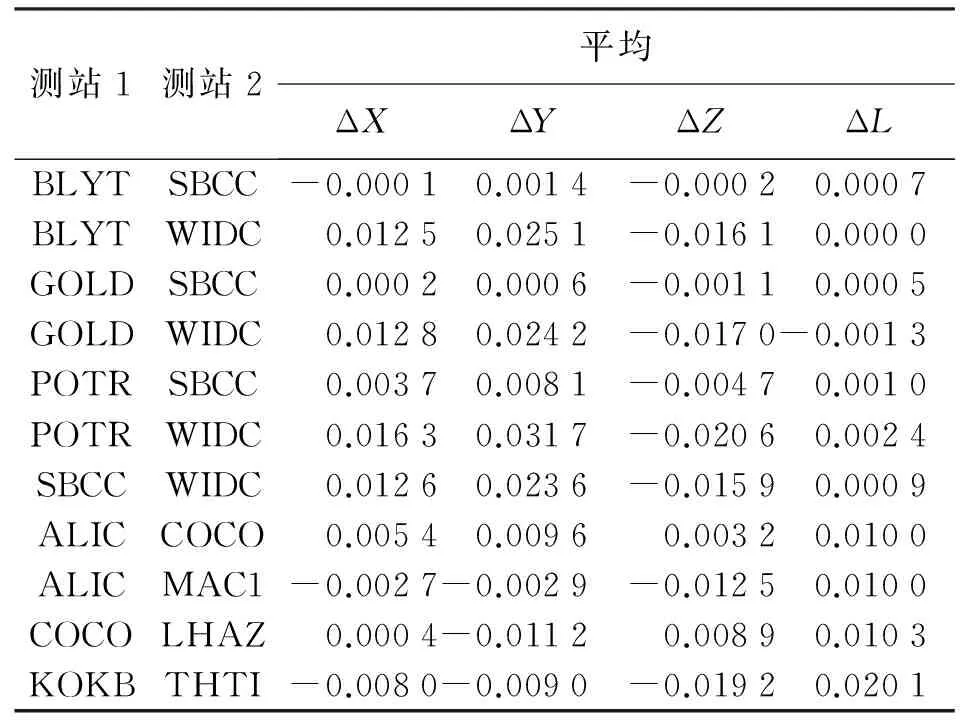
表3 無接收機天線PCV改正的部分基線結果偏差 mm

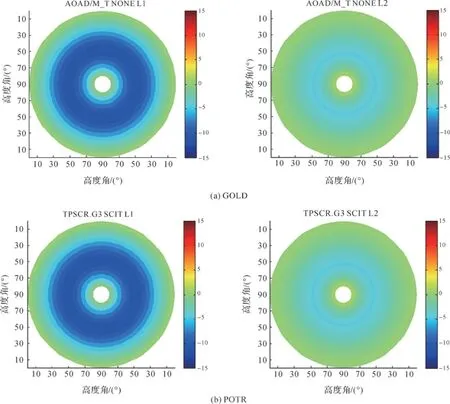
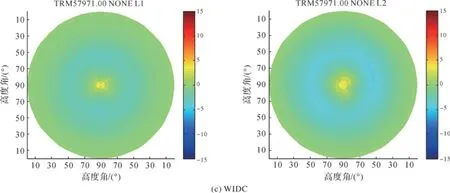
圖6 GOLD、POTR、WIDC測站PCV

由表3可知，對于超長基線的影響不管是基線分量偏差ΔX、ΔY、ΔZ還是基線長度偏差ΔL，均能達到厘米級，最大可達到1.9 cm。雖然ALIC和LHAZ兩測站天線PCV參數相近，COCO、KOKB、MAC1、THTI 4測站天線PCV參數相近，但是基線KOKB-MAC1在ΔZ和ΔL上均存在2 cm左右的偏差。這是因為基線長度在300 km左右時，基線兩端測站觀測到的同一個衛星的高度角和方位角大小相近；在測站天線PCV又相近的情況下，在組成差分觀測值時能正好將測站天線PCV改正項抵消掉，而測站天線PCV差異較大時則不能抵消掉；然而在基線長度大于2000 km左右時，基線兩端測站觀測到的同一個衛星的高度角和方位角大小差異已經很大，不管基線兩端點測站天線PCV相同與否，在組成差分觀測值時測站天線PCV改正項都無法抵消掉。

3.3 改正衛星天線PCV和接收機天線PCO、PCV的基線解算結果

將對衛星天線PCO、PCV和接收機天線PCO、PCV進行改正的基線解算結果與對衛星天線PCV和接收機天線PCO、PCV進行改正的基線解算結果作差，結果見表4。

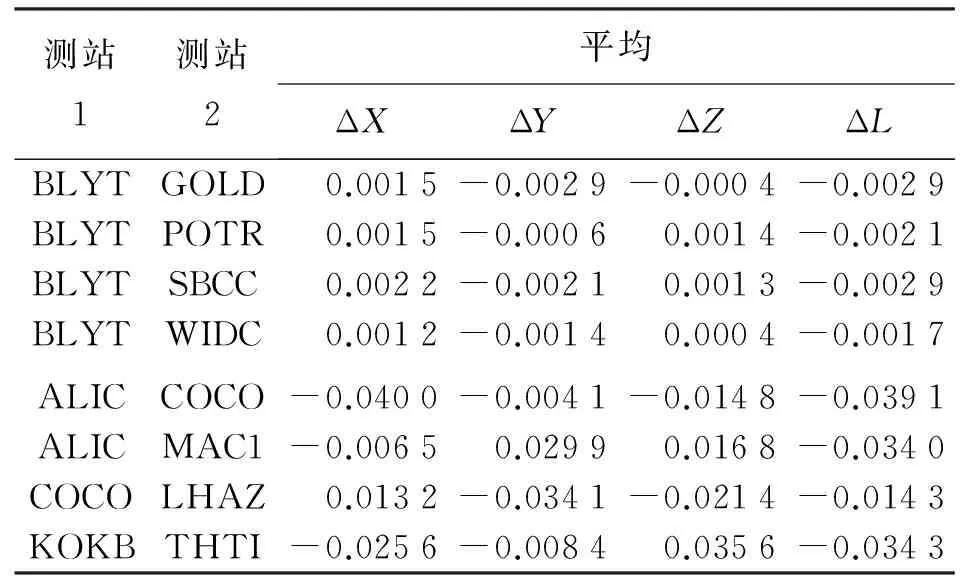
表4 無衛星PCO改正的部分基線結果偏差 m

由表4可知，衛星天線PCV對長基線的影響不管是基線分量偏差ΔX、ΔY、ΔZ還是基線長度偏差ΔL均在毫米級，最大不超過4 mm；對超長基線的影響不管是基線分量偏差ΔX、ΔY、ΔZ還是基線長度偏差ΔL均在厘米，最大能達到4 cm。造成這種差異的原因是基線長度在300 km左右時，由同一個衛星觀察基線兩端測站的低點角和方位角大小相近，在組成差分觀測值時能正好將衛星天線PCO改正項抵消掉；然而在基線長度大于2000 km左右時，由同一個衛星觀察基線兩端測站的低點角和方位角相差較大，在組成差分觀測值時衛星天線PCO改正項無法抵消掉。

3.4 改正衛星天線PCO和接收機天線PCO、PCV的基線解算結果

將對衛星天線PCO、PCV和接收機天線PCO、PCV進行改正的基線解算結果與對衛星天線PCO和接收機天線PCO、PCV進行改正的基線解算結果作差，結果見表5。

由表5可知，衛星天線PCV對長基線的影響不管是基線分量偏差ΔX、ΔY、ΔZ還是基線長度偏差ΔL基本在毫米以下，最大值為1 mm；對超長基線的影響不管是基線分量偏差ΔX、ΔY、ΔZ還是基線長度偏差ΔL大部分在毫米級，僅基線KOKB—THTI在X方向達到2 cm。這是因為基線長度在300 km左右時，由同一個衛星觀察基線兩端測站的低點角和方位角大小相近，在組成差分觀測值時能正好將衛星天線PCV改正項抵消掉；然而在基線長度大于2000 km左右時，由同一個衛星觀察基線兩端測站的低點角和方位角相差較大，在組成差分觀測值時衛星天線PCV改正項無法抵消掉。

綜上分析，衛星天線PCO、PCV和接收機天線PCO、PCV對高精度基線解算的影響見表6。

表6 接收機和衛星天線PCO、PCV各項對基線解算結果的影響

改正項長基線超長基線ΔXYZΔLΔXYZΔL接收機天線PCO0～58mm<4mm3～101mm34～73mm接收機天線PCV0～32mm<3mm0～20mm10～21mm衛星天線PCO<4mm<4mm4～36mm14～40mm衛星天線PCV<1mm<1mm0～20mm7～10mm

4 結 語

綜上可知，接收機天線PCO、PCV對長基線解算，在基線各分量上的影響可達到厘米，對基線長度的影響小于4 mm，對超長基線解算，在基線各分量上的影響在厘米水平，最大可達到10 cm，對基線長度的影響在厘米水平；衛星天線PCO、PCV對于長基線解算，在各分量和長度上的影響均在毫米水平，其中衛星天線PCV的影響基本可以忽略不計，但是對于超長基線解算，在各分量和長度上的影響均可達到厘米。此外，對于長基線，當基線兩端測站接收機天線PCO對測站坐標U方向的改正量相近時，測站天線PCO的影響不會很好地反映出來，當基線兩端測站接收機天線PCV相近時，測站天線PCV的影響也不會很好地反映出來，此時可以通過僅改正基線兩端測站中的一個測站將該影響體現出來。

[1] 朱智勤, 李征航, 劉萬科. 相位中心改正模式的轉變對GPS數據處理的影響[J]. 武漢大學學報(信息科學版), 2009，34(11):1301-1304.

[2] BILICH A L, MADER G L. GNSS Absolute Antenna Calibration at the National Geodetic Survey[J]. American Geophysical Union, 2009(3):308-312.

[3] SCHMID R, ROTHACHER M. Estimation of Elevation-dependent Satellite Antenna Phase Center Variations of GPS Satellites[J]. Journal of Geodesy, 2003, 77(7):440-446.

[4] WüBBENA G, SCHMITZ M, BOETTCHER G, et al. Absolute GNSS Antenna Calibration with a Robot: Repeatability of Phase Variations, Calibration of GLONASS and Determination of Carrier-to-Noise Pattern[C]∥Processing of the IGS Workshop.Darmstod:ESOC,2006.

[5] SCHMID R, ROTHACHER M, THALLER D, et al. Absolute Phase Center Corrections of Satellite and Receiver Antennas[J]. GPS Solutions, 2005, 9(4):283-293.

[6] ZHU S Y, MASSMANN F H, YU Y, et al. Satellite Antenna Phase Center Offsets and Scale Errors in GPS Solutions[J]. Journal of Geodesy, 2003, 76(11):668-672.

[7] SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a Consistent Absolute Phase-center Correction Model for GPS Receiver and Satellite Antennas[J]. Journal of Geodesy, 2007, 81(12):781-798.

[8] GE M R, GERD G. Estimation and Validation of the IGS Absolute Antenna Phase Center Variations[R].[S.l.]:IGS,1999.

[9] HERRING T A, KING R W, MCCLUSKY S C. GAMIT Reference Manual：release 10.4[M]. [S.l.]：MIT. 2010.

[10] 王堅, 高井祥, 王金嶺. 基于經驗模態分解的GPS基線解算模型[J]. 測繪學報, 2008, 37(1):10-14.

[11] 鄭作亞, 韓曉冬, 黃珹,等. GPS基線向量的非線性解算及精度分析[J]. 測繪學報, 2004, 33(1):27-32.

[12] 姚宜斌. GPS精密定位定軌后處理算法與實現[D]. 武漢：武漢大學, 2004.

[13] HU C W,CHEN W,GAO S H,et al.Data Processing for GPS Precise Point Positioning[J]. 南京航空航天大學學報(英文版), 2005, 22(2):124-131.

[14] 張小紅, 左翔, 李盼,等. BDS/GPS精密單點定位收斂時間與定位精度的比較[J]. 測繪學報, 2015, 44(3):250-256.

[15] 葉世榕. GPS非差相位精密單點定位理論與實現[D]. 武漢：武漢大學, 2002.

[16] 許長輝, 高井祥, 周鋒,等. 精密單點定位的可靠性研究[J]. 武漢大學學報(信息科學版), 2012, 37(6):709-713.

Analysis of GPS Satellite and Receiver Antenna Absolute PCO/PCV Influence on High Precise Baseline Resolution

HU Yifan1,2,HU Xian3,CHEN Junping1,HU Congwei2

(1. Shanghai Astronomical Observatory，Chinese Academy of Sciences, Shanghai 200030, China; 2. College of Surveying and GEO-Informatics,Tongji University, Shanghai 200092, China； 3. GNSS Center of Wuhan University, Wuhan 430079, China)

As one significant error source, the receiver antenna and GPS satellite antenna PCO/PCV must be corrected in high accuracy data processing. In this paper, the influence of receiver antenna and GPS satellite antenna PCO/PCV is analyzed for baseline processing. The result shows that the effects of receiver antenna PCO/PCV for long and very long baseline in components and length can reach 101 mm. The effects of satellite antenna PCO/PCV for long baseline in components and length are in millimeter level, the maximum is less than 4 mm, for very long baseline, the effects in components and length can reach 40 mm.

satellite antenna； receiver antenna； absolute PCO/PCV； baseline resolution

胡一帆，胡弦，陳俊平,等.GPS衛星和接收機天線絕對PCO、PCV對高精度基線解算的影響分析[J].測繪通報，2017(5)：11-16.

10.13474/j.cnki.11-2246.2017.0144.

2016-10-27

國家863計劃(2014AA123102)；國家自然科學基金(11273046)

胡一帆(1991—)，男，碩士生，主要研究方向為GNSS衛星導航定位。E-mail:1553055148@qq.com

P228

A

0494-0911(2017)05-0011-06