基于EEMD與Markov Chain的雷暴日動態與趨勢預測
——以鹽城地區為例

陳 超，李鵬飛，肖穩安，張春龍，呂東波

(1.江蘇省鹽城市大豐區氣象局，江蘇 鹽城 224100；2.中國氣象局 氣溶膠與云降水重點開放實驗室，江蘇 南京 210044；3.黑龍江省氣象災害防御技術中心，黑龍江 哈爾濱 150030；4.中國氣象科學研究院 高緯度雷電研究實驗室，黑龍江 哈爾濱 150030)

基于EEMD與Markov Chain的雷暴日動態與趨勢預測
——以鹽城地區為例

陳 超1,2，李鵬飛2,3,4*，肖穩安2,4，張春龍2,3,4，呂東波3,4

(1.江蘇省鹽城市大豐區氣象局，江蘇 鹽城 224100；2.中國氣象局 氣溶膠與云降水重點開放實驗室，江蘇 南京 210044；3.黑龍江省氣象災害防御技術中心，黑龍江 哈爾濱 150030；4.中國氣象科學研究院 高緯度雷電研究實驗室，黑龍江 哈爾濱 150030)

以鹽城地區為例，通過滑動t突變檢驗、EEMD(集合經驗模態分解，Ensemble Empirical Mode Decompositon)以及Markov Chain(馬爾科夫鏈)統計模型，對鹽城地區54 a年雷暴日數據進行動態與趨勢預測研究，并對周期研究結果進行顯著性和誤差檢驗，結果表明：鹽城地區54 a年雷暴日呈現減少的趨勢，突變年為1966年，其54 a年雷暴日序列可以分解成4個IMF(Intrinsic Mode Function)分量和1個趨勢分量。主要存在0～0.05、0.45～0.50 Hz兩個頻率區間，相應的其周期為2.22 a年際周期和27 a年代際周期(可信度均超過95%)。EEMD重構雷暴日數據與原始數據的誤差百分比處于±0.8%范圍內，其馬爾科夫鏈長周期預測顯示未來年雷暴日處于25～35 d之間的概率為45%，大于35 d的概率為32%。

鹽城地區；年雷暴日；EEMD；Hilbert變換；馬爾科夫鏈

近年來，全球溫度升高以及氣候變化，導致極端強對流天氣時常發生，雷電災害也愈發頻繁。由于敏感性元件在電子電器等智能電氣領域廣泛應用，導致設備的防雷電過電壓、雷電電磁脈沖等的能力降低，由雷電災害帶來的經濟損失呈現指數增長。因而探究雷暴日發生動態周期等規律受到越來越多專家學者們的關注[1-5]。

雖然近10年國內閃電定位系統發展迅速，但是由于其監測系統裝備時間較短，可供研究基礎數據的時間尺度較小等原因，并不能深度挖掘雷電較長年代際演變的規律，而年雷暴日作為衡量一個地區一年中雷電放電的天數，從建國初期就有完整的記錄，數據時間跨度較大以及累積量大。因此，以雷暴日作為研究對象進行動態與趨勢預測的統計分析，具有非常高的實用價值[6]。在對氣象數據的年際變化趨勢、周期特征、極端事件等方面的研究過程中[7-8]，小波分析法作為探究周期特征的主要手段被廣泛使用。但是，最新研究表明：小波分析的自適應性具有相當大的局限性[9]。而由Huang等專家提出的基于EEMD分解的HHT(Hilbert Huang Transform)模型，可以對非線性非平穩信號進行分析，而且其自身具有非常好的自適應性等優點，勢必逐漸替代小波分析法，成為多個領域內進行多尺度周期分析統計的主流方法。同樣，對合理分析雷暴日的多尺度周期規律，具有目前其他算法無法比擬的準確度。鹽城地區位于江蘇省東部、黃海之濱，是長江三角洲重要的區域性中心城市，也是著名的“中國麋鹿之鄉”、“中國優秀旅游城市”。本文基于滑動t突變檢驗，集合經驗模態分解-希爾伯特黃變換法以及馬爾科夫鏈模型，對鹽城地區1960～2013年共54年雷暴日序列進行動態與趨勢預測研究，為鹽城地區相關政府部門進一步制定防雷減災決策提供有力的科學參考依據。

1 方法介紹

1.1 滑動t突變檢驗法

氣候突變的主要表現是氣候數據在時空上從一個統計特性到另一統計特性的急劇變化。即從一種相對穩定的時態(或者是一種穩定趨勢持續變化)跳躍式地變化成另外一種相對穩定的時態的現象[10]。

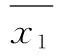
(1)

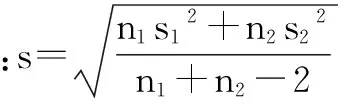
1.2HHT-EEMD法

由于HHT-Huang的核心經驗模式分解算法(EMD，EmpiricalModeDecomposition)存在一定的模態混疊問題[11-14]。即一個IMF(IntrinsicModeFunction)中包含差異極大的特征時間尺度，或者相近的特征時間尺度分布在不同的IMF中，導致相鄰的IMF波形相互混疊而難以辨認。由此可能降低Hlibert變換后結果的準確度，間接影響了多尺度分析的結果，造成多尺度周期的誤判。然而，在EMD改進的EEMD法中，核心算法是進行加入白噪聲信號[15]，驗證發現，經過添加白噪聲后的分解算法可以有效解決了EMD算法中的模態混疊問題，并且白噪聲在計算過程中將相互抵消，基本不會影響原始數據的分解。

可以將時變信號x(t)表述為：

X(t)=x(t)+ω(t)

(2)

式中：ω(t)是符合正態分布的小幅度高斯白噪聲；X(t)為疊加入白噪聲后的信號，并得到下式：

(3)

式中：ε是白噪聲幅值；N是噪聲的總數；εn是重構的信號與原始信號對比后的計算誤差值。根據式(2)，將EMD對X(t)進行分解，得到各階IMF分量，則X(t)可以表示為：

(4)

向X(t)加入符合式(3)的隨機白噪聲并重復上述過程，可得：

(5)

多次平均后，噪聲將相互抵消，而高斯白噪聲由于其零均值的特性，從而并不會影響到原信號的變化情況，則原始信號所對應的IMF分量imfn(t)為：

(6)

因此，x(t)可以分解為下式：

(7)

式中：imfn(t)為各個IMF分量；rm(t)為趨勢項，最后對各個IMF分量分別進行Hilbert變換[13]。

1.3 馬爾科夫鏈法

馬爾科夫鏈是一類特殊的馬爾科夫過程，其狀態與時間都是離散形式，其原理是基于變量的現在狀態與動向，從而對將來的狀態與動向進行預測分析。由于具有的馬爾科夫性對歷史數據的需求不多，因而可通過計算狀態轉移概率預測內部狀態的變化，適用性較好[16]。

若隨機過程{x(t),t∈T}對于任意整數和狀態a1,a2,a3,…,an∈A條件概率滿足：

(8)

其一步轉移矩陣為：

(9)

k步轉移概率可由方程p(k)=pk得到。

2 鹽城地區雷暴日數據分析

2.1 資料選取

鹽城地區1960～2013年逐月雷暴日數據來源于江蘇省氣象局資料中心。將逐月雷暴日資料整理成年雷暴日時間序列，其中最大年雷暴日為54d，發生在1964年；最小年雷暴日為13d，出現在2013年，多年平均雷暴日為33.3d。最早的初雷日發生在1996年，最晚的終雷日發生在1997年。初雷日與終雷日間天數最長為320d。

從圖1可得，鹽城地區1960～2013年的相鄰年雷暴日變化波動較強烈，相鄰的年份之間年雷暴日變化情況明顯的主要有1966、1987、1998年。對54a年雷暴日數據運用(最小二乘法)計算得到一次線性方程為：y=-0.3248x+678.39，其中氣候傾向率為-3.248d/10a，表示鹽城地區從1960年開始，年雷暴日總體上呈現出遞減趨勢，每10a減少3.248d。

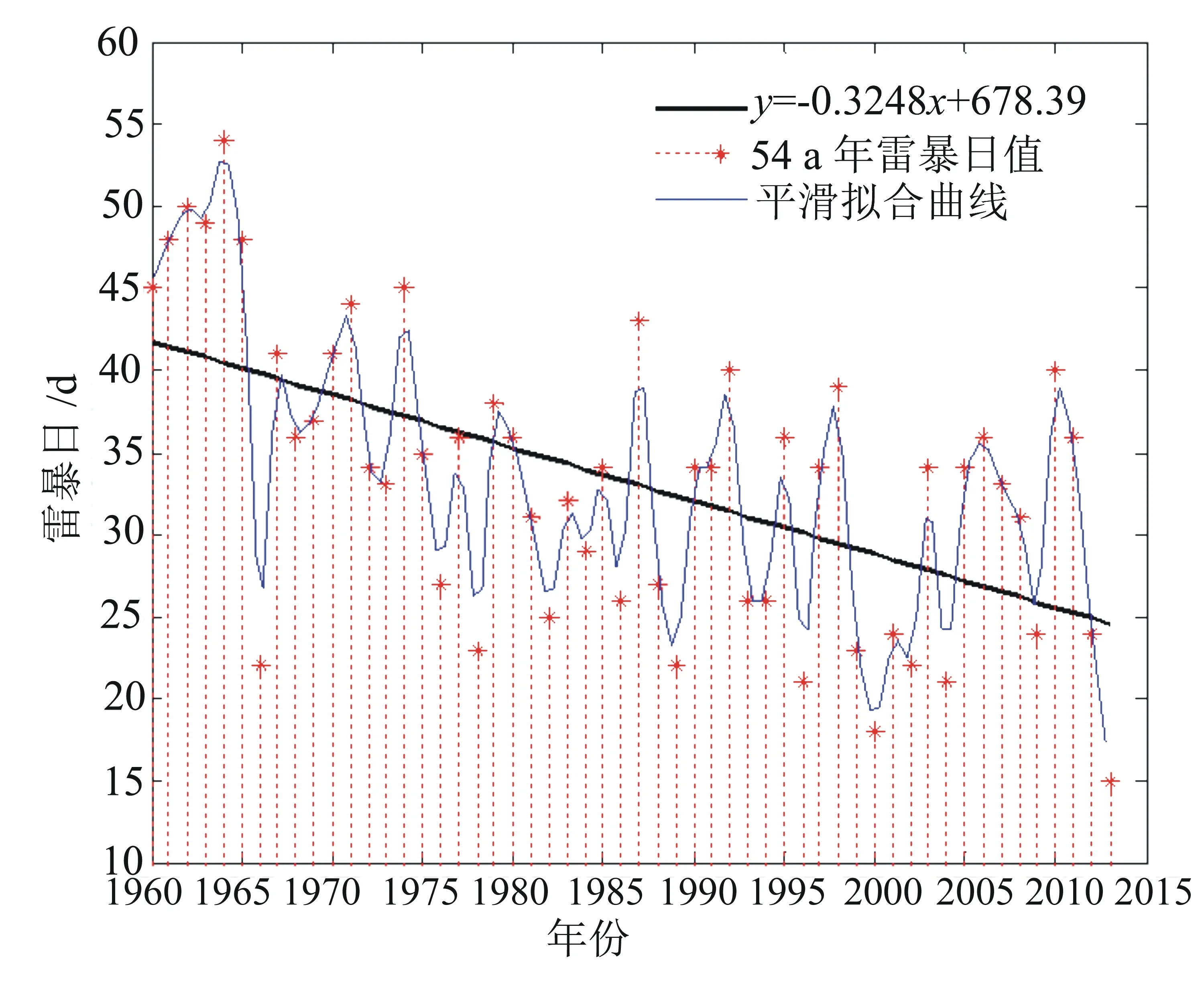
圖1 鹽城地區1960～2013年年雷暴日序列變化圖

在圖2滑動t突變檢驗圖中，發現在1966年發生了一次較為顯著的突變，顯著水平為0.01。可以得出鹽城地區54a年雷暴日在1966年發生一次顯著水平超過99%的突變。

2.2 鹽城地區雷暴日序列EEMD分析結果

對鹽城地區54a年雷暴日數據進行EEMD法分解，所使用的白噪聲的選用為100組標準差為0.01的序列。分析得到1個趨勢項r和4個不同尺度的固有模態函數IMFs，可見原始信息包含了不同尺度的變化特征，如圖3所示。

根據圖3中基于EEMD對鹽城地區54a年雷暴日變化趨勢分解圖可得，IMFn(n=1,2,3,4)波動頻率與幅值逐漸減小。r代表的趨勢分量如圖1顯示的一次函數趨勢近似均為逐漸減少的總趨勢。

HHT變換中邊際譜表示的是信號的某一頻率在各個時刻的幅值之和，這意味著可以比較準確地反映信號的實際頻率成分[13]。因此為探究年雷暴日序列值的周期性變化規律，對年雷暴日序列值的變化求出其邊際譜具有重要實用價值。由于IMF是一種極值點數、過零點數均相等對稱包絡線，為確定每個IMFn(n=1,2,3,4)的周期，對其極大值點數和數據總量進行統計，計算公式如下[7]：

(10)

根據公式(10)，求得的IMFn(n=1,2,3,4)平均周期見表1。

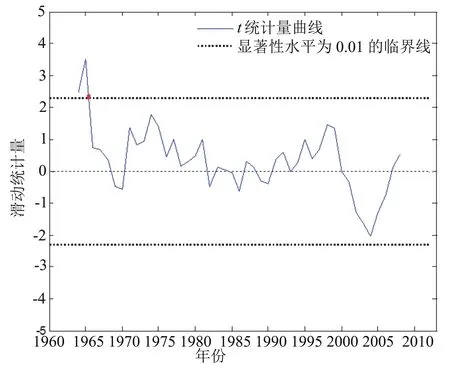
圖2 鹽城地區1960～2013年雷暴日滑動t突變圖

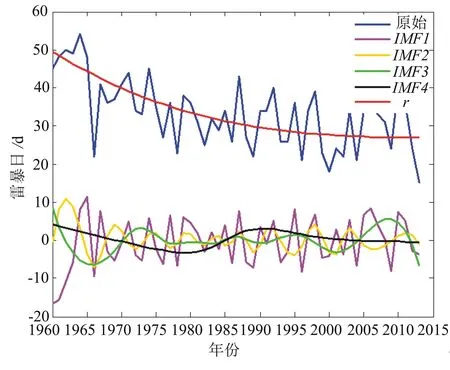
圖3 基于EEMD對鹽城地區54 a年雷暴日變化趨勢分解圖

由表1所列，IMFn(n=1,2,3,4)中心頻率分別是0.45、0.19、0.09、0.04 Hz，相應求得鹽城地區年雷暴日存在2種尺度周期變化，分別是年際變化(5.4 a、2.22 a)和年代際變化(27 a、10.8 a)。

圖4為經過EEMD分解后，進行希爾伯特黃變換法(HHT-Huang)變換后得到的54年雷暴日的Hilbert譜圖(圖4-a)、邊際譜圖(圖4-b)。由圖4-a可得，在頻率范圍為0～0.05 Hz和0.45～0.50 Hz之間出現較為均勻集中的紅色標記點。在0.05～0.45 Hz之間也出現了部分標記點，但是標記點的分布顯得較為分散。圖4-b是邊際譜，其可以顯著展示各個頻率段在整個時間尺度上的能量變化[17]，可見能量較高的幅值部分的分布同樣是在0～0.05 Hz和0.45～0.50 Hz之間。因此，推斷主要的周期范圍存在于2.0～2.2 a的年際尺度和20年以上的代際尺度2個區間。綜上分析，鹽城地區54 a年雷暴日的變化周期主要為：2.22 a的年際周期和27 a的年代際周期。

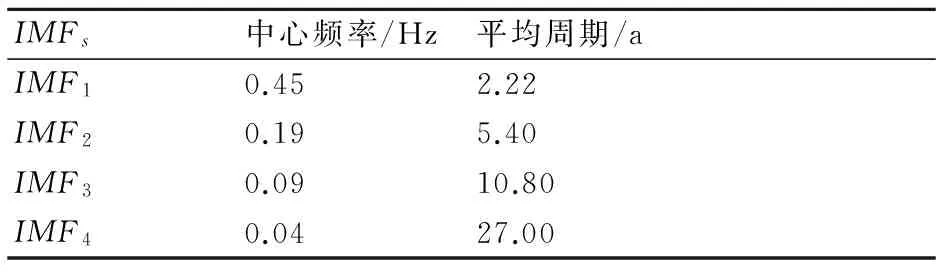
表1 各階IMF分量統計特征值

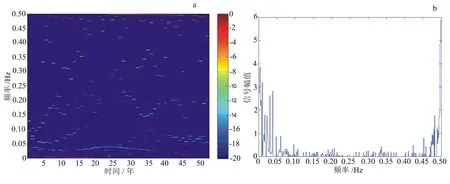
圖4 鹽城地區54 a年雷暴日的Hilbert譜、邊際譜圖

3 研究結果誤差分析

EEMD是EMD算法的拓展和延續，它具有EMD的自適性，同時也由于加入高斯白噪聲解決的尺度混疊的問題。對分解后的IMFn(n=1,2,3,4)數據進行序列疊加重構，來判斷本文分析結果的準確度以及與原始數據的誤差百分比。由圖5-a可知為重構信號與原始信號2條曲線幾乎重疊，難以分辨。將重構波形與原始波形進行對比誤差百分比分析，結果顯示，對比誤差的百分比在整個時間序列上始終保持在±0.8%范圍內，即千分之一的量級。因此，對原始信號的變換失真度幾乎沒有影響。

圖5 基于IMFn重構波形與原始波形的對比與誤差圖

4 研究結果顯著性檢驗分析

圖6為各階IMF趨勢的顯著性檢驗圖，它可以判別通過EEMD分解后得到的IMF分量是具有實際意義的分量還是僅為單純的噪音分量。從圖6可知，C、D點處于B點以下，可信水平低于95%。B點較C、D點幾乎處于95%的置信區間，可信水平為95%。E點則處于95%～99%置信區間之間。因此B點與E點的可信度最高(95%)，即IMF1分量和IMF4分量更具有顯著性統計意義，這與根據IMFs分量中心頻率得到的結果一致。

5 年雷暴日長期預測

根據1960～2013年鹽城地區年雷暴日數據，計算出其轉移矩陣[18]，運用漸近性計算出未來若干年當地雷暴日分布概率，對鹽城地區年雷暴日進行長期預測。

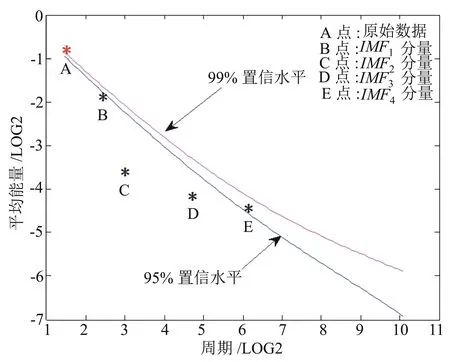
圖6 各階IMF趨勢的顯著性檢驗

首先將雷暴日劃分為以下4個等級：第1級，雷暴日天數≤15 d，其編碼為1；第2級，雷暴日天數15～25 d，編碼為2；第3級，雷暴日天數25～35 d編碼為3；第4級，雷暴日天數≥35 d，編碼為4。通過對鹽城地區1960～2013年的雷暴日數據等級劃分，計算出鹽城地區年雷暴日各等級轉移規律，具體見表2。

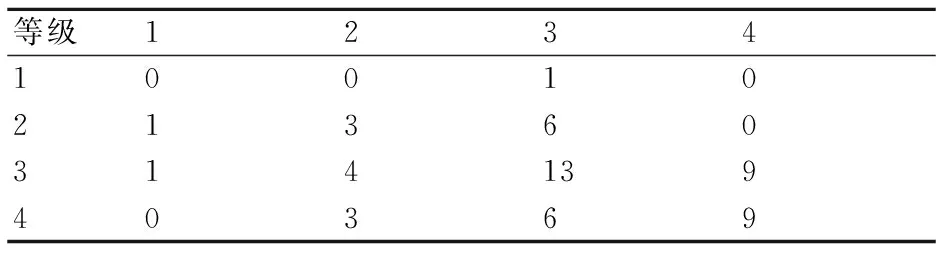
表2 鹽城地區年雷暴日各等級轉移規律

由表2可得一步轉移概率p：

令n=0代表1960年，n=1代表1961年，以此類推，令{X(n),n=0,1,2,3,…}表示鹽城地區年雷暴日1960年以后各年雷暴日，顯然為齊次馬爾科夫鏈，由此計算出各年雷暴日預測等級：

因為轉移概率具有漸近性質，即極限概率分布，所以當n趨向無窮大時，p(n)趨近于固定的一組概率，及其預測的概率分布趨向于一組固定的概率分布。

通過matlab編程求解出當n趨向于無窮時，p(n)概率分布(圖7)。從圖7中可以看出未來鹽城地區雷暴日數主要分別在25～35d之間，其概率達到45%。其次是雷暴日數大于35d的天數段，分布概率達到32%。換而言之，鹽城地區未來的雷暴日基本分布在25d以上。

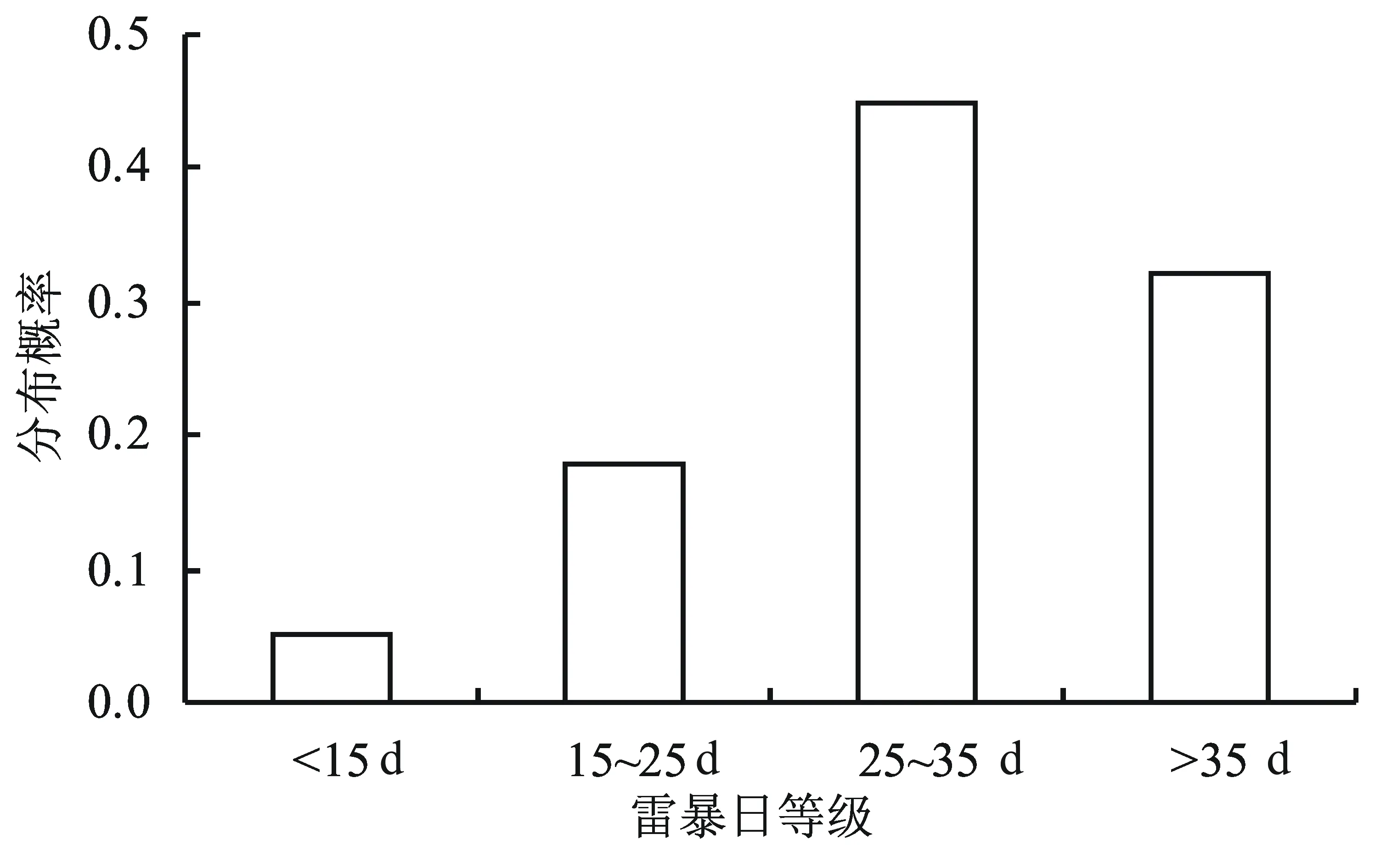
圖7 雷暴日數等級概率分別

6 結論

本文利用多種統計分析法對鹽城地區54a年雷暴日時間序列值變化進行了系統的研究，并概括為以下3個結論：

(1)鹽城地區54a年雷暴日變化波動較大，年雷暴日總體趨勢在波動中減少，氣候傾向率為-3.248d/10a。滑動t突變檢驗發現在1966年發生一次顯著水平超過99%的突變。

(2)基于EEMD的鹽城地區54年雷暴日數據分解成4個IMF分量和1個趨勢分量。結合HHT譜變換，54a年雷暴日的變化主要有2.22a的年際周期和27a的年代際周期，并通過95%顯著性檢驗。重構變化曲線與原始數據對比誤差百分比數量級僅為0.1%，高斯白噪聲帶來的干擾誤差幾乎可以完全忽略。

(3)基于馬爾科夫鏈預測未來鹽城地區年雷暴日數主要在25～35d內，其分布概率達到45%。其次是年雷暴日數大于35d的天數段，分布概率為32%。

由于閃電資料數據時間尺度較短，以及近3年雷暴日的資料數據還有待進一步整理。因此，文中在對年雷暴日的預測驗證分析和與閃電資料數據進行對比分析方面會以此立足，進一步深入研究。

[1] 央美,旦增格列,達瓦澤仁,等.那曲地區雷暴天氣時空變化特征及影響因素[J].應用氣象學報,2014(6):751-760.

[2] 劉正源,姜蘇,曹洪亮.呼和浩特市雷暴氣候特征及其變化分析[J].江西農業學報,2013，25(2):79-82.

[3] 王紀軍,郭紅晨,盧廣建.河南省雷暴日數時空分布的非均一性特征[J].自然災害學報,2009,18(4):115-119.

[4] 左迎芝，孫健，韓通，等.基于兩種觀測資料的雁江區閃電活動規律分析[J].江西農業學報,2016,28(7):116-120.

[5] 王學良,張科杰,張義軍,等.雷電定位系統與人工觀測雷暴日數統計比較[J].應用氣象學報,2014(6):741-750.

[6] 高燚,周方聰,勞小青.1999～2011年海南島雷電災害特征分析[J].自然災害學報,2014，23(5):253-262.

[7] 王兵,胡婭敏,杜堯東,等.小波分析和EEMD方法在廣州氣溫及降水的多尺度分析中的差異分析[J].熱帶氣象學報,2014,30(4):769-776.

[8] 馮民學,周宇,虞敏,等.2013年江蘇省ADTD閃電定位系統資料的評估分析[J].科學技術與工程,2015,15(7):79-84.

[9] 朱寧輝,白曉民,董偉杰.基于EEMD的諧波檢測方法[J].中國電機工程學報,2013,33(7):92-98.

[10] 劉宇峰,原志華,吳林,等.基于濕潤指數的近55年安康地表干濕變化趨勢及周期研究[J].自然災害學報,2016,25(3):11-21.

[11] 時世晨.EEMD時頻分析方法研究和仿真系統設計[D].上海：華東師范大學,2011:11-34.

[12] 陳則煌,張云峰,謝菲,等.EEMD在雷暴日趨勢特征分析中的應用[J].熱帶地理,2015,35(4):601-606.

[13] Huang N E, Shen Z, Long S R. A new view of nonlinear water waves: the hilbert spectrum[J]. Annual Review of Fluid Mechanics, 2003, 31(1): 417-457.

[14] 朱正.Hilbert-Huang變換及其在目標方位估計和水聲通信中的應用研究[D].哈爾濱:哈爾濱工程大學,2013:18-40.

[15] Wu Z, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[16] Putze A, Derome L, Donato F, et al. A markov chain monte carlo technique to sample transport and source parameters of Galactic cosmic rays[J]. Memorie Della Societa Astronomica Italiana, 2015, 462(1): 863.

[17] 譚善文.多分辨希爾伯特-黃(Hilbert-Huang)變換方法的研究[D].重慶:重慶大學,2001:15-25.

[18] Yan Y Q, Zhang D F. Markov chain model of navigation based on frequence[J]. Application Research of Computers, 2007, 24(3): 41-43.

(責任編輯：曾小軍)

Dynamic and Trend Prediction of Thunderstorm Days in Yancheng Area Based on EEMD and Markov Chain

CHEN Chao1,2, LI Peng-fei2,3,4*, XIAO Wen-an2,4, ZHANG Chun-long2,3,4, LV Dong-bo3,4

(1. Meteorological Bureau of Dafeng District, Yancheng City, Jiangsu Province, Yancheng 224100, China; 2. Key Laboratory of Aerosol and Cloud Precipitation, Chinese Meteorological Administration, Nanjing 210044, China; 3. Meteorological Disaster Prevention Technology Center of Heilongjiang Province, Harbin 150030, China; 4. Laboratory of High-latitude Lightning, Chinese Academy of Meteorological Sciences, Harbin 150030, China)

Through adopting the movingt-mutation test, EEMD (Ensemble Empirical Mode Decomposition) and Markov chain statistic model, the author studied the dynamic and trend prediction of annual thunderstorm day number in the past 54 years in Yancheng area, and conducted the significance and error test for the periodicity research results. The results indicated that the annual thunderstorm day number in the past 54 years in Yancheng area revealed a decreasing trend, and the mutation year was 1966. The sequence of annual thunderstorm day number in 54 years could be decomposed into fourIMF(Intrinsic Mode Function) components and a trend component. There existed two main frequency scopes: 0～0.05 Hz and 0.45～0.50 Hz, and their corresponding period was 2.22 years and 27 years (their reliability all exceeded 95%). The error percentage between the reconstructed thunderstorm day data by EEMD and the original thunderstorm day data ranged from -0.8% to 0.8%. The long-period prediction by Markov chain shows that the probability which the number of annual thunderstorm days in the future is 25～35 d will be about 45%, and the probability which the number of annual thunderstorm days in the future is over 35 d will be about 32%.

Yancheng area; Annual thunderstorm day; EEMD; Hilbert transform; Markov chain

2017-02-28

國家自然科學基金資助項目(41175003)；江蘇高校優勢學科建設工程資助項目(PAPD)；黑龍江省氣象局青年英才項目。

陳超(1987─)，男，江蘇鹽城人，碩士研究生,研究方向：氣象數據挖掘統計與雷電防護技術。*通訊作者：李鵬飛。

P44

A

1001-8581(2017)06-0094-06