一種基于八叉樹的快速體素化方法*

段偉偉，羅健欣，倪桂強(qiáng)，唐 斌

(解放軍理工大學(xué) 指揮信息系統(tǒng)學(xué)院，江蘇 南京 210007)

?

一種基于八叉樹的快速體素化方法*

段偉偉，羅健欣，倪桂強(qiáng)，唐 斌

(解放軍理工大學(xué) 指揮信息系統(tǒng)學(xué)院，江蘇 南京 210007)

當(dāng)前的體素化方法大都具有較高的復(fù)雜性，計(jì)算開銷大，對(duì)硬件要求高。為了簡(jiǎn)單快速地實(shí)現(xiàn)3D模型的體素化，提出一種基于八叉樹的快速體素化方法。首先在使用八叉樹進(jìn)行模型細(xì)分的基礎(chǔ)上，得到模型表面數(shù)據(jù)。然后根據(jù)表面數(shù)據(jù)選擇多個(gè)方向?qū)δＰ瓦M(jìn)行逐行掃描。該方法能快速地區(qū)分出模型的外部數(shù)據(jù)和內(nèi)部數(shù)據(jù)，最終實(shí)現(xiàn)模型的體素化。對(duì)不同分辨率下的多種模型的實(shí)驗(yàn)結(jié)果表明，文中提出的方法能有效地實(shí)現(xiàn)快速體素化，具有一定的應(yīng)用價(jià)值。

體素化；八叉樹；快速；多方向逐行掃描；模型細(xì)分

0 引言

近年來，基于體素(Voxel)的3D模型在眾多領(lǐng)域(如立體渲染、虛擬現(xiàn)實(shí)、醫(yī)學(xué)影像、機(jī)械零件制造、流體力學(xué)等)得到了廣泛的應(yīng)用。傳統(tǒng)的3D模型表示方法(如掃描表示法、邊界表示法等)只能表示物體的表面信息，難以描述其內(nèi)部屬性。體素化(Voxelization)能根據(jù)3D模型的表面幾何信息，計(jì)算并獲取模型的內(nèi)部數(shù)據(jù)，產(chǎn)生描述完整3D模型的體數(shù)據(jù)集。目前，作為一個(gè)研究熱點(diǎn)，關(guān)于體素化方法的研究成果越來越多，可以較好地將3D模型表面數(shù)據(jù)轉(zhuǎn)換為能描述模型內(nèi)部信息的體數(shù)據(jù)。然而，這些已有的方法一般具有較高的復(fù)雜性，計(jì)算開銷大，對(duì)硬件要求高。為此，本文提出了一種簡(jiǎn)單的基于八叉樹的快速體素化方法，在利用八叉樹對(duì)3D模型進(jìn)行細(xì)分的基礎(chǔ)上，對(duì)模型的表面數(shù)據(jù)進(jìn)行多方向逐行掃描，快速地區(qū)分出模型的外部數(shù)據(jù)與內(nèi)部數(shù)據(jù)，有效地實(shí)現(xiàn)模型的體素化。

1 相關(guān)工作

1.1 八叉樹

八叉樹是一種空間分割的層次數(shù)據(jù)結(jié)構(gòu)，它將其節(jié)點(diǎn)遞歸地分解為8個(gè)子節(jié)點(diǎn)，直至達(dá)到一定精度[1]。樹的第一個(gè)節(jié)點(diǎn)是根節(jié)點(diǎn)，對(duì)應(yīng)一個(gè)立方體，表示整個(gè)物體模型。每個(gè)節(jié)點(diǎn)有8個(gè)子節(jié)點(diǎn)或者沒有子節(jié)點(diǎn)，這8個(gè)子節(jié)點(diǎn)是對(duì)父節(jié)點(diǎn)的一次2×2×2規(guī)則細(xì)分，其中沒有子節(jié)點(diǎn)的節(jié)點(diǎn)叫做葉節(jié)點(diǎn)。在一個(gè)3D模型的八叉樹結(jié)構(gòu)中，那些包含了模型表面的節(jié)點(diǎn)被更細(xì)致地劃分，而余下的空節(jié)點(diǎn)則成為葉節(jié)點(diǎn)。八叉樹結(jié)構(gòu)的每個(gè)維度上每細(xì)分一次，其分辨率都增大到原來的兩倍。因此，要達(dá)到一個(gè)1283的分辨率，每個(gè)維度上均需要7層細(xì)分操作(log2128=7)。八叉樹結(jié)構(gòu)是表達(dá)三維模型的一種重要方法，能方便有效地進(jìn)行三維模型的表示。

1.2 體素化

體素化也被稱作三維掃描轉(zhuǎn)換(3D Scan Conversion)，最早是由Kaufman在1987年提出[2]，其根據(jù)3D模型的表面數(shù)據(jù)，轉(zhuǎn)換成指定精度的體素表示形式，以獲得包含模型內(nèi)部信息的體數(shù)據(jù)集。

體素化自出現(xiàn)以來，眾多研究者提出了許多不同的體素化方法。Huang等[3]以基于模型表面的法向量函數(shù)為距離標(biāo)準(zhǔn)，將多邊形模型離散為體素模型，可以選擇實(shí)現(xiàn)6-鄰域封閉或26-鄰域封閉。Jones等[4]應(yīng)用距離變換和距離場(chǎng)的方法生成體素模型，主要針對(duì)CT和MRI等產(chǎn)生的灰度體數(shù)據(jù)集體素模型，便于后續(xù)的可視化處理。Dachille等[5]提出一種增量式三角形的體素化方法。Haumont等[6]提出一種基于種子填充方式的實(shí)體體素化方法。Beckhaus等[7]提出了一種切面法，根據(jù)Z軸方向的分辨率設(shè)定一組裁剪面，依次繪制每個(gè)切片并保存在幀緩存中，所有的像素?cái)?shù)據(jù)構(gòu)成了最終的體素化數(shù)據(jù)。Thon等[8]運(yùn)用四叉樹結(jié)構(gòu)對(duì)基于光線投射的體素化算法進(jìn)行了改進(jìn)。吳曉軍等[9-10]利用八叉樹編碼的特性，提出一種產(chǎn)生整個(gè)三維模型的體素表示算法。Laine[11]研究了拓?fù)浣Y(jié)構(gòu)在體素化過程中的應(yīng)用，提出一種基于拓?fù)浣Y(jié)構(gòu)的體素化方法。近些年隨著圖形處理器GPU的快速發(fā)展，一些研究者嘗試將GPU技術(shù)應(yīng)用到體素化方法研究中[12-13]。Martin等[14]提出一種基于GPU的核外(out-of-core)體素化方法，能有效處理高分辨率下的模型。這些方法雖然利用GPU的并行特性提高了算法性能，但是其算法的判斷過程較為復(fù)雜，計(jì)算開銷較大，對(duì)硬件要求較高。

2 基于八叉樹的快速體素化方法

本文針對(duì)一般3D模型的體素化需求，提出了一種基于八叉樹的快速體素化方法。該方法分為兩個(gè)階段：第一階段，使用八叉樹結(jié)構(gòu)對(duì)初始的3D模型進(jìn)行空間細(xì)分，直至達(dá)到指定的分辨率精度，得到在該精度下模型表面對(duì)應(yīng)的體素?cái)?shù)據(jù)；第二階段，提出一種簡(jiǎn)單的多方向逐行掃描算法，能夠根據(jù)3D模型的表面數(shù)據(jù)，快速地區(qū)分模型外部數(shù)據(jù)和內(nèi)部數(shù)據(jù)，進(jìn)而獲得體數(shù)據(jù)集，實(shí)現(xiàn)模型的體素化。

2.1 基于八叉樹的模型細(xì)分

對(duì)于3D模型，首先使用八叉樹對(duì)其進(jìn)行空間細(xì)分，直至得到指定的分辨率。圖1表示對(duì)模型節(jié)點(diǎn)從第l層到第l+1層的細(xì)分過程，相應(yīng)的分辨率從2l提高到2l+1。在最高分辨率層，那些與模型表面相交的節(jié)點(diǎn)將被標(biāo)記為模型表面點(diǎn)，而其余的節(jié)點(diǎn)被標(biāo)記為非表面點(diǎn)。以此可以將所有空間數(shù)據(jù)劃分為兩類：第1類，模型表面點(diǎn)對(duì)應(yīng)的體素?cái)?shù)據(jù)，標(biāo)示為1，即表示3D模型的表面數(shù)據(jù)；第2類，除第1類以外的所有體素?cái)?shù)據(jù)，標(biāo)示為0，包括3D模型內(nèi)部的元素和模型外部的元素。在本階段暫時(shí)不對(duì)模型的內(nèi)部數(shù)據(jù)和外部數(shù)據(jù)進(jìn)行區(qū)分。不同類型的元素劃分如下：

(1)

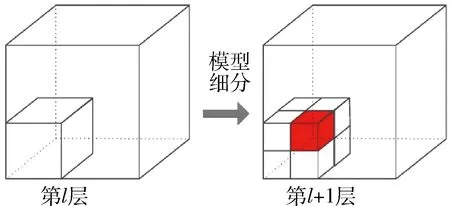
圖1 模型細(xì)分過程

2.2 多方向逐行掃描算法

在上一小節(jié)已經(jīng)獲得了3D模型的表面數(shù)據(jù)。在本節(jié)中，提出了一種簡(jiǎn)單的多方向逐行掃描算法。使用該算法，能根據(jù)3D模型的表面數(shù)據(jù)，快速地區(qū)分出模型的內(nèi)部元素和外部元素，實(shí)現(xiàn)模型體素化。

為簡(jiǎn)單起見，首先給出多方向逐行掃描算法在2D空間中的描述。對(duì)于二維平面中的一個(gè)物體，在已知物體邊界數(shù)據(jù)的情況下，如何區(qū)分其外部數(shù)據(jù)與內(nèi)部數(shù)據(jù)。此處考慮依次選擇不同方向，從空間邊界開始逐行對(duì)物體進(jìn)行掃描。一般地，由于模型空間邊界的元素不在模型內(nèi)部，因此在每一行的掃描過程中，將遇到的非物體邊界元素標(biāo)記為物體的外部元素，直至遇到物體邊界元素時(shí)停止該行掃描。圖2是分別從坐標(biāo)平面的X、Y軸的正、負(fù)方向?qū)ξ矬w進(jìn)行逐行掃描判斷的示意圖。

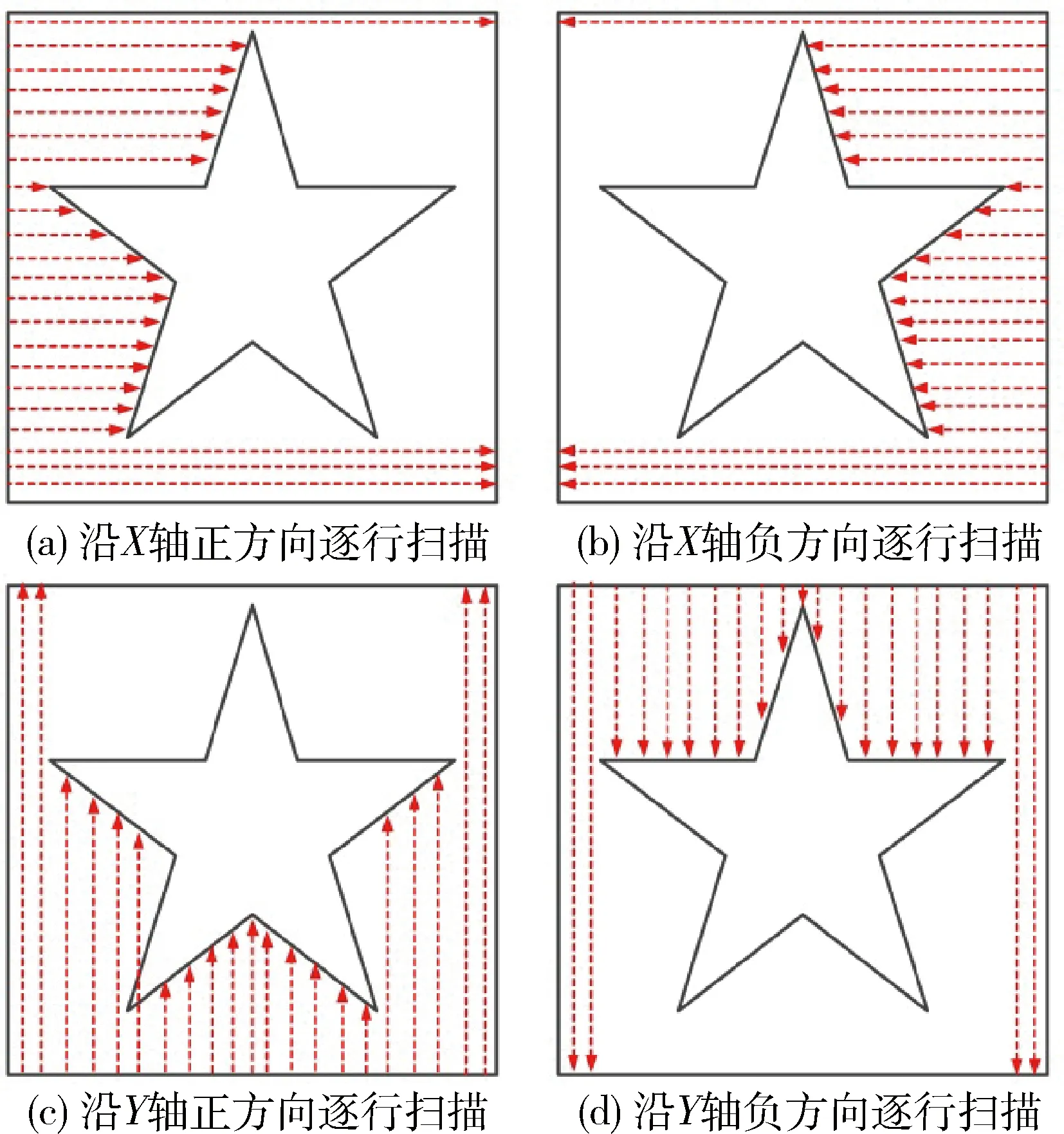
圖2 多方向逐行掃描的二維示意

在經(jīng)過4個(gè)不同方向的逐行掃描遍歷之后，所有的外部元素被區(qū)分出來。對(duì)于整個(gè)數(shù)據(jù)域而言，除去物體的邊界元素和外部元素，其余的元素即為物體的內(nèi)部數(shù)據(jù)。對(duì)內(nèi)部數(shù)據(jù)進(jìn)行賦值填充，即實(shí)現(xiàn)了物體內(nèi)部數(shù)據(jù)的識(shí)別與判定，如圖3所示。

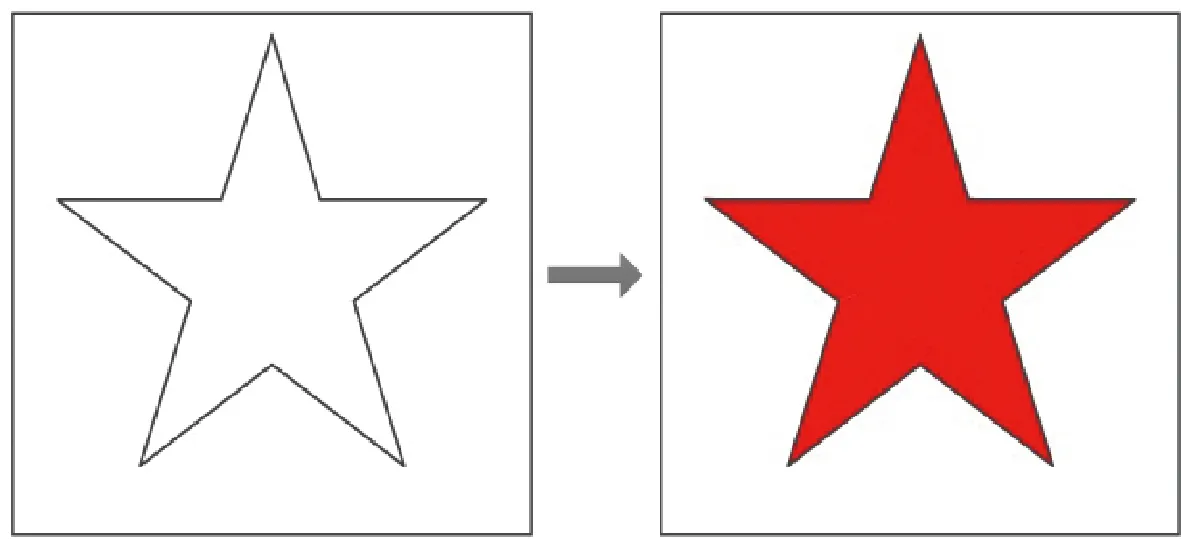
圖3 根據(jù)掃描結(jié)果，填充物體內(nèi)部數(shù)據(jù)

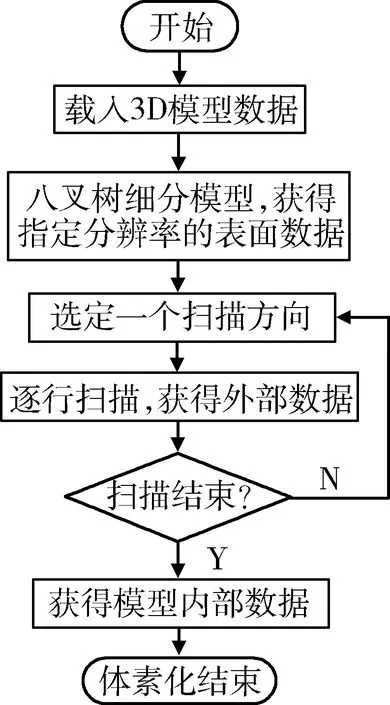
將上述2D空間中的多方向逐行掃描算法推廣到3D空間，將平面坐標(biāo)軸的4個(gè)掃描方向擴(kuò)展到空間坐標(biāo)軸的6個(gè)掃描方向，即可快速實(shí)現(xiàn)對(duì)3D模型內(nèi)部數(shù)據(jù)的識(shí)別與填充，完成3D模型的體素化。分別選擇模型所在的空間坐標(biāo)系的X、Y、Z軸的正、負(fù)方向，從邊界開始對(duì)模型進(jìn)行逐行掃描。首先選擇一個(gè)掃描方向，比如Z軸正方向((0,0,0)→(0,0,z))，在選定的方向上，對(duì)每個(gè)元素進(jìn)行如下判斷：如果該元素值為0，即判定其為模型外部元素，將其值重新標(biāo)示為-1；如果該元素值為1，說明遇到了模型表面，則停止該行的掃描，并開始下一行的掃描；如果元素為-1，說明遇到的是模型外部元素，不做任何處理，繼續(xù)下一個(gè)元素的掃描判定。3D模型的多方向逐行掃描算法的偽代碼如下所示：

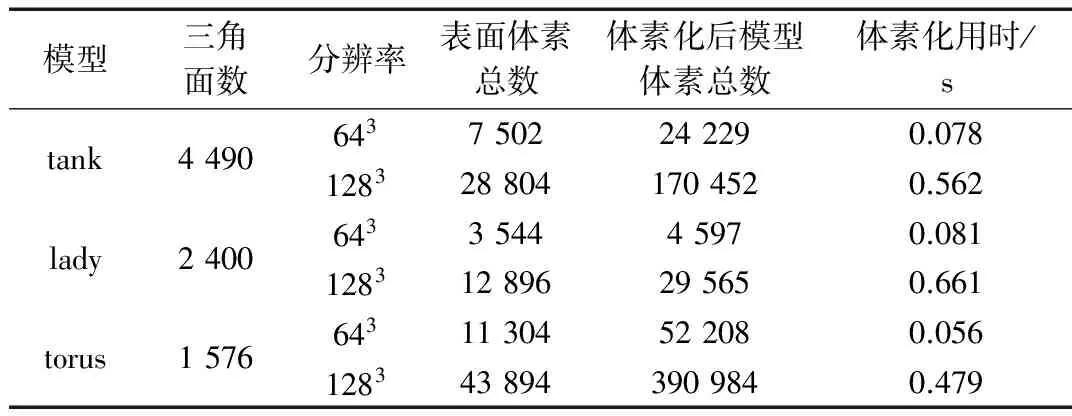
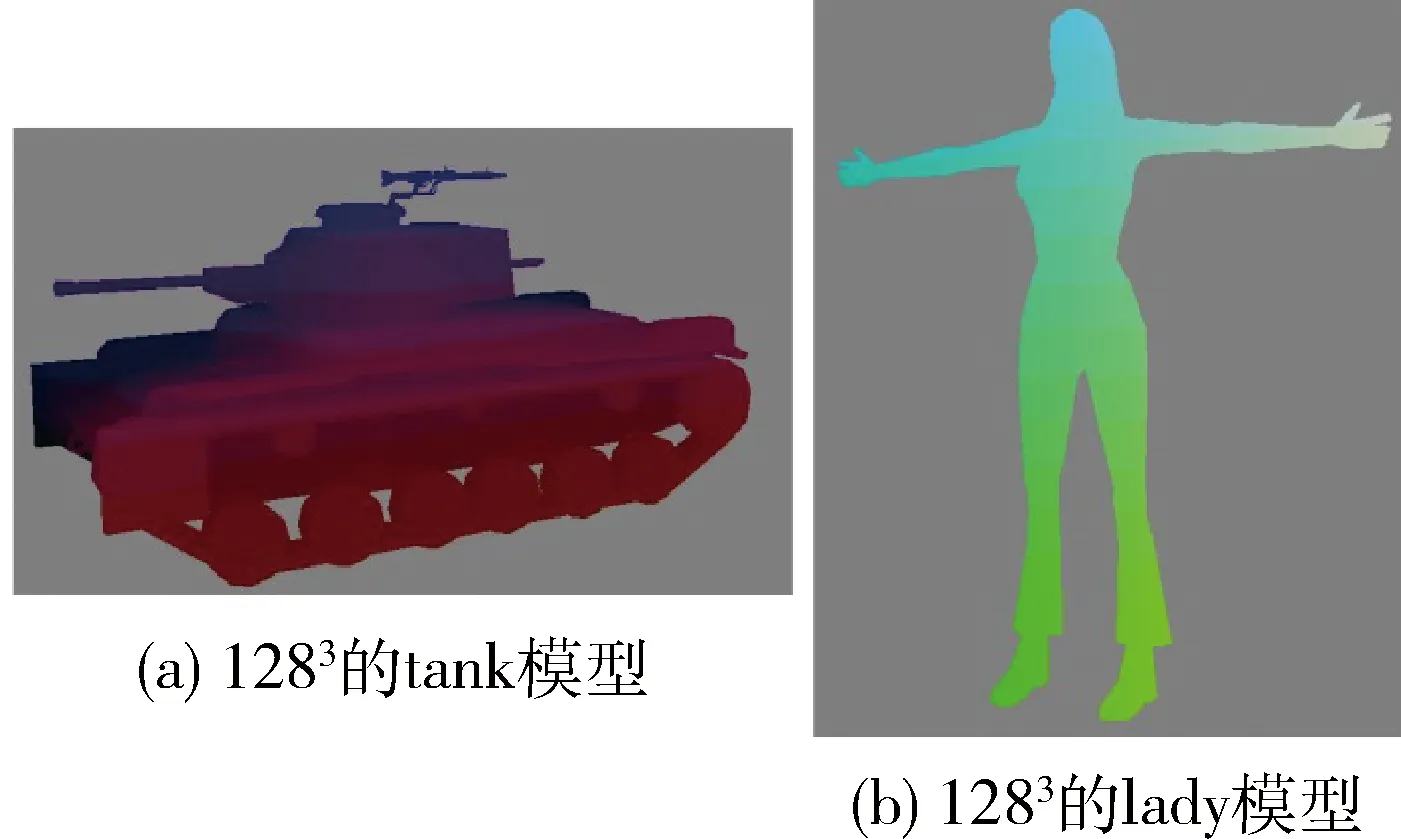
select a scanning direction, such as (0,0,0) to (0,0,z);

for (x=0;x

for (y=0; y

for (z=0; z

//(x,y,z) is outside of the model, set it as a outer voxel

if (voxel(x,y,z)==0)

voxel(x,y,z)=-1;

//(x,y,z) is on the model surface, stop scaning on this row

else (voxel (x,y,z)==1)

break;

}

在6個(gè)方向的掃描遍歷完成以后，所有的體數(shù)據(jù)被分為三類：標(biāo)示值為1的模型表面元素、標(biāo)示值為0的模型內(nèi)部元素，以及標(biāo)示值為-1的模型外部元素。至此，得到了那些標(biāo)示值為1和0的數(shù)據(jù)，即能完整描述3D模型表面及其內(nèi)部的體數(shù)據(jù)。

(2)

圖4 算法流程圖

圖4為整個(gè)方法的流程圖。首先，載入3D模型，使用八叉樹進(jìn)行節(jié)點(diǎn)細(xì)分，得到指定分辨率的模型表面數(shù)據(jù)。然后，依次選擇不同的掃描方向，對(duì)模型進(jìn)行逐行遍歷掃描，如果元素值為0，則將其標(biāo)示為-1；如果值為1，則停止該行掃描，開始下一行掃描；如果值為-1，則不處理，繼續(xù)下一個(gè)元素的掃描。最后，掃描結(jié)束得到模型內(nèi)部數(shù)據(jù)，體素化完成。

3 實(shí)驗(yàn)結(jié)果

為了驗(yàn)證本文算法的有效性，對(duì)不同分辨率的多個(gè)3D模型進(jìn)行了體素化測(cè)試。本文算法在Visual Studio 2010環(huán)境下調(diào)用OpenGL函數(shù)庫(kù)實(shí)現(xiàn)，所有的實(shí)驗(yàn)結(jié)果均是在一臺(tái)2.3 GHz Intel Core2 i7-4712處理器、4 GB內(nèi)存、NVIDIA GeForce 840M顯卡的筆記本電腦上測(cè)試獲得。

表1給出了本文算法所使用的實(shí)驗(yàn)?zāi)Ｐ蛥?shù)及其測(cè)試結(jié)果。圖5是分辨率為1283的tank模型和lady模型的體素化效果圖。

表1 模型參數(shù)及體素化測(cè)試結(jié)果

實(shí)驗(yàn)結(jié)果顯示，本文算法在多個(gè)模型的不同分辨率需求下，均能在較快的時(shí)間內(nèi)產(chǎn)生較好的體素化效果。

圖5 3D模型體素化效果圖

4 結(jié)論

本文提出了一種基于八叉樹細(xì)分模型的多方向逐行掃描的體素化方法，首先在使用八叉樹對(duì)3D模型進(jìn)行細(xì)分的基礎(chǔ)上，得到模型表面數(shù)據(jù)，然后根據(jù)表面數(shù)據(jù)進(jìn)行多個(gè)方向的逐行掃描，快速地區(qū)分出模型的外部數(shù)據(jù)和內(nèi)部數(shù)據(jù)，實(shí)現(xiàn)模型體素化。本文算法思路簡(jiǎn)單，易于實(shí)現(xiàn)，對(duì)硬件需求不高。在處理一般的3D模型體素化任務(wù)時(shí)，該算法具有較大的優(yōu)勢(shì)。實(shí)驗(yàn)結(jié)果表明，本文方法可以以較快的速度對(duì)不同分辨率下的多種模型實(shí)現(xiàn)體素化。但是，本文算法并不能很好地處理內(nèi)部包含有空洞的3D模型，會(huì)將內(nèi)部的封閉空洞誤識(shí)別為模型的內(nèi)部體數(shù)據(jù)。

下一步的工作將針對(duì)無法識(shí)別3D模型內(nèi)部封閉空洞的問題，對(duì)多方向逐行掃描算法進(jìn)行改進(jìn)，期望可以正確地識(shí)別出模型的內(nèi)部空洞，進(jìn)一步提高算法的適用性，擴(kuò)大應(yīng)用范圍。

[1] MEAGHER D. Geometric modeling using octree encoding[J]. Computer Graphics and Image Processing, 1982, 19(2):129-147.

[2] KAUFMAN A. Efficient algorithms for 3D scan-conversion of parametric curves, surfaces, and volumes[J]. ACM Siggraph Computer Graphics, 1987, 21(4):171-179.

[3] HUANG J, YAGEL R, KURZION Y. An accurate method to voxelize polygonal meshes[C]. IEEE Symposium on Volume Visualization, 1998:119-126.

[4] JONES M W,SATHERLEY R. Voxelisation: modeling for volume graphics[C]. Conference on Vision Modeling and Visualization, 2000:319-326.

[5] DACHILLE F, KAUFMAN A. Incremental triangle voxelization[C].Proceeding of Graphics Interface, 2000:205-212.

[6] HAUMONT D, WARZEE N. Complete polygonal scene voxelization[J]. Journal of Graphics Tools, 2002, 7(3):27-41.

[7] BECKHAUS S, WIND J, Strothotte H. Hardware-based voxelization for 3D spatial analysis[C].Proceeding of the 5th International Conference on Computer Graphics and Imaging, 2002:15-20.

[8] THON S,GESQUIERE G, RAFFIN R. A low cost anti-aliased space filled voxelization of polygonal object[C].Proceeding of International Conference Graphics, 2004: 71-78.

[9] 吳曉軍，劉偉軍，王天然,等. 改進(jìn)的基于歐式距離測(cè)度網(wǎng)格模型體素化算法[J]. 計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào), 2004, 16(4): 592-597.

[10] 吳曉軍，劉偉軍，王天然,等. 基于八叉樹的三維網(wǎng)格模型體素化方法[J]. 工程圖學(xué)學(xué)報(bào), 2005, 26(4):1-7.

[11] LAINE S. A topological approach to voxelization[J]. Computer Graphics Forum, 2013, 32(4):77-86.

[12] SCHWARZ M, SEIDEL H P. Fast parallel surface and solid voxelization on GPUs[J].ACM Transation on Graphics, 2010, 29(6): 179.

[13] CRASSIN C, GREEN S. Octree-based sparse voxelization using the GPU hardware rasterizer[M]. OpenGL Insights, 2012.

[14] MARTIN P, ANDREAS K. Grid-free out-of-core voxelization to sparse voxel octrees on GPU[C]. Conference on High-Performance Graphics, ACM, 2015:95-103.

A fast voxelization method based on octree

Duan Weiwei, Luo Jianxin, Ni Guiqiang, Tang Bin

(School of Command Information System, PLA University of Science and Technology, Nanjing 210007, China)

Current methods of voxelization almost have extraordinary complexity which need a high cost of calculation and hardware requirements. In order to achieve a simple and fast voxelization of 3D models, this paper presents a fast voxelization method based on octree. Firstly, subdividing the 3D models using octree structure to get the voxel data on the model surface. After selecting multi-directions to scan the model per row according to the surface data, it’s easy to judge that the voxels are inside of the model or outside of the model. Then the voxelization of 3D model is done. The experimental results of several models on different resolutions show that this method achieves a fast voxelization efficiently and is valuable in application.

voxelization; octree; fast; scanning per row of multi-directions; model subdividing

江蘇省自然科學(xué)青年基金(BK20150722)

TP391.4

A

10.19358/j.issn.1674- 7720.2017.11.027

段偉偉，羅健欣，倪桂強(qiáng)，等.一種基于八叉樹的快速體素化方法[J].微型機(jī)與應(yīng)用，2017,36(11)：91-93，101.

2016-12-13)

段偉偉(1988-)，男，博士研究生，主要研究方向：計(jì)算機(jī)圖形學(xué)，算法設(shè)計(jì)。

羅健欣(1984-)，男，博士，講師，主要研究方向：計(jì)算機(jī)圖形學(xué)，可視化，計(jì)算機(jī)網(wǎng)絡(luò)。

倪桂強(qiáng)(1966-)，通信作者，男，博士，教授，主要研究方向：計(jì)算機(jī)網(wǎng)絡(luò)，可視化，計(jì)算機(jī)圖形學(xué)。E-mail:nigq1966@163.com。