2016年高考物理中約束與臨界值問題例析
張延賜 錢呈祥
(1.浙江省溫州中學,浙江 溫州 325000;2.浙江省永嘉縣上塘中學,浙江 永嘉 325100)
2016年高考物理中約束與臨界值問題例析
張延賜1錢呈祥2
(1.浙江省溫州中學,浙江 溫州 325000;2.浙江省永嘉縣上塘中學,浙江 永嘉 325100)
在物理習題中,經常出現某些物理變化在一定的約束條件限制下進行,本文對2016年高考物理中約束與臨界值問題進行剖析.
高考物理;約束問題;臨界值問題
在物理習題中,經常出現某些物理變化在一定的約束條件限制下進行.如果質點受到某種約束,例如被限制在某曲線或曲面上運動,不能脫離該線或面而作任意的運動,則該質點叫非自由質點,該情境中的線或面叫約束,其方程則叫做約束方程,對研究對象的運動軌跡構成限制的物體叫約束物,習題中常見的約束物有軌道、桿、擋板、銷釘或輕繩等,當約束物變化時往往意味著物理過程的改變.限制物理變化的約束條件常可分為明約束和隱約束條件.原題中已經給出約束條件的,叫明約束;原題中沒有直接給出約束條件,需分析推理后,才能找到的約束條件,叫隱約束.此時的問題解決應立足于數學方法,利用約束條件分析物理過程,建立起與未知量相關的方程組,然后求解.現行高中物理教材都未曾明確提及約束問題,然而,有關約束問題的習題卻不少,在2016高考中也出現這類題型,現舉例說明之.
1 有關約束問題
約束既可以是實在的物體,也可以是某些物體對別的物體運動限制作用的抽象.
約束的分類隨依據不同而異.按其約束的方向來分,可分為單向約束和多向約束,如在在圖1甲中,小球在不同時刻都只在沿繩伸長的方向受限制,稱為單向約束;在圖1丙中,帶電小圓環沿絕緣桿在電磁場中下滑時,除沿桿的方向以外,其他方向都受到限制,稱為多向約束.按約束隨時間改變與否,可分為穩定約束與不穩定約束,如在圖1乙中,如果斜面體是固定的,則稱為穩定約束,如果斜面體是放在光滑的水平面上,當m下滑時,斜面體本身也作加速運動,則稱為不穩定約束.力學中把約束物對物體的作用力,稱為約束反力.例如圖1甲中繩子對小球的拉力、圖1乙中斜面對物體的支持力等等都叫做約束反力.
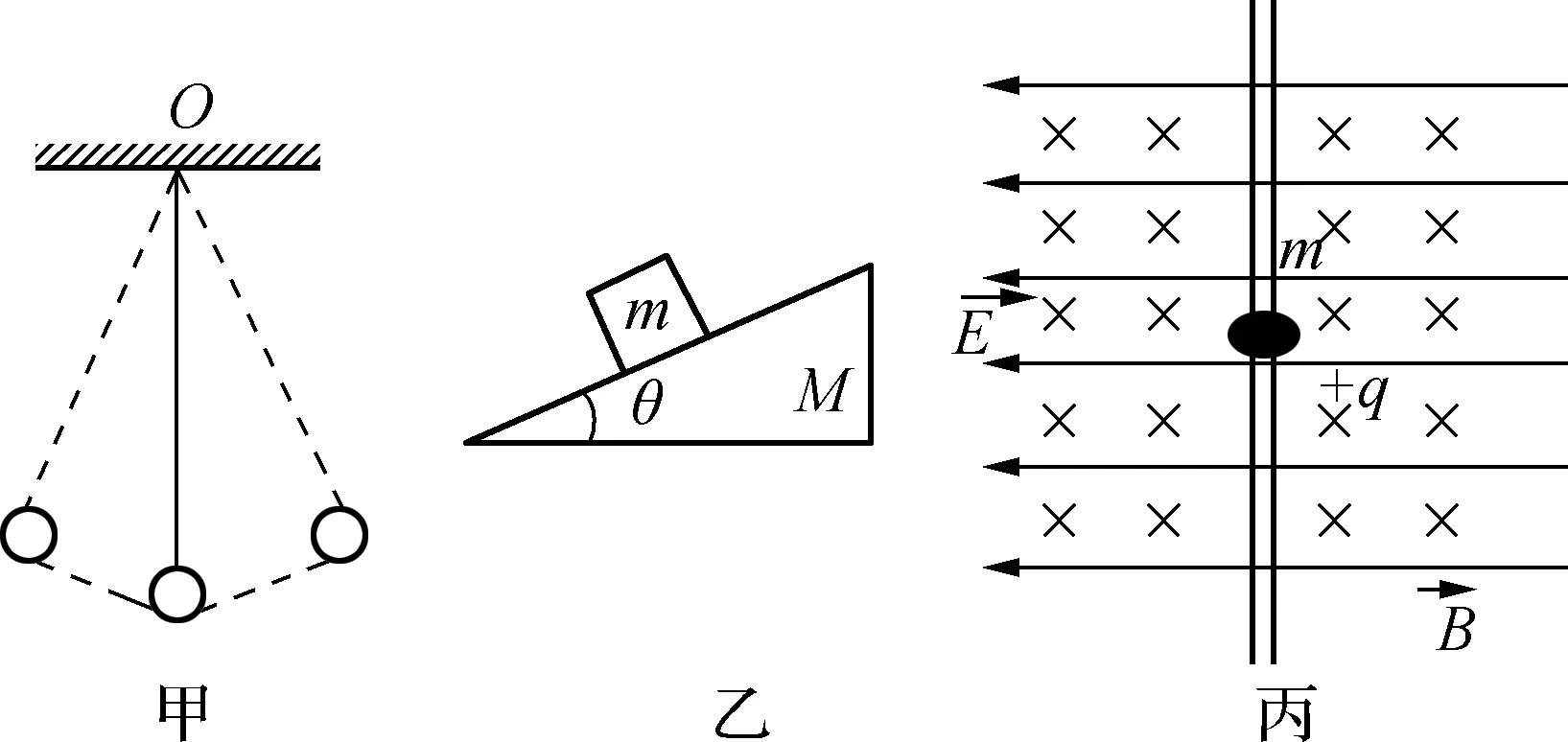
圖1
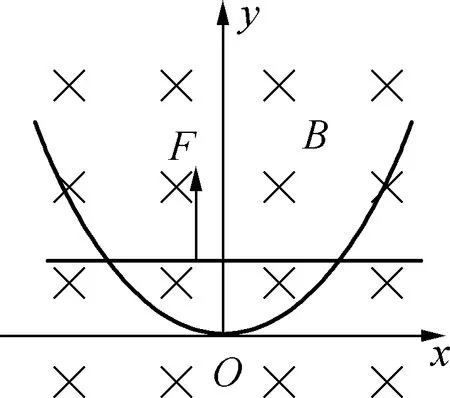
圖2
例1(2016年高考上海卷):如圖2所示,一關于y軸對稱的導體軌道位于水平面內,磁感應強度為B的勻強磁場與水平面垂直.一足夠長,質量為m的直導體棒沿x軸方向置于軌道上,在外力F作用下從原點由靜止開始沿y軸正方向做加速度為a的勻加速直線運動,運動時棒與x軸始終平行.棒單位長度的電阻為ρ,與電阻不計的軌道接觸良好,運動中產生的熱功率隨棒位置的變化規律為P=ky3/2,求:
(1) 導體軌道的軌道方程y=f(x);
(2) 棒在運動過程中受到的安培力Fm隨y的變化關系;
(3) 棒從y=0運動到y=L過程中外力F的功.
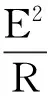
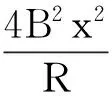
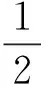
本題根據安培力的功率、勻變速直線運動位移與速度關系,導出軌道的軌道方程和安培力隨y的變化關系,通過動能定理計算棒運動過程中外力做的功.
2 單向約束解除的可能性,即臨界值問題
所謂“臨界狀態”就是指物理現象發生質的飛躍的轉折狀態.與這種狀態相關的一些物理量的值,通常叫臨界值.物理臨界問題雖然在考綱中沒有明確提出,但近幾年來高考的物理試題中較頻繁出現.對于物理臨界問題的考查主要集中在力和運動.臨界問題包含下列幾種情形:① 連接相鄰的物理過程的狀態;② 某些物理量出現極值的狀態;③ 某些物理量的值變為零的狀態.如果約束對物體的限制是單側的,即它只限制物體不得從某一側脫離約束,但卻允許物體從另一側脫離,在這類約束中,約束反力也是單側的.對于這種單側約束,應當注意約束解除的可能性.約束解除問題也稱臨界值問題.在具體問題中,何時解除約束,往往不能預先知道.為了找出約束解除的時刻(或位置)即臨界狀態,常用的方法是:先假定物體不脫離約束、將假設的約束反力代入牛頓運動方程中求解,解出約束反力的表達式后,令其約束反力等于零(這就意味著約束解除),由此可求出相應的時刻或位置.
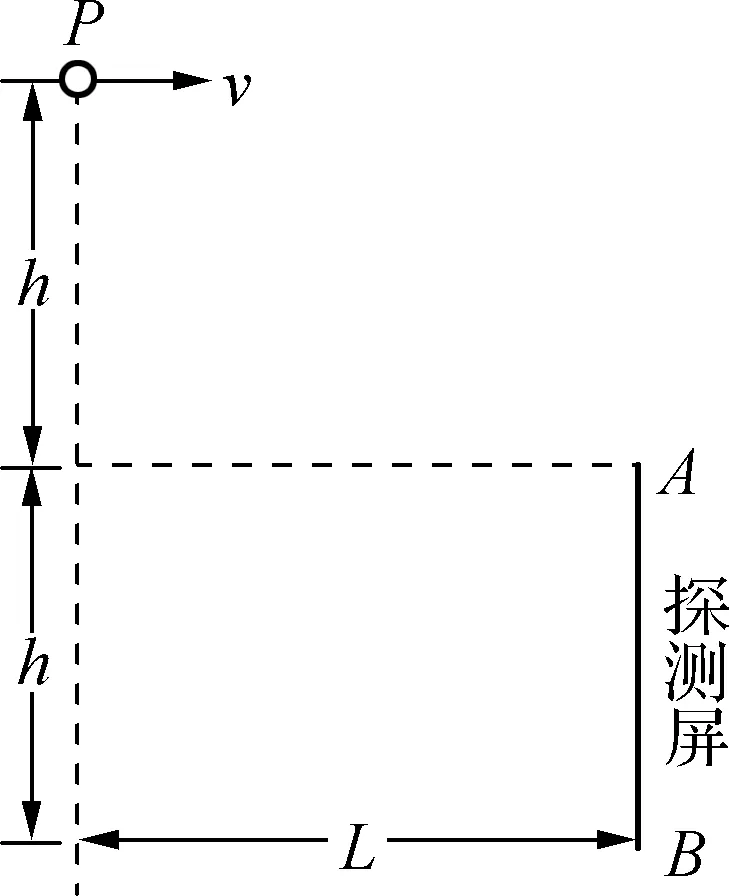
圖3
例2(2016年高考浙江卷):在真空環境內探測微粒在重力場中能量的簡化裝置如圖3所示.P是一個微粒源,能持續水平向右發射質量相同、初速度不同的微粒.高度為h的探測屏AB豎直放置,離P點的水平距離為L,上端A與P點的高度差也為h.
(1) 若微粒打在探測屏AB的中點,求微粒在空中飛行的時間;
(2) 求能被屏探測到的微粒的初速度范圍;
(3) 若打在探測屏A、B兩點的微粒的動能相等,求L與h的關系.
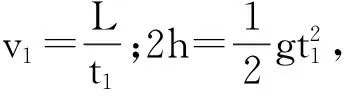
此題是對平拋運動的考查,主要是掌握平拋運動的處理方法,在水平方向是勻速運動,在豎直方向是自由落體運動.解題時注意找到臨界態,此題難度不大,意在考查學生對物理基本方法的掌握情況.
例3(2016年高考天津卷):我國將于2022年舉辦冬奧會,跳臺滑雪是其中最具觀賞性的項目之一,如圖4所示,質量m=60kg的運動員從長直助滑道AB的A處由靜止開始以加速度a=3.6m/s2勻加速滑下,到達助滑道末端B時速度vB=24m/s,A與B的豎直高度差H=48m,為了改變運動員的運動方向,在助滑道與起跳臺之間用一段彎曲滑道銜接,其中最低點C處附近是一段以O為圓心的圓弧.助滑道末端B與滑道最低點C的高度差h=5m,運動員在B、C間運動時阻力做功W=-1530J,取g=10m/s2.
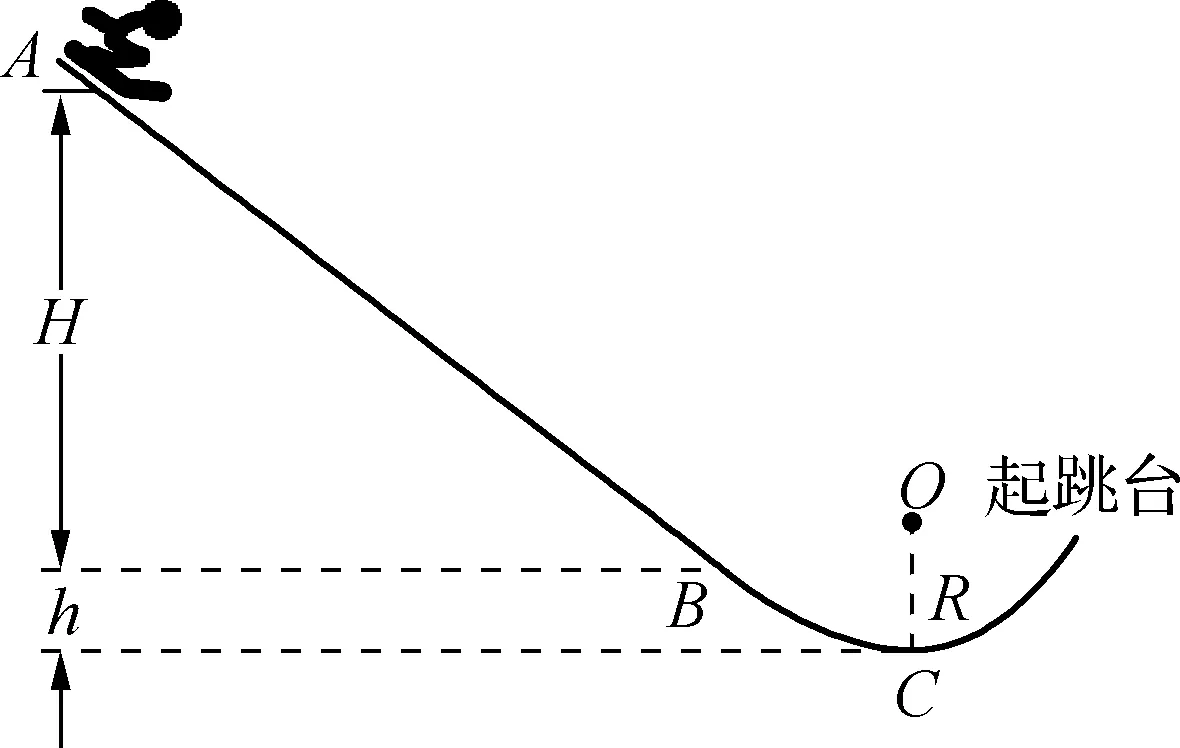
圖4
(1) 求運動員在AB段下滑時受到阻力Ff的大小;
(2) 若運動員能夠承受的最大壓力為其所受重力的6倍,則C點所在圓弧的半徑R至少應為多大.

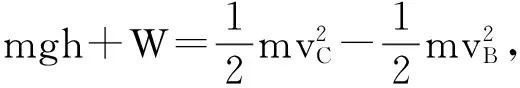
此題是力學綜合題,主要考查動能定理及牛頓第二定律的應用.解題的關鍵是搞清運動員運動的物理過程,分析其受力情況,然后選擇合適的物理規律列出方程求解.注意第(1)問中斜面的長度和傾角未知,這兩個條件相關限制鎖定,設定其中一個物理量即可.求解C點所在圓弧的半徑R至少應為多大,說明本題是臨界值問題,主要考查平拋運動和動能定理的應用以及函數極值的計算,意在考查考生的綜合分析及數學計算能力.
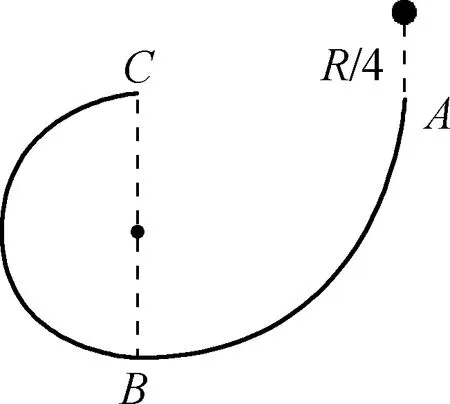
圖5
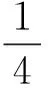
(1) 求小球在B、A兩點的動能之比;
(2) 通過計算判斷小球能否沿軌道運動到C點.
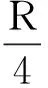
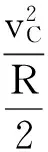
本題需分析清楚小球的運動過程,把握圓周運動最高點臨界速度的條件:重力等于向心力,同時要熟練運用機械能守恒定律.
如表1所示,物理中不同的臨界情況對應著不同的臨界條件.
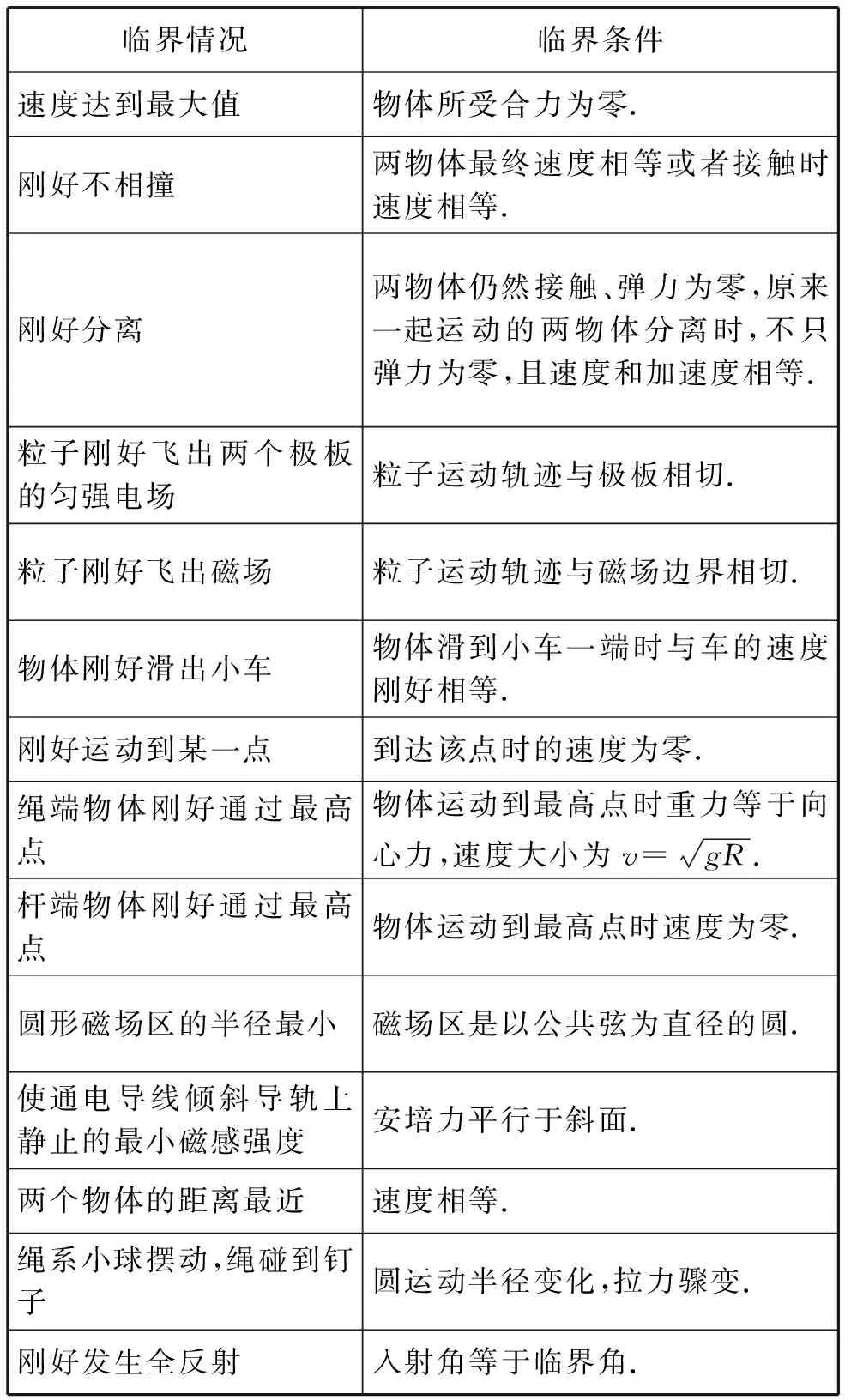
表1
解決臨界問題的基本思路為:
(1) 分析臨界狀態:一般采用極端分析法,即把問題中的物理量推向極值,就會暴露出物理過程.所謂臨界狀態一般是即將要發生質變時的狀態,也是未發生質變時的狀態.
(2) 找出臨界條件:① 相對滑動與相對靜止的臨界條件是靜摩擦力達最大值;② 繩子松弛的臨界條件是繩中拉力為零;③ 相互接觸的兩個物體將要脫離的臨界條件是相互作用的彈力為零.
(3) 列出狀態方程:將臨界條件代到狀態方程中,得出臨界條件下的狀態方程.
(4) 聯立方程求解:有些臨界問題單靠臨界條件下的狀態方程不能解決問題,則需結合其他規律聯立方程求解.
[1] 呂文彬.約束問題與臨界值.中學生理科應試[J],2009,(4).
[2] 趙前山.例談物理習題中約束問題分析解答.中學理科[J],2013,(6).

