基于貝葉斯網絡的網絡風險評估研究

李軍+熊飛+鈕焱

摘要：建立一個基于貝葉斯網絡的風險評估模型，通過風險因素識別、建模和定量計算對網絡運行過程中產生的風險進行評估。選取流量、CPU和內存這3個網絡性能指標參數作為網絡發生風險的定性分析因素，通過貝葉斯網絡來計算出各風險因素造成網絡發生風險的概率并對其進行排序，確定各風險因素對網絡風險的影響程度，并計算出網絡風險率。

關鍵詞：貝葉斯網絡；網絡風險評估；性能指標

中圖分類號：TP309

文獻標識碼：A

文章編號：16727800（2017）004019704

0引言

隨著互聯網的迅猛發展，網絡規模及其應用的復雜性日益加大，網絡及電腦設備的負荷不斷增長，導致網絡性能不斷降低，運行緩慢、系統崩潰等現象時有發生，給用戶帶來了許多風險。網絡風險評估是指對網絡中已知或潛在的安全風險進行探測、識別、計算、評價的過程。通過對網絡風險進行評估，可以了解潛在的危害，有針對性地加以安全防范，從而保障網絡的安全運行。 近年來，風險評估相關研究受到國內外學者的廣泛關注，提出了許多研究方法。孫鵬程、陳吉寧[1]通過貝葉斯網絡直觀地表示事故風險源和河流水質之間的相關性，并用時序蒙特卡洛算法將風險源狀態模擬、水質模擬和貝葉斯網絡推理過程結合，對多個風險源進行量化評估。吳欣[2]提出了一種新的基于貝葉斯網絡的方法有效地處理故障診斷中存在的問題，同時根據提出方法的特點設計了基于多代理系統（MAS）的故障診斷體系結構。閆峰[3]提出基于攻擊圖的網絡安全風險評估方法，將攻擊圖技術應用到網絡安全風險評估中，通過攻擊圖展示攻擊者利用網絡中脆弱性及脆弱性間依賴關系綜合入侵目標網絡的攻擊場景，并在此基礎上計算網絡的安全風險并尋找最小代價的網絡加固措施。由于貝葉斯網絡本質上是一個有序無環圖，基于貝葉斯網絡的概率計算方法也只能適用于無環的攻擊圖，且計算繁雜度為指數級，不適合大規模網絡使用。 國外學者S Kondakci[4]提出了一種基于貝葉斯信念網絡的因果關系評價模型，用來分析和量化由各種威脅源造成的信息安全風險。TT Chen和SS Leu[5]建立了一種基于故障樹轉換的貝葉斯網絡，對橋梁建設項目進行下跌風險評估。S Barua，X Gao[6]等提出了一種基于貝葉斯網絡的動態系統風險評估方法，建立了一個化工過程系統動態故障樹，將它映射到貝葉斯網絡，通過動態貝葉斯網絡來演示動態操作風險評估方法。傳統推理方法不適合確定風險因素的后驗概率，不同專家提供的數據會直接影響精確度和評估質量。 貝葉斯網絡分析方法是一種新的定量分析方法，通過使用概率理論來描述不同因素之間的關系，這種概率推理方法本質上是基于一個有向無環圖，它代表著節點間的概率相關性。并且，它能夠有效地處理現實生活中的不確定性問題。許多專家都使用貝葉斯網絡分析方法來進行風險評估，并應用于交通事故、水污染事故、電力故障和信息安全等。貝葉斯網絡能夠有效地處理不確定性問題，它提供了強大的計算能力，能夠通過已知信息計算未知信息，進而進行有效推理。由于在網絡風險評估方面也有許多不確定性因素，且存在著一定的相似性，故本文使用貝葉斯網絡方法對網絡運行過程中的風險進行評估。

1貝葉斯網絡

1.1貝葉斯網絡的描述

作為描述不確定性信息和推理的最有效理論模型之一，貝葉斯網絡應用于人工智能的幾大分領域包括因果推理、不確定性知識表示、模式識別和分類等，它結合了人工智能、概率理論以及圖形理論，是一種將因果知識和概率知識相結合的信息表示框架。它可以直觀地表達出各風險因素之間的相互關系，便于從不完整或不確定的信息中進行推理。貝葉斯網絡包含2個部分：一個是網絡拓撲結構，另一個是條件概率表。網絡拓撲結構是模型的定性描述部分，是一個有向無環圖，其中每個節點代表論域中的隨機變量，變量之間存在一條有向弧連接相鄰節點，有向弧代表變量間的依賴關系，如果兩個節點之間沒有邊連接，那么它們沒有直接依賴關系相互獨立；節點與其父節點之間的條件概率表用來描述變量之間的關系強度。節點與父節點之間存在一種因果聯系，這種因果聯系可以準確地反映出它們之間的依賴關系。在貝葉斯網絡中，定性信息主要通過網絡的拓撲結構表達，而定量信息主要通過節點的聯合概率密度表示。 貝葉斯網絡的條件獨立性假設是一個非常重要的特性，它顯著地減少了使用先驗概率進行網絡推測的計算難度。對于任何一個節點，當給定它所有父節點的狀態時，該節點與其所有祖先節點條件獨立[7]。

貝葉斯網絡模型構建包括2個步驟：①構建網絡拓撲結構，定性描述各節點之間的因果關系；②構建一個條件概率表，定量描述網絡中各節點的關系強度。

1.2基于貝葉斯網絡模型的網絡風險評估結構

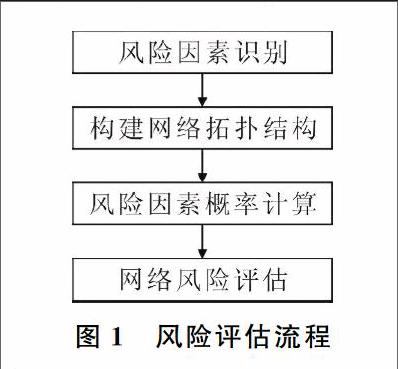
基于貝葉斯網絡的風險評估流程如圖1所示。①風險因素識別，從所有網絡性能指標中，選取適當的幾個指標進行實驗；②構建網絡拓撲結構，通過貝葉斯網絡進行分析，確定各指標之間的依賴關系，畫出貝葉斯網絡拓撲結構圖；③風險因素概率計算，首先，采集數據并進行歸一化處理，得到對應指標某一時間段的時間序列圖，然后進行統計分析，計算出各指標的先驗概率，最后，通過BNT工具箱計算出各指標的后驗概率；④網絡風險評估。通過上述計算結果，結合給定的評估系數公式，求出各指標的φ（xi）并進行排序，最后，計算網絡風險率p（R），結合風險等級表查看當前時刻的網絡風險等級。

1.2.1風險識別在網絡運行過程中，由于用戶使用不當或者網絡攻擊可能造成網絡性能降低，產生網絡風險，網絡風險可能由多種風險因素的相互作用而引起。本文通過相關文獻查閱、實驗調查和數據采集，選取了流量、CPU和內存3個風險因素，對應的狀態如表1所示。

1.2.2網絡拓撲結構構建通過一個鄰接矩陣LJ=（aij）n×n構建網絡結構，當節點i是節點j的父節點時，aij=1；否則aij=0。然后，通過矩陣對角元素來確定最終矩陣。如果，鄰接矩陣的對角元素不全為0，那么該網絡結構就不符合有向無環圖，反之，則適合。由于在網絡運行過程中，流量、CPU、內存的超標都可能引起網絡風險，所以網絡風險與流量、CPU、內存之間存在直接依賴關系。而流量的超標也有可能導致CPU、內存超標，所以CPU、內存與流量之間也存在直接依賴關系。因此，可得到如下鄰接矩陣：

由式（4）可知，鄰接矩陣LJ中所有對角元素均為0，所以該結構是一個有向無環圖，滿足模型需求。因此，圖2中的網絡拓撲結構是一個合理的貝葉斯網絡結構。

其中，節點1代表流量，節點2代表CPU，節點3代表內存，節點4代表網絡風險。

1.2.3風險因素概率計算通過實驗，分別監測一段時間內看視頻、看網頁、下載以及網絡攻擊情況下的網絡性能指標情況，得到流量、CPU、內存的時間序列圖，經過歸一化后如圖3-圖5所示。

現假定流量、CPU、內存超標的臨界值分別為0.7、0.6、0.6[810]，從2 000個數據中分別進行統計，得到各指標的條件概率表（見表2-表5）。

由表2、表3、表4、表5可獲得先驗概率分布，如圖6所示。接下來通過BNT工具箱，輸入流量、CPU、內存的條件概率，得到各指標的后驗概率，如圖7所示。圖6是根據實驗數據統計得出的流量、CPU、內存各狀態發生風險的先驗概率，而圖7是通過BNT工具箱計算得到的當風險發生情況下流量、CPU、內存各狀態發生風險的后驗概率。通過比較圖6和圖7可知，當確定有網絡風險發生時，流量、CPU、內存為True狀態時的概率都增加了，其中流量變化最明顯。通過BNT工具箱還可以得出，當只有流量超標情況下，發生風險的概率為0.018 8，而當增加一個風險因素，即流量、CPU都超標的情況下，發生風險的概率為0.026 0。由此可見，當更多的不利因素呈現時，網絡風險的概率就會增加。

1.2.4網絡風險評估通過對造成網絡風險主要因素的討論，給定一個參考系數，作為某個風險因素的概率變化的最大允許量[11]，表達如下：

其中，Xi是某個風險因素，i=1，2，3；RT表示發生網絡風險，RF表示沒有發生網絡風險，S是風險因素的狀態，u取T（True）或者F（False）。根據上文計算結果結合式（5）可以得到φ（X1）=76.07，φ（X2）=14.87，φ（X3）=21.56，即φ（X1）>φ（X3）>φ（X2） 。其中，X1、X2、X3分別代表流量、CPU、內存，φ越高則它造成網絡風險的可能性就越大。因此，由上述排序可知，在該段時間內，流量造成網絡風險的可能性最大，其次是內存，最后是CPU。得到流量、CPU、內存的后驗概率后，給定一個網絡風險率公式[11]如下：P（R）=P（L）×P（C）×P（M）〖JY〗（6）其中，P（L）、P（C）、P（M）分別表示在風險發生的情況下，是由流量引起的概率、是由CPU引起的概率以及是由內存引起的概率。將上文計算結果代入式（6）可得，P（R）=0.042 1。文獻[12]給出了風險頻率范圍的分類標準，如表6所示。由此可知：①網絡風險率結果顯示，該段時間的概率為0.042 1，屬于略高風險級別，需要加以重視；②由各網絡風險因素的影響程度可知，該時刻流量對網絡的影響程度最大，因此，需要對流量進行重點監控，必要時可進行限制。

2結語

本文主要研究了基于貝葉斯網絡方法的網絡風險評估問題，提出了相應的計算模型，并進行了實例計算。風險評估的過程主要包括風險識別、模型構造、定量計算。本文利用貝葉斯的條件獨立性假設這一特性，簡化了模型的計算復雜度，具有一定的應用價值。

參考文獻：

[1]孫鵬程，陳吉寧.基于貝葉斯網絡的河流突發性水質污染事故風險評估[J].環境科學，2009，30（1）：4751.

[2]吳欣.基于改進貝葉斯網絡方法的電力系統故障診斷研究[D].杭州：浙江大學，2005.

[3]閆峰.基于攻擊圖的網絡安全風險評估技術研究[D].長春：吉林大學，2014.

[4]S KONDAKCI.Network security risk assessment using bayesian belief networks[C].IEEE Second International Conference on Social Computing，2010：952960.

[5]TT CHEN，SS LEU.Fall risk assessment of cantilever bridge projects using Bayesian network[J].Safety Science，2014，70（70）：161171.

[6]S BARUA，X GAO，H PASMAN，et al.Bayesian network based dynamic operational risk assessment[J].Journal of Loss Prevention in the Process Industries，2015（41）：399410.

[7]WANG L，WANG B，PENG Y.Research the information security risk assessment technique based on Bayesian network[C].International Conference on Advanced Computer Theory and Engineering，2010：600604.

[8]楊嶸，張國清，韋衛，等.基于NetFlow流量分析的網絡攻擊行為發現[J].計算機工程， 2005，31（13）：137139.

[9]孫知信，唐益慰，張偉，等.基于特征聚類的路由器異常流量過濾算法[J].軟件學報，2006，17（2）：295304.

[10]李小爽.IP網流量流向分析及異常流量監控的研究[D].北京：北京郵電大學，2008.

[11]WANG X，ZHU J，MA F，et al.Bayesian networkbased risk assessment for hazmat transportation on the middle route of the SouthtoNorth water transfer project in China[J].Stochastic Environmental Research and Risk Assessment，2016，30（3）：841857.

[12]ESKESEN S D，TENGBORG P，KAMPMANN J，et al.Guidelines for tunnelling risk management：international tunnelling association， working group No.2[J].Tunnelling & Underground Space Technology，2004，19（3）：217237.

（責任編輯：孫娟）