輔助函數的應用
——基于懲罰函數的實證研究

郭蓉 段玉潔（通訊作者）

濟南大學

輔助函數的應用
——基于懲罰函數的實證研究

郭蓉 段玉潔（通訊作者）

濟南大學

本文主要通過查詢各種書籍及相關資料，介紹了輔助函數——懲罰函數的應用。懲罰函數的提出更好的解決規劃問題。本文希望通過輔助函數的詳細介紹來說明在數學領域中，輔助函數的重要性和廣泛應用，輔助函數并不是一個固定的函數，他是針對具體問題所提出的與題目相關的函數，對題目的解決具有非常關鍵的作用，希望大家能夠積極運用輔助函數來解決題目。

懲罰函數 非線性規劃 輔助函數

一、研究背景

解決數學問題經常用到函數，構造輔助函數來解決數學問題是一種極其有效的方法。構造輔助函數經歷了直覺數學、算法數學和現代構造數學三個階段。上世紀六十年代，比肖泊提出了“現代構造數學”的說法，他否定了直覺數學階段，擺脫了具有復雜理論的算法數學階段，超脫了各種束縛，并使用了極為簡單的符號的用語，容易被一般人看懂并理解。

二、研究目的和意義

當突然面對一個問題發現毫無頭緒并不能解決時，可從題目中所給的已知條件和待證結論的特點來構造輔助函數，再畫出函數圖像，通過圖像看出函數的奇偶性、單調性，解決完這個輔助問題，用這個輔助問題來推導出要解決的問題。輔助函數起到橋梁的作用，他將我們所知的條件構造出輔助函數與所證函數聯系起來進一步推導得出。

三、實證研究

（一）理論介紹

考慮一般約束最優化問題：

本章所講的懲罰函數的基本思想是：根據原問題中的約束條件設出目標函數，然后添加懲罰項得到帶參數的目標函數，我們對所要解決的約束問題就可以變為解決一系列的無約束非線性問題，也稱為序列無約束極小化技術。

（二）懲罰函數的應用

1.求解非線性規劃[1]

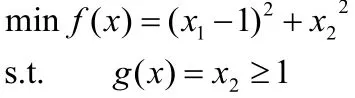
定義懲罰函數：

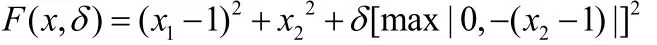
用解析法求解minF(x,δ)，有：

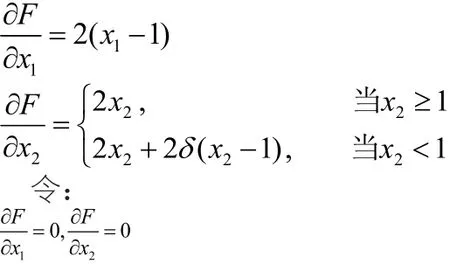
得到：

2.飲料的生產批量問題[2]

某飲料廠有一條生產線，并用該生產線輪流生產多種飲料，某周開始生產一種飲料，需要6千元的生產準備費。其中生產成本：100元/箱；貯存費：每周每千箱飲料2千元。該飲料前4周的需求量如下表所示，應該如何安排生產，使其既能滿足要求的生產量又能使4周的總費用最小。由已知可得：

目標函數：

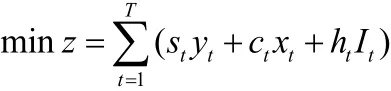
約束條件：

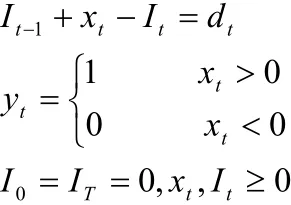
其中，ct為時段t 生產費用(元/件)，ht為時段t 庫存費 ，st為時段t 生產準備（元）dt為時段t 市場需求（件），xt為時段t生產量，It為時段t 庫存量，yt=1為時段t開工生產，yt=0為不開工。

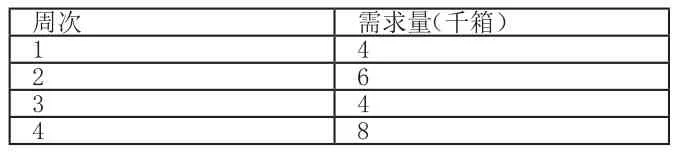
周次需求量（千箱）1 4 2 6 3 4 4 8

合計22

構造罰函數I(yt)=Myt(e?yt)，約束問題轉化為，為下列模型：

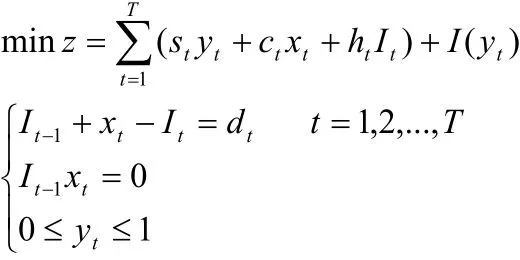
求解該非線性規劃得出最優解x=(4,10,0,8)。

四、結論

我們通過查閱資料及相關文獻可知，懲罰函數法是一種使用很廣泛，很有效的輔助函數法。它在不破壞原約束的約束條件下，將最優解歸結到原約束問題的最優解上面去。我們發現懲罰函數法在現實生活應用中，可以把約束優化問題轉化為無約束優化問題來求解，具有更強的適用性。

[1]施光燕,龐麗萍.最優化方法[M].北京: 高等教育出版社,2007.8：81-86

[2]王興華.懲罰函數法的改進算法及應用研究[D].燕山大學,2009.

郭蓉（1996-），山東菏澤人，濟南大學數學科學學院本科在讀；通訊作者：段玉潔（1996-），山東菏澤人，濟南大學數學科學學院本科在讀。