以運輸時間最小為目標的物流運輸調度問題研究

宗仁 浙江理工大學

以運輸時間最小為目標的物流運輸調度問題研究

宗仁 浙江理工大學

物流運輸調度問題是一類求解難度較高的運輸問題，在制定合理的調度方案時，實現物流運輸時間最小對于一些要求最快時間運送的加急服務是一件迫切需要解決的問題。文章分析了調度問題的特點，建立了以物流運輸時間最小為目標函數的物流運輸調度模型，并且通過給出合理的計算方法，得到物流運輸時間最小的調度方案，驗證了模型的可行性和算法的有效性。

運輸時間最小 車輛調度

一、引言

近年來，由于電商的發展，物流運輸的時間已經成為顧客對于網上購物體驗的重要影響因素，各家物流企業在物流時間上的競爭日漸激烈，先有京東推出211限時達，之后阿里巴巴牽頭的‘菜物’物流成立，目標通過5至8年的努力打造一個開放的社會化物流大平臺，在全國任意一個地區做到24小時送達。以上這些都體現了時間對于物流運輸巨大的影響。減少運輸時間不僅可以提高運輸效率，也可以提升企業的服務水平。

企業物流配送系統中若干定位路徑問題的建模與調度方法_趙志彥[1]分別利用了啟發式算法和精確算法，對配送中心選址以及出入庫路徑選擇進行了分析，以成本和時間作為主要評價標準，對于LRP問題進行研究優化。基于工作流網的交通應急資源配置和路徑規劃集成問題_袁飛[2]對于交通應急規劃做了統籌的調度解答，但是這種模型主要應用于一個多部門多方面合作的應急網絡中，并不適合于末端物流配送中心的日常配送。帶時間窗的聯盟運輸調度問題蟻群算法研究_師凱[3]主要研究了在規定時間內由單個或是多個配送中心分配最佳的運送方式達到運輸總成本最小，該模型中利用車隊尋找最優路線達到車隊總費用最低，但是這種方式靈活度不高，不能同時滿足各個運送點的運送需求，雖然降低了總體費用，但是無法在最快時間下將車輛從工作中解脫出來再利用，完成周期性最短時間的運送任務。

文章分析了某物流企業調度中心物流運輸調度問題的特點，建立了以物流時間最小為目標函數的物流運輸調度模型。然后利用適合的算法進行求解，得到了物流運輸總時間最小的調度方案，提高物流中心調度效率，提高物流公司的持續性運送能力，減少物流企業在運輸中因車輛調度不合理所造成的浪費，從而提升了企業效益[4-6]。

二、物流運輸問題描述

物流運輸調度問題中，經常發生特殊情況需要對特定的數個運輸點進行即時運輸，由于運輸地點之間的距離差、各需求方需求量不同、運輸時道路狀況不同以及運輸車輛本身差異，調度中心如果無法根據各種影響因素制定合適的調度方案，實現最小運輸時間，輕則可能喪失訂單，重則可能影響企業發展。

動態規劃方法是現代企業高效管理的一種重要決策方法，物流企業的調度是連續進行的，將這個連續的過程根據執行配送的調度方案劃分為若干個相互聯系的階段，在每個階段執行一個調度方案，這些相互聯系的調度過程可以反映整個物流運輸調度決策。整個決策過程的目標是達到物流運輸時間最小，因此使用動態規劃的方式更加適合物流運輸調度，將動態規劃方法應用于物流運輸問題，將物流調度問題分為不同的階段，然后獨立處理不同階段，最終得出使整個運輸時間最小的調度方案。

假設某物流配送中心需要向K個物流自提點運送貨物，各點的需求量tk，各點間間距，設i為車型現共有N種車型，j為車數量每種車型n輛，各種車型載重量Xi，各種車型的運輸速度為Vi，各種車型可實現運輸路線Yim，F為某一配送路線情況下下給個點的運輸量。某一配送路線情況下運輸時間為T。

前提假設：貨車到達某一需求點時會優先滿足該點的所有需求量，在滿足該點的需求量的前提下再去下一個運輸點，當貨車貨物量為零或是整個運輸網絡中各點的需求量都已滿足時貨車返回配送中心。

注：A為k行一列的矩陣，矩陣中的數值隨機取1或0。Ak和Ak-1的k-1行相同。

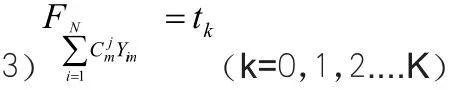
（1）是為了使選擇的車輛的總載重量大于各點需求總量

（2）是為了得到每種車型的可能運輸路線，車型的路線選擇時，既要滿足將該車的所有貨物卸下又要滿足在所有貨物卸下后不再向下一個運輸點運送。

根據公司需求，除了要滿足單次最小運輸時間，還需要保留一部分運輸能力以保證應急運輸，所以當利用以上模型求解出最小時間的運輸分配任務之后，還需要從結果中篩選出合適的運輸能力的方案，這個篩選會根據公司的實際需求來決定，文章就不再一一展開說明。

三、求解物流運輸調度問題

在這個問題中我們需要求出最佳的車輛分配，以及對應的路線選擇。（1）對于這個問題我們由于限制條件的作用，我們可以先根據整個運輸網絡中的需求量求出所需的各種類型的貨車數量；（2）根據每種類型的車輛的載重量，可以求出每種車能夠完成的配送路徑；（3）將第一步中每一種情況下的貨車在第二步中隨機選擇路徑，判斷該路徑下是否可以滿足各自提點的需求量，如果滿足繼續往下；（4）計算每種情況下的完成該任務所需時間，記為最小時間，與下一個情況的時間進行比較，取兩者中的最小值，循環直到求出第一步中的一種情況下的最小時間；（5）對第一步中的各個情況進行比較，尋求最優的車輛需求量以及盡量最小的時間。求解模型如下圖（2）：

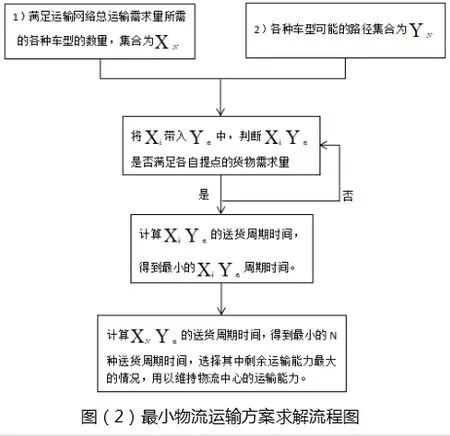
四、案例分析

文章以A物流中心為例，建立了物流運輸調度模型。該公司需要在最短時間內完成貨物運送，并且返回調度中心以供接下來的調度作業，另外由于公司需要保證有應急調度能力，需要保留一定量的調度能力，本次案例中的保留調度量假設與當前運送量相當。公司共有三種車型，分別為M1,M2,M3，每種車型各三輛貨車，每種運輸車速度載重量一定，M1：載重量10T、車速80km/h，M2：載重量20T、車速70km/h，M3：載重量30T、車速50km/h。現在B、C、D、E四個需求點需求量分別為：20T、10T、25T、25T。 四點間的路程距離如圖（3）

總運輸網絡需求量80T，M1,M2,M3的數值按照隨機數列進行篩選：

M1,M2,M3三種類型的車子可能的路線：

M1,M2,M3三種類型的車子選擇上表路線時所需經過的路程：

當只有三輛M3參加運輸時最優解：A-D,A-E,A-B-C最小時間1.2h。

同理可以求出其他狀態下的最優解，將此結果作為參考項，可以使物流中心的運輸達到最快時間并且仍然擁有所需要的運輸能力，并且可以根據這樣的運算方式做一份周期性的持續性的快速運輸方案，使運輸效率大幅度提高，也使物流企業始終保持一定的物流能力。

五、結束語

文章研究了在有限的物流運輸能力下，如何做到最快速運輸并且維持一定的應急物流運輸能力。使用的方法是將數據輸入對應相應運算程序的方法，雖然運算量巨大，但是可以較為精確的計算最小時間，有利于實際運送中提前規劃安排運送任務。文章的不足之處是沒有做到更精確的物流數量運送，即無法做到某車在各需求點各放下多少貨物來更進一步計算更精確的最小時間，解決方法其實是可以用向量假設，假設每一個運送點的運送量，讓后進行計算，不過考慮到在實際中這樣做并不會有太大意義，所以以此條件作為限制。

[1]趙志彥, 企業物流配送系統中若干定位—路徑問題的建模與調度方法, 2009, 天津大學. 第 129頁.

[2]袁飛, 基于工作流網的交通應急資源配置和路徑規劃集成問題, 2015, 廣東工業大學. 第 66頁.

[3]師凱, 帶時間窗的聯盟運輸調度問題蟻群算法研究, 2006, 廣東工業大學. 第 69頁.

[4]張國輝與黨世杰, 基于匈牙利算法的物流運輸調度問題研究. 物流技術, 2016(01): 第117-119頁.

[5]成榕與吳先鋒, 最小時間路徑算法模糊結構元改進. 遼寧工程技術大學學報(自然科學版), 2014(05): 第683-686頁.

[6]欒琨, 基于規則的出行路徑和出發時間選擇行為研究, 2013, 吉林大學. 第 129頁.

宗仁（1992.09.27-），男，江蘇常熟籍，碩士在讀學歷，浙江理工大學，專業：物流工程。