NSD隨機變量和的單邊概率不等式
蔡 婷,熊 彪
(湖北師范大學數學與統計學院,湖北 黃石 435002)
NSD隨機變量和的單邊概率不等式
蔡 婷,熊 彪
(湖北師范大學數學與統計學院,湖北 黃石 435002)
主要利用Fuc-Nagaev型概率不等式的方法去研究負超可加相依NSD(negatively superadditive dependent)隨機變量和的單邊概率不等式.利用這種方法,得到了一些重要的大偏差概率不等式.所得結果推廣了獨立隨機變量和NA隨機序列的相應結果.
超可加函數;NSD隨機變量;大偏差概率不等式
0 引言
自20世紀50年代起,有很多概率統計學者相繼提出了混合變量和相依變量的概念,例如ρ—混合變量[1]、φ—混合變量[1]、負相協(NA)變量[2]、負超可加相依(negatively superadditive dependent,NSD)變量[3]等.在眾多相依變量中,NSD隨機變量是概率統計學者們最感興趣的相依變量之一.NSD隨機變量的概念由文獻[3]引入的,它是建立在超可加函數的基礎上.下面給出超可加函數的概念.
定義1[3]函數Φ:Rn→R稱為超可加的,如果對任意的x,y∈Rn有
Φ(x∨y)+Φ(x∧y)≥Φ(x)+Φ(y),
其中,“∨”表示兩者之間的最大值,“∧”表示兩者之間的最小值.
在超可加函數的基礎上,文獻[3]提出了NSD隨機變量的概念,具體如下:
定義2[3]隨機向量X=(X1,X2…,Xn)為負超可加相依的(NSD),如果滿足
Eφ(X1,X2,…,Xn)≤Eφ(Y1,Y2,…,Yn)
其中φ(·)是超可加函數,Y1,Y2,…,Yn相互獨立,且對任意的i,Xi和Yi同分布,稱隨機變量序列{Xn,n≥1}是NSD的.
國內外對NSD隨機變量的研究很多,許多統計學家對NSD隨機變量的研究產生了興趣,一系列有用的結果相繼被提出.至今為止,對于NSD變量的研究已經取得了很多有意義的結果.例如:在文獻[4]中, Nagaev S V得到關于獨立同分布的隨機變量X1,…,Xn的和的概率不等式.文獻[3]舉例說明NSD并不能推出負相協(NA),等等.本文研究了比NA序列更為嚴格的NSD序列,得到了NSD隨機變量和的單邊不等式,同時也推廣了已有文獻HU[3]、FUK[4]以及SU[5]等的相關結論.
1 主要結果
本節我們將得到NSD序列在特殊條件下關于最大部分和具有NSD特色的Fuk-Nagaev型單邊概率不等式,并與獨立隨機變量、NA隨機變量這兩類隨機變量進行比較,發現它們具有類似的性質,由此可以推斷出兩類隨機變量與NSD在其它性質上也會有相似之處.
為了結果的需要,首先給出以下引理.
引理1[4]設X1,…,Xn是獨立同分布的隨機變量,且滿足EX1=0,DX1=1,則
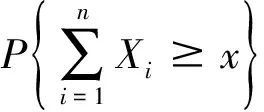

下面應用引理1對NSD隨機變量序列建立了以下的大偏差概率不等式.
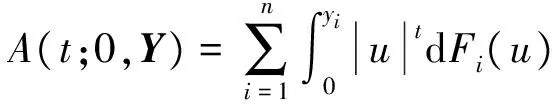
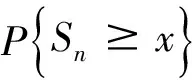
(1)
其中
(2)
若xyt-1>A(t;0,Y),則有
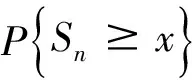
(3)
其中
(4)
并且P2≤P1.
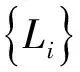
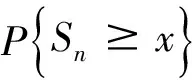
證明 由于滿足定理1的條件,則有(1)、(2)式成立. 取yi=Li,i=1,2,…,n且y=L=
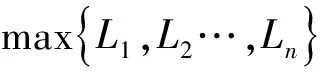
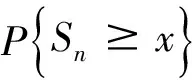
由定理1的證法及(2)式可得推論1. 在此略.

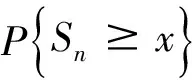
證明 推論2的證明與推論1的證明類似,在此略.
注1 推論1~2 給出了在隨機變量序列有界的情況下NSD隨機變量序列關于部分和Sn的概率不等式.將NSD隨機變量和的概率不等式的復雜形式變得簡單化.
注2 推論1與文獻[6]中獨立隨機變量序列的最大部分和概率不等式的結果相比,除了常數的差別外,其余形式完全相同;注意到文獻[7]中定理1建立了NA隨機序列部分和的概率不等式與這里的推論1 也是有常數的差別,而在獨立隨機變量場合中二者卻完全相同.
綜上所述,對獨立隨機變量序列及NA隨機變量序列上述類似的不等式成立.由此表明,NSD隨機變量序列既有與獨立隨機變量及NA隨機變量類似的極限性質,又有其特色之處.
2 主要結果的證明
為了證明本文的主要結果,需要用到以下引理,具體可參考文獻[3].
引理2[3]如果隨機變量(X1,X2,…,Xn)是NSD的,且g1,g2,…,gn都是非降函數,則(g1(X1),g2(X2),…,gn(Xn))也是NSD隨機變量.
定理1的證明 設X1,X2,…,Xn是NSD隨機變量,Z1,…,Zn是獨立的隨機變量,且Xi與Zi同分布.令
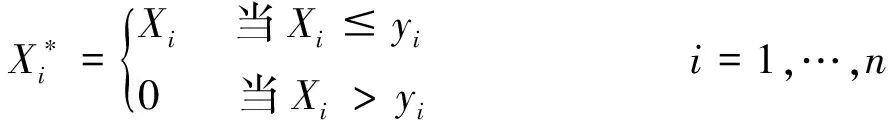
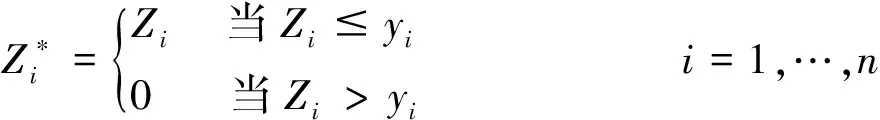
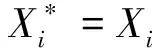
令
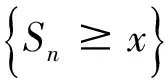
因此
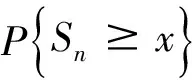
(5)
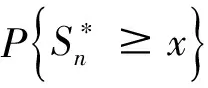
根據(5)式,我們得到
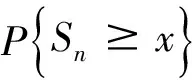
(6)
現在,我們在證明這個定理的本質上是對不等式(6)右邊第二項進行討論.
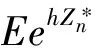


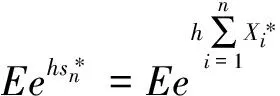
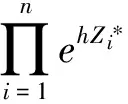
因此

(7)
令
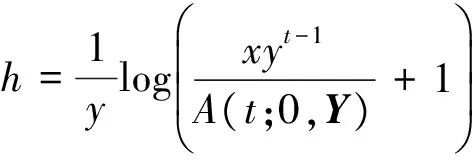

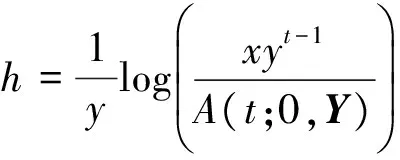
得到(7)式的右式的最小值.當h滿足xyt-1>A(t;0,Y)式條件時,將其h代入(7)式,可以得出

其中P2是通過(5)式得到的. 結合(6)式可以得到(4)式.顯然,P2≤P1.
至此,定理1證明完畢.
[1]吳群英. 混合序列的概率極限理論[M]. 北京:科學出版社,2006.
[2]Joag-Dev K, Proschan F. Negative association of random variables with applications [J]. The Annals of Statistics, 1983, 11(1): 286~295.
[3]Hu T Z. Negatively superadditive dependence of random variables with applications[J]. Chinese Journal of Applied probability and Statistics , 2000, 16: 133~144.
[4]Fuk D Kh, Nagaev S V. Probability inequalities for sums of independent random variables[J]. Theory of Probability and Its Applications, 1971, 16: 643~660.
[5]蘇 淳, 趙林城, 王岳寶. NA序列的矩不等式與弱收斂. 中國科學, A輯, 1996, 26(12): 1091~1099.
[6]Su C, Zhao L C, Wang Y B. Moment inequalities and weak convergence for negatively associated sequence[J]. Science in China Ser A, 1997, 40(2) : 172~182.
[7]Shao Q M. A comparison theorem on maximal inequalities between negatively associated and independent random variables [J]. Journal of Theoretical Probability, 2000, 13(2): 343~356.
Unilateral probability inequalities for sum of negativelysuperadditive dependent random variables
CAI Ting,XIONG Biao
( College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002,China)
Using the Fuc-Nagaev type probability inequality, we mainly study the unilateral probability inequalities for sum of negatively superadditive dependent random variables. By using this method ,we obtain some important large deviation probability inequality. The results generalize some corresponding ones for independent random variables and some negatively dependent random variables.
superadditive function; negatively superadditive dependent random variable; large deviation probabilities inequalitie
2016—11—11
國家自然科學基金(11471105),湖北師范大學科研團隊(T201505)
蔡婷(1991— ),女,湖北荊州人,碩士研究生,主要研究方向為概率論與數理統計.
O211.5
A
2096-3149(2017)02- 0053-04
10.3969/j.issn.2096-3149.2017.02.012

