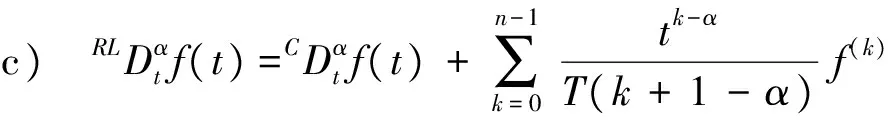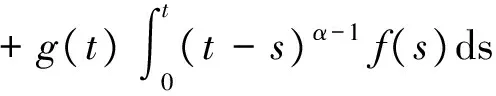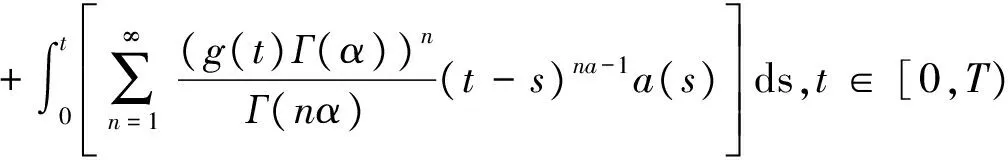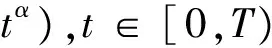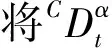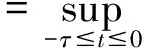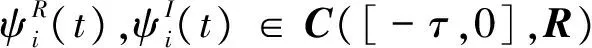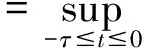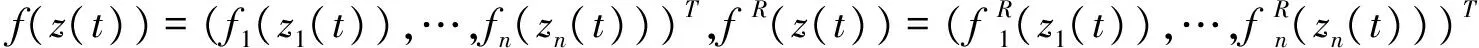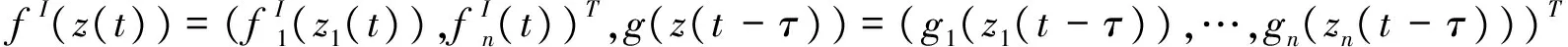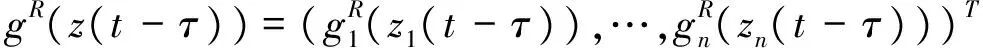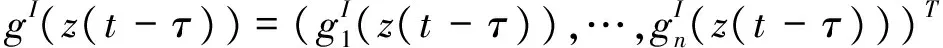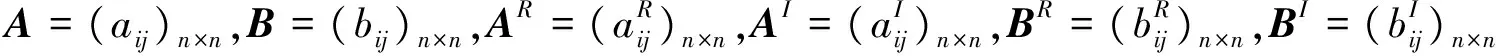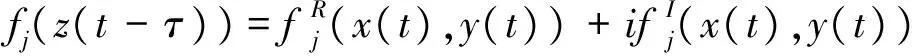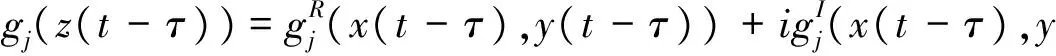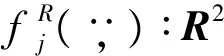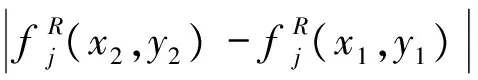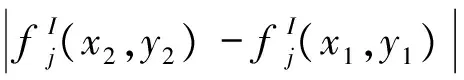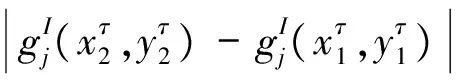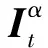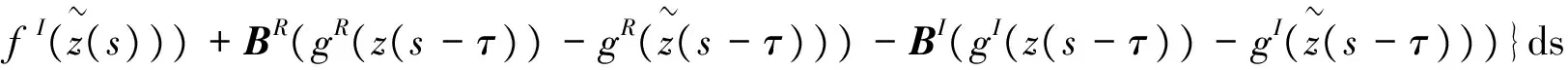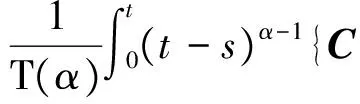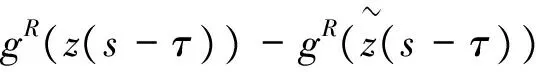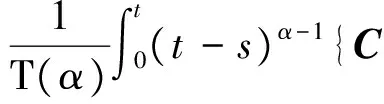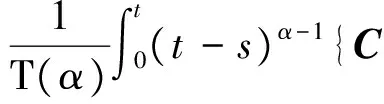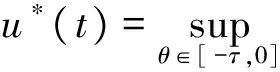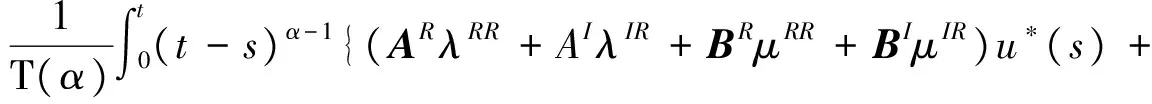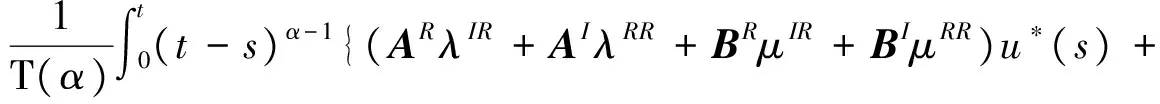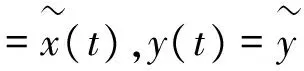一類帶有時滯的復值分數階神經網絡的解的唯一性

鐘 杰，陳伯山，尹 婷，劉 玲，吳尹哲

(湖北師范大學 數學與統計學院，湖北 黃石 435000)

一類帶有時滯的復值分數階神經網絡的解的唯一性

鐘 杰，陳伯山，尹 婷，劉 玲，吳尹哲

(湖北師范大學 數學與統計學院，湖北 黃石 435000)

主要研究一類帶有時滯的復值分數階神經網絡的解的唯一性。通過運用Mittag-Leffler函數和推廣的Gronwall不等式得到系統解唯一的充分條件。

復值；分數階；神經網絡；時滯；唯一性

作為一種特定的動力系統，神經動力學系統是近些年來研究的一個熱門問題。我們看到的大部分系統，是整數階神經動力系統，而現實生活中的例子，要求系統是任意階的，所以，研究分數階系統很有應用價值。分數階微積分在物理和工程方面有著廣泛的應用[1～4]。在[3]中，陳潔潔等研究了一類基于憶阻分數階神經網絡的全局Mittag-Leffler穩定和同步。考慮到時滯的影響，在[4]中，作者研究了一類帶有時滯的非自治分數階神經網絡的全局穩定性和全局漸進周期性。

復值神經網絡是實值神經網絡的延伸，在復值神經網路中，狀態變量，連接權，激活函數為復值函數。它廣泛地應用于信號處理，通信工程，醫學成像等。復值神經網絡能解決實值神經網絡不能解決的問題，近幾年來，復值分數階神經網絡的研究有了很大的進展[5～6]。例如，在[5]中，作者研究了一類帶有時滯的基于憶阻復值分數階神經網絡的有限時間穩定問題。

定義1[1]一個連續函數f(t)的α階分數階積分定義如下：

(1)

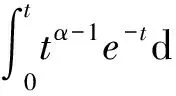
定義2[1]一個連續函數的階Riemann-Liouvile分數階導數定義如下：

(2)

其中，t>0，α>0，n是一個正整數，α滿足n-1<α

定義3[1]一個連續函數f(t)的α階Caputo分數階導數定義如下：

(3)

其中，t>0，α>0，n是一個正整數，α滿足n-1<α

定義4[2]Mittag-Leffler函數定義如下：

(4)

其中，α>0，z∈C，C表示復數。

帶有兩個參數的Mittag-Leffler函數有如下形式：

(5)

其中，α>0，β>0，z∈C，當β=1時，有Eα(z)=Eα,1(z)，而且E1,1(z)=ez.

引理1[3]如果f(t)∈Cn[0,+∞)及n-1<α

引理2[4]f(t),a(t)在(t≤∞)上是局部可積的非負函數。g(t)是定義在0≤t≤T上的非負且單調不減的函數，且g(t)≤M，M為常數，若

(6)

則有

(7)

而且，a(t)在[0,T)上是一個單調不減的函數，則

(8)

其中，Eα(·)是帶有一個參數的Mittag-Leffler函數。

考慮由下面的微分方程描述的一類分數階復值神經網絡：

(9)

其中，t≥0，i=1，…，n，n表示神經系統神經元的個數，zi(t)表示第i個神經元相關的復值狀態變化；ci>0，它是一個常數，aij(t)和bij(t)分別表示第j個神經元在時間t和t-τ處對第i個神經元的復值加強。fj(zj(t))和gj(zj(t-τ))分別表示第j個神經元在時間t和t-τ處對第i個神經元的復值激活函數。

與系統相關的初始條件有如下形式：

(10)

現將(9)式寫成實部和虛部兩部分。令

(11)

(12)

與(10)式相關的初始條件有如下形式：

現將系統(9)，(11)，(12)轉化成向量形式如下：

(13)

(14)

(15)

其中，z(t)=(z1(t),…，zn(t))T，x(t)=(x1(t)，…，xn(t))T,y(t)=(y1(t),…yn(t))T,

在這部分，應用Mittag-Leffler函數及推廣的Gronwall不等式證明復值分數階系統的解的唯一性。

假設1 令z=x+iy，其中i表示虛數單位，i2=-1，fj(z(t)和gj(z(t-τ))可以寫作：

為了方便，將x(t-τ)，y(t-τ)分別記作xτ，yτ.

(16)

(17)

這樣，根據多元函數的微分中值定理，得到對任意的x1，x2，y1，y2，有

(18)

定理1 如果z∶[-τ，T]→Cn是一個連續的可微函數，稱z(t)是系統(13)滿足初值條件z(t)=ψ(t)，-τ≤t≤0的解當且僅當

證明 首先證明必要性。設z(t)是系統(13)滿足初值條件z(t)=ψ(t)，-τ≤t≤0的解，

則

Dαz(t)=≡-Cz(t)+Af(z(t))+Bg(z(t-τ))+I

由(10)式知 ，當-τ≤t≤0時，z(t)=ψ(t) .

(19)

由引理1得到

(20)

則系統(13)解的形式如下：

(21)

現在證明充分性。設

對上式兩邊求階Caputo分數階導數，得

Dαz(t)=-Cz(t)+Af(z(t))+Bg(z(t-τ))+I

顯然,z(t)=ψ(0)，-τ≤t≤0。證畢。

定理2 若假設1成立，則系統(13)至多有一個解。

當0≤t≤T時，令

由(21)式得到：

(22)

(23)

(24)

BR[μRR‖u(s-τ)‖+μRI‖v(s-τ)‖]+BI[μIR‖u(s-τ)‖+μII‖v(s-τ)‖]}ds≤

(25)

(26)

同理得到：

(27)

(28)

令h(t)=(AR+AI)(λIR+λRR)+(BR+BI)(μIR+μRR)

k(t)=(AR+AI)(λRI+λII)+(BR+BI)(μRI+μII)

m(t)=max{h(t),k(t)}

對任何ε>0，我們有

根據引理2，

(29)

這就完成了定理2的證明。

本文研究了一類帶有時滯的復值分數階神經網絡的解的唯一性，應用了Mittag-Leffler函數和推廣的Gronwall不等式。在復值分數階神經網路研究領域，可以做進一步的研究，如復值分數階神經網絡的動力學分析。

[1]Podlubny I. Fractional differential equations[M]. Academic Press, New York, 1991.

[2]Chen J, Zeng Z, Jiang P. Mittag-Leffler stability and synchronization neural networks[J]. Neural Networks. 2014, 51: 1～8.

[3]Chen B, Chen J. Global O() stability and global asymptotional for a non-autonous fractional-order networks with time-varying delays[J]. Neural Networks the Official Joumal of the International Neural Society, 2016, 73: 47～57.

[4]Ye H, Gao J, Ding Y. A generalized Gronwall inequality and its qpplication to fractional defferential equation[J]. Math. Appl. 328, 2014, 1075～1081.

[5]Rakkiyappan R, Velmurugan G, Cao J. Finite-time stability analysis of fractional-order complex-valued memristor-based neral networks with time delays[J]. Nonlinear Dynamics, 2014, 78(4): 2813～2836.

[6]Xu X, Zhang J, Shi J. Exponential stability of complex-valued neural networks with mixed delays[J]. Neurocomputing 128, 2014, 483～490.

The uniqueness theorem of the solution to a class of fractional-ordercomplex-valued neural networks with time delays

ZHONG Jie, CHEN Bo-Shan, YIN Ting, LIU Ling, WU Yin-Zhe

(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435000, China)

The present paper studies the uniqueness theorem of the solution to a class of fractional-order complex-valued neural networks with time delays.Using Mittag-Leffler functions and generalized Gronwall inequality, some sufficient conditions are derived to guarantee The uniqueness theorem of the solution to the system.

fractional-order; complex-valued; time delays; uniqueness

2016—06—20

鐘杰(1991— )，女，湖北十堰人，碩士研究生，主要研究方向為分數階微分方程.

O175

A

2096-3149(2017)02- 0057-05

10.3969/j.issn.2096-3149.2017.02.013