夾層復合材料圓柱殼表層的纏繞優化

陳 悅 李華東 朱 錫 朱子旭

(1 海軍工程大學勤務學院，天津 300450)(2 海軍工程大學艦船工程系，武漢 430033)

夾層復合材料圓柱殼表層的纏繞優化

陳 悅1李華東2朱 錫2朱子旭2

(1 海軍工程大學勤務學院，天津 300450)(2 海軍工程大學艦船工程系，武漢 430033)

文 摘 以平衡型穩定網絡為約束條件，以等強度和提高臨界失穩載荷為設計目標，對夾層復合材料圓柱殼體的纏繞表層進行了優化研究。首先，基于等強度設計，得到表層的最優纏繞方式為螺旋加環型纏繞，且螺旋纏繞角應滿足α≤54.7°；其次，以結構強度及穩定性為雙重指標，采用ABAQUS建立有限元模型，求解不同長徑比的夾層復合材料圓柱殼的最優螺旋纏繞角αopt。研究發現：當長徑比0.5≤η≤3時，隨η增加，表層的最優纏繞方式從單一螺旋加環型纏繞過渡至縱向鋪放加環向纏繞，且最大臨界失穩載荷Pcr近似呈二次遞減關系。該優化方法不僅可達到輕量化要求，而且滿足結構強度和穩定性雙重指標。

復合材料，纏繞，夾層圓柱殼，優化

Abastract Based on the balanced stable network as constraint conditions, with equal strength designing and improving the critical buckling load as the design goals, wound surface of sandwich composite cylinder was optimized. Firstly, based on equal strength design method, the optimal winding pattern and winding angles of spiral winding were obtained.The winding angle should satisfyα≤54.7°.Secondly, in order to meet the need of structural strength and stability, stability models with different aspect ratio are established using ABAQUS finite element software to obtain theαopt.The study has found that when the aspect ratio 0.5≤η≤3, with the increase ofη, the best way transited from a single wound spiral wound ring plus hoop wound to the longitudinal placement plus hoop wound, while the maximum critical buckling load is approximately decreasing in quadratic relationship. The optimization method can not only achieve weight reduction requirements, but also meet the dual indicators of structural strength and stability.

0 引言

夾層復合材料圓柱殼廣泛應用于航空航天、海洋等領域，其表層蒙皮常采用纏繞成型，形成平衡型網絡結構，以利于發揮纖維的縱向強度。國內外對纏繞復合材料圓柱殼開展的相關研究有：基于網絡理論，陳汝訓[1]推導了纖維纏繞殼體圓筒壁厚和爆破壓強的理論解，與試驗結果吻合良好；譚三五[2]開發了纖維纏繞殼體可靠性數字仿真方法及程序；胡寬[3]以殼體質量為目標，利用線性多步法和復形調優法，優化設計固體發動機纖維殼體，指出比強度是影響纖維殼體質量的最重要因素；欒宇[4]采用蟻群算法(ACA)對纏繞層順序進行優化，并開發纏繞復合材料殼體鋪層順序優化程序系統，實現殼體結構的穩定性優化設計；祖磊[5]基于薄膜理論和網絡理論，給出均衡纏繞線型的確定方法，并利用序列二次規劃算法(SQP)求得不同爆破壓強下各項最優均衡纏繞參數；Cheol-Ung Kim[6]考慮了纖維與心軸表面滑動及纏繞工藝的可靠性，采用半最短曲率路徑算法，對內壓容器的纏繞方式進行優化。

目前大部分優化設計均為滿足殼體強度前提下，達到質量最輕化，或以提高極限承載、爆破壓力為優化目標，較少考慮結構穩定性問題。本文以夾層復合材料圓柱殼的纏繞表層為研究對象，首先基于網絡理論，以平衡型穩定纏繞為約束，依據等強度設計理念，得到表層纏繞方式和纏繞角度的優化解；其次，采用ABAQUS有限元軟件，建立結構穩定性計算模型，以提高臨界失穩載荷為優化目標，求解滿足結構強度及穩定性的最優纏繞方式及纏繞角度。

1 基于等強度和穩定性的設計方法

1.1 設計思路

纖維纏繞的主要網絡單元有4種，即單一螺旋型、螺旋加環型、螺旋加縱向型、縱向加環型，考慮到工程應用條件，本文僅對單一螺旋纏繞和螺旋加環型兩種纏繞方式進行最優化設計。

設計分兩步走：第一步，基于平衡型網絡理論，以等強度設計為目標，得到滿足結構強度要求的纏繞方式、纏繞層厚度、纏繞角度等參數，此時對應的結果并非唯一解；第二步，在滿足等強度設計的基礎上，采用有限元軟件，建立結構穩定性計算模型，以提高最大臨界失穩載荷為目標，得到同時滿足結構強度及穩定性要求的最優解，具體流程見圖1。

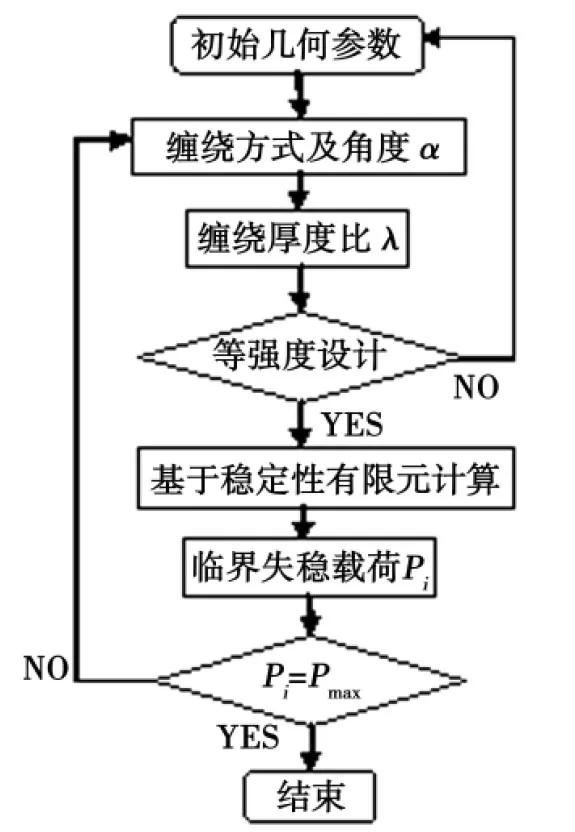
圖1 圓柱殼體表層最優纏繞設計流程

1.2 實施步驟

對于均勻靜水壓力載荷作用下，采用螺旋加環向纏繞的復合材料夾層耐壓圓柱殼，設螺旋纏繞角度為±α，環向纏繞角度為π/2。取殼體的軸向坐標為z，環向坐標為θ，分別平行于θ和z方向切取單位長度的網絡單元[8]。

由平衡方程得，圓柱殼體的軸向和環向薄膜內力為：

(1)

式中，R為圓柱殼體半徑，p為均布壓力的大小。

因芯材的模量遠遠低于表層碳纖維復合材料，忽略芯材對表層纖維應力的影響。當網絡單元處于平衡狀態時，則纖維張力與薄膜內力必須滿足如下關系：

(2)

式中,σfα為螺旋纏繞纖維應力,σfθ為環向纏繞纖維應力,hfα為螺旋纏繞纖維厚度,hfθ為環向纏繞纖維厚度。

平衡型應變狀態時，εfα=εfθ=ε，所以σfα=σfθ。此時式子(2)變為：

(3)

將式(3)中的兩式相除，得螺旋加環向纏繞網絡的平衡條件：

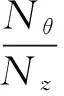
(4)

式中，λθz為環向纖維與螺旋向纖維厚度比。記內力比η=Nθ/Nz，由式(4)得纖維厚度比為：

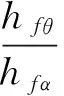
(5)

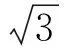
由等強度設計理論知，纖維所受的應力：

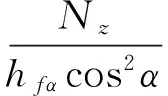
(6)

在靜水外壓p作用下的纖維應力為：

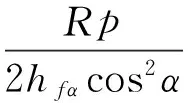
(7)

設纖維斷裂應力為σfb，設計的結構承載壓力為pb，則圓筒的螺旋纏繞纖維厚度為：

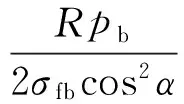
(8)

環向纏繞層厚度為：

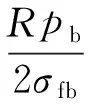
(9)

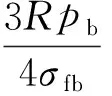
對于夾層復合材料圓柱殼體表層，以平衡型網絡結構為約束，考慮工藝可靠性，由等強度設計法得到的最優纏繞方式為螺旋加環型纏繞，纏繞角應滿足α≤54.7°，對應的螺旋纏繞和環向纏繞的厚度可由式(8)、式(9)確定。以上方法中，纏繞角α并非唯一解，其最優角度可通過穩定性分析進行確定。采用有限元軟件，建立結構穩定性計算模型，以提高最大臨界失穩載荷為目標，通過復形調優法，得到同時滿足結構強度及穩定性的最優纏繞方式及角度。

2 算例

某復合材料夾層圓柱殼直徑D=553 mm，表層復合材料體系為EM301樹脂及HF10-12K型T300碳纖維，采用濕法纏繞工藝成型，內外蒙皮各纏繞四層。由該材料體系制備單向板進行材料力學性能測試(表1)。芯層為高強浮體填充材料HW055，彈性模量為970 MPa，泊松比為0.3。

定義長徑比η=L/D，采用有限元軟件ABAQUS建立η=1、2、3的復合材料夾層圓柱殼結構模型(圖2)。芯層采用實體單元C3D8R模擬，表層采用連續殼單元SC8R模擬，模型底部約束軸向位移及兩個轉角的自由度(U3=UR1=UR2=0)，頂部采用MPC技術將頂部端面與參考點RF等效約束，同時約束軸向位移及三個轉角的自由度(U3=UR1=UR2=UR3=0)，施加均勻靜水外壓，頂部于MPC參考點施加等效軸向集中力載荷，邊界條件和載荷設計見圖3。

表1 表層材料HF10/EM301力學性能

圖2 夾層復合材料圓柱殼體模型(η=1，2，3)Fig.2 Finite models of sandwich composite cylinders with different η

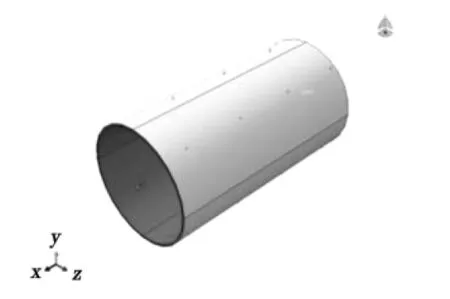
圖3 邊界條件與載荷設計

2.1 不同纏繞角度下的最優纏繞方式

對于螺旋加環向纏繞及單一螺旋纏繞復合材料圓柱殼，當纏繞角α≤54.7°時，結構滿足平衡型網絡要求。由式(8)、(9)，計算不同纏繞角α所對應的螺旋纏繞與環向纏繞厚度比例，如表2所示。

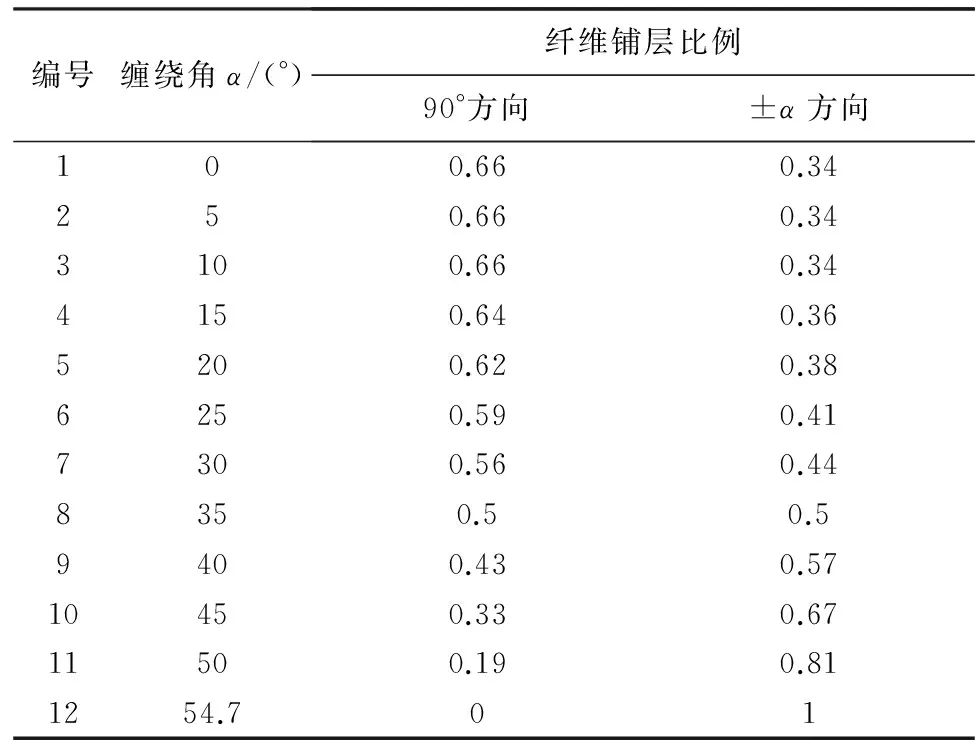
表2 不同纏繞角對應的纏繞方式

采用有限元軟件ABAQUS，建立結構穩定性計算模型，分別計算采用上述纏繞方式的復合材料圓柱殼在靜水外壓作用下的臨界失穩載荷，并繪制η=1，2，3的復合材料夾層圓柱殼失穩載荷pcr隨螺旋纏繞角αp的變化規律曲線(圖4)。由圖4可知：對于長徑比η=1，2，3的復合材料圓柱殼，最優化纏繞角度αp分別為50°、30°、0°。對于η=1圓柱殼，隨纏繞角度增加，最大臨界屈曲載荷也增加，故最優纏繞方式應接近于單一螺旋纏繞，αp=54.7°；對于η=3圓柱殼，隨纏繞角度增加，最大臨界失穩載荷呈下降趨勢，故最優纏繞方式應接近于縱向鋪放加環向纏繞，但此纏繞方式為工藝帶來難度，從耐壓圓柱殼體穩定性角度考慮，建議圓柱殼體長徑比不宜過大，當長徑比較大時，需考慮增加艙壁或肋骨以便于纏繞工藝的實施。

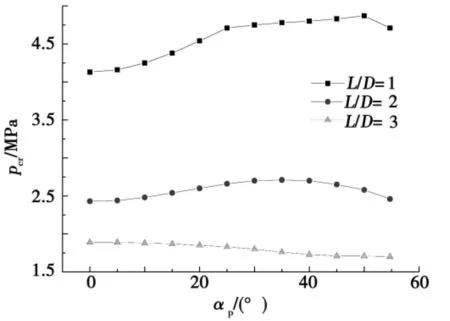
圖4 不同長徑比圓柱殼失穩載荷隨纏繞角變化曲線

2.2 任一長徑比下的最優纏繞角

對于長徑比0.5≤η≤3的復合材料夾層圓柱殼，采用ABAQUS建立結構穩定性有限元計算模型，求解滿足等強度要求的各纏繞方式所對應的臨界失穩載荷，通過復形調優反復迭代與選擇，得到出最大臨界失穩載荷pcr及最優螺旋纏繞方式，如表3所示。其中，η=0.938時，對應圓柱殼長度L=0.5 m，η=1.867時，對應圓柱殼長度為L=1 m。最后，繪制最優纏繞角度隨長徑比的變化規律αp-η曲線及最大臨界失穩載荷隨長徑比的變化規律pcr-η曲線，見圖5、圖6。

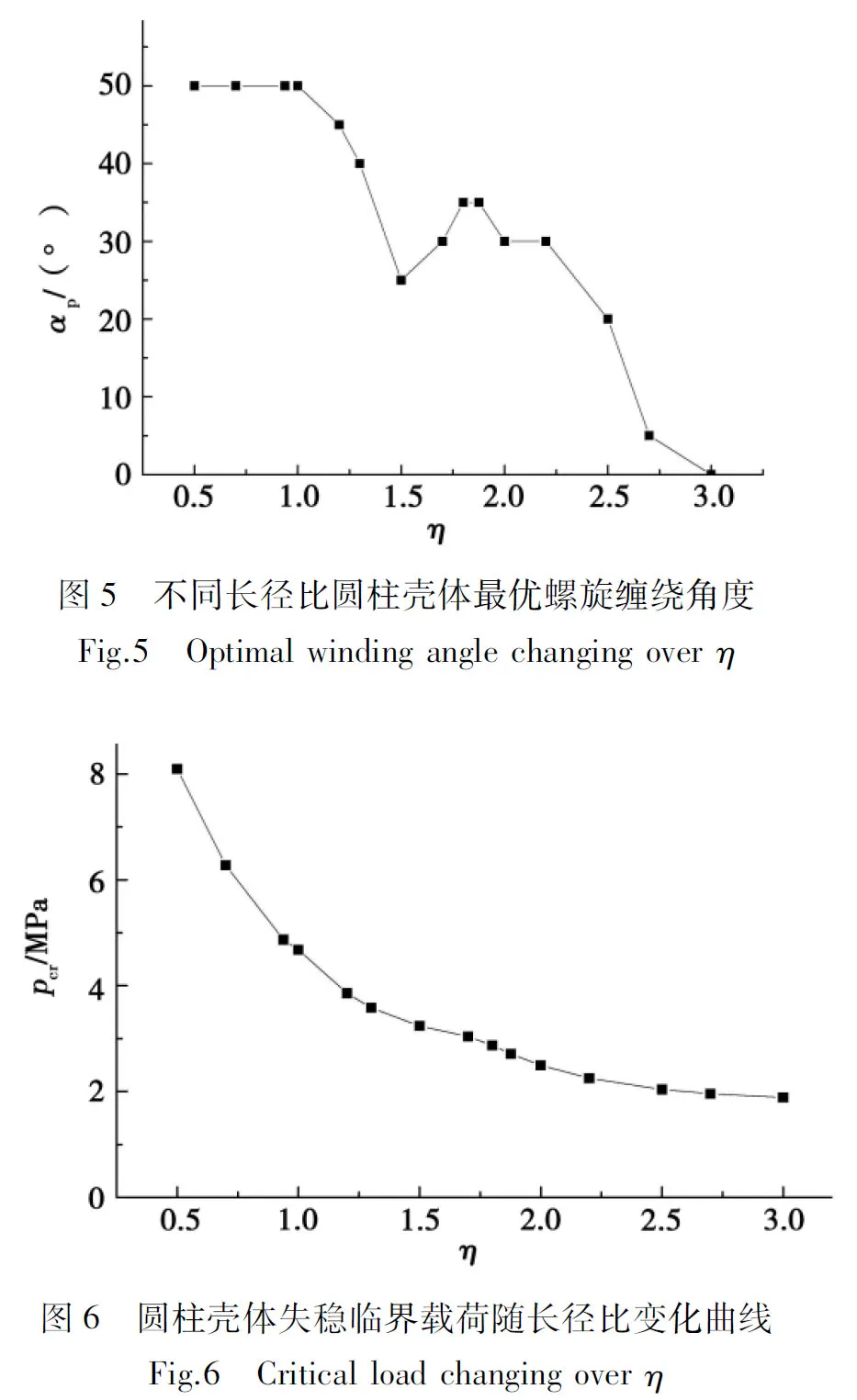
由圖5知，當0.5≤η≤3時，隨長徑比η增加，圓柱殼表層最優螺旋纏繞角從50°逐漸變化至0°，最優纏繞方式從單一螺旋加環型纏繞(0°≤αp≤54.7°)過渡至縱向鋪放加環向纏繞(αp=0°)。由圖6知，最大臨界失穩載荷pcr隨長徑比η的增加而減小，近似呈二次遞減關系，這與經典歐拉屈曲理論一致[9]。

3 結論

通過對夾層復合材料圓柱殼的纏繞表層進行優化設計，得到以下結論。

(1)基于網絡理論，以平衡型穩定纏繞為約束，采用結構等強度設計法，得到表層的最優纏繞方式為螺旋加環型纏繞，纏繞角應滿足α≤54.7°；

(2)對于η=1圓柱殼，隨纏繞角度增加，最大臨界屈曲載荷增加，最優纏繞方式應接近于單一螺旋纏繞，αp≤54.7°；對于η=3圓柱殼，隨纏繞角度增加，最大臨界失穩載荷呈下降趨勢，最優纏繞方式應接近于縱向鋪放加環向纏繞，但此纏繞方式為工藝帶來難度，故當長徑比較大時，需考慮增加艙壁或肋骨；

(3)當0.5≤η≤3時，隨長徑比η增加，最優纏繞方式從單一螺旋加環型纏繞(0°≤αp≤54.7°)過渡至縱向鋪放加環向纏繞(αp=0)，而最大臨界失穩載荷pcr近似呈二次遞減關系。

[1] 陳汝訓．纖維纏繞殼體設計的網絡分析方法[J].固體火箭技術，2003，26(1)：30-32.

[2] 譚三五．基于網格理論的纖維纏繞殼體結構可靠性數字仿真[J]．固體火箭技術，1996，19(1)：12-17．

[3] 胡寬，宋筆鋒，常新龍，等．基于網絡理論的固體火箭發動機纖維纏繞殼體優化設計[J]．兵工學報，2008，29(9)：1099-1103．

[4] 欒宇，丁文輝，林天軍，等．基于蟻群算法的復合材料纏繞殼體鋪層順序優化[J]．計算力學學報，2011，28(2)：248-254．

[5] 祖磊，何欽象，李輔安．纖維纏繞復合材料圓環殼線型設計與優化[J]．宇航材料工藝，2006，36(3)：14-18.

[6] KIM CHEOL-UNG,KANG JI-HO,HONG CHANG-SUN,et al．Optimal design of filament wound structures under internalpressure based on the semi-geodesic path algorithm[J]．Composite Structures，2005 (67)：443-452.

[7] 鄧忠民．飛行器復合材料結構設計基礎[M]．北京：北京航空航天大學出版社，2014．

[8] 陳汝訓．固體火箭發動機設計與研(下)[M]．北京：宇航出版社，1992．

[9] 吳梵，朱錫，梅志遠．船舶結構力學[M]．北京：國防工業出版社，2010．

Surface Layer Optimization of Filament-Wound Sandwich Composite Cylinder

CHEN Yue1LI Huadong2ZHU Xi2ZHU Zixu2

(1 Service College，Naval University of Engineering，Tianjin 300450) (2 Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430003)

Composite，Filament-wound，Sandwich cylinder，Optimal

2016-07-18；

2016-12-30

國家部委基金資助項目(9140A14080914JB11044)；海軍工程大學自然科學基金

陳悅，1989年出生，博士研究生，主要從事船用復合材料及其應用研究。E-mail:chenyue322@126.com

李華東，1984年出生，講師，主要從事復合材料結構設計與應用研究，E-mail:lhd0727@163.com

TB332.1

10.12044/j.issn.1007-2330.2017.03.006