基于多斜率碼鏈的陣列糾刪碼

唐 聃,楊昊澎,王福超

成都信息工程大學 軟件工程學院,成都 610225)(*通信作者電子郵箱tangdan@foxmail.com)

基于多斜率碼鏈的陣列糾刪碼

唐 聃*,楊昊澎,王福超

成都信息工程大學 軟件工程學院,成都 610225)(*通信作者電子郵箱tangdan@foxmail.com)

針對當前大多陣列糾刪碼容錯能力偏低以及構造時需要滿足的約束條件較強的問題,提出一類基于碼鏈構造的陣列糾刪碼。該陣列糾刪碼使用不同斜率碼鏈組織數據元素和校驗元素間的關系,從而能達到理論上不受限制的容錯能力；而在構造時避開了類似素數約束的強約束條件,易于實用和擴展。仿真實驗結果表明,相對于RS(Reed-Solomon)碼,基于多斜率碼鏈陣列糾刪碼在運算效率上的提升超過了2個數量級；在固定的容錯能力下,存儲效率能隨著條塊尺寸的增加而提高。此外,該類陣列碼的修復代價和更新代價為一個固定常量,不會隨著系統規模的擴大或容錯能力的提高而增加。

陣列糾刪碼;容錯;碼鏈;條塊尺寸

0 引言

當前,我們已經跨入到了大數據的時代,各個行業領域產生的數據正爆炸式地持續增長,與之伴隨的是越來越多的數據成為了社會正常運行不可或缺的部分。為應對由數據量的快速增長而帶來的數據存儲可靠性問題,不斷提高單個存儲節點的穩定性當然是一種理論可行的方法；但更加有效的做法是使用多個存儲節點共同構建一個存儲系統,這樣做除了能充分利用既有設備、增加存儲容量、提高數據并行訪問效率外,結合一定的容錯策略后還能有效增強存儲系統的整體可靠性。在這種情況下,通常使用存儲節點的數量來表示存儲系統的規模。目前節點數目超過100的大規模存儲系統已經日益普遍,而谷歌等公司甚至已經擁有了多個節點數目超過3 000的PB級存儲系統[1]。與過去相比,盡管當前單個存儲節點的可靠性已經很高,但是在擁有眾多節點的大規模存儲系統中,一個時間段內多個節點失效的概率依然很高。據卡內基梅隆大學的統計數據顯示,節點數超過300的大規模存儲系統中存儲節點每年的失效替換率約為5.1%[2]。當然,這還是存儲系統在正常使用狀況下的節點失效概率,如果再將洪水、泥石流、地震等自然災害和黑客攻擊等人為因素考慮在內的話,存儲系統的容錯及可靠性增強就更是一個值得關注的問題。

副本技術是目前在存儲系統可靠性增強領域中最為成熟的容錯技術。采用副本技術的容錯方案將多個相同的數據副本存儲到系統的不同節點上,由于每個節點的副本完全相同,通常可不嚴格區分校驗數據(冗余數據)和原始數據,當有節點失效時,由任意一個未失效節點中的副本都能恢復出丟失數據。使用副本技術的容錯方法簡單直觀、易于實現及動態擴展,但是存儲效率過低卻是其巨大的缺陷。假設使用副本技術構造一個t容錯的存儲系統,則需要將原始數據復制成t+1份副本分別存放到不同的節點上,即存儲效率僅為1/(t+1)。顯然,這種極低的存儲空間有效利用率是大規模存儲系統難以接受的。因為存儲系統作為一個整體,不能僅僅考慮某一項性能參數,而應根據應用環境兼顧大多重要性能指標。糾刪碼可以在一定程度上平衡存儲系統中的多種主要性能,是一種日益受到重視的存儲系統容錯方法。目前,用于存儲系統容錯的糾刪碼主要包括了RS類糾刪碼(Reed-SolomonErasureCodes)、LDPC(Low-DensityParity-CheckCodes)類糾刪碼，以及陣列糾刪碼。RS類糾刪碼是目前唯一一類容錯能力不受限制且具備MDS(MaximumDistanceSeparable)性質的糾刪碼,但其編譯碼等運算均在多元有限域上進行,計算復雜度非常高,特別是多元域上的乘法和求逆。因此,以RS類糾刪碼為核心構建存儲系統的容錯方法需要解決的主要問題不是優化編碼,而是如何大幅提高有限域的計算效率。當然,目前也有一些研究者針對這一問題進行了卓有成效的工作,其中最具代表性的工作為Plank等[3]提出的RS碼有限域降階運算方案,以及有限域運算庫GF-Complete[4]。盡管如此,目前RS碼的運算效率仍然很難滿足存儲系統整體運行性能的需要,特別是大規模存儲系統。LDPC碼是源于通信領域的一類糾刪碼,其編碼和譯碼過程完全基于異或運算,與RS碼相比,其糾刪能力不受限且運算效率還要高出幾個數量級。但是,LDPC碼的碼字結構不規則和成功譯碼的概率性卻增加了根據應用環境需求設計出與之適應編碼的難度。目前基于LDPC碼的容錯方法在實際存儲系統中的應用很少,已有方法多是以理論研究或實驗為主[5]。

陣列糾刪碼(通常簡稱為陣列碼)是編譯碼運算均使用二元域上異或運算的一類糾刪碼,運算效率很高,具有的二維編碼結構可完全對應當前多節點存儲系統的數據布局結構,因此很適合在存儲系統中使用。但陣列碼在商用存儲系統中的使用卻非常少,究其原因可以歸納為如下。一是當前陣列碼容錯能力普遍偏低,具備MDS性質的陣列碼的最大容錯能力通常為2和3[6-9];即使是非MDS的陣列碼,在付出了不少的其他性能代價后,最大容錯能力也大多沒有超過20[10-13]。此外,當前大多陣列碼在構造時還對存儲陣列尺寸有較強的限制條件,最典型的是素數限制,即要求存儲系統的條帶或條帶尺寸為一個素數或者和素數嚴格地保持某種線性關系,EVENODD碼[6]、X碼[7]、Star碼[8]和擴展X碼[9]等陣列碼在構造時都存在素數限制。其他一些陣列碼在構造時的沒有這么強的限制條件[10-11],但卻付出了很大的其他性能代價而降低了實用性。比如容錯能力達12以上的Weaver碼[10],該碼在構造時就無需滿足素數限制,但其存儲效率始終低于50%,且還會隨著容錯能力的提升而迅速下降。文獻[14]提出的陣列碼構造方法可以構造出容錯能力在理論上沒有限制的陣列碼,構造時也無需滿足很強的限制條件,但具體構造步驟卻沒有明確指出。

針對陣列碼存在的這些問題,本文提出了一類新的陣列糾刪碼,該碼基于不同斜率的碼鏈構造,能根據應用環境需求預先設置容錯數量,且容錯能力在理論上不受限制。雖然不具備MDS性質,但該陣列碼的存儲效率能在不影響容錯能力等重要性能的前提下,隨著條塊尺寸的增加而不斷提高。此外,該碼在構造時也無需滿足素數限制這樣的強約束條件,已基本具備在存儲系統中使用的條件。

1 基本概念和定義

在存儲編碼領域的常用基本概念,如數據、校驗、冗余、元素、條帶、條塊、水平陣列碼、垂直陣列碼、編碼、譯碼、數據重構等,本文將繼續沿用這些概念的定義而不再贅述[10-13]。下面給出的一些符號和概念的定義則是為了配合說明本文方法而提出的。

碼鏈 陣列碼是一類線性碼,因此在陣列碼中,任意一個校驗元素均由t個數據元素的異或相加得到,換句話說,一個校驗元素與生成它的所有數據元素的異或和為0。而上述元素像一個鏈條一樣分布于存儲陣列中,為敘述方便而簡稱為碼鏈,也可稱為編碼鏈或校驗鏈。而部署碼鏈則是將碼鏈上所有的數據元素進行異或求和,得到對應校驗元素并存儲于相應位置的過程。

斜率 將存儲系統的數據陣列部分(假設尺寸為m×n,其中m和n均為大于1 的正整數)看作一個二維坐標系,以向右的水平軸作為坐標系的正向X軸,以向下的垂直軸作為坐標系的正向Y軸,則所有數據陣列中的元素成為了該坐標系上擁有固定坐標的一個點,假設一條碼鏈上所有存在于數據陣列部分的元素坐標為(x1,y1),(x2,y2),…,(xt,yt),若這些元素的坐標滿足條件(1)則稱該碼鏈存在斜率,且將斜率定義為s=((y2-y1)%n)/(x2-x1)。

(y2-y1)%n=(y3-y2)%n=…=(yt-yt-1)%n

(1)

圖1展示了如何部署一條斜率為1的碼鏈。其中,所有背景色相同的元素異或和為0,共同構成一條完整碼鏈。

圖1 斜率為1的碼鏈

El(i,j):該符號用于標識存儲陣列中第i行第j列的元素,當有多個元素需要表示時,可以使用符號“:”表示出一個范圍區間,如El(i,2:5)表示存儲陣列第i行上的第2到5個元素集合,El(:,j)則用于表示陣列中第j列的所有元素。

2 基于多斜率碼鏈的陣列碼

垂直陣列碼的數據布局結構中,同一條塊中既存儲有數據元素又存儲有冗余元素,具有很好的負載平衡性,但節點間數據的相互依賴性很強,不便于擴展,因此本文的新方法采用了典型的水平陣列布局。關于陣列碼的構造方法有很多,常見的包括圖論構造法、RS糾刪碼映射法、代數模型構造方法和幾何構造法等。這幾種陣列糾刪碼的構造方法各有優點,其中使用幾何形式的構造方法具有最高的計算效率且更加易于計算機軟硬件實現。而本文采用的基于不同斜率碼鏈來組織數據元素和校驗元素間關系的方法就是最典型的一種幾何構造法。

2.1 編碼及數據重構方法

如前所述,為了減少數據及冗余元素間的相互依賴性,文章采用了典型的水平式陣列結構布局。假設存儲系統節點的容錯數量為f,陣列的行數為m,數據陣列部分的列數為n,冗余陣列部分的列數為r,顯然f、m、r為正整數,且m≥2。整個存儲陣列的尺寸為m×(n+r)。若無特別說明,下文在敘述過程中的符號f、m、n、r具有和本段描述相同的含義。

在構造一個f容錯的水平陣列碼時,可在數據陣列部分部署斜率從1開始,并從正負雙向漸進擴大的碼鏈f條,顯然所有碼鏈部署完成后將產生冗余元素f·n個,然后將這些冗余元素按照列優先原則順序放置于各校驗節點上。使用符號d(i,j)來表示數據陣列部分中第i行第j列所對應的元素,而直接使用c(t)表示校驗陣列部分的第t個元素,則存儲陣列各元素的標識如圖2所示。其中：i、j、t為正整數,且1≤i≤m,1≤j≤n,1≤t≤f·n。

圖2 存儲陣列的元素標識

在上述數據元素和冗余元素的標識體系下,任意一個校驗元素均可使用式(2)計算得出：

(2)

其中：運算符“「?”表示向上取整；“%”表示取模;lr表示產生當前校驗元素使用的是第lr條碼鏈；lc則表示該條碼鏈是第lc次被使用。lr和lc的計算公式如下：

lr=[(t-1)/n]+1

(3)

lc=(t-1)%n+1

(4)

例1 對一個最大容錯能力為3,且條塊尺寸為3的存儲陣列部署碼鏈,其中該存儲陣列的數據陣列部分有7列。

如前所述,最大容錯能力f為3,數據陣列部分的尺寸為3×7,則校驗元素的數目為21個,因此校驗陣列部分的列數也為7。最大容錯能力為3,因此需要部署斜率為1、-1、2的碼鏈各一條,具體部署過程如圖3所示,其中背景色相同的元素異或和為0。

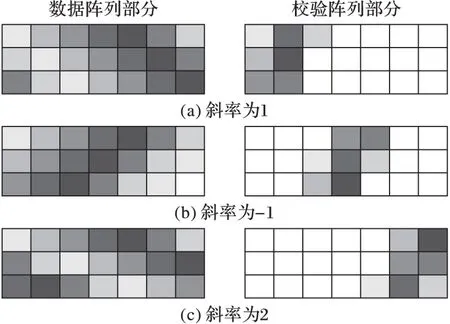
圖3 斜率為1、-1、2的碼鏈部署

用本文方法可以很容易地根據應用環境需求構造出任意容錯能力的陣列碼。而接下來將簡要介紹當有節點失效后如何進行恢復重構。需要說明的是,本文僅考慮節點錯誤的情況,即整個存儲節點失效而導致該節點上所有數據元素的丟失,這也對應存儲陣列中整列的數據失效。失效節點上數據恢復的基本思想可以歸結為一句話,即尋找只存在唯一一個失效元素的碼鏈,顯然該碼鏈上的失效元素可由其他有效元素計算恢復。不斷重復這一過程,直到所有失效元素被恢復。

例2 假設在例1所示的存儲系統中節點1、3、5失效,即在將失效節點替換更新后,存儲陣列中數據陣列部分的1、3、5列上的元素數值變得未知,整個數據恢復過程如圖4所示。其中有“X”標識的元素表示數值未知的失效元素,而具有相同背景色的元素為僅有一個失效元素的碼鏈,將該碼鏈上其他元素進行異或相加可恢復失效元素。

圖4 失效數據的成功恢復過程

繼續擴展例2,假設數據陣列部分的尺寸為,仍然是1、3、5列上的元素失效。然而,如圖5所示,此時卻無法找出任何一條僅包含一個失效元素的碼鏈。在此情況下,該存儲系統中所有的數據丟失。

1.2.1 觀察組和對照組在院期間均進行常規的術后自我護理知識宣教、免費發放宣教資料等進行造口護理指導。

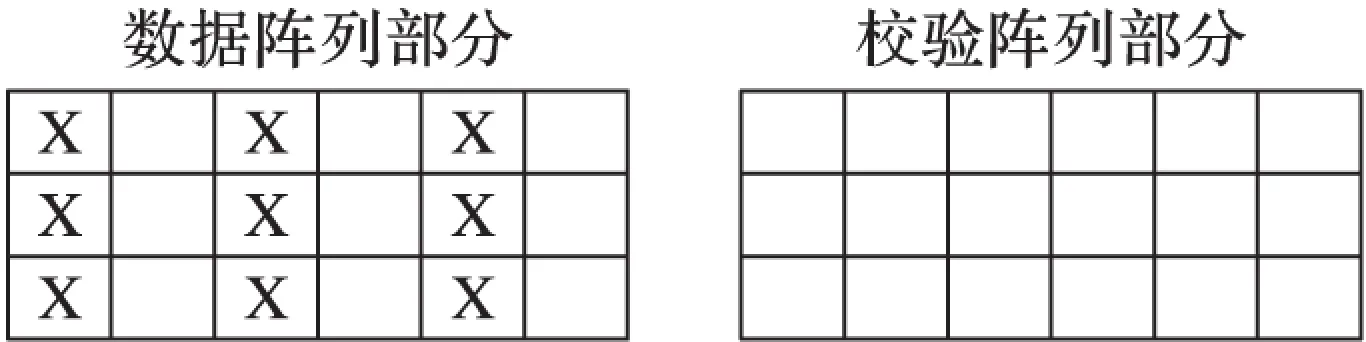
圖5 失敗的數據恢復

2.2 約束條件及容錯能力保證

從例2可以得出如下結論,如果需要使得條塊尺寸為3的存儲陣列容錯能力達到3,除了需要部署3條斜率不同的碼鏈外,數據陣列部分的列數至少不能小于7,否則將無法保證容錯能力。將這一結論進一步擴展,即僅僅使用不同斜率的f條碼鏈來構造陣列碼不能保證容錯能力一定是f,容錯數量和陣列尺寸還需要滿足某種條件。在此,首先給出容錯能力f、條塊尺寸m和數據陣列部分列數n應滿足的條件:n≥m·f-f+1。下面將證明在滿足該約束條件的情況下,容錯能力就可以得到保證。

對于水平布局的陣列碼,節點級錯誤的發生情況可以分為如下三種:一是全部失效節點在校驗陣列部分,二是校驗陣列部分和數據陣列部分均有失效節點,三是失效節點全部在數據陣列部分。當所有失效節點都發生于校驗陣列部分時,僅僅需要在替換失效節點后重新做一次編碼操作即可,這是數據重構最簡單的情況。當數據陣列部分和校驗陣列部分都有失效節點出現時,也相對容易處理。在f容錯的陣列碼中,每個數據元素均有f條碼鏈通過,因此一個數據元素與f個校驗元素相關。根據約束條件可知,n>m,所以兩個與同一數據元素相關的校驗元素一定不會出現在同一列。由此,所有數據陣列部分的失效元素可以被全部恢復,之后再根據編碼方法就可以將校驗陣列部分的全部失效元素恢復。而對于f個失效節點全部存在于數據陣列部分的情況,下面將采用數學歸納法進行證明。

首先,不妨將數據陣列部分f個失效列記作E1,E2,…,Ef,其中di記為錯誤列Ei與其右鄰失效列之間的距離, 不妨假設max(d1,d2,…,df)=df,其中i=1,2,…,f。因此,由鴿籠原理可知,df≥m成立。當f=1時,即僅有一個失效列時,將該列記作E1。由碼鏈部署方法可知,每一個數據元素均有一條碼鏈通過,顯然該列上的所有失效元素可以成功恢復。假設當f=k時所有失效元素可以被成功恢復,其中k為正整數。下面討論f=k+1的情況。由前提條件可知,max(d1,d2,…,dk)=dk≥m。因此,若不等式d1≥「m/2?成立,則顯然第一個失效列E1上的所有元素均可由斜率為1或-1的碼鏈恢復。同理,若dk≥「m/2?成立,則最后一個失效列Ek+1上的所有元素均可由斜率為1或-1的碼鏈恢復。至此,上述兩種情況均可化為f=k的情況,而根據前述假設可知,所有失效數據能得到恢復。而當d1<「m/2?且dk<「m/2?時,顯然所有失效列上的第一個失效元素可以被斜率為±1,±2,…,±k,k+1的碼鏈恢復。而所有失效列上第一行的失效元素被成功恢復后,只需不斷重復上述相同的步驟,剩余失效元素可被有效恢復。

因此,不等式n≥m·f-f+1即是構造陣列碼時需要滿足的約束條件,不難看出,與前文所述的素數約束相比,本文方法的約束條件非常容易滿足,也有根據實用環境需求動態擴展的空間,與大多已有陣列碼相比,本文方法的限制條件強度已經有了很大幅度的降低。

3 實驗與分析

3.1 運算工作量

由于大多陣列碼的碼字結構不規則而很難用一個確切的公式來表達編碼或數據重構的總體工作量,因此,通常使用生成單個校驗位所需要經過異或運算的次數來衡量其編碼的復雜度,采用恢復單個丟失數據位需要經過的異或運算的次數來衡量其數據恢復的復雜度。由前文可知,每條碼鏈的長度均為m+1,所以生成單個校驗位或者恢復單個失效元素所需的計算工作量均為m-1。然而,條帶尺寸會隨著條塊尺寸m或容錯能力f的擴大而增加,這就意味著校驗位的數量也將增加,即總體運算量加大。因此,存儲陣列的條塊尺寸以及容錯能力的變化對編碼和數據恢復運算量的影響是需要考慮的一個因素。假設條塊尺寸200,容錯能力為50的情況下,以存儲1 GB的數據為例,生成所有校驗位或恢復50個節點的失效數據所需要的異或運算次數約為4.2×109,這些運算量用一臺主頻為3.2 GHz的普通個人電腦大概也只需要16 s就能完成。圖6顯示了條塊尺寸對陣列碼編碼和數據恢復運算量的影響情況,而圖7則顯示了容錯能力對編碼和數據恢復運算量的影響情況。

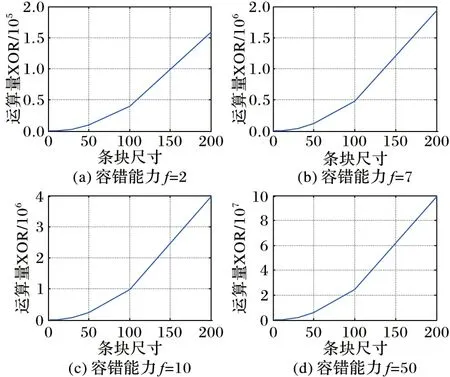
圖6 條塊尺寸對運算量的影響

圖7 容錯能力對運算量的影響

如前所述,以存儲效率為標準,目前的陣列碼可以劃分為MDS編碼和非MDS編碼。MDS編碼在存儲效率上具有理論上的最優值,其典型代表包括以EVENODD碼[6]、X碼[7]、Star碼[8]和擴展X碼[9]等。但是具有MDS性質的陣列碼通常的容錯能力僅為2或3, 這顯然不能滿足現代大規模存儲系統的可靠性增強需求。而為了提高陣列碼的容錯能力, 研究者們則設計出一些不具備MDS性質的陣列碼,其容錯能力與具有MDS性質的陣列碼相比有較大提升(通常在10個以上),即通過降低存儲效率(在不小于復制冗余策略的前提下)以換取更高的容錯能力,這類編碼的典型代表包括Weaver碼[10]、Hover碼[11]和Grid碼[12]等。但大多對于存儲效率的犧牲很大,比如Weaver碼在容錯能力為10時,其存儲效率還不足20%。而本文提出的編碼也是一種典型的非MDS陣列編碼,因此也不具有最優的存儲效率,但可以在保證較高容錯能力的前提下,達到較高的存儲效率。如圖8所示,在具有較高容錯能力時,本文提出的陣列碼依然可以達到較高的存儲效率。

圖8 存儲效率的變化

3.3 修復代價和更新代價

修復代價通常是指重構一個失效的數據元素所需要涉及到讀操作的存儲節點總數。修復代價是存儲系統中一個重要的性能指標,與數據重構、數據更新、降低讀寫等均有密切的關系。由前述碼鏈的部署方法可得,每條碼鏈上均有m+1(m個數據元素和1個校驗元素)個元素,因此,重構一個失效數據元素需要涉及的節點數總是m,且不會隨著存儲系統規模和容錯能力的增加而增大。

更新代價是水平布局陣列碼中的一個特有指標,它是指一個最小的數據位改變時所需要涉及到的校驗節點數。數據更新比較頻繁時,更新代價過高會導致校驗節點的訪問過熱而降低存儲系統的整體I/O性能。由本文陣列碼構造方法可知,每個數據元素均剛好有f條不同碼鏈通過,即每個數據元素均有f個不同的校驗元素與之相關。換句話說,當任意一個數據元素改變時,總是會涉及到f個校驗節點,即更新代價恒為f,而這也已經達到了f容錯陣列碼更新代價的理論最優值。

4 結語

本文使用不同斜率碼鏈構造出了一類容錯能力理論上不受限制的陣列糾刪碼,其結構簡潔,有利于計算機軟硬件實現。該碼涉及的所有計算均使用二進制的異或運算,具有極高的運算效率;而構造時也無需滿足素數約束等強約束條件,易于實用且便于擴展。雖然該碼不具備MDS性質,但存儲效率可以通過條塊尺寸的增加而不斷提高。此外,該碼的修復代價和更新代價均為一個常量,不會隨著系統規模或容錯能力的提高而增加。

)

[1]SATHIAMOORTHYM,ASTERISM,PAPAILIOPOULOSD,etal.XORingelephants:novelerasurecodesforbigdata[J].ProceedingsoftheVLDBEndowment, 2013, 6(5): 325-336.

[2]SCHROEDERB,GIBSONGA.Diskfailuresintherealworld:whatdoesanMTTFof1 000 000hoursmeantoyou?[C]//FAST2007:Proceedingsofthe5thUSENIXConferenceonFileandStorageTechnologies.Berkeley,CA:USENIXAssociation, 2007:1-16.

[3]PLANKJS,XUL.OptimizingCauchyReed-Solomoncodesforfault-tolerantnetworkstorageapplications[C]//NCA2006:ProceedingsoftheFifthIEEEInternationalSymposiumonNetworkComputingandApplications.Washington,DC:IEEEComputerSociety, 2006:173-180.

[4]PLANKJS,GREENANKM,MILLEREL.ScreamingfastGaloisfieldarithmeticusingIntelSIMDinstructions[C]//FAST2013:Proceedingsofthe11thUSENIXConferenceonFileandStorageTechnologies.Berkeley,CA:USENIXAssociation, 2013: 299-306.

[5]JANAKIRAMB,CHANDRAMG,ARAVINDKG,etal.SpreadStore:aLDPCerasurecodeschemefordistributedstoragesystem[C]//Proceedingsofthe2010InternationalConferenceonDataStorageandDataEngineering.Piscataway,NJ:IEEE, 2010: 154-158.

[6]BLAUMM,BRADYJ,BRUCKJ,etal.EVENODD:anefficientschemefortoleratingdoublediskfailuresinRAIDarchitectures[J].IEEETransactionsonComputers, 1995, 44(2): 192-202.

[7]XUL,BRUCKJ.X-code:MDSarraycodeswithoptimalencoding[J].IEEETransactionsonInformationTheory, 1999, 45(1): 272-276.

[8]HUANGC,XUL.STAR:anefficientcodingschemeforcorrectingtriplestoragenodefailures[J].IEEETransactionsonComputers, 2008, 57(7): 889-901.

[9] 孟慶春. 應用于分布式存儲系統上的糾刪碼技術研究[D]. 北京: 中國科學院研究生院, 2007.(MENGQC.Researchoferasurecodesappliedindistributedstoragesystem[D].Beijing:GraduateUniversityoftheChineseAcademyofSciences, 2007.)

[10]HAFNERJL.WEAVERcodes:highlyfaulttoleranterasurecodesforstoragesystems[C]//FAST2005:Proceedingsofthe4thConferenceonUSENIXConferenceonFileandStorageTechnologies.Berkeley,CA:USENIXAssociation, 2005, 4: 211-224.

[11]HAFNERJL.HoVererasurecodesfordiskarrays[C]//DSN2006:Proceedingsofthe2006InternationalConferenceonDependableSystemsandNetworks.Washington,DC:IEEEComputerSociety, 2006: 217-226.

[12]LIM,SHUJ,ZHENGW.GRIDcodes:strip-basederasurecodeswithhighfaulttoleranceforstoragesystems[J].ACMTransactionsonStorage, 2009, 4(4):ArticleNo. 15.

[13] 陳崢. 一類新的陣列糾刪碼理論及應用研究[D]. 北京: 中國科學院研究生院, 2009.(CHENZ.Aclassofarrayerasurecodesandtheirapplications[D].Beijing:GraduateUniversityoftheChineseAcademyofSciences, 2009.)

[14] 唐聃, 舒紅平. 一類多容錯的陣列糾刪碼[J]. 中國科學: 信息科學, 2016, 46(4): 523-538.(TANGD,SHUHP.Aclassofarrayerasurecodeswithhighfault-tolerance[J].ScienceChina:InformationSciences, 2016, 46(4): 523-538.)

ThisworkispartiallysupportedbytheNationalNaturalScienceFoundationofChina(61501064, 61501063),theYouthScienceandTechnologyFundofSichuanProvince(2017JQ0057).

TANG Dan, born in 1982, Ph. D., associate professor. His research interests include big data, cloud computing, coding theory.

Array erasure codes based on coding chains with multiple slopes

TANG Dan*, YANG Haopeng, WANG Fuchao

(College of Software Engineering, Chengdu University of Information Technology, Chengdu Sichuan 610225, China)

In view of the problem that the fault tolerance capability is low and strong constraint conditions need to be satisfied in the construction of most array erasure codes at present, a new type of array erasure codes based on coding chains was proposed. In the new array erasure codes, coding chains with different slopes were used to organize the relationship among data elements and check elements, so as to achieve infinite fault tolerance capability in theory; the strong constraint conditions like the prime number limitation was avoided in construction, which is easy to be practical and extensible. Simulation results show that, compared with Reed-Solomon codes (RS codes), the efficiency of the proposed array erasure codes based on coding chains is more than 2 orders of magnitude; under the condition of fixed fault tolerance, its storage efficiency can be improved with the increase of the strip size. In addition, the update penalty and repair cost of the array codes is a fixed constant, which will not increase with the expansion of the storage system scale or the increase of fault tolerance capability.

array erasure code; fault tolerance; coding chain; strip size

2016- 10- 08;

2016- 11- 25。

國家自然科學基金資助項目(61501064, 61501063);四川省青年科技基金資助項目(2017JQ0057)。

唐聃(1982—),男,四川成都人,副教授,博士,CCF會員,主要研究方向:大數據、云計算、編碼理論。

1001- 9081(2017)04- 0936- 05

10.11772/j.issn.1001- 9081.2017.04.0936

TP302.8

A