側向噴流非定常干擾效應研究*

任淑杰，陳剛，劉永利，張慶兵

(北京電子工程總體研究所，北京 100854)

側向噴流非定常干擾效應研究*

任淑杰，陳剛，劉永利，張慶兵

(北京電子工程總體研究所，北京 100854)

通過多狀態對比分析，給出了適用于此側向噴流問題的非定常數值計算方法，并進行了側向噴流開啟和關閉后非定常流場建立和消退過程的研究。結果表明：噴流啟動后，在1.5 ms時，噴流強度和高度達到最大，但此時激波不穩定，進行不穩定擺動，至5 ms時，噴流干擾流場完全建立并達到穩定狀態。噴流關閉后，噴流前方弓形激波的強度和高度迅速減小，噴流影響區也迅速減小，由于氣流粘性產生的延遲效應，至10 ms時，噴流干擾影響基本消退。

側向噴流；非定常；雙時間步方法；噴流開啟；噴流關閉；壓力分布

0 引言

在高空和低速情況下，來流動壓小，飛行器舵面控制布局受到嚴重的挑戰，舵面控制能力不足；在有特殊快速機動要求時，舵面控制響應慢，無法滿足高機動性能的控制需求。而側向噴流控制技術可直接提供反作用力，用于飛行器的姿態與軌道控制，響應時間短，不受來流動壓的影響。當舵面控制無法滿足控制需求時，側向噴流控制技術可以補充或替代舵面控制[1-3]。

側向噴流干擾流場的建立是一個通過流場參數傳遞和匹配而趨于平衡的動態過程[4]。非定常性是側噴干擾流場的重要特征，主要體現在干擾流場建立和消退過程的非定常特性以及分離流動導致的流場結構的非定常特性，并且對噴流直接力作用效應、飛行器瞬態氣動特性、飛行穩定性等會產生直接的影響[5-6]。然而，工程應用中對側向噴流非定常效應的認識還不夠深入，如何考慮噴流氣動干擾力的非定常效應仍沒有解決。

本文重點關注噴流干擾流場建立和消退過程的非定常特性，采用數值模擬技術對側向噴流非定常干擾效應進行研究，為噴流干擾的機理分析、預測噴流實際控制力和力矩及噴流干擾影響提供支撐，為總體及控制設計提供參考。

1 數值計算參數影響分析

1.1 非定常數值計算方法

本文采用有限體積法求解三維可壓縮雷諾平均Navier-Stokes方程，無粘項采用二階精度TVD格式進行離散并使用Minmod限制器，粘性項采用二階中心差分格式進行離散，時間推進選用點隱式方法。

側向噴流非定常干擾流動的計算，必須使用時間和空間均為二階以上精度的計算方法。本文采用雙時間步方法[7-8]來滿足時間二階精度計算要求。雙時間步方法引入了2個可調整參數，即物理時間步長和內迭代收斂判據。

采用湍流模式理論來模擬湍流現象，是現階段解決側向噴流非定常干擾流動問題的主要手段，本文采用Spalart-Allmaras，k-epsilon，k-omega SST湍流模型，分別研究了3個湍流模型對計算結果的影響。計算模型采用文獻[1]中的錐柱裙外形，噴口位于柱段位置的0°子午線上，噴口噴射方向為垂直柱段周向向外。采用分塊對接網格技術，建立模型高質量的貼體計算網格，噴口處網格采用“O”型網格處理方式，噴口噴射方向網格分布密集，以精確模擬噴流干擾流動。圖1給出了所建立的噴口附近網格分布。

在非定常計算中，來流馬赫數為7，噴管貯室總壓隨時間的變化曲線如圖2所示，貯室總溫為293.15 K，數值模擬噴流開啟與關閉后噴流干擾流場的建立與消退過程。

圖1 噴口附近網格分布Fig.1 Grid distribution of jet nozzle

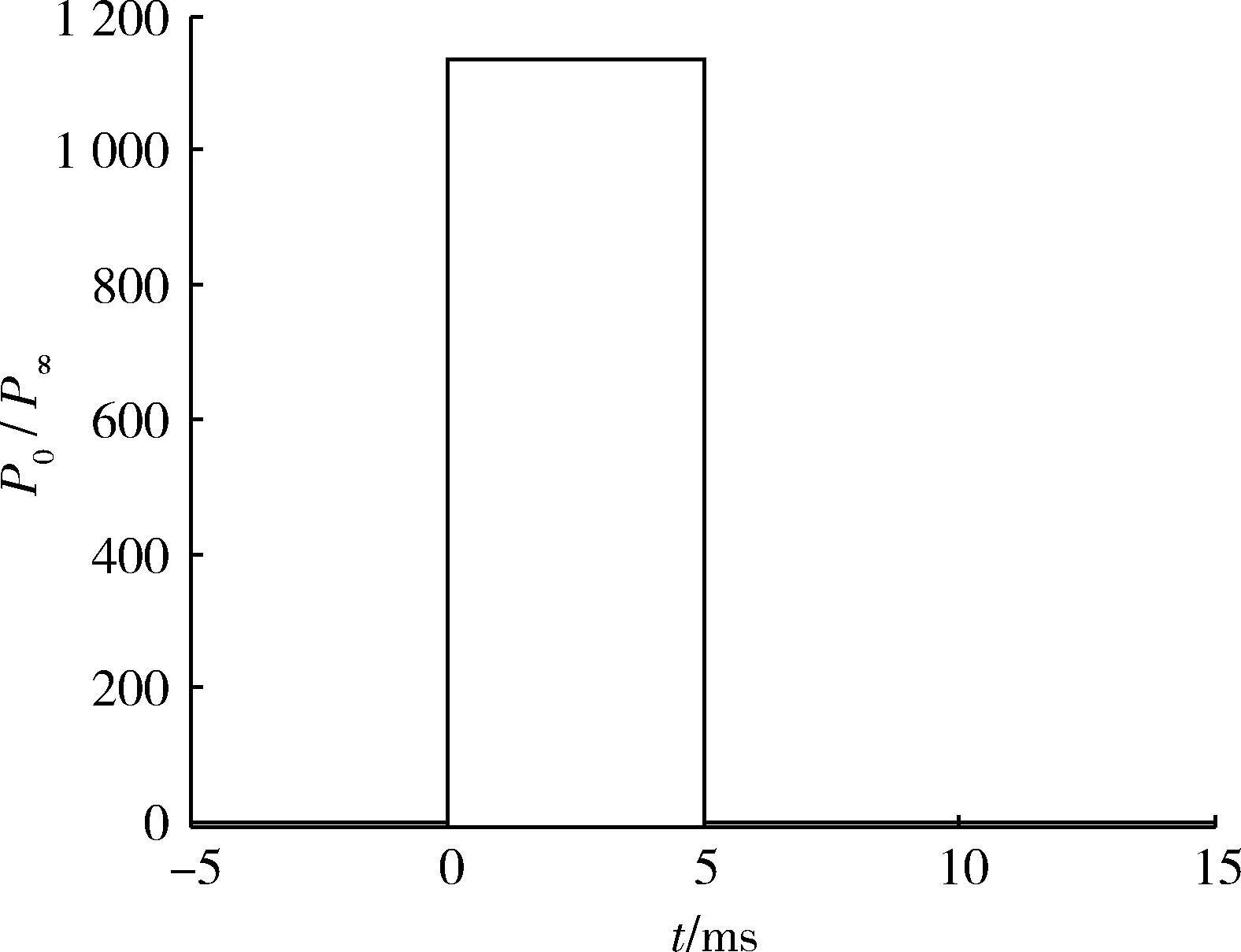
圖2 噴管貯室總壓隨時間變化曲線Fig.2 Curves of total pressure of nozzle chamber with time

1.2 計算參數影響分析

本節選用不同的物理時間步長(Δt為1e-6 s，2e-6 s，5e-6 s)、內迭代收斂判據(Tol分別為0.10，0.05，0.01)、湍流模型(Spalart-Allmaras，k-epsilon，k-omega SST)計算了高超聲速條件下非定常噴流流場建立過程，圖3～5給出了0°子午線壓力分布。可以看出，噴流流場建立的不同時刻，不同物理時間步長對非定常流場的建立過程有一定影響，在噴流流場完全建立后(如圖3b)物理時間步長的影響可以忽略，故后續計算時均選用Δt=1e-6 s；不同內迭代收斂判據的計算結果保持了很高的一致性，從而認為Tol=0.1即可滿足計算要求；不同湍流模型對非定常流場的建立過程有一定影響，在噴流流場完全建立后(如圖5b))湍流模型的影響可以忽略，且SA與k-omega SST的計算結果保持了很高的一致性，故后續計算時均選用SA湍流模型[9]。圖6給出了計算和試驗壓力分布曲線對比，可以看出本文計算方法和計算參數基本可行。

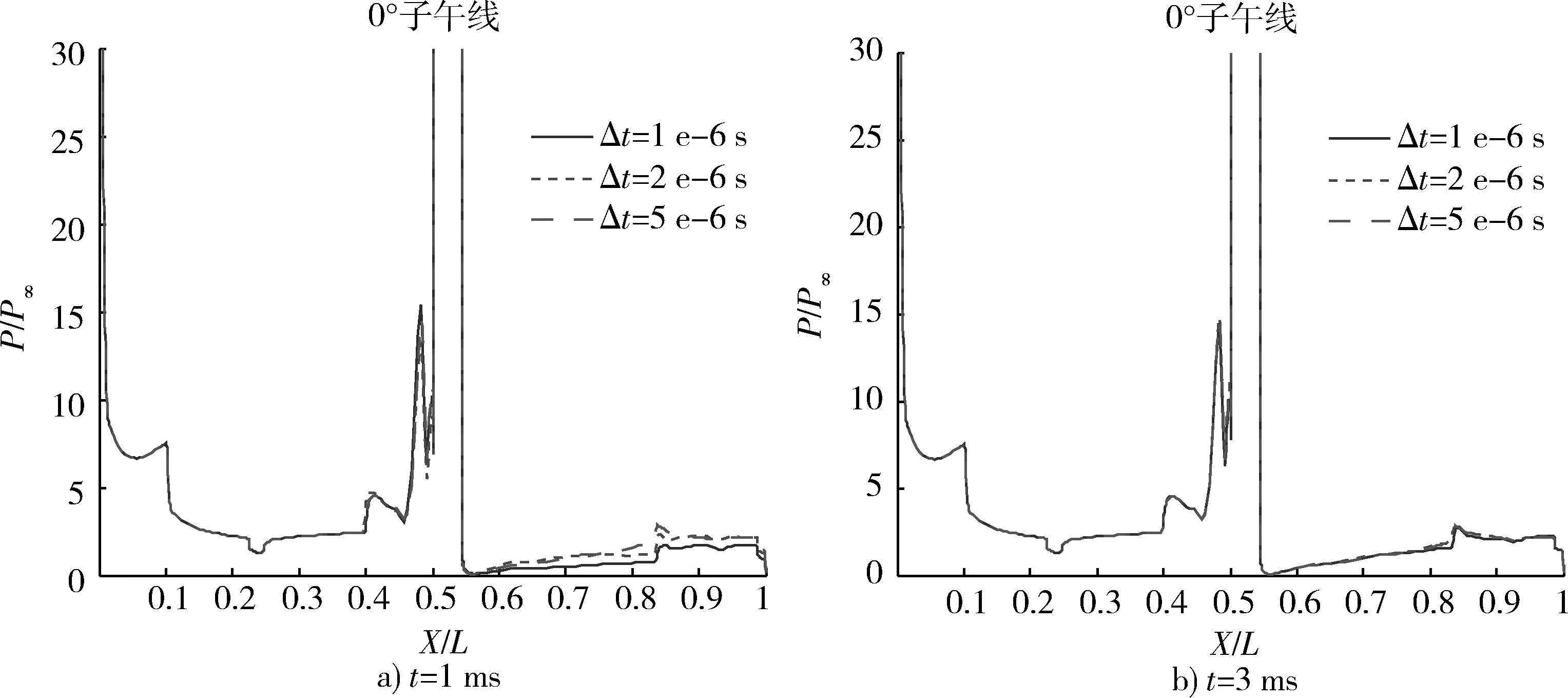
圖3 不同時間步長條件下壓力分布曲線Fig.3 Pressure distribution curve under different time steps

圖4 不同內迭代收斂判據條件下壓力分布曲線Fig.4 Pressure distribution curve under different inner iteration convergence criteria

2 非定常噴流干擾特性

2.1 噴流啟動后干擾流場發展歷程

圖7給出了噴流開啟后不同時刻壁面及對稱面壓力云圖，圖8～9給出了噴流開啟后物面壓力分布曲線。0.1 ms時，噴流作用尚局限在噴口附近，在噴口前方有一道微弱的弓形激波，激波高度比較低；0.3 ms時，噴流前方弓形激波的高度和強度有了明顯的增強，噴流影響區域擴大，噴口前壓力增大，噴口后壓力降低；0.5 ms時，弓形激波的高度和強度繼續加大，分離激波的影響范圍有明顯增加，噴流干擾影響已達到下表面，形成了微弱的包裹效應；1.0 ms時，噴口前壓力達到峰值；1.5 ms時，噴口前影響區域達到最大，之后，隨著時間累積，噴口前影響區域基本不變，噴口前壓力分布也基本不變；1.5 ms時，噴流強度和高度達到最大，但此時激波不穩定；在1.5～3.5 ms這一范圍，弓形激波進行不穩定擺動；隨后噴流流場逐漸趨于穩定，至5 ms時，噴流流場完全穩定[10]。

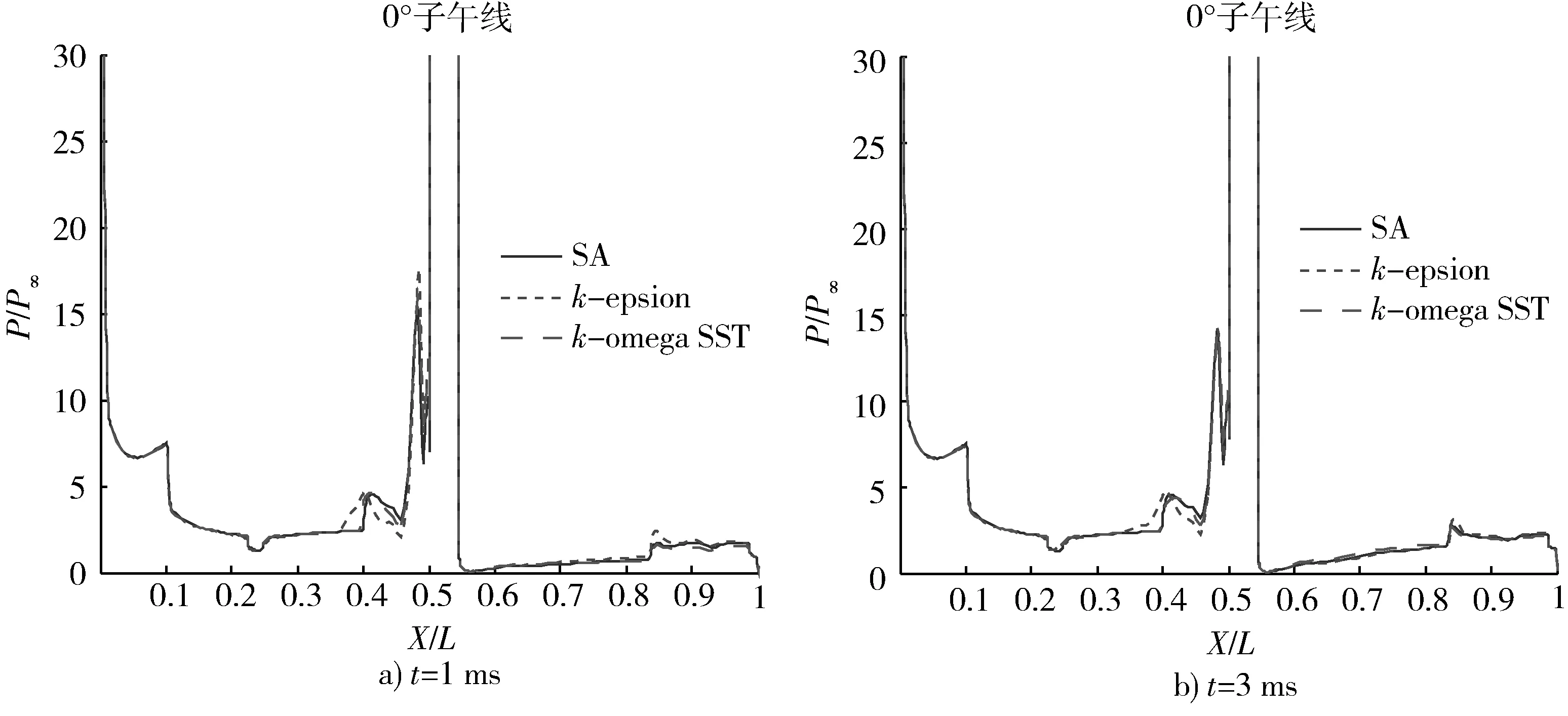
圖5 不同湍流模型條件下壓力分布曲線Fig.5 Pressure distribution curve under different turbulence models

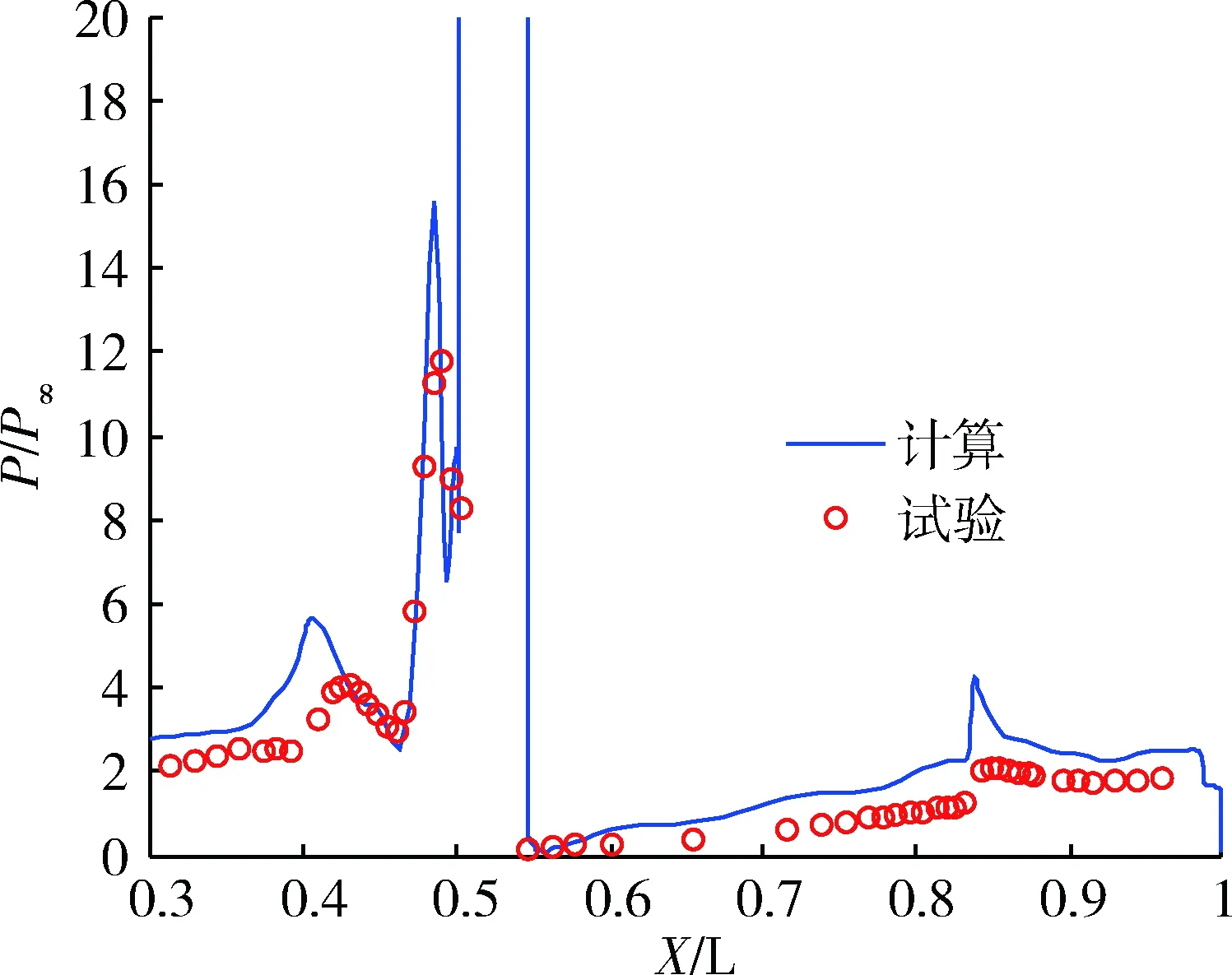
圖6 計算和試驗壓力分布曲線對比Fig.6 Comparison of calculated and experimental pressure distribution curve

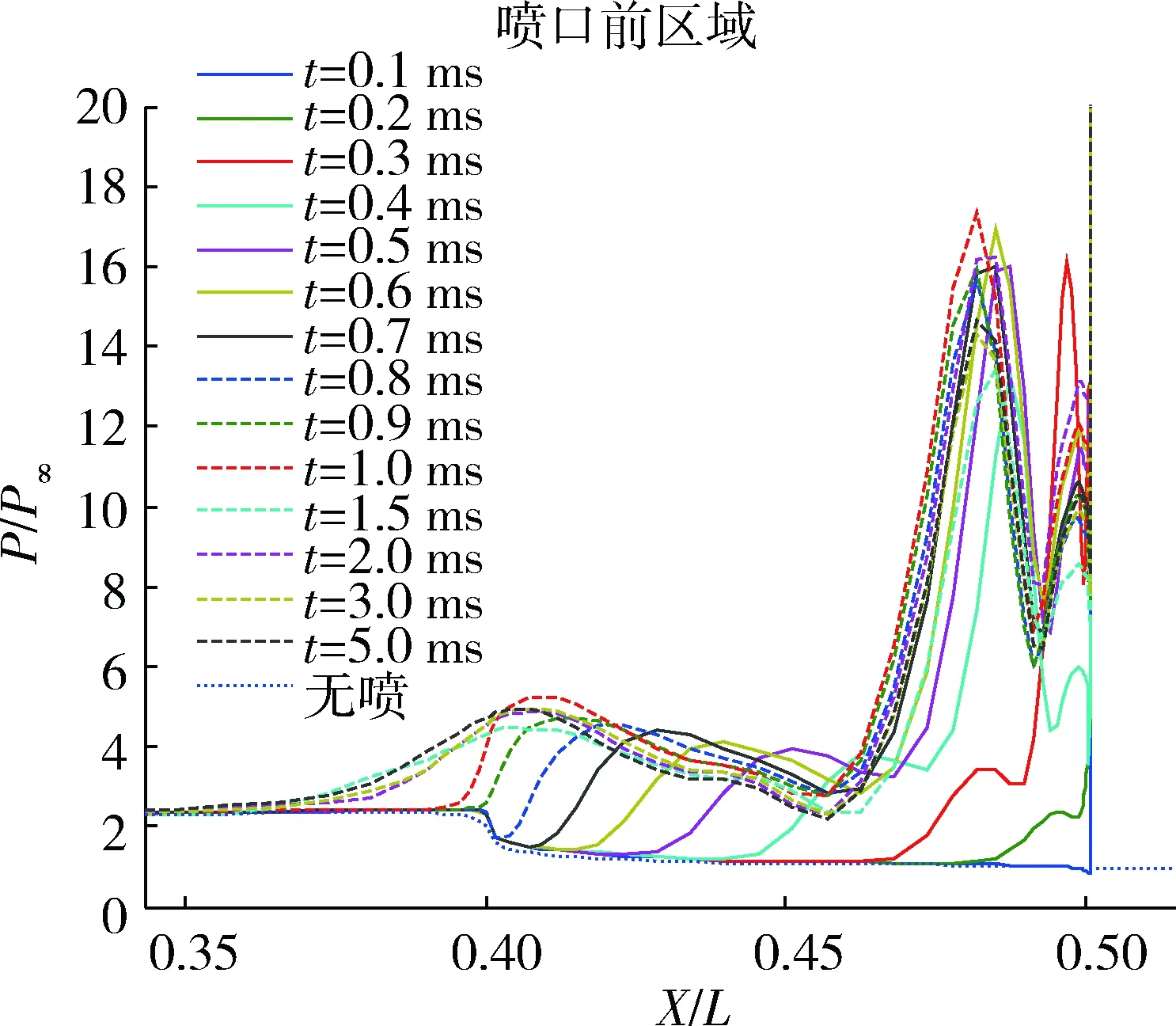
圖8 噴口前區域壓力分布(噴流開啟)Fig.8 Pressure distribution in front of nozzle (jet on)

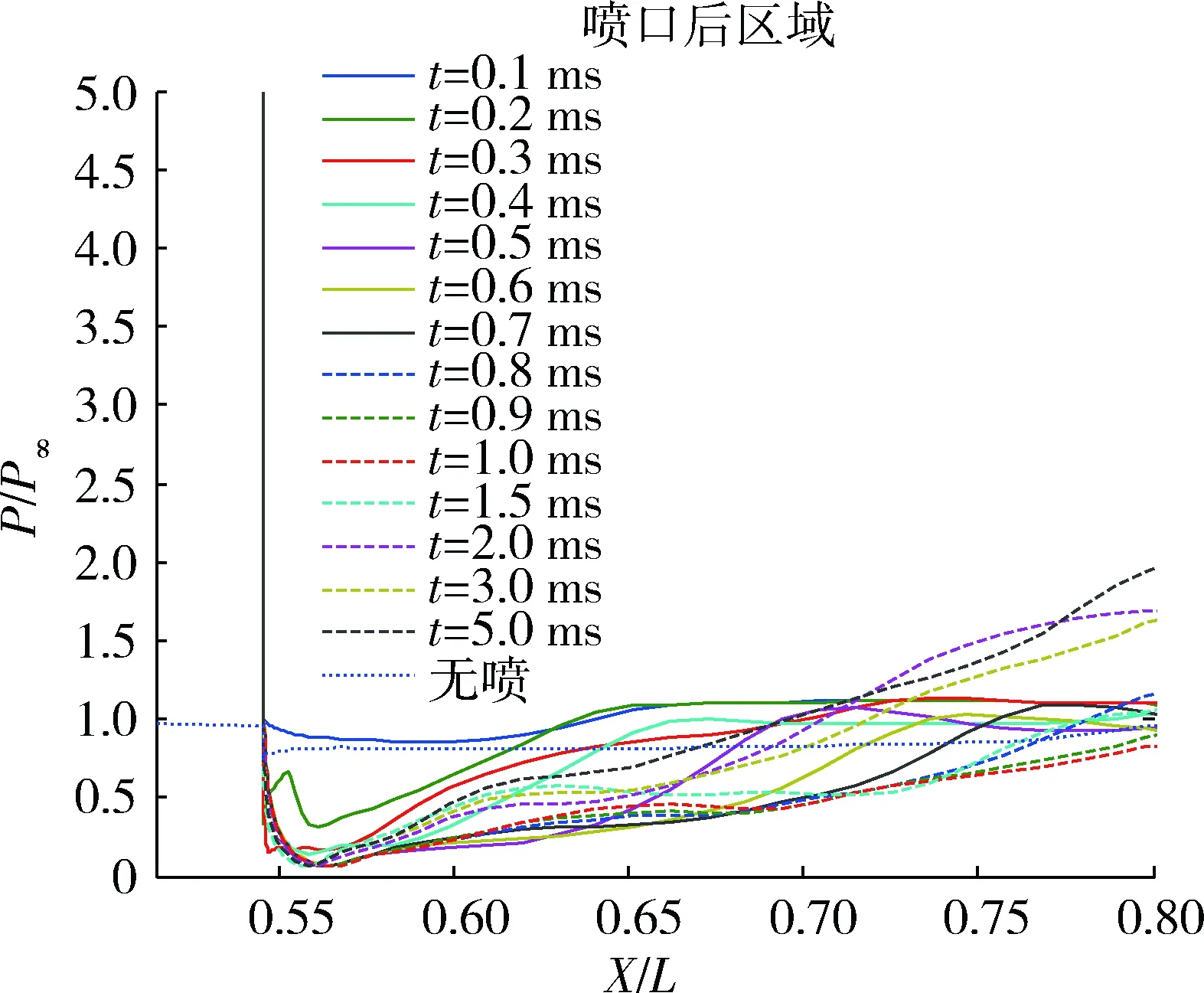
圖9 噴口后區域壓力分布(噴流開啟)Fig.9 Pressure distribution inrear end of nozzle (jet on)

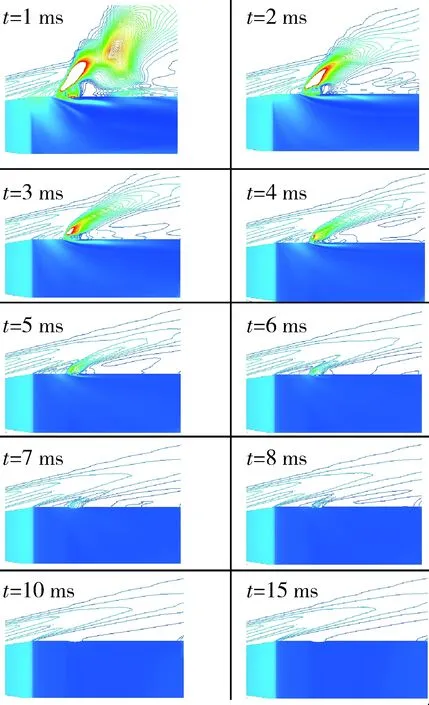
圖10 壁面及對稱面壓力云圖(噴流關閉)Fig.10 Pressure cloud charts of wall and symmetry surface (jet off)

2.2 噴流關閉后干擾流場發展歷程

圖10給出了噴流關閉后不同時刻壁面及對稱面壓力云圖，圖11～12給出了噴流關閉后物面壓力分布曲線。可以看到，噴流關閉后，噴流前方弓形激波的強度和高度迅速減小，噴口前后區域的壓力迅速減小，噴流影響區也迅速減小，至10 ms時，噴流干擾影響消退，噴口前后表面壓力分布特性與無噴時表面壓力分布特性基本一致。由于氣流粘性的影響，造成噴流干擾流場在發動機關閉后較長時間才能恢復到穩態，存在延遲效應[11-15]。

2.3 飛行參數對噴流干擾非定常特性的影響

圖13給出了噴流開啟后不同時刻各個馬赫數條件下0°子午線壓力分布變化情況。可以看出，隨著馬赫數升高，噴口前后區域壓力均有所提高，且噴口前區域取得壓力峰值的位置基本不變，噴口后壓力分布變化規律也基本一致。

圖14給出了噴流開啟后不同時刻各個攻角條件下噴口前區域、噴口后區域壓力分布變化情況。正攻角時，噴口處于背風面。可以看出，隨著攻角增大，噴口前區域壓力均有所降低，且取得壓力峰值的位置向遠離噴口位置的前向移動；隨著攻角增大，噴口后區域壓力也有所降低。

圖15給出了不同馬赫數條件下推力作用點相對質心的相對偏移量隨時間變化曲線。可以看出，不同馬赫數條件下，推力作用點相對質心的相對偏移量隨時間變化規律基本一致。噴流開啟后，在0～1.5 ms或0～2.0 ms時，推力作用點相對質心向前偏移，其中在1～1.2 ms向前偏移量最大，之后推力作用點相對質心向后偏移并逐漸趨于穩定；馬赫數越高，推力作用點相對質心越向后偏移；噴流關閉0～10 ms內，噴流干擾的影響仍然存在，且噴流進行不穩定擺動，造成推力作用點相對質心也進行不規則偏移，之后偏移量逐漸趨于穩定。

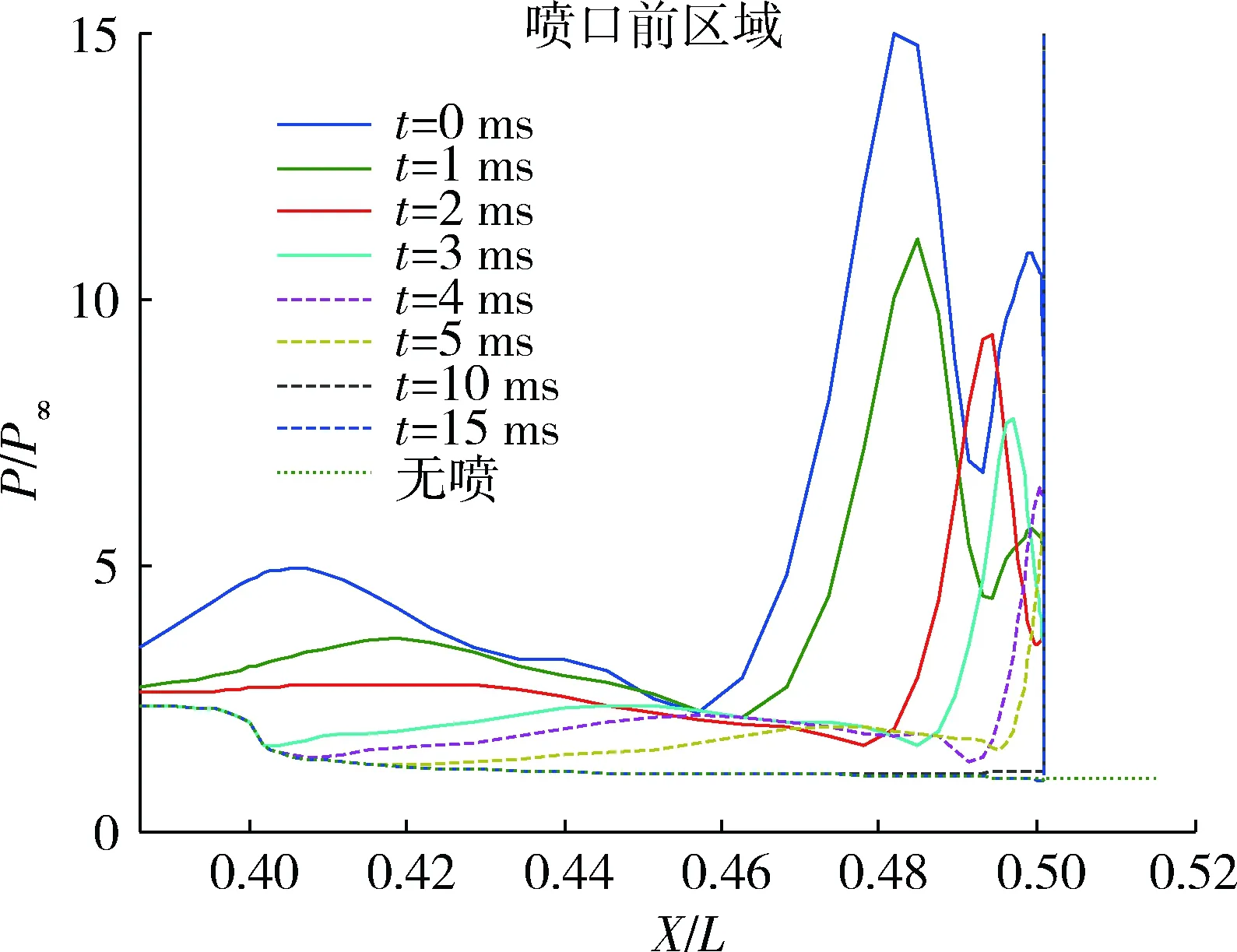
圖11 噴口前區域壓力分布(噴流關閉)Fig.11 Pressure distribution in front of nozzle (jet off)

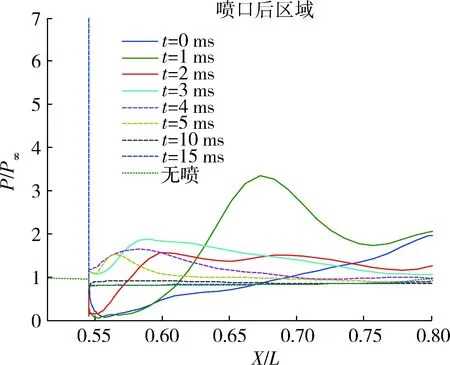
圖12 噴口后區域壓力分布(噴流關閉)Fig.12 Pressure distribution in rear end of nozzle (jet off)

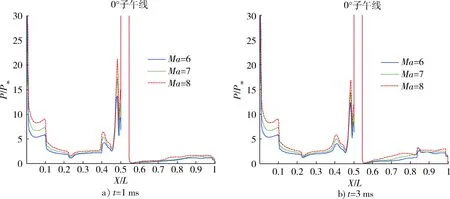
圖13 不同馬赫數條件下壓力分布曲線Fig.13 Pressure distribution under different mach numbers

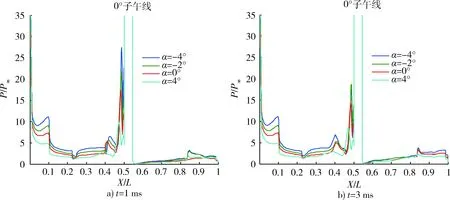
圖14 不同攻角條件下壓力分布曲線Fig.14 Pressure distribution under different angles

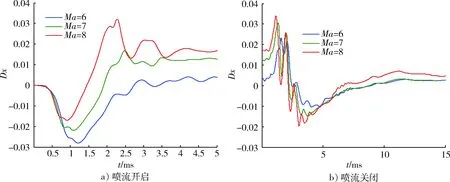
圖15 不同馬赫數條件下推力作用點相對質心的相對偏移量隨時間變化曲線Fig.15 Position offset of point of thrust under different mach numbers

圖16給出了不同攻角條件下推力作用點相對質心的相對偏移量隨時間變化曲線。可以看出，來流攻角≥0°時，噴流開啟后，在0～1.5 ms或0～2.0 ms時，推力作用點相對質心向前偏移，其中在1～1.2 ms向前偏移量最大，之后推力作用點相對質心向后偏移并逐漸趨于穩定；攻角<0°時，噴流開啟后，推力作用點相對質心持續向前偏移并趨于穩定，至1 ms附近向前偏移量最大；噴流關閉0～10 ms內，噴流干擾的影響仍然存在，且噴流進行不穩定擺動，造成推力作用點相對質心也進行不規則偏移，至13 ms左右，推力作用點相對質心偏移量逐漸趨于穩定。

3 結束語

本文采用數值模擬技術對側向噴流非定常干擾效應進行研究，為總體及控制設計提供參考。主要研究結論如下：

(1) 通過多狀態對比分析，給出了適用于此側向噴流問題的非定常數值計算方法，給出了合理的內迭代收斂判據、物理時間步長等。

(2) 噴流啟動后，在1.5 ms時，噴流強度和高度達到最大，但此時激波不穩定，進行不穩定擺動；至5 ms時，噴流干擾流場完全建立并達到穩定狀態

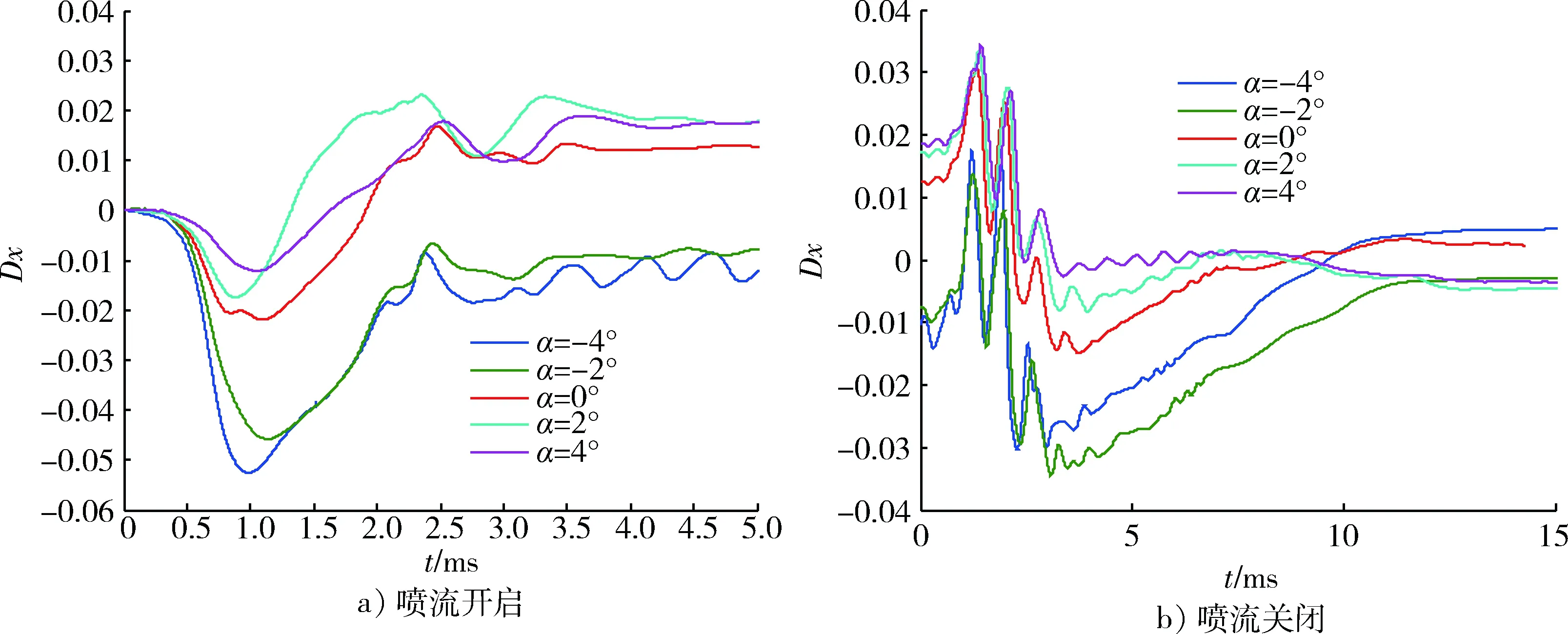
圖16 不同攻角條件下推力作用點相對質心的相對偏移量隨時間變化曲線Fig.16 Position offset of point of thrust under different angles

。

(3) 噴流關閉后，噴流前方弓形激波的強度和高度迅速減小，噴流影響區也迅速減小，至10 ms時，噴流干擾影響基本消退。

(4) 噴流關閉后，存在氣流粘性產生的延遲效應，造成噴流干擾流場在發動機關閉后較長時間才能恢復到穩態。

(5) 飛行參數對噴流干擾影響區及壓力分布等均有明顯影響。

[1] 薄靖龍.側向控制噴流非定常干擾效應研究[D].北京：中國航天空氣動力技術研究院，2013：1-58. BO Jing-long.Investigation of Unsteady Lateral Jet Interaction[D].Beijing：China Academy of Aerospace Aerodynamics，2013：1-58.

[2] 陳堅強，張毅鋒，江定武，等.側向多噴口干擾復雜流動數值模擬研究[J].力學學報，2008，40(6)：735-743. CHEN Jiang-qiang，ZHANG Yi-feng，JIANG Ding-wu，et al.Numerical Simulation of Complex Flow with Mutil Lateral Jets Interactions[J].Chinese Journal of Theoretical and Applied Mechanics，2008，40(6)：735-743.

[3] CASSEL L A.Applying Jet Interaction Technology[J].Journal of Spacecraft and Rockets，2003，40(4)：523-537.

[4] 楊彥廣，劉君.高超聲速主流中橫向噴流干擾非定常特性研究[J].空氣動力學學報，2004，22(3)：295-301. YANG Yan-guang，LIU Jun.Unsteady Characteristic Research of Lateral Jet in Hypersonic External Flow[J].Acta Aerodynamica Sinica，2004，22(3)：295-301.

[5] Takanashi Shinichiro，Sentoh Etsuroh，Yoshida Akihiko，et al.Sidejet Aerodynamics Interaction Effect of the Missile，Part1-Estimation of Missile Sidejet Interaction Force by Modeling in Pressure field[R].AIAA 98-4273.

[6] Kikumoto Kousuke，Sentoh Etsuroh，Takanashi Shinichiro，et al.Sidejet Aerodynamics Interaction Effect of the Missile，Part3-Flight Test Results[R].AIAA 98-4347.

[7] JAMESON A.Time Dependent Calculations Using Multigrid，with Applications to Unsteady Flows Past Airfoils and Wings[R].AIAA-1991-1596，1991.

[8] 趙慧勇，樂嘉陵.雙時間步方法的應用分析[J].計算物理，2008，25(3)：253-258. ZHAO Hui-yong，LE Jia-ling.Application Analysis on Dual-Time Stepping[J].Chinese Journal of Computational Physics，2008，25(3)：253-258.

[9] Rumsey Christopher L，Sanetrik Mark D，Biedron Robert T，et al.Efficiency and Accuracy of Time-Accurate Turbulent Navier-Stokes Computations[R].AIAA-1995-1835，1995.

[10] Ebrahimi Houshang B.Numerical Investigation of Jet Interaction in a Supersonic Freestream[J].AIAA 2005-4866，2005.

[11] 徐筠，徐翔，王志堅，等.多噴口噴流對側向噴流流場影響的風洞試驗研究[J].實驗流體力學，2012，26(5)：13-16. XU Yun，XU Xiang，WANG Zhi-jian，et al.Experimental Investigation on Multi-Jet Interference[J].Journal of Experiments in Fluid Mechanics，2012，26(5)：13-16.

[12] 徐敏，陳剛，陳志敏，等.側向脈沖噴流瞬態干擾流場探討[J].推進技術，2005，26(2)：120-124. XU Min，CHEN Gang，CHEN Zhi-min，et al.Observation of Transient Interaction of Lateral Impulse Jet[J].Journal of Propulsion Technology，2005，26(2)：120-124.

[13] 蔣勝矩，王建，劉萬剛，等.導彈脈沖噴流矢量控制中的氣動干擾數值模擬[J].彈箭與制導學報，2010，30(1)：173-175. JIANG Sheng-ju，WANG Jian，LIU Wan-gang，et al.Numerical Simulation of Aerodynamic Effect of Missile Lateral Impulse Jet Control[J].Journal of Projectiles，Rockets，Missiles and Guidance，2010，30(1)：173- 175.

[14] 劉君，楊彥廣.帶有橫噴控制的導彈非定常流場數值模擬[J].空氣動力學學報，2005，23(1)：25-28. LIU Jun，YANG Yan-guang.Numerical Simulation of Lateral Jet Control Induced by Impulse Rocket Motor for a Supersonic Missile[J].Acta Aerodynamica Sinica，2005，23(1)：25-28.

[15] 喬陽，劉勇，徐敏，等.基于多塊對接網格的多側噴流瞬態干擾特性研究[J].固體火箭技術，2007，30(2)：98-101. QIAO Yang，LIU Yong，XU Min，et al.Research on Transient Interaction Characteristics of Multi-Lateral Jet Based on Multi-Block Butt-Joint Grids[J].Journal of Solid Rocket Technology，2007，30(2)：98-101.

Numerical Investigation of Unsteady Lateral Jet Interaction

REN Shu-jie，CHEN Gang，LIU Yong-li，ZHANG Qing-bing

(Beijing Institute of Electronic System Engineering，Beijing 100854，China)

A numerical simulation method is used for the investigation of unsteady lateral jet interaction. Through many comparisons of the wall pressure distribution，the numerical simulation method suitable for this case is established，which is used to obtain the transient jet interaction flowfield when the jet is on or off. The results show that：①if the jet is on, after 1.5 ms，the intensity and height of jet reaches its peak，but the shock wave is unstable, and the jet interaction flowfield achieves the finally state in 5 ms; ②if the jet is off，the intensity and height of the shock wave and the influence area of jet descend quickly. Due to the delayed effect of air viscosity, in 10 ms time, the influence of jet interference is faded away.

lateral jet；unsteady；dual-time stepping method；jet on；jet off；pressure distribution

2016-09-05；

2016-12-20

有

任淑杰(1985-)，女，河北衡水人。工程師，碩士，研究方向為計算流體力學。

通信地址：100854 北京市142信箱30分箱 E-mail：zgjdrsj@126.com

10.3969/j.issn.1009-086x.2017.03.028

U475.4；V233.7

A

1009-086X(2017)-03-0179-07