二維隨機介質中的聲波輻射傳輸蒙特卡洛數值模擬及應用

孟祥翠，王尚旭，唐跟陽，劉志遠

1 中國石油大學(北京)CNPC物探重點實驗室, 北京 102249 2 中國石油大學(北京)油氣資源與探測國家重點實驗室, 北京 102249 3 中國石化石油勘探開發研究院, 北京 100083

石油地球物理

二維隨機介質中的聲波輻射傳輸蒙特卡洛數值模擬及應用

孟祥翠1,2*，王尚旭1,2，唐跟陽1,2，劉志遠3

1 中國石油大學(北京)CNPC物探重點實驗室, 北京 102249 2 中國石油大學(北京)油氣資源與探測國家重點實驗室, 北京 102249 3 中國石化石油勘探開發研究院, 北京 100083

為了模擬富含小尺度非均質體的勘探區內地震波能量的變化，本文將天然地震中的輻射傳輸理論引入到地震勘探頻段內，給出了基于Born散射系數的二維聲波輻射傳輸方程，并介紹了蒙特卡洛數值模擬的思路。為了檢驗基于Born散射系數的聲波輻射傳輸蒙特卡洛方法的正確性和實用性，將輻射傳輸蒙特卡洛模擬的結果與聲波方程有限差分模擬的結果進行對比。結果表明，輻射傳輸蒙特卡洛模擬的結果與聲波有限差分模擬的結果基本吻合。同時，相比于聲波方程有限差分數值模擬，輻射傳輸蒙特卡洛模擬的計算成本遠小于聲波有限差分數值模擬。因此，對于復雜的非均質儲層，輻射傳輸蒙特卡洛模擬是一種有效的地震散射波能量建模方法。而且，對于物理模型實驗觀測到的地震散射波的數據，我們采用基于輻射傳輸蒙特卡洛模擬的網格掃描方法來估算非均勻介質的統計參數－相關長度和擾動強度。計算結果與物理模型的真實值基本吻合，表明輻射傳輸蒙特卡洛模擬可以被用來估算非均質儲層的統計參數。

Born散射系數；隨機介質；輻射傳輸理論；蒙特卡洛模擬

0 引言

長期以來，油氣地震勘探都以層狀介質模型為基礎，但是現在勘探開發的重點逐漸轉向復雜的非均質儲層，例如復雜砂體構造區、碳酸鹽巖孔洞區以及火山巖區。地質上常用基于數學統計理論的隨機模型來描述該類非均質儲層[1-3]。地震波在該類介質中傳播時，會發生多次散射，產生Coda波(也叫地震尾波)。由于多次散射形成的Coda波的相位是隨機的，在傳統的地震數據處理中，Coda波一般被視為噪聲。但是，研究表明散射波的包絡(即散射波的能量)與隨機介質屬性密切相關[4-5]。可以利用散射波包絡的變化，來反演隨機介質的屬性參量[6-9]，例如非均質體的特征長度(表征非均質體大小)和擾動強度(表征非均質體速度變化程度)。因此，準確地描述隨機介質中的散射波能量的變化至關重要。

在天然地震中，有很多理論來描述地震波能量在隨機介質中的傳播，例如：波動方程有限差分數值模擬法[10]，擴散理論[11-12]，Markov近似法[13]等。目前，最常用的是輻射傳輸理論，輻射傳輸理論忽略散射波的相位信息，考慮地震波能量在空間時間上的變化。輻射傳輸方程可以準確的從波動方程中推導出來。早期，出于簡便的考慮，一般假設散射是各向同性的[14-15]，在這種情況下，可以直接得到解析解。但是，各向同性散射的假設，只能解釋Coda的產生，不能準確的描述地震波脈沖展寬的現象；隨后，引入了各向異性散射系數[16]。各向異性散射下的輻射傳輸方程無法得到解析解，一般采用蒙特卡洛數值模擬法來求解[17-19]。蒙特卡洛模擬法的引入，使輻射傳輸理論更加簡便實用。

本文將天然地震中的輻射傳輸理論引入地震勘探頻段。首先，介紹了基于Born散射系數的聲波輻射傳輸方程以及蒙特卡洛數值模擬的基本思想。接著，給出地震勘探中常用的高斯隨機模型和指數隨機模型各自對應的4個例子，用輻射傳輸蒙特卡洛數值方法模擬地震波能量的變化。為了檢驗基于Born散射系數的聲波輻射傳輸蒙特卡洛方法的正確性和實用性，將輻射傳輸蒙特卡洛模擬結果與聲波方程有限差模擬結果進行對比。最后，采用基于輻射傳輸蒙特卡洛數值模擬的網格掃描方法，從物理模型實驗采集到的地震散射數據來反演模型樣品的統計參數。

1 聲波輻射傳輸理論

1.1 隨機介質

隨機介質模型由大、小兩種尺度的非均勻性組成。大尺度非均勻性描述介質的背景特性，用速度或密度的平均值表示；小尺度非均勻性則是加在背景模型上的隨機擾動，用密度或速度的擾動表示。當隨機過程是平穩的，隨機介質可以通過速度擾動的自相關函數以及對應的功率譜密度函數來表征。常用的兩種隨機介質模型是高斯型隨機模型和指數型隨機模型。二維各向同性高斯型和指數型隨機模型對應的自相關函數和功率譜密度函數分別是：

1)二維高斯型隨機模型

自相關函數：

功率譜密度函數：

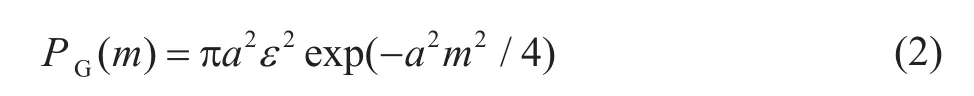
其中，a是相關長度,ε是擾動強度，m是波數。

2)二維指數型隨機模型

自相關函數：

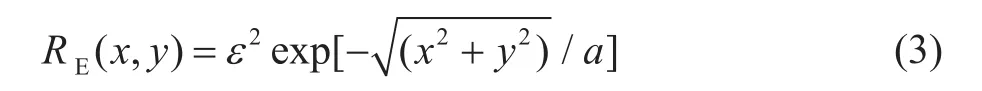
功率譜密度函數：

為了減少獨立的介質參數的個數，根據Birch法則，速度和密度擾動表示為：

v0和ρ0是平均速度和平均密度，δv和δρ是速度和密度擾動，υ=0.8[20]。

1.2 聲波輻射傳輸方程

輻射傳輸方程描述了地震波在隨機介質中傳播時其能量的變化規律，可以由波動方程嚴格推導出來[21-24]。二維聲波輻射傳輸方程可以表示為[20]：

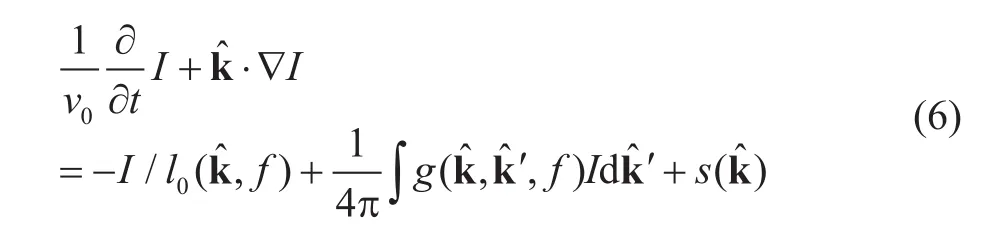
對于方程(6)中的散射系數，可選用從Born近似中導出的單散射系數[19], 二維情況下：

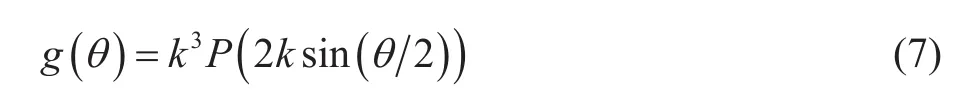
指數型隨機模型對應的散射系數：

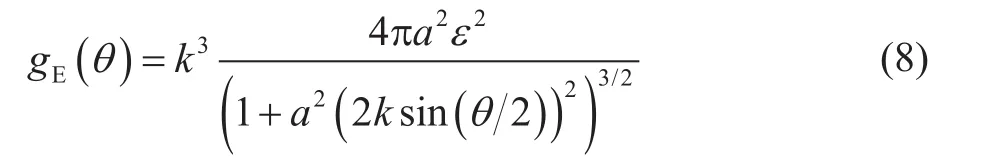
高斯型隨機模型對應的散射系數：

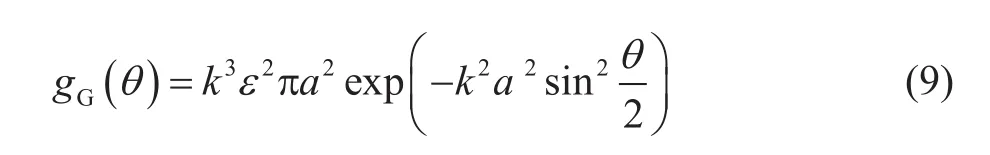
全散射系數可以通過對散射系數進行積分獲得：

高斯型隨機介質全散射系數為：

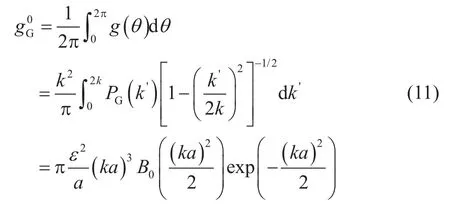
B0是修正的第一類貝塞爾函數，0表示零階。

指數型隨機介質全散射系數為：

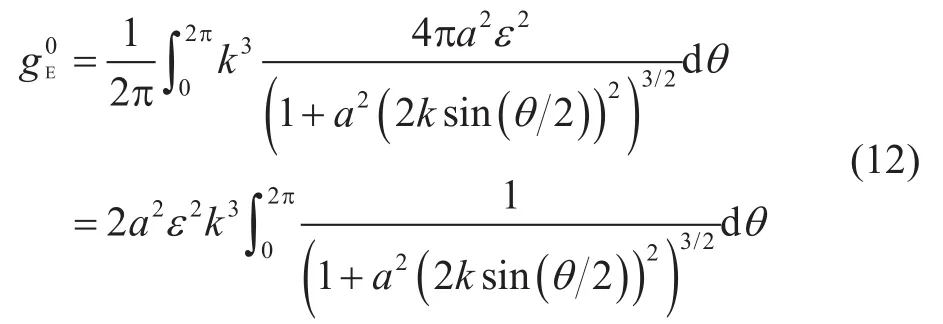
1.3 蒙特卡洛模擬

一般采用蒙特卡洛模擬的方法來求解方程 (6)。Wegler和Yoshimoto詳細介紹了蒙特卡洛模擬的算法[18-19]。蒙特卡洛方法求解輻射傳輸方程的基本思想是：通過大量的粒子運動來描述能量的傳輸過程。首先，在源的位置，向任意方向發射大量的粒子，每個粒子都代表一個單位能量，粒子沿一定方向以速度0v運動。然后，當粒子運動到一定距離時會發生散射，該運動距離是由散射自由程(全散射系數的倒數)來控制；當發生散射時，粒子的運動方向會發生改變，散射角度是由歸一化的Born散射系數來確定。如果介質是多層的，粒子運動到界面時，在界面是發生反射還是透射是根據平均反射和透射能量系數來確定的。在粒子的運動過程中，記錄每個粒子的運動軌跡。最后，統計在t時刻經過接收點R處的粒子數，即可求得能量強度。

2 輻射傳輸蒙特卡洛數值模擬和波動方程有限差分模擬結果對比

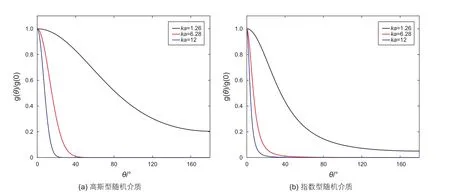
圖1 歸一化的散射系數g(θ)/ g(0)隨散射角θ的變化Fig. 1 The normalized scattering coeff i cient g(θ)/ g(0) varies with scattering angle θ

本文分別選用兩種隨機介質模型：高斯型隨機模型和指數型隨機模型[25-29]。隨機介質建模時，參數如表1所示，模型的背景速度v0=3 000 m/s，ε分別選ε=5%和ε=15%，非均質體特征長度分別選20 m和100 m。隨機模型的縱橫尺寸分別為8 000 m和8 000 m，中心放炮，空間采樣間隔dx=dy=1 m，時間采樣間隔為dt=0.1 ms，傳播時間為3 s，震源子波選用雷克子波，主頻是30 Hz。采用時間二階和空間四階交錯網格差分格式來模擬隨機非均勻介質中的地震波場，在模型上下左右都采用PML吸收邊界條件。記錄距離震源分別為1 500 m和3 000 m的圓上的地震波場，在每個圓上都設置72個等間距的接收點，如圖2所示。

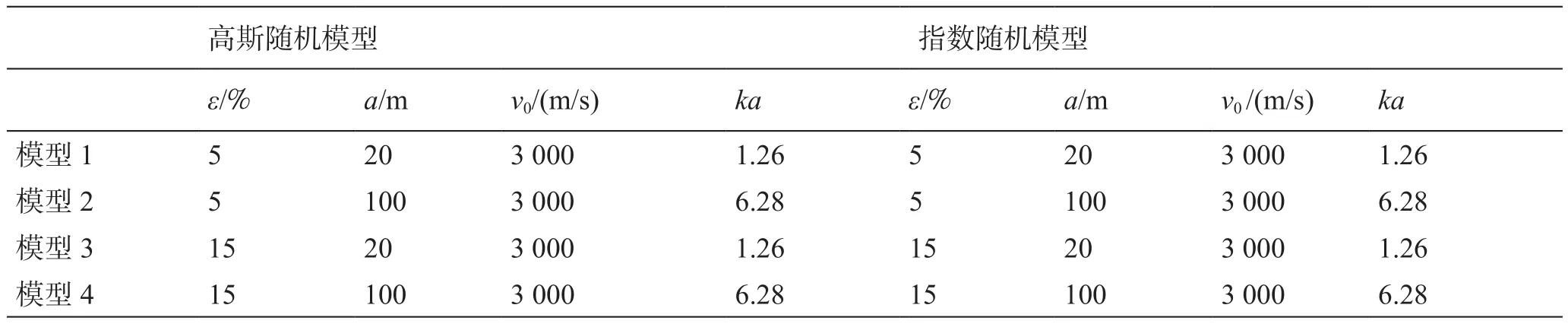
表1 隨機模型參數Table 1 Parameters for random models

波動方程有限差分模擬的是應力場在空間時間上的變化，輻射傳輸蒙特卡洛模擬是能量在時間空間上的變化，為了將有限差分結果和輻射傳輸蒙特卡洛結果相比較，需要對有限差分模擬的地震波場求均方(MS)包絡。求取均方包絡的方法如下：對共炮檢距道集的每一道求平方，再對所有道求和取平均，最后以某一時間窗口進行圓滑得到包絡。另外，有限差分模擬時采用的震源是有一定延展時間的雷克子波，輻射傳輸蒙特卡洛模擬相當于震源是點脈沖震源，考慮到這點，還需要對輻射傳輸蒙特卡洛的結果進行處理：對雷克子波求其平方，然后將輻射傳輸蒙特卡洛的結果與雷克子波取平方的結果求卷積。最后，用均勻介質1 500 m處接收得到的包絡對處理后的輻射傳輸蒙特卡洛結果和波動方程有限差分包絡進行歸一化。

圖3是ε為5%的高斯隨機介質蒙特卡洛輻射傳輸蒙特卡洛的結果和波動方程有限差分結果對比圖，左圖是a=100 m，分別在1 500 m和3 000 m處接收到的結果，右圖是a=20 m，分別在1 500 m和3 000 m處接收的結果。不論是寬角散射還是前向散射，輻射傳輸蒙特卡洛模擬結果和波動方程有限差分計算的結果都吻合的比較好；而且，輻射傳輸方法可以比較準確的描述初至時間、前面直達波包絡的展寬現象以及后面尾波能量的變化。圖4是ε為15%的高斯隨機介質輻射傳輸蒙特卡洛模擬結果和波動方程有限差分結果對比圖。可以看到，輻射傳輸方法和聲波有限差分方法得到的散射波的包絡也基本吻合，只是前面部分有些許偏差。圖5和圖6是指數隨機介質時，蒙特卡洛輻射傳輸結果和波動方程有限差分結果對比圖，比較結果與高斯隨機介質模型類似。

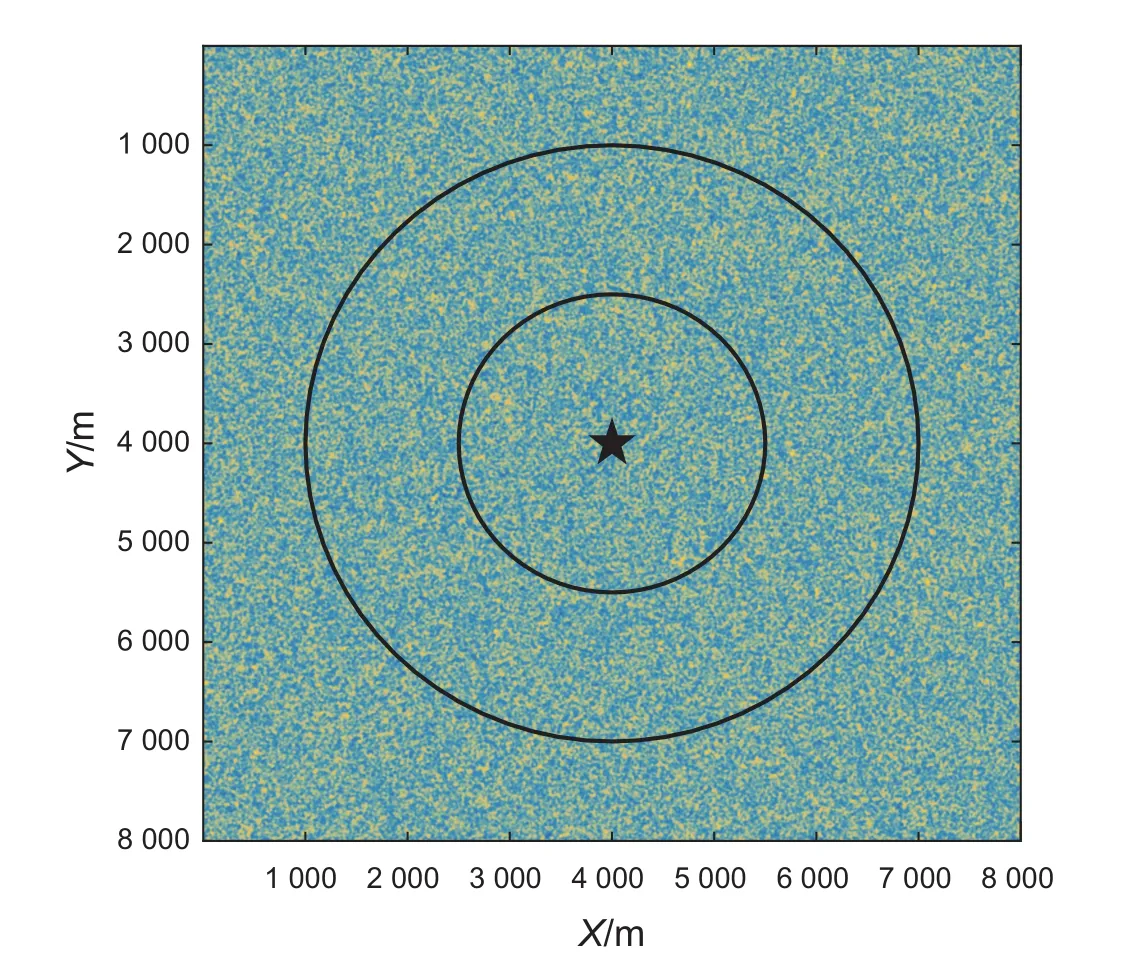
圖2 有限差分模型，縱橫長度8 000×8 000 m。源在中心位置，分別在距離震源1 500 m和3 000 m的圓上接收，每個圓上包含72個等間距的接收點Fig. 2 A fi nite difference model with 8 000 m times 8 000 m grid. The source is located in the center and receivers are distributed along circles with radius 1 500 m and 3 000 m

圖7是4個指數隨機模型(見表1)，分別在1 500 m處接收，采用輻射傳輸蒙特卡洛模擬和波動方程有限差分模擬用時的比較。可以看到，相比于寬角散射(ka=1.26)，前向散射輻射(ka=6.28)輻射傳輸蒙特卡洛模擬用時增加很多，這主要是由于當ka比較大時，散射發生時散射角度主要集中在0o，我們采用取舍法來選擇散射角度則會比較費時[19]。但是，無論是寬角散射還是前向散射情況，聲波輻射傳輸蒙特卡洛模擬計算所需時間遠小于隨機介質聲波方程有限差分數值模擬的計算所需時間。

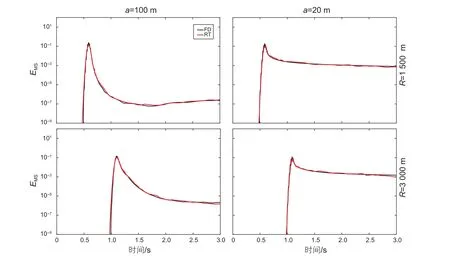
圖3 高斯隨機介質模型，不同參數取值時兩種方法結果的對比。左圖是ε=5%，a=100 m 分別在R=1 500 m(上圖)和=3000 m (下圖)接收時波動方程有限差分包絡(黑線)和輻射傳輸結果(紅線)的對比，右圖是ε=5%，a=20 m 分別在R=1 500 m(上圖)和R=3 000 m(下圖)接收時波動方程有限差分包絡(黑線)和輻射傳輸結果(紅線)的對比Fig. 3 Numerical solutions for 2-D equation of radiative transfer (red) in comparison to numerical solutions of the acoustic wave equation (black) for Gaussian random medium with standard deviation of velocity fl uctuation ε=5%. Correlation distances of the random medium are a=100 m (left) and a=20 m (right). Source receiver distance are R=1 500 m (top) and R=3 000 m (bottom)

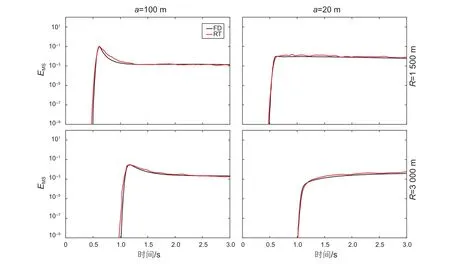
圖4 高斯隨機介質模型，ε=15%，其它與圖3類似Fig. 4 Same as Fig. 3 for Gaussian random medium but with ε=15%

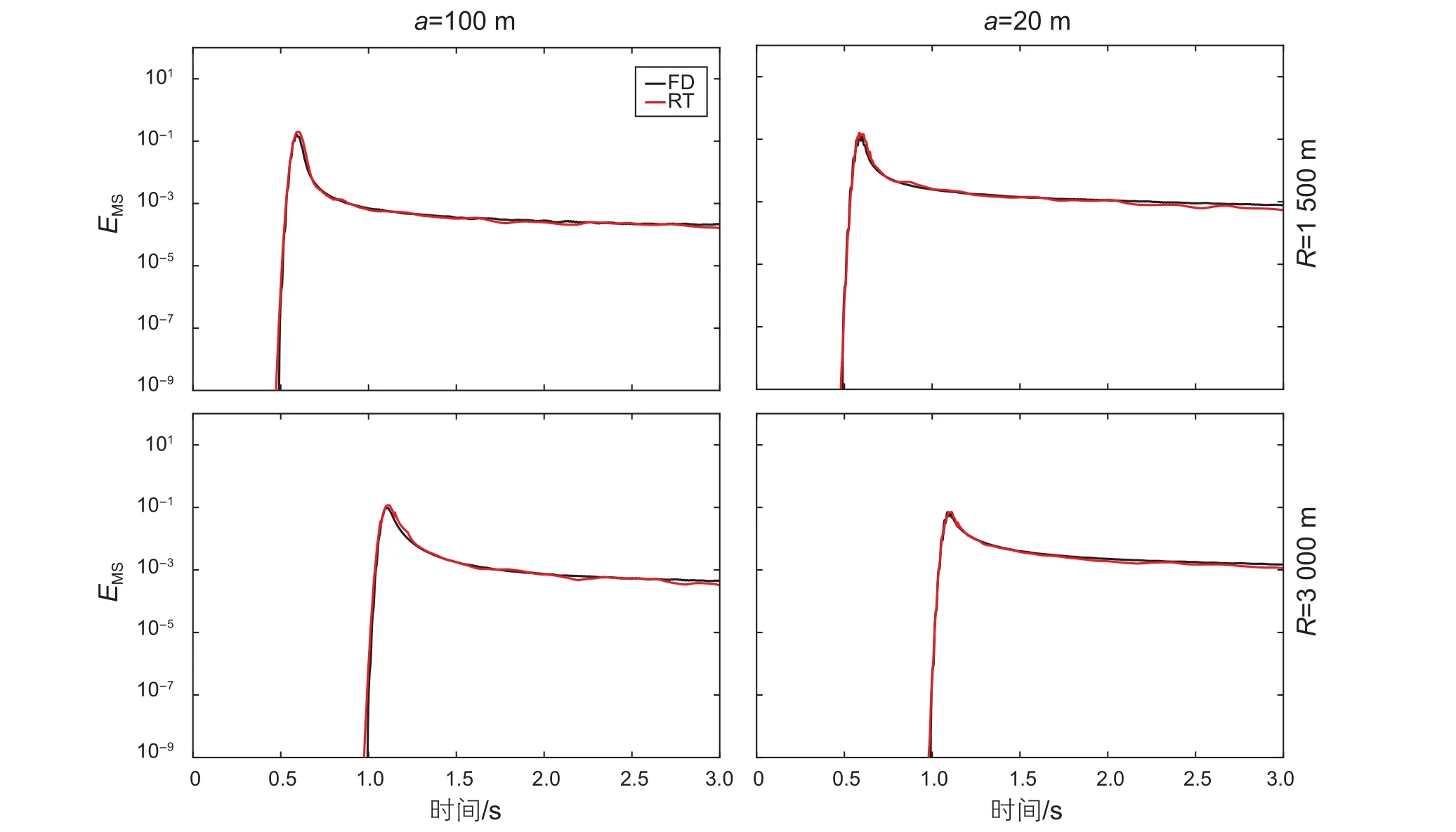
圖5 指數介質模型，不同參數取值時兩種方法結果的對比。左圖是ε=5%，a=100 m分別在R=1 500 m和R=3 000 m接收時波動方程有限差分包絡(黑色)和輻射傳輸結果(紅色)的對比，右圖是ε=5%，a=20 m分別在R=1 500 m和R=3 000 m接收時波動方程有限差分包絡(黑色)和輻射傳輸結果(紅色)的對比Fig. 5 Numerical solutions for 2-D equation of radiative transfer (red) in comparison to numerical solution of the acoustic wave equation (black) for exponent random medium with standard deviation of velocity fl uctuation ε=5%. Correlation distances of the random medium are a=100 m (left) and a=20 m (right). Source receiver distance are R=1 500 m (top) and R=3 000 m (bottom).

圖6 指數隨機介質模型，ε=15%，其它與圖5類似Fig. 6 Same as Fig. 5 for exponent random medium but with ε=15%

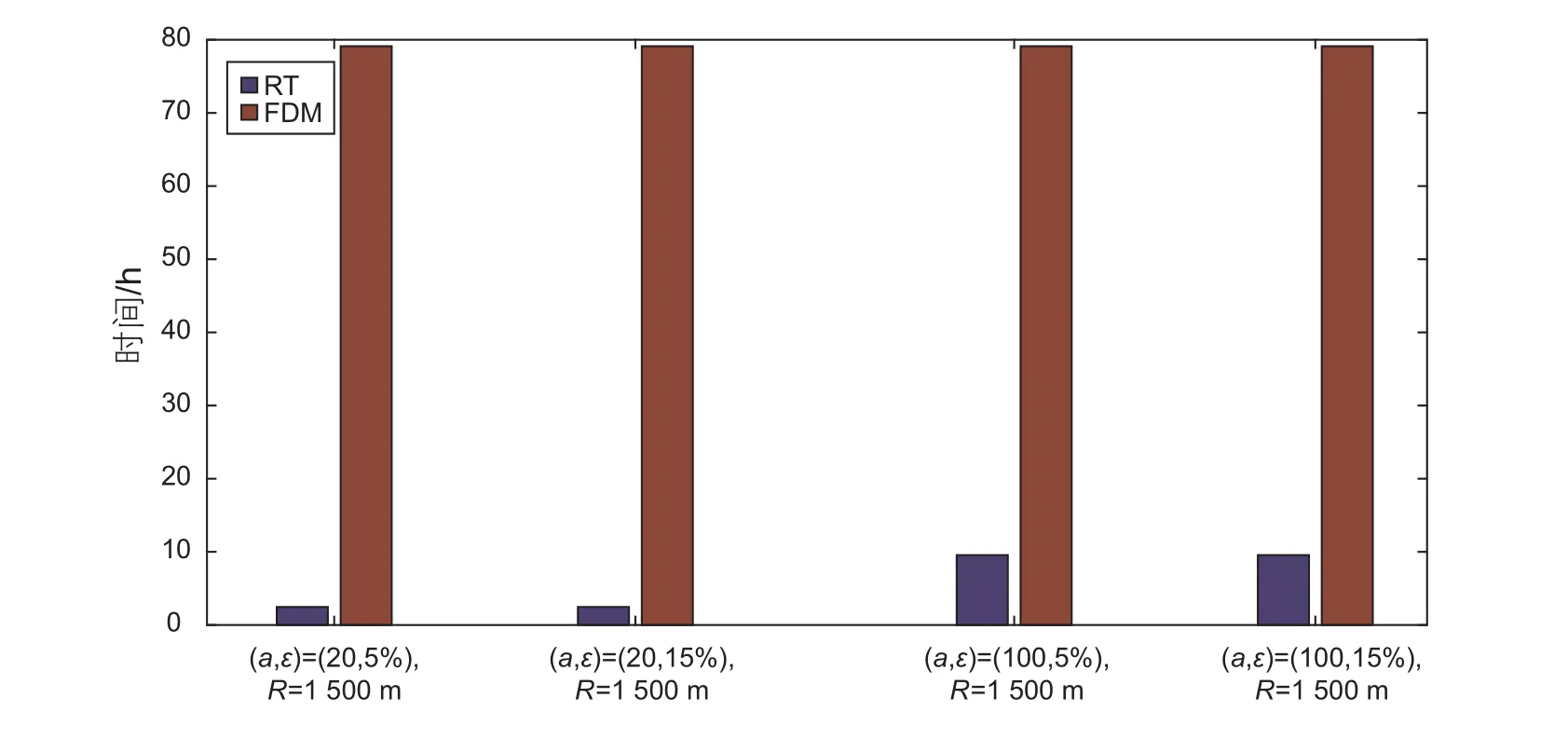
圖7 指數介質隨機模型：模型1、模型2、模型3以及模型4，分別在1 500 m處接收時，輻射傳輸模擬(RT)和波動方程有限差分模擬(FDM)用時比較,其中蒙特卡洛模擬時發射的震源粒子數為1 000 000Fig. 7 Times for 2-D equation of radiative transfer simulation (RT) in comparison to that for the acoustic wave equation fi nite difference method (FDM) for exponent random models (model 1, model 2, model 3 and model 4). The number of particles used in RT is 1 000 000

3 隨機介質統計參數的估計

從方程(6)可知，當已知地震子波和隨機介質的平均速度時，穿過隨機介質的地震散射波的能量只依賴于介質的統計參數：相關長度a和擾動強度ε。因此，對采集到的地震散射數據，我們可以采用基于輻射傳輸方法的網格掃描方法，來估算隨機介質的相關長度a和擾動強度ε。首先，選定要用的隨機模型的類型，例如高斯隨機模型，給定不同的相關長度a和擾動強度ε的值(不同的隨機模型)；然后，根據輻射傳輸蒙特卡洛方法來計算出不同模型時的地震波能量；最后，將輻射傳輸模擬的結果與采集到的地震波場的包絡進行對比，找出與觀測到的地震波場包絡吻合最好時對應的模型，該模型的相關長度和擾動強度就是隨機介質的統計參數的值。為了評價不同模型輻射傳輸蒙特卡洛模擬的結果與觀測得到的地震波場包絡的吻合程度，我們采用下面的公式：

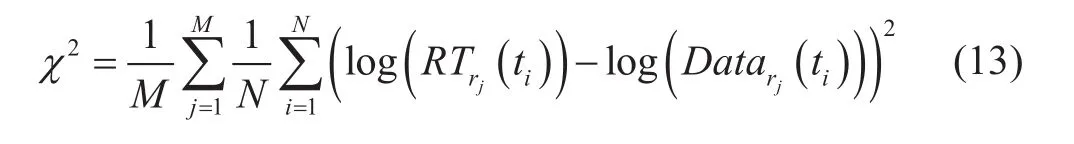
其中，it是時間，N是時間窗口的個數，jr表示第j個接收點，RT是接收點個數。Data是輻射傳輸模擬的結果，是觀測得到的地震波場的包絡。

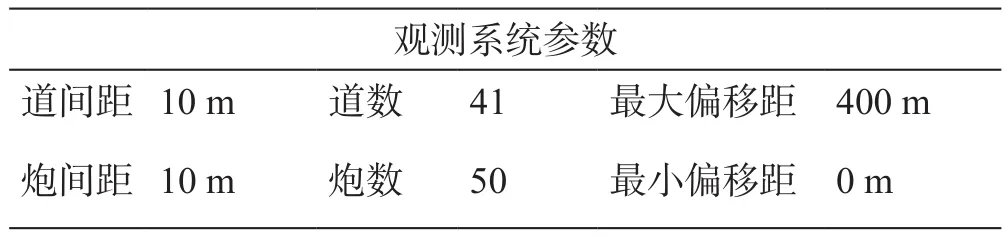
表2 觀測系統參數Table 2 Parameters of seismic observation system

為了分析輻射傳輸蒙特卡洛模擬估算隨機介質統計參數的準確與否，我們用從物理模型實驗采集得到的地震數據來估算介質的統計參數，因為物理模型的基本參數是確定的。隨機模型樣品是選用玻璃珠和環氧樹脂來制作，環氧樹脂作為背景介質，玻璃珠作為非均質體，制作時玻璃珠隨機的分布于環氧樹脂中。隨機模型樣品與野外地質構造尺寸比為1：5 000，即模型1 mm代表野外地質構造的5 m；速度比為1：1。玻璃珠的粒徑為6 mm(野外為30 m)，速度為4 300 m/s。隨機模型樣品是長方體，大小為50×30×5 cm3，即野外隨機介質大小為2 500×1 500×250 m3，圖8b是樣品切面示意圖。模型樣品的平均速度為3 426 m/s,平均密度為 1.9 g/cm3。在水槽中采集透射波場，如圖8a所示，只沿樣品中線采集一條測線，觀測系統參數見表2。震源子波主頻大約是250 kHz(野外為50 Hz)。圖9是第41炮原始地震記錄，可以看到，不僅有直達的P波，P波后面還有明顯的Coda波。我們抽取共偏移距道集，根據前面介紹的方法，求取不同偏移距對應的地震波的包絡，然后做總能量歸一化處理，得到歸一化的地震波包絡，如圖9b所示。

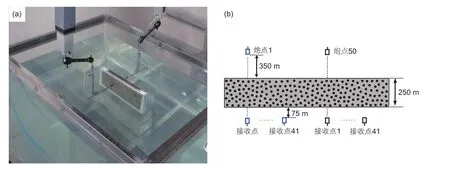
圖8 物理模型實驗示意圖，(a)透射波水槽采集照片；(b) 實驗采集觀測系統示意圖Fig. 8 An illustration of physical model experiments. (a) A photograph of the transmitted wave acquisition modelling system，(b) the transmitted wave experimental conf i guration

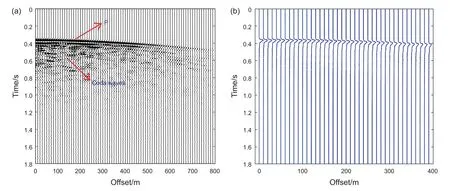
圖9 (a)第41炮原始地震記錄，(b)歸一化的地震包絡隨偏移距的變化情況Fig. 9 (a) The raw common shot gather (shot 41), (b) the normalized envelopes at different offsets

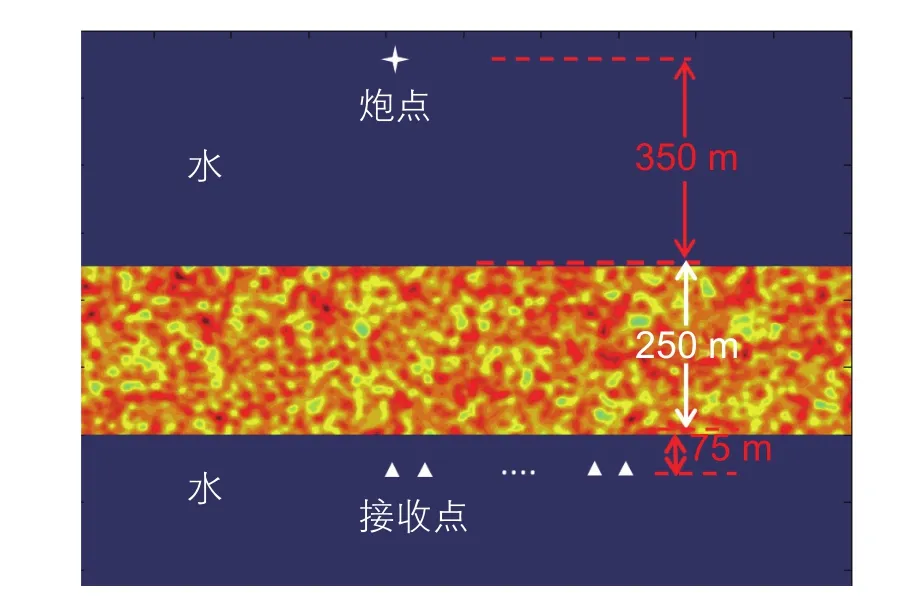
圖10 三層模型以及觀測系統示意圖Fig. 10 The three-layer model and acquisition conf i guration

在進行輻射傳輸蒙特卡洛模擬時，我們選用與物理模型實驗一致的三層模型(圖10)，上層和下層都是水，中間層是非均勻介質。在地球物理中，常用來描述非均勻介質的兩種隨機模型是高斯隨機模型和指數隨機模型；相比而言，高斯隨機模型更加平滑，其非均質體大小比較單一[20]。由于物理模型樣品中的非均質體是玻璃珠，而且粒徑大小基本一樣，所以此處隨機介質模型我們選用高斯隨機模型。高斯隨機模型從(a, ε)=(5, 0.05)變到 (a, ε)=(40, 0.4)，相關長度a以2.5 m的步長從5 m變到40 m，對于每一個相關長度a，擾動強度ε都以0.025的步長從0.05變到0.4。對于這些不同的高斯隨機模型，分別采用輻射傳輸蒙特卡洛模擬計算不同偏移距處的地震波能量的情況，炮點和接收點的相對位置于物理模型實驗一致，如圖10所示。根據公式(13)求取不同模型下輻射傳輸蒙特卡洛模擬的結果與實驗采集得到的地震波包絡的偏差χ，圖11a是χ的等值線圖，可以看到 當(a, ε)=(27.5, 20%) 時，偏差最小。在物理模型實驗中，隨機模型玻璃珠粒徑是30 m，我們通過輻射傳輸方法估算得到相關長度是27.5 m，考慮到相關長度是一個統計值，可以說該結果是正確可信的；模型樣品的平均速度是3 426 m/s, 玻璃珠的速度是 4 300 m/s，速度變化強度大約是 25.5%，估算得到的擾動強度為20%，兩者也基本吻合。

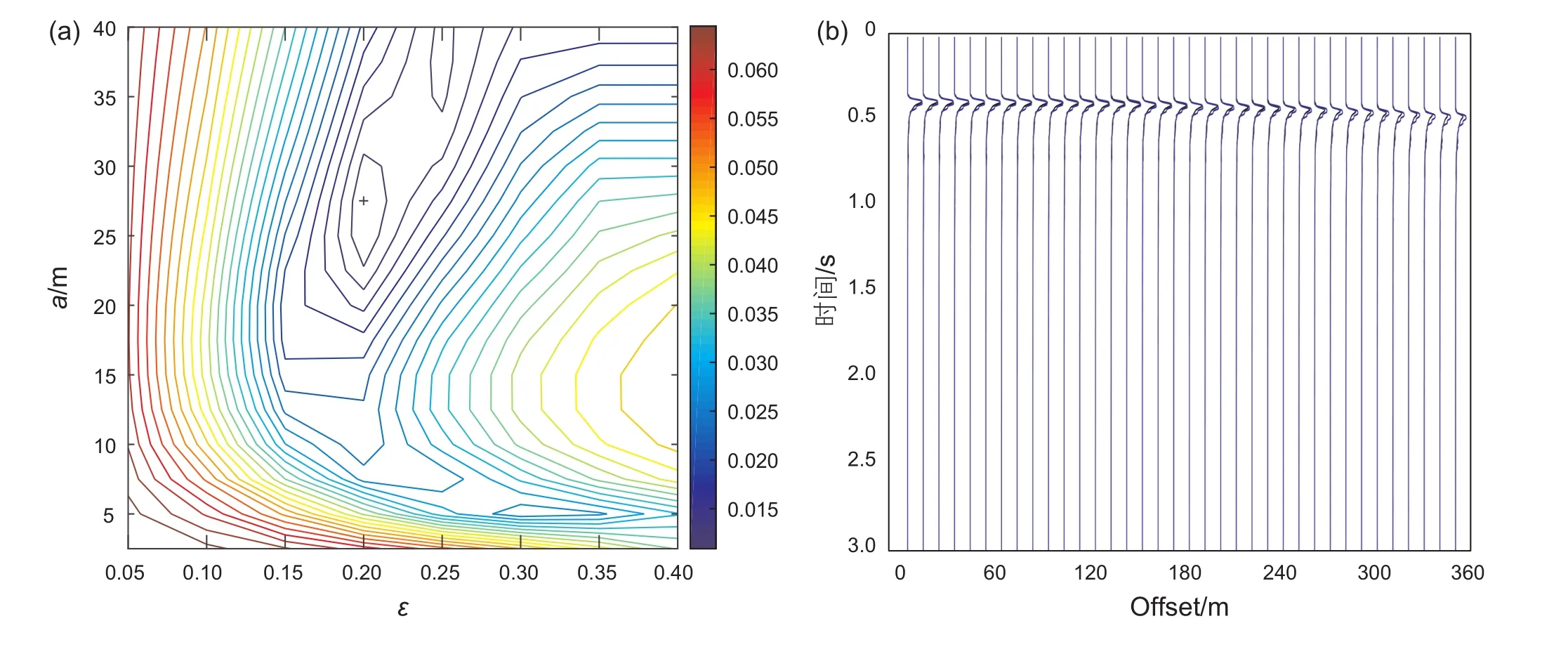
圖11 (a) χ隨(a, ε)變化的等值線圖，(b)(a, ε)=(27.5 , 20%) 對應模型的輻射傳輸模擬結果(藍色)和實驗采集地震波場包絡(黑色)對比圖Fig. 11 (a) The contour plot of χ as a function of (a, ε), (b) Comparisons between the RT results (blue line) with the envelopes computed from the observed data (black line)

4 結論

本文針對常用的高斯隨機模型和指數隨機模型，分別采用基于Born散射系數的輻射傳輸蒙特卡洛方法模擬了寬角散射(ka=1.26)和前向散射(ka=6.28)兩種情況下，速度擾動標準差較小(ε=5%)和較大(ε=15%)時地震波能量的傳輸情況。將輻射傳輸蒙特卡洛計算的結果與聲波方程有限差模擬的結果進行了對比，兩者吻合的比較好，表明輻射傳輸蒙特卡洛數值模擬可以比較準確的描述隨機介質中散射波的能量變化；另外，相比于聲波方程有限差分數值模擬，聲波輻射傳輸蒙特卡洛模擬的計算成本遠小于聲波有限差分數值模擬的計算成本。因此，對于復雜的非均質儲層，輻射傳輸蒙特卡洛模擬是一種有效的地震散射波能量建模方法。對物理模型實驗觀測到的地震散射數據，采用基于輻射傳輸數模擬的網格掃描方法來估算隨機介質的統計參數-相關長度和擾動強度。計算結果與物理模型的真實值吻合較好，說明輻射傳輸蒙特卡洛模擬方法可以用來估算隨機介質的統計參數。

[1] 奚先, 姚姚, 顧漢明. 隨機溶洞介質模型及其波場模擬[J]. 地球物理學進展, 2005, 20(2), 365-369. [XI X, YAO Y, GU H M. Random cavity medium model and the wave fi eld simulation[J]. Progress In Geophysics, 2005, 20(2), 365-369.]

[2] ALMEIDA J A. Stochastic simulation methods for characterization of lithoclasses in carbonate eservoirs[J]. Earth Science Reviews, 2010, 101： 250-270.

[3] KUZNETSOVA A, ALMEIDA J A, LEGOINHA P. Stochastic simulation of the morphology of fluvial sand channel reservoirs[C]. Mathematics of Planet Earth. Berlin： Springer-Verlag, 2014： 689-693.

[4] AKI K. Analysis of the seismic coda of local earthquakes as scattered waves[J]. Journal of Geophysical Research, 1969, 74(2)： 615-631.

[5] AKI K, CHOUET B. Origin of coda waves： source, attenuation, and scattering effects[J]. Journal of Geophysical Research, 1975, 80：3322-3342.

[6] MICHAEL A H, SHEARER P M, EARLE P S. Seismic evidence for small-scale heterogeneity throughout the Earth’s mantle[J]. Nature, 1997, 387： 145-150.

[7] MARGERIN L G, NOLET G. Multiple scattering of high-frequency seismic waves in the deep Earth： PKP precursor analysis and inversion for mantle granularity[J]. Journal of Geophysical Research, 2003, 108(B11)： 2514-2529.

[8] VIDALE J E, EARLE P S. Fine-scale heterogeneity in the Earth’s inner core[J]. Nature, 2000, 404： 273-275.

[9] 王勤彩, 陳章立, ASANO Y等. 利用尾波包絡線反演方法研究伽師強震群區地殼的非均勻結構[J]. 地球物理學報, 2009, 52(1)：90-98. [WANG C Q, CHEN L Z, ASANO Y, et al. Imaging crustal heterogeneity in Jiashi strong earthquake swarm region by coda envelope inversion analysis[J]. Chinese Journal of Geophysics, 2009, 52(1)： 90-98.]

[10] FEHLER M, SATO H, HUANG L J. Envelope broadening of outgoing waves in 2-D random media： A comparison between the Markov approximation and numerical simulation[J]. Bulletin of the Seismological Society of America, 2000, 90(4)： 914-928.

[11] MARGERIN L, CAMPILLO M, TIGGELEN B A. Radiative transfer and diffusion of waves in a layered medium： New insight into coda Q[J]. Geophysical Journal International, 1998, 134(2)： 596-612.

[12] WEGLER U. Diffusion of seismic waves in a thick layer： Theory and application to Vesuvius volcano[J]. Journal of Geophysical Research, 2004, 109(B7)： B07303.

[13] SATO H. Broadening of seismogram envelopes in the randomly inhomogeneous lithosphere based on the parabolic approximation：Southeastern Honshu, Japan[J]. Journal of Geophysical Research, 1989, 94(B12)： 17735-17747.

[14] HOSHIBA M. Simulation of multiple scattered coda wave excitation based on the energy conservation law[J]. Physics of the Earth and Planetary Interiors, 1991, 67(1-2)： 123-136.

[15] ZENG Y, SU F, AKI K. Scattering wave energy propagation in a random isotropic scattering medium-I theory[J]. Journal of Geophysical Research, 1991, 96(B1)： 607-619.

[16] GUSEV A A, ABUBAKIROV I R. Simulated envelopes of non-isotropically scattered body waves as compared to observed ones：Another manifestation of fractal heterogeneity[J]. Geophysical Journal International, 1996, 127(1)： 49-60.

[17] HOSHIBA M. Estimation of non-isotropic scattering in western Japan using coda wave envelopes’ application of a multiple non-isotropic scattering model[J]. Journal of Geophysical Research, 1995, 100(B1)： 645-657.

[18] YOSHIMOTO K. Monte Carlo simulation of seismogram envelopes in scattering media[J]. Journal of Geophysical Research, 2000, 105(B3)： 6453-6161.

[19] WEGLER U, KORN M, PRZYBILLA J. Modeling full seismogram envelopes using radiative transfer theory with born scattering coeff i cients[J]. Pure and Applied Geophysics, 2006, 163(2)： 503-531.

[20] SATO H, FEHLER M, Maeda T. Seismic wave propagation and scattering in the heterogeneous earth[M]. Berlin： Springer-Verlag, 2012. [21] BURRIDGE R, PAPANICOLAOU G C. Transport equations for Stokes’ parameters from Maxwell’s equations in a random medium[J]. Journal of Mathematical Physics, 1975, 16： 2074-2085.

[22] RYTOV S M, KRAVTSOV Y A, TATARSKII V I. Principles of statistical radiophysics 4-Wave propagation through random media[M]. Berlin： Springer-Verlag, 1987.

[23] WEAVER R L. Diffusivity of ultrasound in polycrystals[J]. Journal of the Mechanics and Physics of Solids, 1990, 38(1)： 55-86.

[24] RYZHIK L V, PAPANICOLAOU G C, KELLER J B. Transport equation for elastic and other waves in random medium[J]. Wave Motion, 1996, 24(4)： 327-362.

[25] 奚先, 姚姚. 二維隨機介質及波動方程正演模擬[J]. 石油地球物理勘探, 2001, 36(5)： 546-552. [XI X, YAO Y. 2-D random media and wave equation forward modeling[J]. Oil Geophysical Prospecting, 2001, 36(5)： 546-552.]

[26] 奚先, 姚姚. 二維橫各向同性彈性隨機介質中的波場特征[J]. 地球物理學進, 2004, 19(4)： 924-932. [XI X, YAO Y. The wave fi eld characteristics of 2-D transversely isotropic elastic random medium[J]. Progress in Geophysics, 2004, 19(4)： 924-932.]

[27] 劉永霞, 徐春明, 寧俊瑞. 不同模式自組織介質中聲波傳播特性的比較研究[J]. 地球物理學報, 2007, 50(3)： 830-836. [LIU Y X, XU C M, NING J R. Comparison of acoustic propagation in several different types self-organized media[J]. Chinese Journal of Geophysics, 2007, 50(3)： 830-836.]

[28] 郭乃川, 王尚旭, 董春暉, 等. 地震勘探中小尺度非均勻性的描述及長波長理論[J]. 地球物理學報, 2012, 55(7)： 2385-2401. [GUO N C, WANG S X, DONG C H, et al. Description of small scale inhomogeneities in seismic prospecting and long-wavelength theory[J]. Chinese Journal of Geophysics, 2012, 55(7)： 2385-2401.]

[29] 范小平, 楊從杰, 李清河. 介質非均勻性參數對散射包絡的影響[J]. 地球物理學進展, 2013, 28(2)： 0687-0694. [FAN X P, YANG C J, LI Q H. The effect of inhomogeneity parameters on scattering wave envelopes[J]. Progress in Geophysics, 2013, 28(2)： 0687-0694.]

Monte-Carlo radiative transfer simulation of acoustic waves in two-dimensional random media and it’s application

MENG Xiangcui1,2, WANG Shangxu1,2, TANG Genyang1,2, LIU Zhiyuan3
1 CNPC Key Lab of Geophysical exploration, China University of Petroleum-Beijing, Beijing 102249, China 2 State Key Laboratory of Petroleum Resource and Prospecting, China University of Petroleum-Beijing, Beijing 102249, China 3 Sinopec Petroleum Exploration and Production Research Institute, Beijing 100083, China

In order to describe seismic energy transport in exploration fi elds full of small-scale heterogeneities, the acoustic radiative transfer theory in seismology is introduced into frequency zones of seismic exploration. In this paper, the acoustic radiative transfer theory based on Born scattering coeff i cients in 2-D random media are given, and the Monte-Carlo simulation is brief l y presented to solve the radiative transfer equation. In order to verify the radiative transfer method, Monte-Carlo solutions of the radiative transfer equation are compared with finite difference solutions of the acoustic wave equation, and we find a good coincidence of the two theories. Meanwhile, the Monte-Carlo radiative transfer simulation costs less time than the fi nite difference simulation of acoustic wave equations. Thus, it is a good option to apply Monte-Carlo radiative transfer simulation to model the energy transport of seismic scattering waves in complex heterogeneous reservoirs. Furthermore, we use a grid search procedure based on Monte-Carlo radiative transfer simulation to infer the stochastic parameters - the correlation length and the fl uctuation strength from the observed seismic scattering data acquired in the physical experiment. The estimated results agree with the true values of the physical sample, which indicate that the Monte-Carlo radiative transfer simulation can be used to invert the stochastic parameters of heterogeneous reservoirs.

Born scattering coeff i cient; random medium; radiative transfer theory; Monte-Carlo simulation

10.3969/j.issn.2096-1693.2017.02.019

(編輯 付娟娟)

孟祥翠, 王尚旭, 唐跟陽, 劉志遠. 二維隨機介質中的聲波輻射傳輸蒙特卡洛數值模擬及應用. 石油科學通報, 2017, 02： 199-209

MENG Xiangcui, WANG Shangxu, TANG Genyang, LIU Zhiyuan. Monte-Carlo radiative transfer simulation of acoustic waves in two-dimensional random media and it’s application. Petroleum Science Bulletin, 2017, 02： 199-209.doi：10.3969/ j.issn.2096-1693.2017.02.019

*通信作者, mengxiangcui35105@163.com

2016-11-23

國家重點基礎研究發展計劃項目(2013CB228600)以及國家自然科學基金(41304042)共同資助