一種基于帶權無向圖的中醫方劑頻繁項集挖掘算法

譚 龍 秦琦冰

(黑龍江大學計算機科學技術學院 黑龍江 哈爾濱 150080)

一種基于帶權無向圖的中醫方劑頻繁項集挖掘算法

譚 龍 秦琦冰

(黑龍江大學計算機科學技術學院 黑龍江 哈爾濱 150080)

根據中醫方劑數據的特點，將頻繁項集發現算法應用到中醫方劑的研究中，挖掘治療消渴病胃火熾盛癥型的方劑中不同藥對之間的關聯規則以及核心藥物組合，提出一種基于帶權的無向頻繁項集圖的挖掘算法。該算法可以快速挖掘頻繁k-items(k≥3)，并隨之快速回溯頻繁項集所對應的方劑，從而完成了中醫方劑數據特點的快速數據挖掘。通過實驗表明，該算法避免產生大量候選項集，提高了中醫方劑數據挖掘效率，對完成中醫消渴病方劑信息的用藥規律分析具有重要意義。

消渴病 頻繁項集 無向圖 中醫方劑 數據挖掘

0 引 言

數據挖掘是數據庫知識發現領域內非常熱點的研究方向，主要目的是從大量的數據庫中檢索出用戶感興趣的信息[1]。在數據挖掘中，關聯規則的挖掘是其核心任務之一，其根本意義在于從大量數據中挖掘出項集之間的相互關系。關聯規則分析方面代表性案例就是“購物籃分析”，該案例是通過挖掘顧客購買商品的交易數據，來發現不同商品在交易過程中隱藏的關系，從而獲得銷售的增益[2]。大量研究人員已經在挖掘頻繁項集的算法中作了許多工作，Agrawal等人提出的Apriori的算法是一種最經典的挖掘頻繁項集的算法，在此基礎上，也提出了許多基于Apriori的改進算法，如HEA[3]、MTR-FMA[4]、Modified Apriori[5]以及Improved Aprori[6]等算法，Han等于2000年提出的FP-Growth算法也在頻繁項集挖掘中做出了突出貢獻。

同時，針對基于圖存儲的頻繁項集挖掘方法的研究也引起了很多學者的關注，Yen等人第一次提出了基于有向圖存儲的頻繁項集挖掘算法，文獻[7]又對上述算法進行了改進。在此基礎上，Kumar等提出了一種FIG(Frequent Item Graph)的算法[8]；Tiwari等在FP-Growth的基礎上進行改進，提出了FP-Growth-Graph來進行頻繁項集挖掘[9]。

上述頻繁項集挖掘的算法中，大致可以分為兩個關鍵思路：(1) 產生候選頻繁項集以及進行剪枝。(2) 不產生候選頻繁項集的方法[10]。在頻繁項集挖掘的過程中，方法(1)可能會產生大量的候選項集，增加算法的時間和空間復雜度，而方法(2)避免了候選項集的產生，但是往往需要大量的額外開銷，挖掘效率有待于進一步提高。本文所提出的算法主要遵循方法(2)中思路進行。

本研究團隊一直從事研究中醫方劑中治療消渴病方劑的數據挖掘工作。消渴病是以多飲、多食、多尿、身體消瘦，或尿濁、尿中有甜味為主要表現的一種臨床常見病、多發病，嚴重危害著人類的健康[11]，中醫對于消渴病的預防和治療有著豐富而且獨特的經驗[12]，因此，對《中醫方劑大辭典》中收錄的治療消渴病胃火熾盛癥型的方劑研究也尤為重要。在研究中發現，治療該癥型的方劑中往往存在大量的頻繁的k-items(k≥3)，而相比于頻繁1-items、頻繁2-items而言，頻繁k-items(k≥3)的產生對于治療消渴病胃火熾盛癥型也更具有重要的臨床參考價值。

同時，在對方劑數據庫的頻繁項集挖掘過程中，傳統算法在找到頻繁項集結果后，卻不能有效發現該頻繁項集所對應的方劑名稱，而方劑名稱和頻繁項集的對應關系，對方劑規律分析具有重要意義。因此，本文提出了一種基于帶權的無向頻繁項集圖WUFIG(WeightedUndirectedFrequentItemsGraph)挖掘算法來挖掘頻繁項集。該算法不僅可以解決上述問題，還大大減少了對原始數據庫的掃描次數，避免產生大量的候選項集，能夠有效的挖掘出頻繁k-items(k≥3)，提高了對于中醫方劑數據挖掘效率。

1 系統模型

本文系統模型為，存在項集I={I1,I2,…,Im}，事務數據庫D={〈TID,T〉|T?I}，TID為代表每一條事務的標識符；T為項的集合。事務數據庫D，將進一步產生帶權的無向頻繁項集圖(如圖1所示)，無向頻繁項集圖的節點為項集I中的項組成，節點項之間如果是頻繁項集，則有一條邊，邊的權值用邊的兩個節點項之間的權重表示。

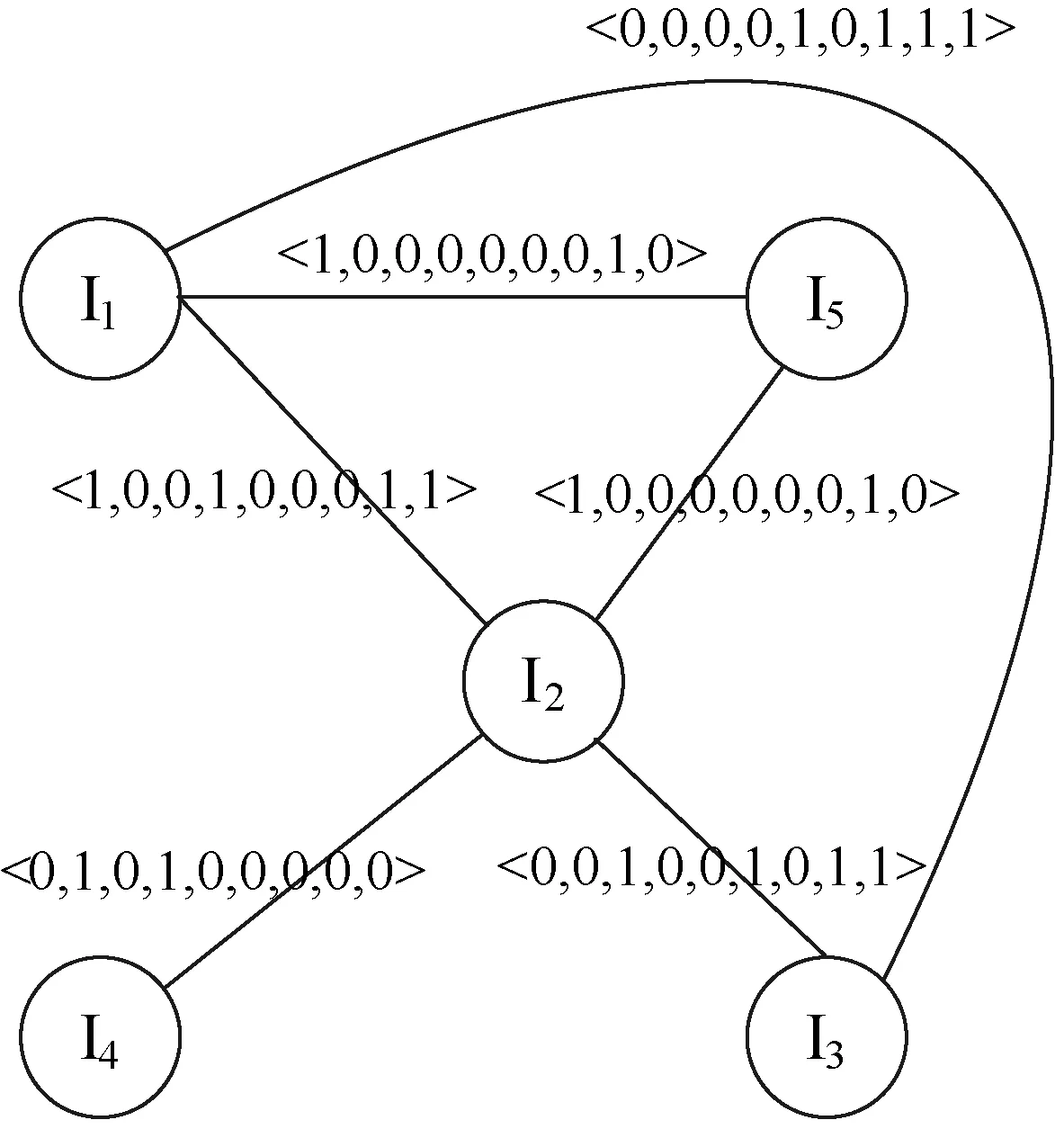
圖1 帶權無向頻繁項集圖

定義1 對于項X，包含所有的X的TID的集合稱之為項X的事務集合，簡稱Tidset，用Tidset(X)表示。

假設TID的個數為n，則Tidset(X)為n位二進制位組成的元組，該元組可存儲在整型Long數據類型(4個字節)中。通常，《中醫方劑大辭典》中收錄的治療常見癥型的方劑約為300首左右，因此，最多需要申請10個Long類型空間存儲事務數據庫中的n位二進制元組，滿足算法的存儲要求。例如，在表1中，n=9，需申請2個Long類型存儲空間(16位)，按照從低位到高位的按位存儲，項I1存在的TID為1，4，7，8，9，則：

Tidset(I1)=<(0,0,0,0,0,0,0,1),(1,1,0,0,1,0,0,1)>

為描述方便，針對表1所示，n=9情況，本文將Tidset(I1)表示為：

Tidset(I1) = <1,0,0,1,0,0,1,1,1>

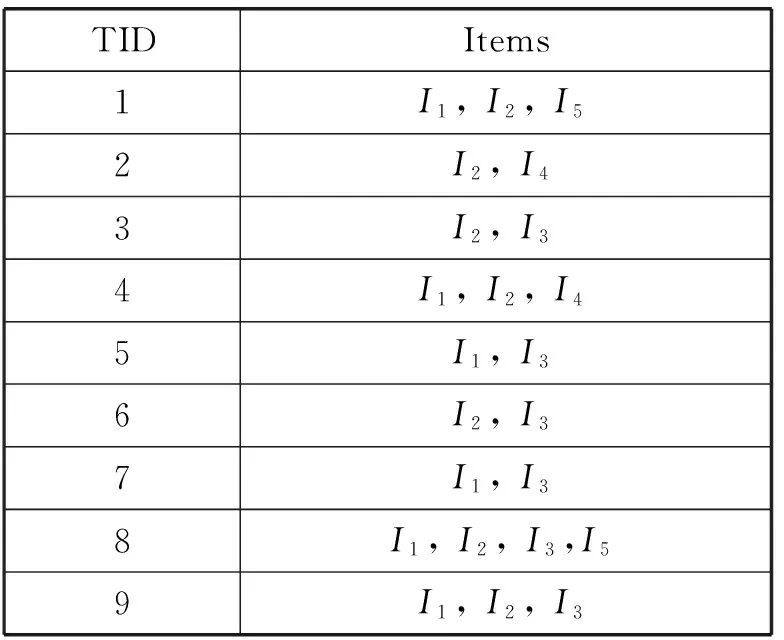
表1 事務數據庫表

定義2 兩個項X和Y之間的Tidset可以進行按位與(&)操作，記為Tidset(X)&Tidset(Y)，其結果與元組一一對應，我們稱該元組為項X與項Y之間的權重，用weight(X,Y)表示。

例如，由定義1可知表1中：

Tidset(I1) = <1,0,0,1,0,0,1,1,1>

Tidset(I2) = <1,1,1,1,0,1,0,1,1>

則：

Tidset(I1)&Tidset(I2)) = <1,0,0,1,0,0,0,1,1>

在帶權的無向頻繁項集圖中，設頻繁1-items為點集V，E為邊集，E(Vx,Vy)表示為點Vx和Vy的邊，minsup為最小支持度閾值，count(Tidset(Vx)&Tidset(Vy))表示Vx和Vy同時出現的次數。由上述定義1和定義2，可得邊權重weight(Vj,Vk)的計算方法為：

?Vi∈L1(1≤i≤m)

?count(Tidset(Vj)&Tidset(Vk))≥minsup則：

E=E∪E(Vj,Vk)

weight(Vj,Vk)=Tidset(Vj)&Tidset(Vk)

在基于帶權的無向頻繁項集圖(WUFIG)中，對于任意兩個頻繁1-items， 如果count(Tidset(X)&Tidset(Y))不小于最小支持閾值，那么X與Y之間存在邊E(X,Y)，該邊加入到E中，同時weight(E(X,Y))為Tidset(X)&Tidset(Y)的結果。

在基于帶權的無向頻繁項集圖(WUFIG)中，對于某個點集合V′中任意兩點Vi和Vk，如果都存在一條邊E(Vi,Vk)E，則V′中所有的點構成一條頻繁項集環，即為頻繁項集。因此，?Vi∈L1(1≤i≤m)，?V′=,如果對于?Vi∈V′，?Vj∈V′，使得E(Vi,Vj)∈E成立，則存在一條頻繁k-items環，該環路經過的頂點即為頻繁k-items。

2 基于帶權的無向頻繁項集圖挖掘算法

本文中提出的算法是基于帶權的無向頻繁項集圖基礎上搜索頻繁k-items環，算法命名為WUFIG(WeightedUndirectedFrequentItemsGraph)。

圖4中，V1、V3、V5分別表示閥1、3、5收到脈沖觸發信號，發生不對稱故障后，由于a相幅值降低，ab換相線電壓過零點超前于對稱故障時的過零點，此時導致實際的觸發角增大，在換相線電壓變為正向時換相結束，因此導致換相失敗。

2.1 算法原理

本算法使用帶權無向圖的方式進行存儲，圖中頂點集合即為頻繁1-items，頂點之間邊的權值即為Tidset(Vi) &Tidset(Vj)，在基于帶權的無向頻繁項集圖(WUFIG)中，如果存在頻繁k-items環，則環上面的頂點即為頻繁k-items。頻繁k-items環路的每條邊的權值，進行與(&)操作，其結果即為頻繁k-items所在的TID。該TID在具體中醫方劑數據處理中，即為頻繁藥物組合所對應的方劑名稱。

無向頻繁項集圖的生成算法見WUFIG_GEN算法，在此無向頻繁項集圖基礎上，搜索頻繁k-items環的操作見Mining_Frequent_K_Items算法，該算法調用Searchfrequentk-itmesloop來完成對頻繁k-items環的搜索。

WUFIG_GEN算法描述如下：

Input：Transactional Database D, minsup

Output: WUFIG

procedure WUFIG_GEN (D, minsup)

1) For each Vj∈L1

2) For each Vi∈L1(i≠j)

3) If (vj∩vi)≠? and count(Tidset(Vj)&Tidset(Vi)) ≥minsup;

4) Add E(Vi,Vi)to Edge set E;

5) Weight(Vi, Vj) = Tidset(Vi)& Tidset(Vj);

6) End if;

7) End for;

8) End for;

End procedure;

Mining_Frequent_K_Items算法描述如下：

Input：WUFIG

Output: frequent k-items,TID

//(k≥3)

Procedure Mining_Frequent_K_Items

//(k≥3)

1) While V≠? do

2) For each Vi, Vj(i≠j) of V

3) If E(Vi, Vj)∈E then

//Vi, Vj之間有邊相連

4) L = Vi∪Vj,V′ = V-{ Vi, Vj}

5) Search frequent k-itmes loop(L,V′);

6) End if;

7) End for;

8) End while;

End procedure;

procedure Search frequent k-itmes loop(L,V′)

1) While V′≠? do

2) For unvisited Vkof V′

3) If E(Vk, ?Vj∈V′)∈E then;

4) L=L∪Vk, V′ = V′-{ Vk};

5) Output L and weight_&;

//輸出頻繁k-items和對應的TID

6) End if;

7) End for;

8) End while;

End procedure;

根據WUFIG_GEN算法，在最小支持度minsup為2的基礎上，首先對事務數據庫D中頻繁1-items的計算Tidset，同時計算任意兩個頻繁1-items的Tidset的交集。

例如，從表1得到：

Tidset(I1) = <1,0,0,1,1,0,1,1,1>

Tidset(I2) = <1,1,1,1,0,1,0,1,1 >

count(Tidset(I1)&Tidset(I2))=count(<1,0,0,1,0,0,0,1,1>)由于count(Tidset(I1)&Tidset(I2))=4>minsup，則I1，I2之間存在一條邊E(V1,V2)。 因此weight(I1,I2) = <1,0,0,1,0,0,0,1,1>，Tidset(I4) = <0,1,0,1,0,0,0,0,0>，count(Tidset(I1)&Tidset(I4) ) =count(<0,1,0,0,0,0,0,0,0>)。由于count(<0,1,0,0,0,0,0,0,0>)=1

根據Mining_Frequent_K_Items算法：對于WUFIG(V,E,W)中?E(Vi,Vj)∈E，例如：圖1中點I1和點I2，從V′=V-{I1,I2}={I3,I4,I5}中選取點I3，則E(I3,I1)∈E，E(I2,I1)∈E，則點I1、點I2和點I3之間存在一條頻繁3-items環，則I1I2I3為頻繁3-items，weight(I1,I2)&weight(I1,I3)&weight(I2,I3) = <0,0,0,0,0,0,0,1,1>，即I1I2I3出現的TID為8，9，同理可以由圖1可以生成頻繁3-itemsI1I2I5，I1I2I5出現的TID為1，8。

2.2 算法復雜性分析

本文提出的基于帶權的無向頻繁項集圖(WUFIG)的頻繁項集挖掘算法，在空間上的耗費主要在于存儲WUFIG中的N個頂點、K條邊以及邊的權重，而存儲WUFIG的復雜度主要取決于事務數據庫的長度。隨著中醫方劑數據庫長度的增大，WUFIG的空間復雜度也會相應的增加，因此，通常的方法是在原始中醫方劑數據的基礎上采用聚類方法，將治療同一癥型的方劑分簇，然后在同一簇內采用該算法進行頻繁項集的挖掘，這樣就可以有效地降低其空間復雜度。

該算法的時間代價主要在于掃描事務數據庫以及搜索頻繁k-items環的過程。掃描事務數據庫所需要的時間取決于事務數據庫的長度，因此這一過程的平均時間復雜度為O(n)；搜索頻繁項集環所需的時間取決于WUFIG中點的個數，V′中點的個數以及頻繁項集的長度，因此這一過程的平均時間復雜度為O(N×K×L)，其中N為V中點的個數，K為V′中點的個數，L為所求頻繁項集的長度。因此總的時間復雜度為O(n)+O(N×K×L)。

3 實 驗

本文的實驗算法使用VC++6.0環境來實現。實驗數據是從《中醫方劑大辭典》中收錄的治療消渴病胃火熾盛方劑中篩選出來的382首方劑，包含218味中藥藥材。

本文中針對于數據的前期準備處理主要是針對藥物組成的規范，該規范包括：藥材的重名和異名處理；同名異方的處理；藥材的計量單位的統一標準。在此規范數據基礎上，構建方劑數據庫。通過對《中醫方劑大辭典》中收錄的方劑進行分析，初步按照編號、方劑名、組成、別名、性、味、歸經、功效等8個屬性進行描述，完成對原始數據庫的構建。從而，利用基于帶權的無向頻繁項集圖(WUFIG)的頻繁項集挖掘算法對數據源存儲的方劑進行分析研究。

3.1 實驗結果

根據本次治療胃火熾盛方劑數量和用到的中藥個數，結合經驗判斷以及不同參數提取數據的預讀，選擇組方中3味藥物核心組合支持度≥20，提取出96個組合，根據提出結果結合經驗判斷，篩選出部分有價值的頻繁3-items以及所對應的方劑名見表2所示。由實驗結果中選擇4味藥物核心組合支持度≥15，提取出67個組合，根據提出結果結合經驗判斷，篩選出部分有價值的頻繁4-items以及對應的方劑名見表3所示。

表2 治療胃火熾盛組方中3個藥物核心組合

表3 治療胃火熾盛組方中4個藥物核心組合

根據對于消渴病胃火熾盛癥型的經驗，藥物關聯規則結果中選擇支持度≥15，置信度≥0.6，去掉相互包含的規則后，同時針對胃火熾盛方劑對得到的結果進行關聯規則分析后得到20條有價值的規則，見表4所示。

表4 胃火熾盛方劑中部分藥物關聯規則

《中醫方劑大辭典》中收載的治療胃火熾盛型消渴病的方劑，分析得到治療胃火熾盛型消渴病的方劑中藥物的使用頻次，選取適合的支持度，提取出治療胃火熾盛型消渴病3 味藥物的核心組合96組、4 味藥物的核心組合67 組，并且進一步揭示了胃火熾盛型消渴病組方中藥物的關聯規則，可以得出以下結論：

(1) 從表2、表3可知，治療胃火熾盛型消渴病方劑中藥物頻次最高的四味藥為黃連、麥冬、天花粉、知母，為醫家基本用藥組合，可作為臨床組方用藥時的重要參考與借鑒。

(2) 通過核心藥對所在的方劑名，可以得到治療胃火熾盛型消渴病的方劑治療時以清胃火為主，同時兼補心、肺、胃、腎等相關臟腑之陰。

(3) 通過以上數據中的用藥頻次與藥物關聯規則可以看出，黃連、麥冬、天花粉、知母四味藥物與石膏、黃芩、黃柏、大黃等藥物的配伍運用亦為治療胃火熾盛型消渴病的常見藥物組合。

3.2 實驗對比分析

本文主要針對FP-Growth、FIG、FP-Graph算法，選擇了minsupthreshold為0.3%、0.25%、0.2%、0.15%、0.1%進行對比實驗。實驗數據通過采用《中醫方劑大辭典》中收錄的治療消渴病胃火熾盛方劑作為基礎數據，采用常用藥材隨機分布的方式，構建了10 000條實驗數據，進行算法性能對比分析。實驗結果如圖2所示。從圖中可以看出，隨著最小支持度閾值的降低，運行時間都在增加，但是基于帶權的無向頻繁項集圖(WUFIG)的頻繁項集挖掘算法的時間增加率要遠低于其他算法。從實驗結果可以得知：基于帶權的無向頻繁項集圖(WUFIG)的頻繁項集挖掘算法的復雜度要優于其他算法。

圖2 基于不同支持度算法對比分析圖

假設minsupthreshold為0.25%，實驗方劑數據量從2 000增加到10 000，進行算法性能的對比實驗。隨著實驗方劑數據量的增加，算法產生的中間候選項集會不斷增大，時間代價也會越來越大。由圖3可知，基于帶權的無向頻繁項集圖(WUFIG)的頻繁項集挖掘算法性能方面優于其他算法。

圖3 基于不同事務數量算法對比分析圖

4 結 語

在對《中醫方劑大辭典》中收載的治療胃火熾盛型消渴病方劑進行研究分析時，針對研究分析數據的特點，提出了一種基于帶權的無向頻繁項集圖(WUFIG)的頻繁項集挖掘算法。該算法能夠有效快速地產生頻繁k-items(k≥3)，并隨之快速回溯頻繁項集所對應的方劑，對于分析該癥型中醫用藥規律的研究有著重要意義。由于該算法只需掃描一次原始數據庫，而且在頻繁項集挖掘過程中，避免產生大量候選項集，降低了時間復雜度，大大提高了算法的效率。同時，隨著事務數據庫的增大，帶權的無向頻繁項集圖邊的權重元組的存儲空間會增加，接下來，我們將針對如何有效地壓縮其存儲空間作進一步研究。

本文算法通過對消渴病方劑數據分析所得到的核心藥物組合以及方劑名稱，在一定程度上反映消渴病胃火熾盛型的用藥規律，可作為在臨床針對消渴病胃火熾盛型的組方用藥時的重要參考與借鑒。在診療疾病的過程中對于臨床醫生的判讀與分析，提供了有效的保證，具有重要的臨床應用價值。

[1] Solanki S K,Patel J T.A survey on association rule mining[C]//Advanced Computing & Communication Technologies (ACCT),2015 Fifth International Conference on.IEEE,2015:212-216.

[2] Girotra M,Nagpal K,Minocha S,et al.Comparative survey on association rule mining algorithms[J].International Journal of Computer Applications,2013,84(10):18-22.

[3] Li Z C,He P L,Lei M.A high efficient AprioriTid algorithm for mining association rule[C]//Machine Learning and Cybernetics,2005 International Conference on.IEEE,2005:1812-1815.

[4] Thevar R E,Krishnamoorthy R.A new approach of modified transaction reduction algorithm for mining frequent itemset[C]//Computer and Information Technology,2008 11th International Conference on.IEEE,2008:1-6.

[5] Abaya S A.Association rule mining based on Apriori algorithm in minimizing candidate generation[J].International Journal of Scientific & Engineering Research,2012,3(7):1-4.

[6] Sunil K S,Shyam K S,Akshay K C,et al.Improved Aprori algorithm based on bottom up approach using probability and matrix[J].International Journal of Computer Science Issues,2012,9(2):242-246.

[7] Yen S J,Chen A L P.A graph-based approach for discovering various types of association rules[J].IEEE Transactions on Knowledge and Data Engineering,2001,13(5):839-845.

[8] Kumar A V S,Wahidabanu R S D.A frequent item graph approach for discovering frequent itemsets[C]//Advanced Computer Theory and Engineering,2008 International Conference on.IEEE,2008:952-956.

[9] Tiwari V,Tiwari V,Gupta S,et al.Association rule mining:a graph based approach for mining frequent itemsets[C]//Networking and Information Technology (ICNIT),2010 International Conference on.IEEE,2010:309-313.

[10] Mohamed M H,Darwieesh M M.Efficient mining frequent itemsets algorithms[J].International Journal of Machine Learning and Cybernetics,2014,5(6):823-833.

[11] 王芳芳.消渴病古代文獻研究及近30年用柴胡類方治療資料的分析[D].廣州:廣州中醫藥大學,2011.

[12] 榮開明.復興中醫藥學的幾點思考[J].湖北中醫藥大學學報,2015,17(2):59-62.

A TRADITIONAL CHINESE MEDICINE PRESCRIPTION FREQUENT ITEM SETS MINING ALGORITHM BASED ON WEIGHTED UNDIRECTED GRAPH

Tan Long Qin Qibing

(CollegeofComputerScienceandTechnology,HeilongjiangUniversity,Harbin150080,Heilongjiang,China)

According to the characteristics of traditional Chinese medicine prescription data, the frequent item sets discovery algorithm is used to the study of TCM prescriptions, and mine the association rule and core drug combination of the different drugs in the prescriptions for the treatment of Emaciation-Thirst disease with stomach fire flaming. In this paper, frequent item sets mining algorithm based on weighted undirected graph is proposed. The proposed algorithm can rapidly mine frequent k-items, and quickly backtrack to the prescription corresponding to frequent item sets, thus accomplishing the rapid data mining of TCM prescription data. Experiments show that this algorithm avoids generating a large number of candidate items and improves the data mining efficiency of TCM prescription, which is of great significance to analyze the law of drug use in the prescriptions of Emaciation-Thirst disease.

Emaciation-Thirst disease Frequent item sets Undirected graph Chinese medicine prescription Data mining

2016-04-05。國家自然科學基金面上項目(81273649)；黑龍江省自然科學基金面上項目(F201434)。譚龍，副教授，主研領域：傳感器網絡，數據挖掘。秦琦冰，碩士生。

TP

ADOI:10.3969/j.issn.1000-386x.2017.05.007