金屬薄片的自適應變形

孫曉鵬 洪靖惠

(遼寧師范大學計算機與信息技術學院 遼寧 大連 116000)

金屬薄片的自適應變形

孫曉鵬 洪靖惠

(遼寧師范大學計算機與信息技術學院 遼寧 大連 116000)

針對金屬薄片通過彎折、沖壓成型等變形過程，提出關于金屬薄片變形的快速、有效的自適應仿真框架。首先基于金屬薄片材料的幾何及物理特性，修改自適應重新網格化的加勁肋約束；并對網格的最佳尺寸約束進行改進，以模擬金屬的高延展性；最后給出簡單高效的金屬薄片自適應變形仿真的系統框架。實驗結果表明，該框架可適用于任何金屬薄殼。

金屬薄片 塑性變形 拉伸彎曲 自適應網格 仿真

0 引 言

對金屬薄片施加外力進行彎折，然后解除，金屬薄片恢復形變的程度非常小。影響因素主要為平面內剛度，它一定程度上代表了受外力作用的材料抵抗變形的能力，而金屬薄片的平面內剛度比普通彈塑性薄片如報紙、樹葉等高出許多。平面內剛度越大，沿著集中變形區域周圍受到的影響區域則比軟性材料更大。在幾何上可以體現為點與點之間力的相互作用更加明顯。另外，金屬相對其他薄片，有一個明顯的特征便是金屬的延展性。因此在自適應網格的過程中我們需要充分考慮到金屬的這一特性。

1 相關工作

自適應網格技術在提高有限元方法精度方面有大量的文獻。在1996年Bossen[1]等提出了一種描述了二維各向異性、非結構三角網格生成的新算法，能夠在復雜的區域產生高質量的網格，但是當該算法接收較低質量的網格時，可能會導致網格不夠平滑。2002年Villard和Borouchaki[2]的工作和2003年Labelle和Shewchuk[3]的研究工作中保證了各向異性網格的質量,但是在三維或者多維的網格下無法保證其適用性。2007年Alliez[4]的工作研究了網格細化應用于圖形問題。近些年來，薄片的變形和彎曲的數學模型也已得到廣泛的發展，比如2003年Grinspun等[5]的簡單離散型薄片仿真，這種薄片結構物體包括帽子、樹葉等，該文中的模型主要特點就是簡單易實現。2015年CC Kao和WC Hsu[5]研究了一種非規則應用的自適應異構運行框架，JGS Paiva、S William Robson等[6]的工作中研究了自動數據分類是一個計算密集型的任務，提出了可變精度和相當敏感的分類配置和數據表示，特別是對不斷變化的數據集，自適應的思想就便是如此。

2 本文研究算法

本文金屬薄片的變形基于紙張的自適應網格更新方法，其基本思想為：根據受力大小和應變大小不斷進行網格重劃分，使得受力變形程度大的區域網格密集，反之，則網格稀疏。具體數據處理流程如圖1所示。

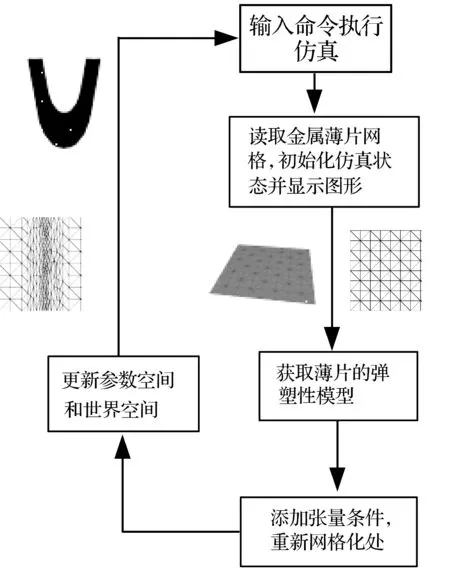
圖1 金屬薄片變形仿真算法幀流程圖

同時，實現了金屬薄片的彎折、通過對重新網格化改進加勁肋約束，給出了若干金屬薄片沖壓模擬實驗。

2.1 應 力

金屬薄片彈塑性模型主要分為兩大部分，幾何模型和物理模型。幾何模型為三角面片組成的有限元網格。參照2008年Eitan Grinspun[7]的幾何模型,在金屬薄片變形前我們定義一個二維的物質參數空間(u,v)，這個參數空間定義了金屬薄片三角面片的每個頂點的位置u，參數空間的點的速度v，與世界空間速度相同。每個頂點同時也擁有三維空間位置，并已知三角面片的幾何拓撲信息。如圖2所示。

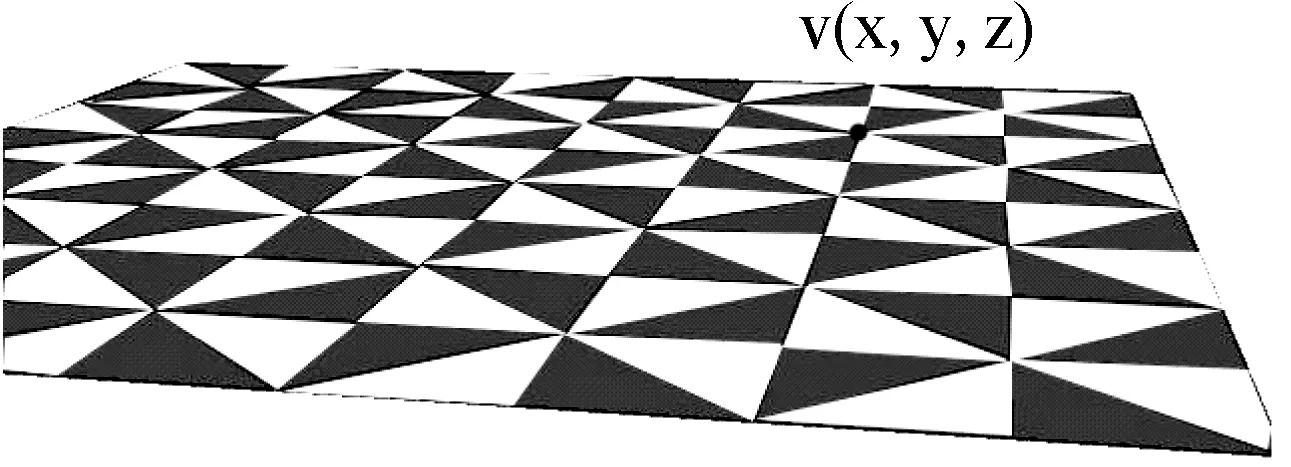
圖2 參數空間和世界空間

本文的物理模型材質為各類金屬片，并定義了實驗金屬對象的表面密度，拉伸剛度系數，彎曲剛度系數，剛度比例阻尼系數，應變條件等。這其中的物理過程涉及到的力主要為局部變形產生兩個應力：拉伸力和彎曲力。

人為給定一個初始力，通過彈簧質點模型來初始化模型物理狀態。我們把應力定義在三角形的面片上。本文以彎折薄片實驗為例進行敘述，初始受力狀態和方向如圖3所示。

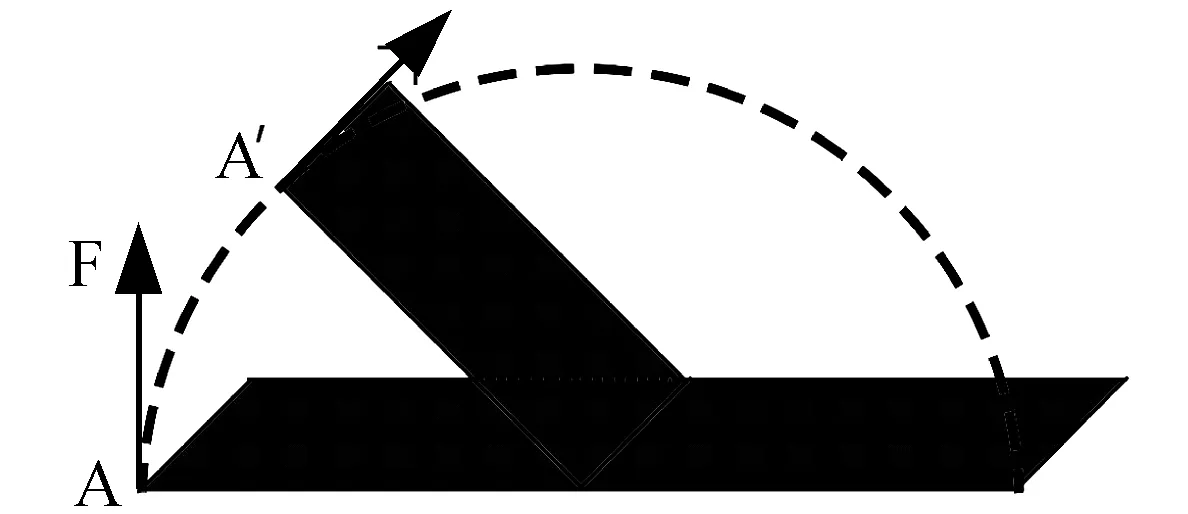
圖3 金屬薄片的折疊受力圖

應力和應變是相輔相成的，通過每個面片上的每一幀的相對應變，來計算整個薄片所有力導致的相對變形的總和，從而更新金屬薄片的新的坐標和幾何狀態。

2.2 應 變

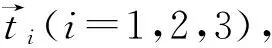
(1)

圖4 變量示意圖

彎曲應變，又可分為塑性彎曲應變和彈性彎曲應變。根據2013年Narain等[9]的應變公式，我們初始化一個2×2的張量E來表示每個面片的總彎曲應變：

(2)這里的le為邊的長度，te為參數空間垂直于邊的單位向量。當彎曲變形發生時，將伴隨著的單元的彈性彎曲應變和塑性彎曲應變，我們假設塑性彎曲應變為初始化為零的2×2張量Ep，則彈性彎曲應變可通過公式：Ee=E-Ep。我們通過以下表達式更新塑性彎曲應變：

(3)

金屬薄片的彈塑性物理模型都是建立在以上討論的膜應變和彎曲應變的基礎上。通過2002年Eitan和Petr等[10]對于離散線性系統的研究可知，所有一維和二維單元都可表示為一個線性系統。我們通過1987年的Terzopoulos[11]使用的歐拉-拉格朗日公式來進行運動方程的求解：

(4)

其中，M分別代表質量矩陣，D為阻尼矩陣，fext表示物體所受外力。V(x)表示物體形狀為x時候的彈性勢能。當我們得到每個單元的變形量和坐標位移量，便可以采用2003年的Grinspun[12]中提到的Newmark方法進行時間離散和幾何模型坐標的更新，從而得到新的薄片形狀。

2.3 自適應網格化

對幾何模型進行重新網格化的目的就是為了能夠夠解決動力學和視覺上的細節問題，并且能夠有效地捕捉到金屬薄片變形的細節：變形較大的區域網格細化，變形較小的地方網格粗化。

1996年Frank[13]在他的研究工作中提到，在黎曼幾何里面，由一個度量張量M定義距離的各向異性，用來衡量度量空間中距離及角度的二階張量。M是一個對稱的2×2的矩陣，不僅可以用來計算幾何中的兩個點的距離、角度，還可以計算三角形面積、三角形剖分等。其中三角剖分在我們的自適應網格劃分中起到了很大的作用，它能夠利用各個條件來限制網格的邊長和大小，從而達到物理解和網格粗細程度耦合的效果。

網格尺寸的物理影響條件為：面片的彎曲性，速度梯度，障礙點和加勁肋。根據2004年Rusinkiewicz等[14]的研究工作中所討論的，速度條件張量：

(5)

根據Narain在2012年[15]的研究工作中提出的障礙點條件，利用以下公式進行計算：

(6)

其中▽為參數空間有限元的梯度計算，di為面的第i個頂點到最近的障礙點向量。

3 加勁肋條件的優化處理

基于物理條件對網格的影響，我們還考慮到，當一個薄片承受壓力，是明顯不可能彎曲到垂直于現有的曲率的，對于金屬薄片則更加明顯。在本文模擬的對象金屬薄片中，我們把加勁肋的作用加在每條三角形的邊上以對金屬抗彎曲性能的加強。我們利用1997年Lobkovsky等[16]對加勁肋的研究工作的基礎上，對公式進行了改進，計算公式如下：

(7)

加勁肋對于邊的作用效果主要體現在不同的彎曲剛度系數kb。我們以條狀薄片為幾何模型做了彎曲實驗，分別采取不同材料，產生如圖5所示的對比效果圖。

圖5 不同材質薄片的彎折仿真效果圖

通過圖5，我們可以觀察到由于紙質薄片材料偏軟，對其進行彎折會產生一處折痕并且主要集中在中間，即網格加密處集中且密集程度大，因其抵抗變形的能力弱。而對于鋁制金屬材料，我們對其加勁肋做了加強處理，使得彎折的效果和網格變化與紙制材料相比產生了明顯的金屬變形特性：不容易在一處集中變形，其彎折也不會產生明顯的折痕，網格也不在一處集中加密。圖6為三種材料彎折后的三視圖。

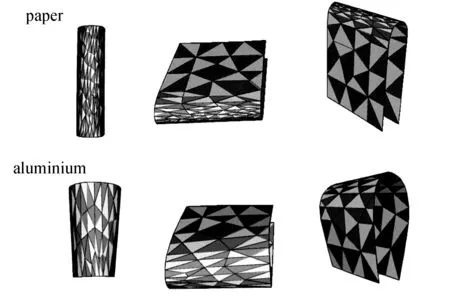
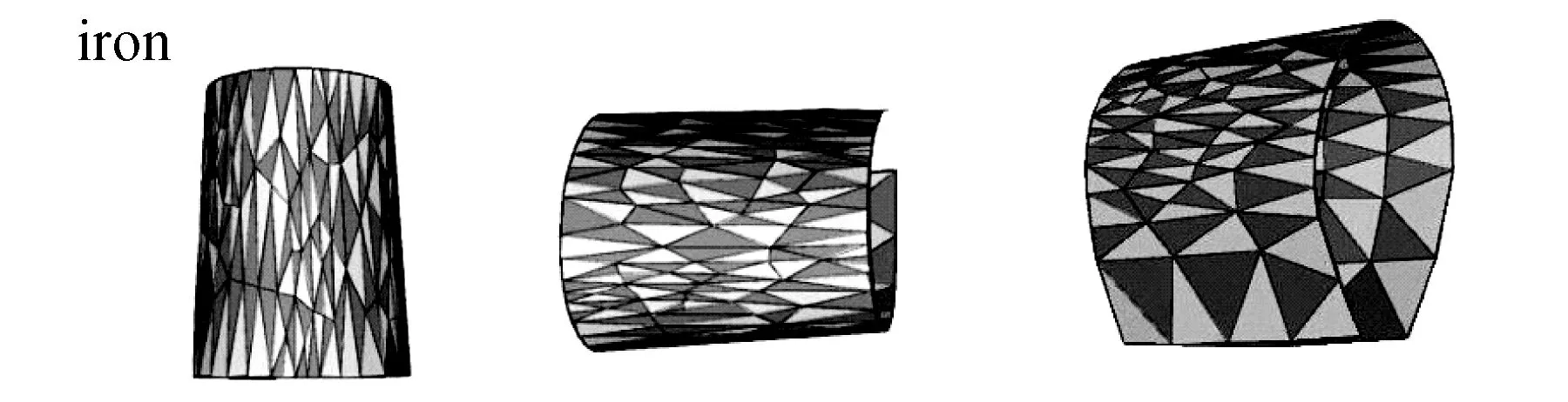
圖6 三種材質薄片彎折三視圖

4 重新網格化的優化處理

(8)

5 實驗結果及分析

本文設計了仿金屬沖壓實驗，利用不同的沖壓模具，如三角板、球、四角板等，使薄片相對于模具以一個較大的初始力快速壓向模具，得到變化如圖7-圖9所示。

圖7 仿角鋼沖壓效果圖

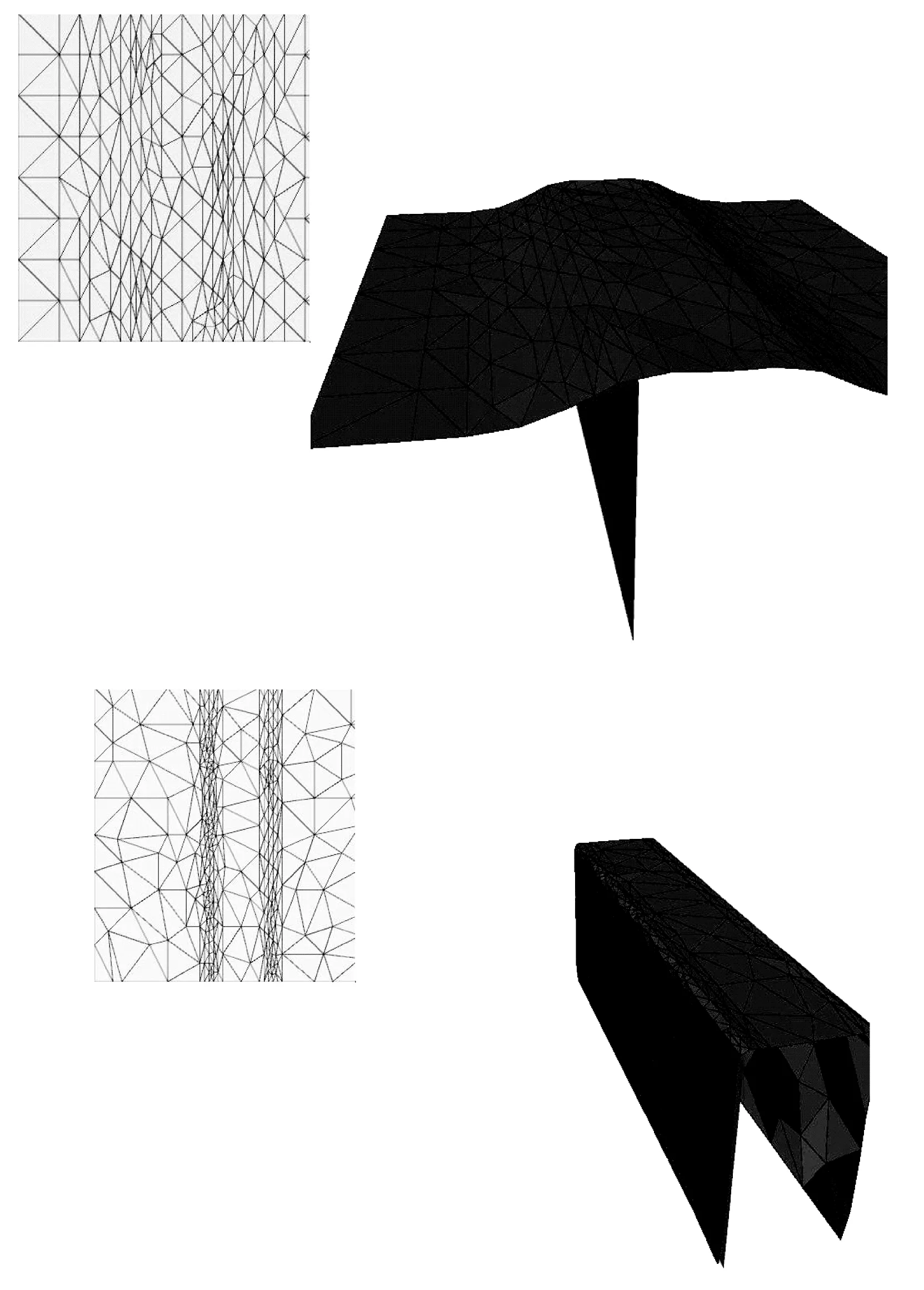
圖8 仿槽鋼沖壓效果圖

圖9 仿易拉罐壓底效果圖

圖10分別為金屬薄片模型的參數空間網格圖、世界空間網格圖，以及渲染成型效果圖。對于上述實驗結果，我們已經從仿真結果圖上得到了部分較好的判斷，但在數據上，我們的評價和分析主要針對其形成的網格質量。為此，我們對幾何模型點數據較龐大的模型的數據抽取將近4 000個點進行網格質量計算，然后把它們分成20個組，第一組為從中隨機抽取100個網格進行計算取平均數，第二組為從中隨機抽取200個網格取平均數……依次類推，我們將這20個組里的每個數據繪制成兩個折線圖，如圖11和圖12所示。

圖10 金衣

圖11 Aspect Ratio統計折線圖

圖12 Edge Ratio統計折線圖

從折線統計圖可以看出，通過隨機抽取的大量網格數值的平均值，結果逐漸趨于平穩，數值逐漸趨近于1，即生成的網格質量接近于優秀。雖然也有不夠優秀的網格產生，但沒有產生不合格的網格。

6 結 語

針對金屬薄片通過彎折、沖壓成型等變形過程，給出了快速、有效的自適應仿真框架。首先基于金屬薄片材料的幾何及物理特性，修改了自適應重新網格化的加勁肋約束。然后對網格的最佳尺寸約束進行了改進，以模擬金屬的高延展性。最后給出了簡單高效的金屬薄片自適應變形仿真的系統框架。

[1] Bossen F, Heckbert P. A pliant method for anisotropic mesh generation [C]// 5th International Meshing Roundtable, Sandia National Laboratories, Washington, DC,October 1996: 63-76.

[2] Villard J, Borouchaki H.Adaptive meshing for cloth animation[C]// Proc.11th International Meshing Roundtable,Springer-Verlag, Washington, DC,2002: 243-252.

[3] Labelle F, Shewchuk J R.Anisotrpic voronoi diagrams and guaranteed-quality anisotropic mesh generation[C]// Proceedings of the nineteenth annual symposium on Computational geometry.San Diego, CA, USA.June 08-10,2003.ACM New York, NY, USA.

[4] Alliez P, Ucelli G, Gotsman C, et al. Recent Advances in Remeshing of Surfaces[M]// Shape Analysis and Structuring. 1970:53-82.

[5] Kao C C, Hsu W C. An Adaptive Heterogeneous Runtime Framework for Irregular Applications[J]. Journal of Signal Processing Systems, 2015, 80(3):1-15.

[6] Paiva J G S, Schwartz W R, Pedrini H, et al. An Approach to Supporting Incremental Visual Data Classification[J]. IEEE Transactions on Visualization & Computer Graphics, 2015, 21(1):4-17.

[7] Grinspun E. A discrete model of thin shells[J]. Oberwolfach Seminars, 2008, 38:325-337.

[8] Gingold Y,Secord A, Han J Y, et al. A discrete model for inelastic deformation ofthin shells[R]. Courant Institute of Mathematical Sciences,New York University.2004.

[9] Narain R, Pfaff T, O’Brien J F. Folding and crumpling adaptive sheets[J]. Acm Transactions on Graphics, 2013, 32(4):51:1-8.

[10] Grinspun E, Krysl P, Schr?der P. CHARMS: a simple framework for adaptive simulation[C]// Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 2002, San Antonio, Texas, Usa, July. 2002:281-290.

[11] Terzopoulos D. Elastically deformable models[C]// Conference on Computer Graphics and Interactive Techniques. 1987:205-214.

[12] Grinspun E, Hirani A N, Desbrun M, et al. Discrete shells[C]// ACM Siggraph/eurographics Symposium on Computer Animation. Eurographics Association, 2003:62-67.

[13] Bossen F.Anisotropic mesh generation with particles[D].CMU-CS-96-134.School of Computer Science Carnegie Mellon University Pittsburgh,1996.

[14] Rusinkiewicz S. Estimating curvatures and their derivatives on triangle meshes[C]// International Symposium on 3d Data Processing, Visualization and Transmission, 2004. 3dpvt 2004. Proceedings. IEEE, 2004:486-493.

[15] Narain R, Samii A, O’Brien J F. Adaptive Anisotropic Remeshing for Cloth Simulation[J]. Acm Transactions on Graphics, 2012, 31(6):147:1-10.

[16] Lobkovsky A E, Witten T A. Properties of Ridges in Elastic Membranes[J]. Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1996, 55(2):1577-1589.

ADAPTIVE DEFORMATION OF SHEET METAL

Sun Xiaopeng Hong Jinghui

(SchoolofComputerandInformationTechnology,LiaoningNormalUniversity,Dalian116000,Liaoning,China)

Aiming at the deformation process of sheet metal by bending and stamping, this paper proposes a fast and effective adaptive simulation framework for sheet metal deformation. Firstly, based on the geometrical and physical properties of the metal foil material, the adaptive re-meshed the stiffening rib restraint is modified. Then, the optimal size constraint of the mesh is modified to simulate the high ductility of the metal. Finally, a simple and efficient system framework for adaptive deformation simulation of sheet metal is presented. The experimental results show that the framework can be applied to any metal shell.

Sheet metal Plastic deformation Stretching bending Adaptive mesh Simulation

2016-04-18。國家自然科學基金項目(60873110)。孫曉鵬，教授，主研領域：計算機圖形學。洪靖惠，碩士生。

TP39

A

10.3969/j.issn.1000-386x.2017.05.012