基于回聲狀態網絡的短期股價預測模型

張 斌

(西南交通大學信息科學與技術學院 四川 成都 610031)

基于回聲狀態網絡的短期股價預測模型

張 斌

(西南交通大學信息科學與技術學院 四川 成都 610031)

針對傳統單只股票預測模型預測精度低以及傳統神經網絡訓練過程復雜的問題，提出一種基于ESN(Echo State Network)的地區行業通用模型，該模型可預測同地區同行業內任意股票。使用ESN建立了上海地區房地產行業的股價預測通用模型，簡化了訓練過程，且與單只股票預測模型相比，該通用模型預測精度明顯提高。在通用模型基礎上提出一種基于數據波動性聚類的KMeans-ESN模型，通過實驗得出:基于ESN的短期股價預測地區行業通用模型適合波動大的數據、基于數據波動性聚類的KMeans-ESN短期股價預測模型適合波動小的數據。

KMeans 回聲狀態網絡 短期股價預測 通用模型 波動性

0 引 言

眾所周知，證券市場在我國的國民經濟發展中起著極其重要的作用，而股票作為一種人們非常熟悉的證券形式，是證券市場的重要組成部分。目前，研究股價預測的學者越來越多。人們相繼提出的分析方法有基本分析、技術分析和時間序列分析等[1]。股票市場是一個非常復雜的系統，其受到經濟、政策以及市場等因素的影響[2]。針對如此復雜的動態非線性系統，許多研究人員采用BP神經網絡進行股票價格預測。

目前，BP神經網絡是用于非線性系統預測的較為常用的方法。但是傳統神經網絡預測模型中存在訓練過程復雜的問題，而且由于股票價格受諸多因素影響，呈現出不同的特點，單一的模型往往難以滿足股票預測需求，同時，大多股價預測模型為單只股票模型，即該模型只包含單只股票信息，并沒有包含與該只股票處于同一地區(考慮到不同地區的相關政策不同，因此將地區限制在同一地區比較合理)同一行業的其余股票信息。而一只股票的價格不僅受該股票所屬公司影響，而且受同一地區同一行業內其余股票公司即競爭者影響，這使得單只股票預測模型不能涵蓋影響單只股票價格的所有因素，導致預測精度不高，預測過程繁瑣復雜。

針對上述存在的問題，本文提出一種基于回聲狀態網絡的地區行業通用短期股價預測模型，并建立上海地區房地產行業通用模型，簡化了訓練過程。模型訓練好后可預測上海地區房地產行業內任意股票，且與單只股票預測模型相比，該行業通用模型的預測精度明顯提高。同時，在通用模型基礎上本文提出了基于數據波動性聚類的KMeans-ESN短期股價預測模型。通過將兩類模型進行實驗對比得出兩類模型各自適用的數據類型，即基于ESN的短期股價預測模型適合波動大的數據、基于數據波動性聚類的KMeans-ESN短期股價預測模型適合波動小的數據。

1 KMeans-ESN模型構建

1.1 KMeans算法

KMeans算法是數據挖掘十大經典算法之一，其基本思想是給定參數K和K個初始聚類中心，計算原始數據與聚類中心的距離(一般使用歐氏距離)，并通過迭代的方式更新聚類中心，直到聚類中心幾乎不再變化，此時將原始數據分為K類，使得類內具有較高相似度，類間具有較低相似度[3]。

假設要將樣本集分為K類，算法步驟如下：

(1) 隨機選擇K個類的初始中心；

(2) 在第i次迭代中，對任意一個樣本，計算其到K個中心的距離，并將樣本歸到距離最短的中心所在的類；

(3) 使用均值等方法更新類的中心值；

(4) 對于所有K個聚類中心，若利用(2)、(3)的迭代法更新后，其值幾乎不再變化或達到最大迭代次數，則迭代結束，否則繼續迭代。

1.2 回聲狀態網絡

回聲狀態網絡ESN的基本思想是通過初始參數的合理設置及網絡初始化動態地產生一個高維非線性空間，使得系統的期望輸出能夠從該非線性空間組合得出。ESN已經在非線性系統辨識、時間序列預測等領域得到廣泛應用。它的很好的短期記憶能力更加使得它在時間序列預測方面成為不二選擇。

ESN是由不來梅雅各布大學教授Herbert Jaeger提出的一種新型遞歸神經網絡算法。他指出遞歸神經網絡在第n時刻的內部狀態x(n)是前n個時刻輸入u(n),u(n-1),…,u(1)的函數，即可將第n時刻的內部狀態理解為歷史輸入的“回聲”[4]。其公式描述如下：

x(n)=E(u(n),u(n-1),…)

(1)

基本回聲狀態網絡結構如圖1所示。

圖1 基本回聲狀態網絡結構圖

基本的回聲狀態網絡結構類似神經網絡，由輸入層，儲備池和輸出層構成。其中，K為輸入節點數，N為儲備池節點數、L為輸出節點數。在n時刻輸入節點的輸入為u(n)=(u1(n),u2(n),…,uK(n)),儲備池的狀態為x(n)=(x1(n),x2(n),…,xN(n)),輸出節點的輸出為y(n)=(y1(n),y2(n),…,yL(n))。從輸入、儲備池到輸出三層之間都有連接。基本回聲狀態網絡結構從輸入節點到輸出節點和輸出節點之間的連接在圖1中用虛線表示。

N+1時刻儲備池的狀態更新方程為：

x(n+1)=f(Winu(n+1)+Wx(n)+Wbacky(n))

(2)

N+1時刻輸出節點的更新方程為：

y(n+1)=fout(Wout(u(n+1),x(n+1),y(n)))

(3)

其中，Win是從輸入節點到內部節點的輸入權值矩陣，大小為N×K，W是儲備池內部節點之間的權值矩陣，大小為N×N。W是一個稀疏矩陣，稀疏度一般為1%～10%[5]。Wout是從輸入節點、內部節點和輸出節點到輸出節點的輸出權值矩陣，大小為L×(K+N+L)，Wback是從輸出節點到內部節點的反饋權值矩陣，大小為N×L。f為儲備池節點的激活函數，fout為輸出節點的激活函數，二者一般均取tanh。

需要注意的是，輸出節點到輸出節點之間的連接幾乎不使用[6]，因此輸出權值矩陣Wout變為從輸入節點、內部節點到輸出節點的權值矩陣，大小為L×(K+N)。這是國內很多學者容易忽視的問題。對應的回聲狀態網絡結構如圖2所示。

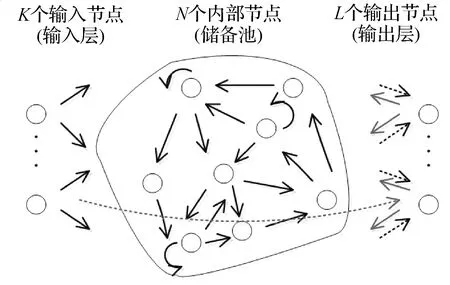
圖2 回聲狀態網絡結構圖

相應的N+1時刻網絡的更新方程為：

x(n+1)=f(Winu(n+1)+Wx(n)+Wbacky(n))

(4)

y(n+1)=fout(Wout(u(n+1),x(n+1)))

(5)

ESN的核心是儲備池。儲備池是由輸入信號所驅動的動態系統。儲備池有兩個功能：(i)可以看做是輸入信號u(n)的高維非線性擴展x(n)；(ii)具有短暫的記憶輸入信號u(n)的功能[7]，也就是回聲狀態。一個好的儲備池同時具有這兩個功能，使其能夠提供足夠豐富的內部狀態x(n)，因此期望輸出ytarget(n)可由內部狀態x(n)的線性組合得出。

使ESN具有回聲狀態的重要條件是其內部權值矩陣W的譜半徑小于1。按照如下公式所得到內部權值矩陣，其網絡結構則具有回聲狀態特性，不論Win、Wback如何選取[6]。

(6)

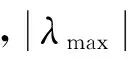
ESN與傳統神經網絡的重要區別是：ESN的Win、W和Wback是開始就確定好且固定不變的，模型只需訓練Wout，因此其具有訓練過程簡單的特點。

1.3 基于ESN的地區行業通用模型構建

該通用模型的基本思想為：選擇相同地區相同行業的若干只股票歷年數據作為訓練集并使用ESN進行訓練，本文建立上海地區房地產行業的通用模型，模型訓練好后就可以預測上海地區房地產行業內的任意股票。

1.4KMeans-ESN模型構建

基于KMeans-ESN模型的基本思想為：先用KMeans對訓練數據聚類，再對聚好的各類數據分別建立各自的ESN子模型，構成組合模型。訓練好后各子模型已經學習到聚類后的各類數據所具有的特征。預測時，先使用KMeans將訓練數據與待預測數據按照相同聚類指標一起聚類，然后根據待預測數據聚類后所屬的類別使用相應的ESN模型進行預測。模型整體流程如圖3所示。

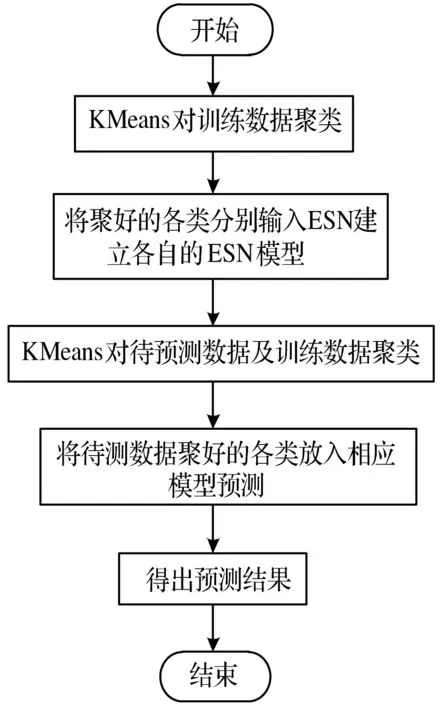
圖3 KMeans-ESN模型流程圖

2 仿真實驗

2.1 實驗假設及指標選取

由于前人所提出的股價預測方法都有一些假設條件，因此本文中使用模型對股價進行預測需遵循下述兩個假設[8]條件：

歷史會重演；股票價格反映一切信息。“歷史會重演”即表明股票價格會呈現一定的規律，過去的規律在未來會重現。“股票價格反映一切信息”即包括政治、經濟、心理、公司等所有影響股票價格的因素都會反映在股票價格中。

由于股價中的很多技術指標如移動均線、乖離率等都是基本指標開盤價、當日最高價、當日最低價、收盤價和成交量的初等變換，所以本文所有實驗只采用當日開盤價、當日最高價、當日最低價、當日收盤價和成交量這5個基本指標作為模型的輸入指標。

2.2 樣本數據選擇及處理

由于本文要建立地區行業通用模型，因此進行數據選擇時應選擇同一地區同一行業的股票數據。本文實驗選取了上證A股上海地區房地產行業10支股票2006年至2015年十年數據。

這十只股票分別為上海陸家嘴金融貿易區開發股份有限公司、上海華鑫股份有限公司、上海萬業企業股份有限公司、上海嘉寶實業(集團)股份有限公司、上海實業發展股份有限公司、上海世茂股份有限公司、上海新梅置業股份有限公司、上海市北高新股份有限公司、上海新黃浦置業股份有限公司、上海城投控股股份有限公司，所有數據均來自雅虎財經。

由于本文是對短期股票價格進行預測，且股票市場在每周都會進行調整，因此本文實驗以一周為周期，即用前四天即周一至周四4天的5個基本指標數據預測第五天即周五的收盤價。

首先對原始數據做預處理，將每只股票的數據按每5天分為一組，保證組內數據來自同一只股票。然后將原始數據歸一化到[-1,1]區間內。接下來構造輸入輸出學習模式，輸入數據為4天，包括當日開盤價、當日最高價、當日最低價、當日收盤價與成交量，維度為5維，總共為4天乘以5維等于20維。輸出數據為周五收盤價，所以為一維數據。按照前4天數據來預測后一天數據的學習模式，所有數據如此循環往復，構成一個個樣本。因此一個樣本的輸入為20維，輸出為一維。

為了使實驗結果有較強說服力，本文實驗借鑒10折交叉驗證的思想，即使用9只股票2006年至2010年數據做訓練，其余一只股票從2011年至2015年數據做測試，共做10次實驗，使每只股票都做一次測試。

2.3 聚類指標及模型評價指標選取

由于本文對股價的預測周期為一周，即5天，并且用周一至周四4天數據預測周五收盤價，因此本文所有聚類實驗均以5天即一周為單位，即將每只股票的數據按照每5天即一周分為一組。聚類時將相似的組聚為同一類。

因為一定時間段內數據的方差能夠反映該段時間內數據的波動程度，而收盤價是當日行情的標準，也是下一個交易日開盤價的依據，同時投資者對行情分析時一般采用收盤價作為計算依據，因此這里我們引入每組前4天即周一至周四收盤價方差、每組周一至周四當日最高價與最低價之差的均值兩個統計量[9]進行聚類。使用這兩個統計量作為聚類指標進行聚類是基于數據波動性的聚類。

本文模型評價指標采用具有代表性和普遍性的均方根誤差(RMSE)作為模型的評價指標。

2.4 基于ESN的上海地區房地產行業通用模型

由樣本輸入維數可知ESN輸入節點數為20，輸出節點數為1，設置儲備池內部節點數為100，儲備池稀疏度為10%，W譜半徑為0.8，輸入收縮因子為0.1。由于篇幅有限，本文只給出上海萬業企業股份有限公司做測試，其余9只做訓練時的訓練測試過程圖，誤差則以表格形式(表1)全部給出。如圖4、圖5所示。

圖4 上海萬業企業股份有限公司做測試、其余9只做訓練時的訓練過程圖

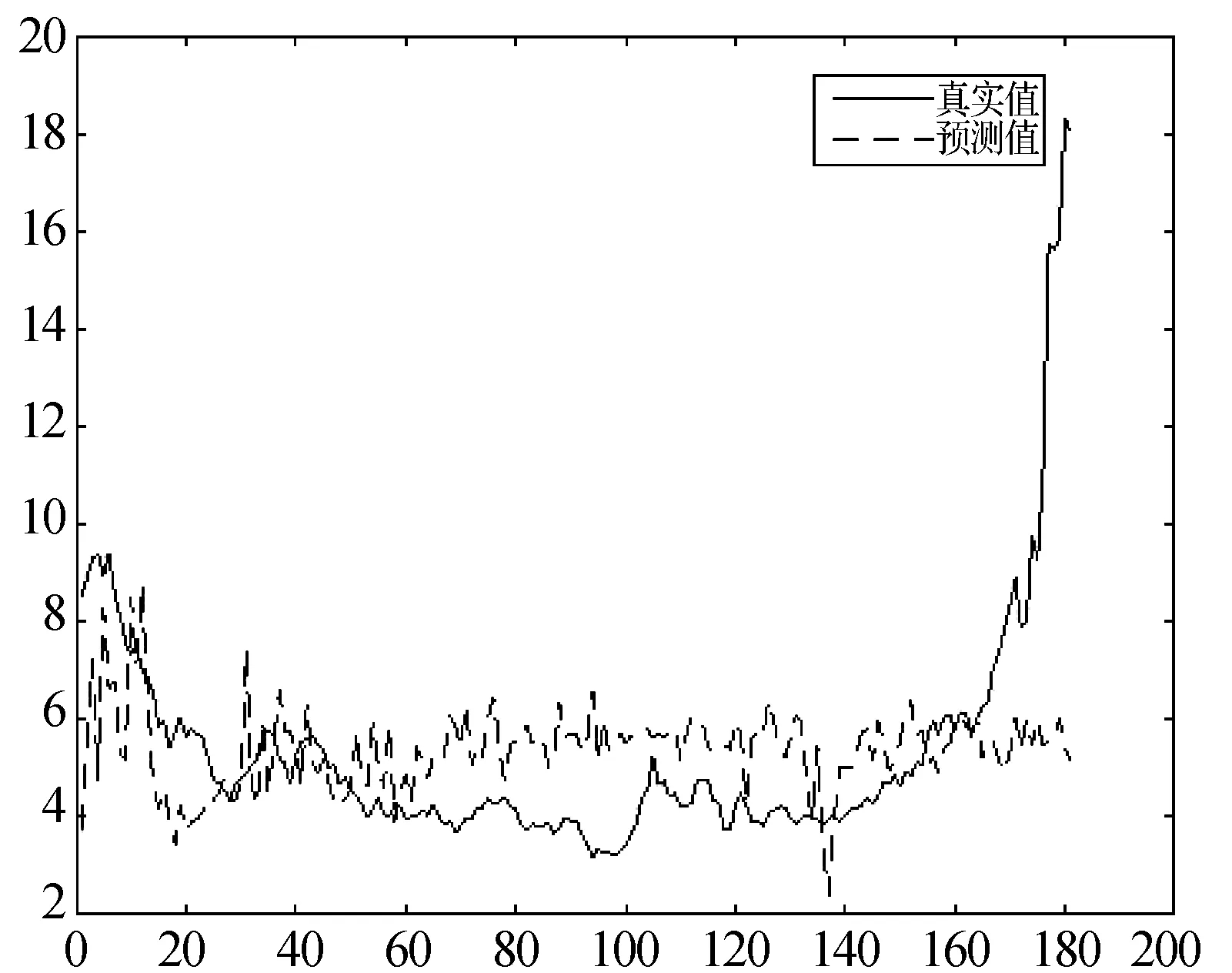
圖5 上海萬業企業股份有限公司做測試、其余9只做訓練時的測試過程圖

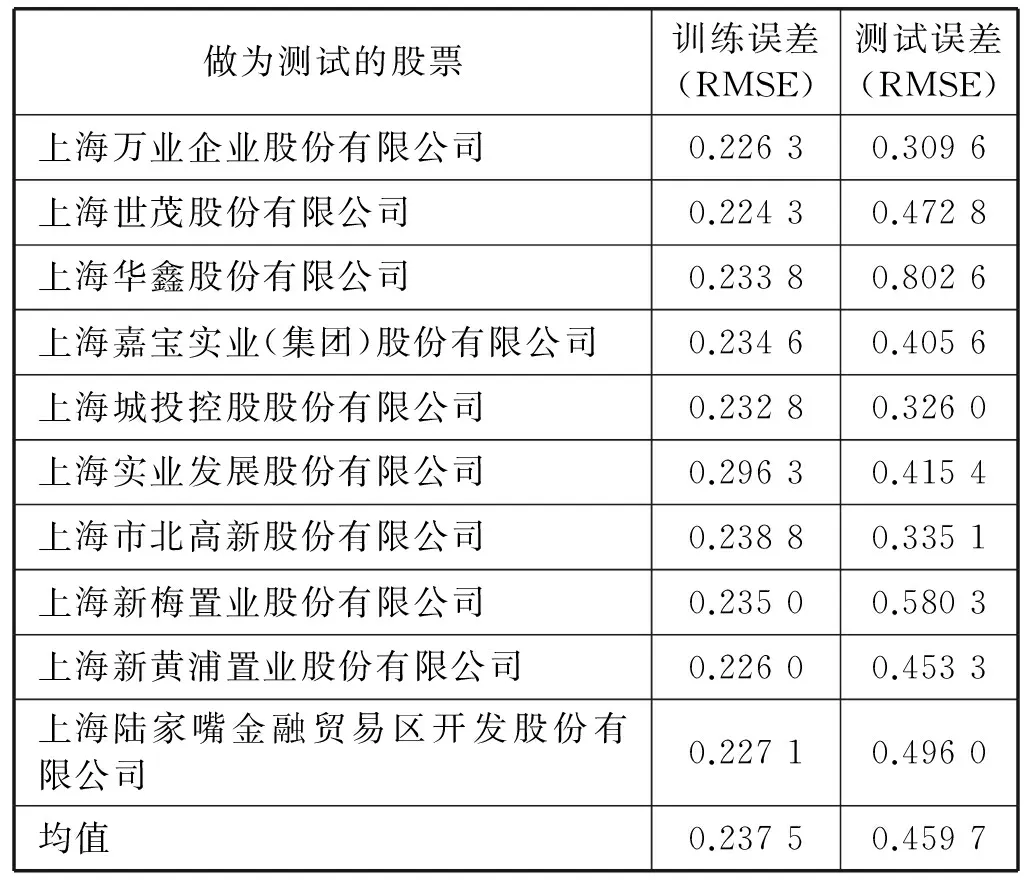
做為測試的股票訓練誤差(RMSE)測試誤差(RMSE)上海萬業企業股份有限公司0.22630.3096上海世茂股份有限公司0.22430.4728上海華鑫股份有限公司0.23380.8026上海嘉寶實業(集團)股份有限公司0.23460.4056上海城投控股股份有限公司0.23280.3260上海實業發展股份有限公司0.29630.4154上海市北高新股份有限公司0.23880.3351上海新梅置業股份有限公司0.23500.5803上海新黃浦置業股份有限公司0.22600.4533上海陸家嘴金融貿易區開發股份有限公司0.22710.4960均值0.23750.4597

同時，使用10只股票分別建立各自的單只股票單獨模型，并進行測試。建立單只股票單獨模型時，訓練集使用2006年至2010年五年數據，測試集采用2011年至2015年五年數據，其訓練誤差如表2所示。

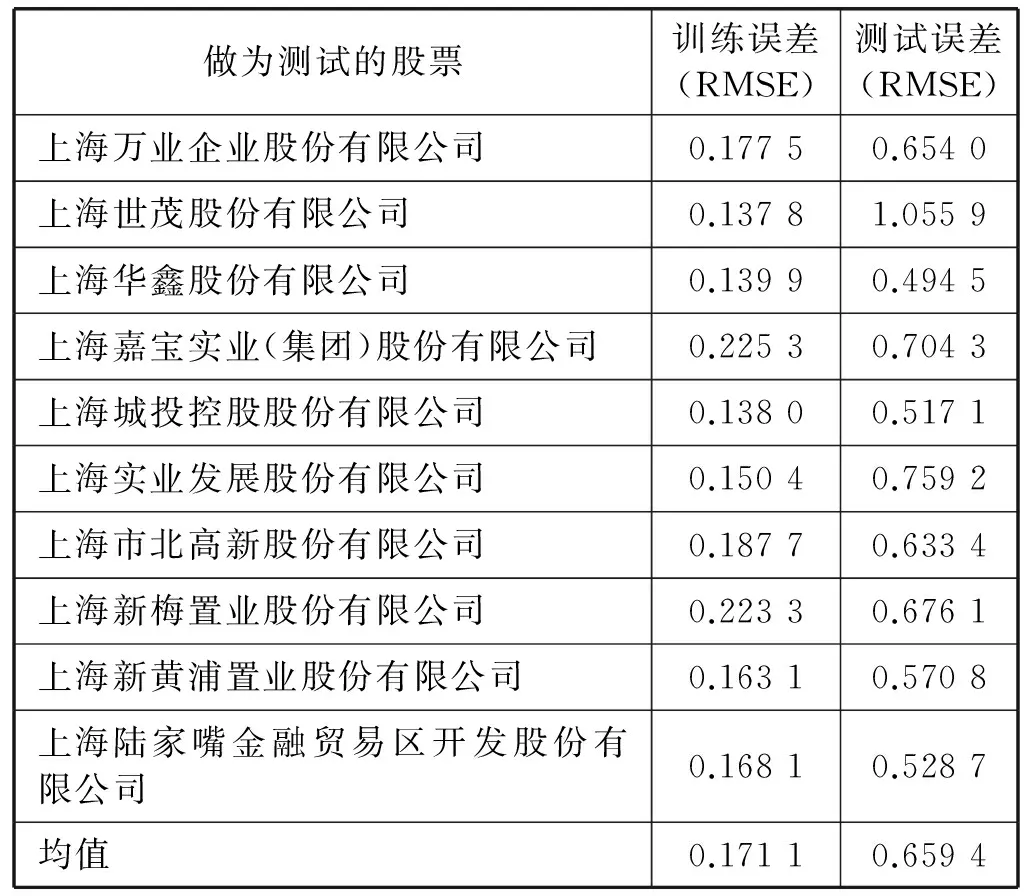
表2 ESN網絡各只股票單獨模型的訓練測試誤差

由表1及表2可以看出，上海地區房地產行業通用模型的預測精度要明顯高于單只股票模型。因為單只股票模型只包含了一只股票的相關信息，而影響單只股票價格的因素不僅有自身因素，還有同行業競爭者與互利共贏者等因素，而地區行業通用模型則相對全面地包含了這些相關信息，因此其模型預測效果更好。

2.5 基于波動性聚類的KMeans-ESN模型

按照基于波動性聚類，將數據聚為波動大、波動小兩類。本文給出上海陸家嘴金融貿易做測試，其余9只股票數據做訓練時的聚類圖，聚類結果如圖6所示。

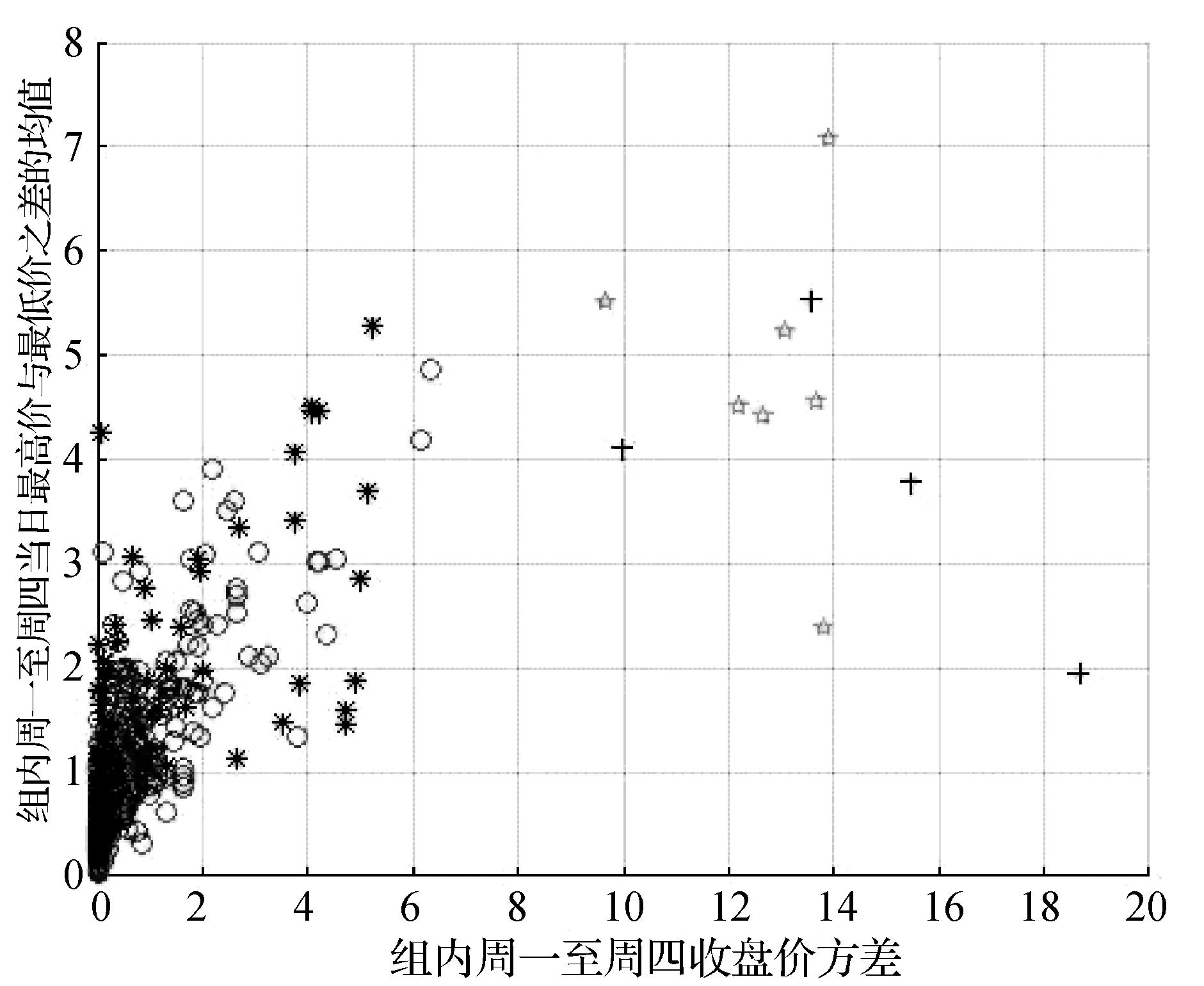
圖6 基于波動性聚類的訓練集與測試集數據聚類散點圖上海陸家嘴金融貿易做測試，其余9只股票數據做訓練

圖6中，圓圈和雪花型數據離原點較近，分別為訓練集和測試集波動小類數據，十字和星型離原點較遠，分別為訓練集和測試集波動大類數據。

聚類后將兩類數據分別建立相應的ESN模型，并做測試，兩類模型誤差分別如表3和表4所示。

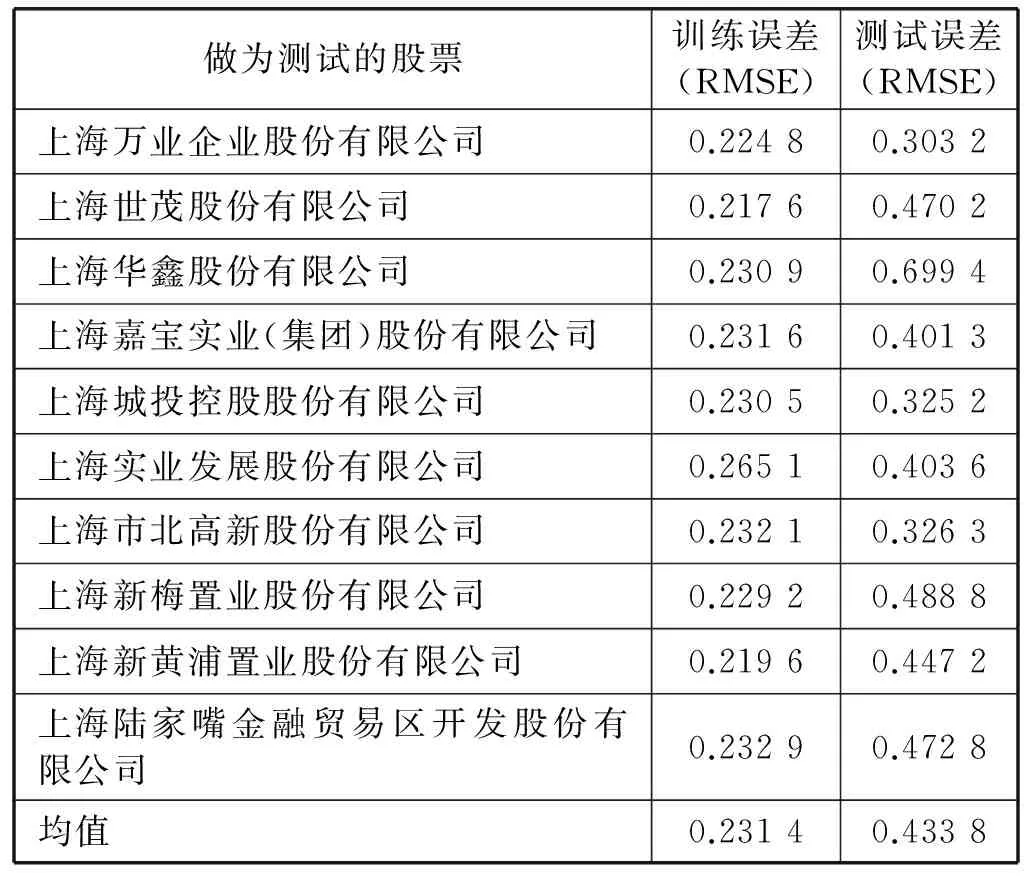
表3 波動小類ESN模型各只股票做測試時的訓練測試誤差

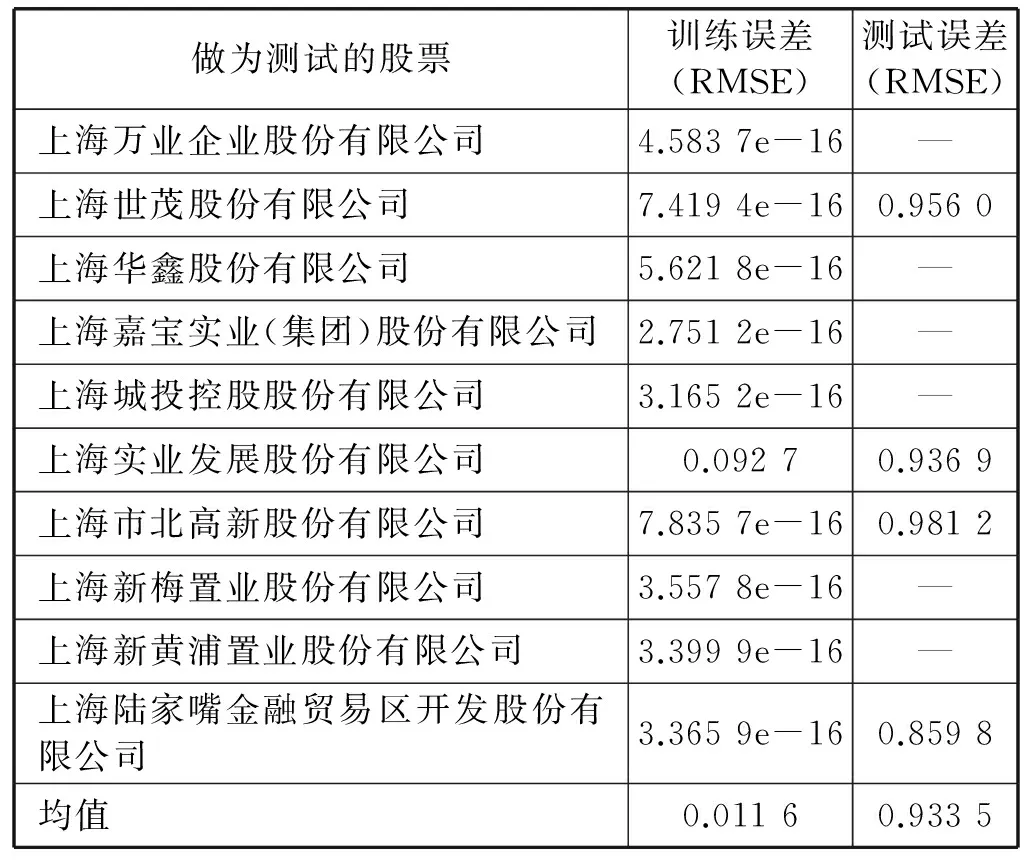
表4 波動大類ESN模型各只股票做測試時的訓練測試誤差

表4中的橫線表示對該只股票與其余9只訓練集股票做聚類時，該股票聚類結果為空。由表3和表4可以得出，波動小類的ESN模型預測效果要好于波動大類的ESN模型。

2.6 實驗結果及對比

本文ESN通用模型和基于數據波動性的聚類模型比較結果如表5所示。

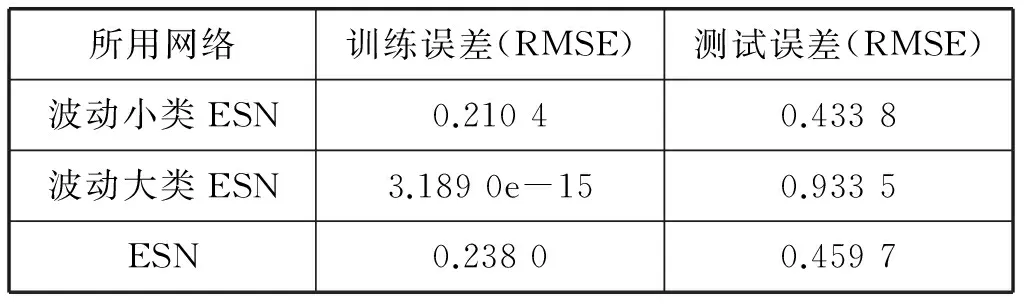
表5 各網絡訓練預測誤差比較

由表5可知，波動小的數據所訓練出的ESN模型預測效果最好，ESN模型次之，波動大的數據所訓練出的ESN模型最差。因此，波動小的數據適合使用基于數據波動性聚類的KMeans-ESN短期股價預測模型進行預測；波動大的數據適合使用基于ESN的短期股價預測通用模型進行預測。

3 結 語

本文使用ESN建立了上海地區房地產行業的短期股價預測通用模型，簡化了訓練過程，且與單只股票預測模型相比，該通用模型預測精度明顯提高。在此基礎上將KMeans聚類和回聲狀態網絡相結合，提出了一種新的時間序列股票預測模型。由實驗分析可知，基于ESN的短期股價預測模型適合波動大的數據、基于數據波動性聚類的KMeans-ESN短期股價預測模型適合波動小的數據。

對于模型的優化，嘗試使用不同聚類算法與回聲狀態網絡結合使用，并將其結果集成以及對回聲狀態網絡算法由監督到無監督學習的改進是今后的研究方向。

[1] 瓦伊尼 . 金融機構、金融工具和金融市場[M]. 陳未, 曾剛, 盧爽, 譯. 4版. 中國人民大學出版社, 2004.

[2] 林俊國.證券投資學[M].北京:經濟科學出版社,2006.

[3] 孫雪, 李昆侖, 胡夕坤, 等. 基于半監督K-means的K值全局尋優算法[J]. 北京交通大學學報, 2009, 33(6): 106-109.

[4]JaegerH.The“echostate”approachtoanalysingandtrainingrecurrentneuralnetworks[R].Berlin:GermanNationalResearchCenterforInformationTechnology, 2001.

[5] 韓敏. 基于儲備池的非線性系統預測理論與分析方法[M]. 大連:中國水利水電出版社, 2011.

[6]JaegerH.Tutorialontrainingrecurrentneuralnetworks,coveringBPTT,RTRL,EKFandthe"echostatenetwork"approach[R].Berlin:GermanNationalResearchCenterforInformationTechnology, 2013.

[7]LukosˇevicˇiusM.APracticalGuidetoApplyingEchoStateNetworks[M].Berlin:NeuralNetworks, 2012:659-686.

[8]ZahediJ,RounaghiMM.ApplicationofartificialneuralnetworkmodelsandprincipalcomponentanalysismethodinpredictingstockpricesonTehranStockExchange[J].PhysicaA, 2015, 438(438): 178-187.

[9] 何曉群. 現代統計分析方法與應用[M]. 中國人民大學出版社, 1998.

SHORT-TERM STOCK PRICE FORECAST MODEL BASED ON ECHO STATE NETWORK

Zhang Bin

(SchoolofInformationScienceandTechnology,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China)

Aiming at the problem that traditional single stock forecast model has low prediction precision and the complexity of traditional neural network training process, a general model of regional industry based on ESN is proposed. The model can predict the same industry in the same region in any stock. This paper uses ESN to set up the general model of stock price forecast in Shanghai real estate industry, simplifies the training process, and compared with the single stock forecasting model, the forecast accuracy of the general model is obviously improved. On the basis of general model, this paper proposes a KMeans-ESN model based on data volatility clustering. Experiments show that the short-term stock price forecasting model based on ESN is suitable for large-scale data, and the KMeans-ESN short-term stock price forecasting model based on data volatility clustering is suitable for small fluctuation data.

KMeans Echo state network Short-term stock price forecast General model Fluctuations

2016-05-11。張斌，碩士生，主研領域：數據挖掘。

TP399

A

10.3969/j.issn.1000-386x.2017.05.046