一種基于改進(jìn)的Logistic映射的數(shù)據(jù)不變長加密算法
楊鼎鼎 王 靜 陳世強
(湖北民族學(xué)院理學(xué)院 湖北 恩施 445000)
一種基于改進(jìn)的Logistic映射的數(shù)據(jù)不變長加密算法
楊鼎鼎 王 靜 陳世強*
(湖北民族學(xué)院理學(xué)院 湖北 恩施 445000)
針對數(shù)據(jù)不變長加密,提出一種基于改進(jìn)的Logistic映射的加密算法。利用該映射產(chǎn)生的混沌序列所特有的不可預(yù)測性,對序列X進(jìn)行不變長加密。即明文X的Bit長度為n,用該算法對X進(jìn)行加密運算后得到的密文Y的Bit長度還是n。實驗結(jié)果表明,該算法效率高,內(nèi)存消耗少,抗攻擊性強,且普遍適用于不改變數(shù)據(jù)長度需求的加解密應(yīng)用。
不變長加密Logistic映射 對稱加密 混沌序列
0 引 言
隨著信息化的迅速發(fā)展,各種網(wǎng)絡(luò)攻擊使信息的安全傳輸越來越得不到保障,針對這些不安全因素,人們提出了許多數(shù)據(jù)加密算法[1-3]。數(shù)據(jù)加密方法普遍會增加密文數(shù)據(jù)的長度,給信息的傳輸和存儲增加額外的負(fù)擔(dān)。針對這個問題,人們開始關(guān)注數(shù)據(jù)加密后密文數(shù)據(jù)長度不變的算法,目前對不變長加密的研究已成為數(shù)據(jù)加密的一個熱點。
數(shù)據(jù)加密自20世界70年代提出以來,影響深遠(yuǎn)的對稱加密算法主要有3種:DES、3DES、AES。DES加密算法[4-9]為密碼體制中的對稱密碼體制,又被稱為數(shù)據(jù)加密標(biāo)準(zhǔn),是1972年美國IBM公司研制的對稱密碼體制加密算法,是一種變長的數(shù)據(jù)加密算法。文獻(xiàn)[4-5]介紹了DES加密算法的理論知識及實現(xiàn)過程;文獻(xiàn)[6]研究了DES算法的抗攻擊性,得出其分組、密鑰、密碼生命周期都比較短,DES加密的數(shù)據(jù)容易被破解;文獻(xiàn)[7]指出通過窮舉搜索法也能破解DES加密的數(shù)據(jù);基于C++平臺下實現(xiàn)DES算法[8],研究了DES算法機理并在C++的平臺下予以實現(xiàn)。針對DES的可破解性,人們提出了3DES加密算法。3DES(或稱為Triple DES)是三重數(shù)據(jù)加密算法TDEA(Triple Data Encryption Algorithm)塊密碼的通稱,也是DES向AES過渡的加密算法。文獻(xiàn)[10]對DES和3DES分組加密算法模型進(jìn)行了分析,指出通過窮舉攻擊、差分攻擊和線性攻擊可以破解DES算法加密的數(shù)據(jù)。3DES算法對DES算法作了改進(jìn),使用三個密鑰對DES進(jìn)行了三重調(diào)用,增加了密文的抗攻擊性,但也增加了加密和解密的復(fù)雜度。AES(Advanced Encryption Standard)高級加密標(biāo)準(zhǔn)[11-14],又稱Rijndael加密法,是美國政府采用的一種區(qū)塊加密標(biāo)準(zhǔn),是一種不變長加密算法。文獻(xiàn)[11]對AES算法進(jìn)行了分析并進(jìn)行了C++實驗,實驗證明AES具有更好的安全性。文獻(xiàn)[12]分析了AES算法的抗攻擊性,并給出了該算法在信息安全中的一些應(yīng)用。文獻(xiàn)[13]應(yīng)用NVIDIA的CUDA語言對隨機數(shù)據(jù)分別實現(xiàn)DES和AES加密,發(fā)現(xiàn)使用CUDA語言更加節(jié)約時間和內(nèi)存;文獻(xiàn)[14]探索實現(xiàn)AES快速加密的軟件,提出了第一個實施AES解密的GPU架構(gòu)。加密算法從DES發(fā)展到AES,引發(fā)了數(shù)據(jù)加密從變長到不變長的發(fā)展趨勢。
繼AES加密算法之后,一些有效的數(shù)據(jù)加密算法相繼被提出。文獻(xiàn)[15]研究了Logistic映射的時間序列、功率譜所表現(xiàn)出來的特性,說明了對費根鮑姆(Feigenbaum)常數(shù)研究的意義;文獻(xiàn)[16]提出一種混沌加密算法,利用正切函數(shù)和冪函數(shù)設(shè)計混沌迭代函數(shù),算法具有很好的發(fā)散性,但加、解密運算速度慢;基于數(shù)字化混沌密碼系統(tǒng)的改進(jìn)算法[17],通過m序列隨機改變混沌映射的參數(shù),克服了混沌序列的有限狀態(tài),但子空間轉(zhuǎn)換存在時間延遲,影響加密效率,且難以體現(xiàn)混沌迭代的隨機性;文獻(xiàn)[18]利用混沌系統(tǒng)對初始條件的敏感性及混沌軌道的非周期性,通過增加密鑰參數(shù)數(shù)量,增強了加密數(shù)據(jù)的安全性,但也增加了加密、解密難度;基于約瑟夫環(huán)的數(shù)據(jù)不變長加密[19],算法實現(xiàn)簡單,運算速率快,但安全性較低,容易被破解;基于改進(jìn)的Logistic混沌映射的數(shù)字圖像加密[20],能夠抵抗明文統(tǒng)計的攻擊,密鑰空間大,但算法復(fù)雜;文獻(xiàn)[21]通過增加放大因子,獲得更加隨機的混沌序列,但增加了映射的復(fù)雜度;基于量子Logistic映射的小波域圖像加密[22],加密算法敏感性強、安全性高,但效率低。
針對目前數(shù)據(jù)不變長加密存在的不足,提出了一種基于改進(jìn)的Logistic映射的數(shù)據(jù)不變長加密算法,該算法運行時間短、效率高。實驗結(jié)果表明,該算法抗攻擊性強,安全性高。
1 Logistic映射及其改進(jìn)
1.1Logistic映射
Logistic映射是一個非線性迭代方程,雖然具有確定的形式,但卻能產(chǎn)生完全隨機的、對混沌系數(shù)μ的動態(tài)變化和初值極x0為敏感的混沌序列。利用混沌序列進(jìn)行數(shù)據(jù)加密具有非常強的抗破譯能力。Logistic映射的一般形式為:
xn+1=μ×xn×(1-xn)
(1)
式中,xn為映射變量,0≤xn≤1;μ為系統(tǒng)參數(shù),0≤μ≤4。當(dāng)3.569 945 673≤μ≤4時,該映射處于混沌狀態(tài),產(chǎn)生實值混沌序列。若選定μ=3.7的Logistic映射產(chǎn)生混沌序列,即xn+1=3.7xn×(1-xn),xn∈(0,1),該映射對不同初始值進(jìn)行迭代后的結(jié)果如圖1所示。

圖1 Logistic混沌序列
根據(jù)圖1,該映射對初始值非常敏感,產(chǎn)生的序列隨機性強,且輸出均分布在(0,1)內(nèi)。
1.2 改進(jìn)的Logistic映射
μ落在區(qū)間3.569 945 673……<μ<4內(nèi)時,Logistic映射產(chǎn)生的序列處于混沌狀態(tài),且μ取值為4時,混沌迭代方程xn+1=4×xn×(1-xn)能產(chǎn)生最佳混沌效果,但加密失去一定的安全性。為使加密數(shù)據(jù)更加安全,可將式(1)中的混沌系數(shù)μ用一個值域上限接近4的表達(dá)式代替,利用參數(shù)不停的無周期地變化性,增加數(shù)據(jù)的安全性。基于上述思想,將logistic映射改為以下模型:
xn+1= [μ0+(4-μ0)×cos((10-6+xn)×π/2)]×
xn×(1-xn/n)
(2)
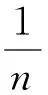
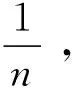
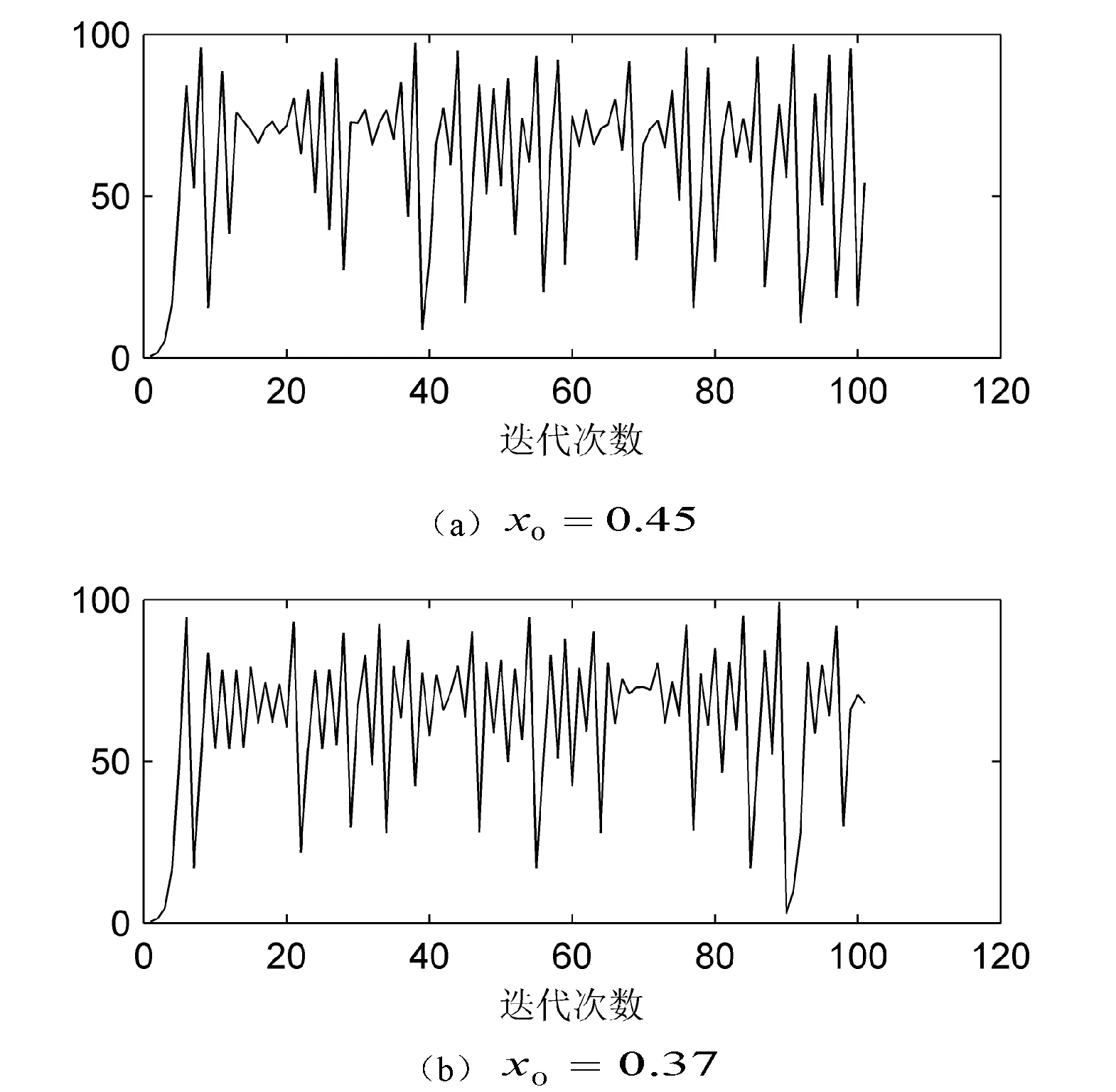
圖2 改進(jìn)的Logistic混沌序列
1.3 安全性分析
對比圖1和圖2,改進(jìn)的Logistic映射放大了原Logistic映射的結(jié)果范圍。假設(shè)明文數(shù)據(jù)流中每個字節(jié)的十進(jìn)制值為k,原Logistic映射加密后其值落在[0,k]之間,改進(jìn)的Logistic映射加密后其值落在[0,100k]之間,數(shù)值映射范圍擴大了100倍。根據(jù)圖2,若隨機給定迭代次數(shù)n,可得到具有高隨機性的密鑰Key(n),用這些秘鑰加密明文可得到更不可預(yù)測的密文序列,安全性更高。
2 數(shù)據(jù)加密與解密
2.1 數(shù)據(jù)加密
2.1.1 加密算法描述
給定一個十進(jìn)制序列X=(x1,x2,…,xn),數(shù)據(jù)加密算法描述如下:
(1) 將十進(jìn)制序列X轉(zhuǎn)化為n×1階二進(jìn)制串組成的矩陣,并將n×1階矩陣轉(zhuǎn)化為n×m階矩陣X′。X′=(x11,x12,…,x1m;x21,x22,…,x2m;xn1,xn2,…,xnm),其中X′的每個元素xij(i=1,2,…,n;j=1,2,…,m)由0、1二進(jìn)制串組成(0、1的個數(shù)由加密算法中的參數(shù)n決定)。若X由n個十進(jìn)制數(shù)組成,則X′由n×m個二進(jìn)制數(shù)組成,轉(zhuǎn)化的空間復(fù)雜度為S(n)。
(2) 應(yīng)用Logistic映射對(1)中n×m階矩陣X′的每個元素進(jìn)行加密,得到加密后的n×m階矩陣Y′。
設(shè)Y′=(y11,y12,…,y1m;y21,y22,…,y2m;yn1,yn2,…,ynm),yij∈{0,1},(i=1,2,…,n;j=1,2,…,m),Y′與X′大小相同,都是n×m階矩陣。
(3) 將(2)中的n×m階矩陣Y′轉(zhuǎn)化為n×1階二進(jìn)制串組成的矩陣,再轉(zhuǎn)化為十進(jìn)制密文序列Y=(y1,y2,…,yn)。
其中,密文序列Y與明文序列X長度一樣,都是n。
2.1.2 加密算法實現(xiàn)
Step1 輸入?yún)?shù)
明文數(shù)據(jù)X,密鑰(n,m,nb)
n:十進(jìn)制數(shù)用n個二進(jìn)制數(shù)表示
m:用戶自定義的隨機數(shù)
nb:其他進(jìn)制數(shù)轉(zhuǎn)十進(jìn)制的基數(shù)
Step2 加密數(shù)據(jù)
(1) 開始計時;
(2) 計算X的長度lX并將其轉(zhuǎn)化為二進(jìn)制數(shù);
(3) 遍歷所有的二進(jìn)制數(shù),將二進(jìn)制數(shù)轉(zhuǎn)化為對應(yīng)矩陣;
(4) 遍歷矩陣中所有的數(shù),用改進(jìn)的Logistic映射對矩陣中每個數(shù)據(jù)進(jìn)行加密;
(5) 得到加密數(shù)據(jù)并將其轉(zhuǎn)化為十進(jìn)制數(shù);
(6) 計時結(jié)束,查看內(nèi)存使用情況。
2.2 數(shù)據(jù)解密
2.2.1 解密算法描述
若序列Y=(y1,y2,…,yn)為經(jīng)過加密變換后得到的序列,則其解密算法描述如下:
(1) 將十進(jìn)制序列Y轉(zhuǎn)化為n×1階二進(jìn)制串組成的矩陣,并將n×1階矩陣轉(zhuǎn)化n×m階矩陣Y′。Y′=(y11,y12,…,y1m;y21,y22,…,y2m;yn1,yn2,…,ynm),其中Y′的每個元素yij(i=1,2,…,n;j=1,2,…,m)由0、1二進(jìn)制串組成(0、1的個數(shù)由解密算法中的參數(shù)n決定)。若Y由n個十進(jìn)制數(shù)組成,則Y′由n×m個二進(jìn)制數(shù)組成,轉(zhuǎn)化的空間復(fù)雜度為S(n)。
(2) 應(yīng)用Logistic逆映射對(1)中n×m階矩陣Y′的每個元素進(jìn)行解密,得到解密后的n×m階矩陣X′。
設(shè)X′=(x11,x12,…,x1m;x21,x22,…,x2m;xn1,xn2,…,xnm),xij∈{0,1},(i=1,2,…,n;j=1,2,…,m),X′與Y′大小相同,都是n×m階矩陣。
(3) 將(2)中的n×m階矩陣X′轉(zhuǎn)化為n×1階二進(jìn)制串組成的矩陣,再轉(zhuǎn)化為十進(jìn)制明文序列X=(x1,x2,…,xn)。
其中,密文序列Y的長度與明文序列的X長度一樣,都是n。
2.2.2 解密算法實現(xiàn)
Step1 輸入?yún)?shù)
密文數(shù)據(jù)Y,密鑰(n,m,nb)
Step2 解密數(shù)據(jù)
(1) 開始計時;
(2) 計算Y的長度lY并將其轉(zhuǎn)化為二進(jìn)制數(shù);
(3) 遍歷所有的二進(jìn)制數(shù),將二進(jìn)制數(shù)轉(zhuǎn)化為對應(yīng)矩陣;
(4) 遍歷矩陣中所有的數(shù),對矩陣中每個數(shù)用改進(jìn)的Logistic逆映射進(jìn)行解密;
(5) 得到解密后的數(shù)據(jù)并將其轉(zhuǎn)化為十進(jìn)制數(shù);
(6) 計時結(jié)束,查看內(nèi)存使用情況。
3 實驗結(jié)果及分析
3.1 實驗平臺
PC機配置為:Intel(R)Core(TM)i5-4200MCPU@ 2.5GHz2.5GHz,內(nèi)存4GB,win7 32位操作系統(tǒng)。通過MATLAB2014a編寫程序?qū)崿F(xiàn)上述加解密算法。
3.2 實驗結(jié)果與分析
選取50組介于0~255的數(shù)據(jù)進(jìn)行實驗,每組數(shù)據(jù)含16個元素。改進(jìn)的Logistic模型中xn和n都是變量,不需要賦初值。
3.2.1 抗攻擊性分析
(1) 信息熵
根據(jù)香農(nóng)定理[23],熵是用來描述信息的不確定性,反映含有信息多少的信息量。數(shù)據(jù)越混亂,所含的信息就越少,信息熵就越大。數(shù)據(jù)的信息熵的計算公式為:
(3)
式中,P(mi)為數(shù)據(jù)mi的概率;n為數(shù)據(jù)的個數(shù)。表1顯示了約瑟夫環(huán)算法、AES算法、Logistic算法和改進(jìn)的Logistic算法的信息熵差異,改進(jìn)的Logistic算法的信息熵達(dá)到百萬級,其他三種算法的信息熵都在1 000以內(nèi),改進(jìn)的Logistic算法的抗攻擊性更好。

表1 信息熵比較
(2) 數(shù)據(jù)相關(guān)性
實驗對加密數(shù)據(jù)與原始數(shù)據(jù)進(jìn)行了相關(guān)性分析。若加密數(shù)據(jù)與原始數(shù)據(jù)的相關(guān)性越大,加密效果越差;反之,加密效果越好。相關(guān)系數(shù)的計算公式如式(4)所示[24]:
(4)
式中,x、y表示原始數(shù)據(jù)與加密數(shù)據(jù);K表示數(shù)據(jù)的字節(jié)個數(shù);E(x)表示x的數(shù)學(xué)期望;D(x)表示x的方差;cov(x,y)代表x、y的協(xié)方差;rxy表示x、y的相關(guān)系數(shù)。表2比較了四種算法的數(shù)據(jù)相關(guān)性計算結(jié)果,AES的數(shù)據(jù)相關(guān)性最低,改進(jìn)的Logistic映射與約瑟夫環(huán)接近且顯著低于原Logistic算法,改進(jìn)的Logistic算法的抗攻擊性明顯提高。

表2 數(shù)據(jù)相關(guān)最小相關(guān)比較
3.2.2 密鑰空間
根據(jù)Kerckhoff準(zhǔn)則[25],一個好的加密算法應(yīng)該具備足夠大的密鑰空間。改進(jìn)的Logistic算法的n、m(可無窮大)、nb都是十進(jìn)制小數(shù),假設(shè)計算機精度為10-15,那么密鑰空間為3×1045>1045。四種算法的密鑰空間比較見表3所示,改進(jìn)的Logistic算法的密鑰空間最大,比約瑟夫環(huán)算法大約1015倍,可更好抗擊窮舉法的攻擊。

表3 密鑰空間比較
3.2.3 算法復(fù)雜度
改進(jìn)的Logistic算法使用簡單運算,使每個加密數(shù)據(jù)在隨機算法中迭代1次,保證算法安全的基礎(chǔ)上盡可能減少了加密計算量。在上述搭建的平臺下,分別對四種加密算法進(jìn)行實驗。每次實驗分別對四種算法連續(xù)采樣50次,得到四組實驗樣本。表4為四種算法的計算復(fù)雜度對比。加密同樣的數(shù)據(jù),四種算法的加密時間有較大的差異,根據(jù)統(tǒng)計平均值來分析,改進(jìn)的Logistic算法加密時間最短,需要21ms;根據(jù)標(biāo)準(zhǔn)差分析,改進(jìn)的Logistic算法波動最小;改進(jìn)的Logistic算法相對Logistic算法、約瑟夫環(huán)算法和AES算法復(fù)雜度分別下降67.2%、62.5%和96.8%,因此改進(jìn)的Logistic算法計算復(fù)雜度最低。圖3為四種算法的加密時間比較,改進(jìn)的Logistic算法的時間曲線比其他三種加密算法都低,所用時間最少,計算復(fù)雜度低,更適合實時保密系統(tǒng)。
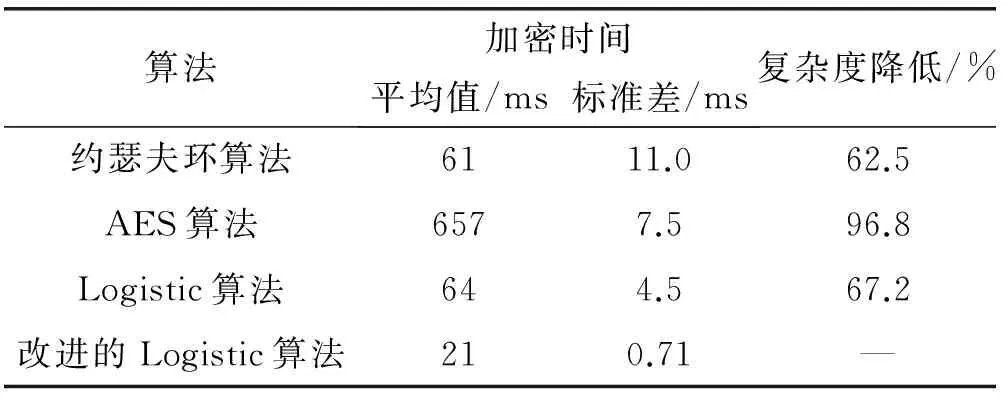
表4 計算復(fù)雜度對比
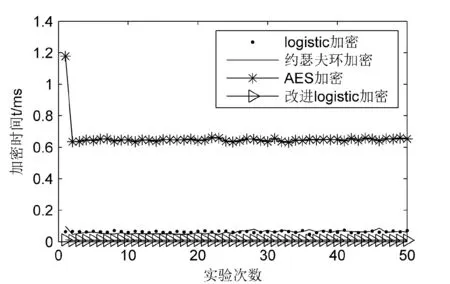
圖3 加密時間對比
改進(jìn)的Logistic算法對全部數(shù)據(jù)主要進(jìn)行3次大數(shù)量級運算,保證算法安全的基礎(chǔ)上盡可能減少了計算機的內(nèi)存消耗。在上述搭建的平臺下,分別對四種加密算法進(jìn)行實驗。每次實驗分別對四種算法連續(xù)采樣50次,得到4組實驗樣本。表5為四種算法的內(nèi)存消耗對比。加密同樣的數(shù)據(jù),四種算法的內(nèi)存消耗有較大的差異,根據(jù)平均值分析,改進(jìn)的Logistic算法內(nèi)存消耗最少,消耗內(nèi)存519 306 772KB;根據(jù)標(biāo)準(zhǔn)差分析,Logistic算法內(nèi)存消耗恒定,改進(jìn)的Logistic算法開始存在潑動,漸漸趨于恒定;改進(jìn)的Logistic算法相對Logistic算法、約瑟夫環(huán)算法和AES算法內(nèi)存消耗分別下降21%、24%和31.7%,故改進(jìn)的Logistic算法內(nèi)存消耗最少。圖4為四種算法的內(nèi)存消耗比較,改進(jìn)的Logistic算法的時間曲線比其他三種加密算法都低,消耗內(nèi)存最少。
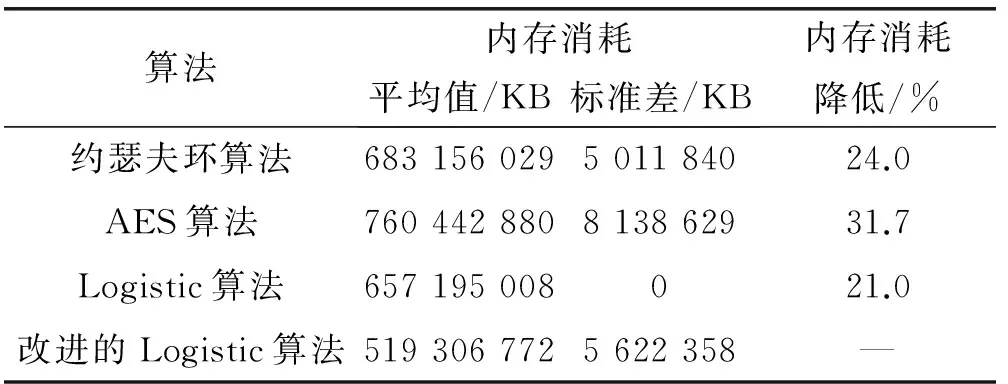
表5 內(nèi)存消耗對比
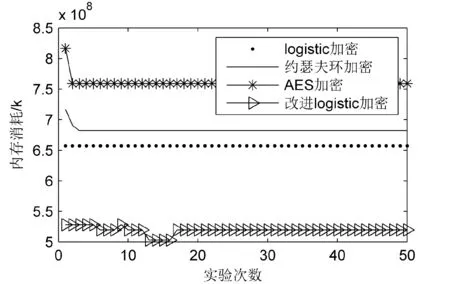
圖4 內(nèi)存消耗對比
3.2.4 加密敏感性
敏感性分析主要考察對密鑰和明文的敏感性,其操作方法是對明文或密鑰中做微小的改變,計算通過加密算法得到的對應(yīng)密文的變化率CRC(Thechangerateofciphertext),其計算公式為:
(5)
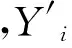
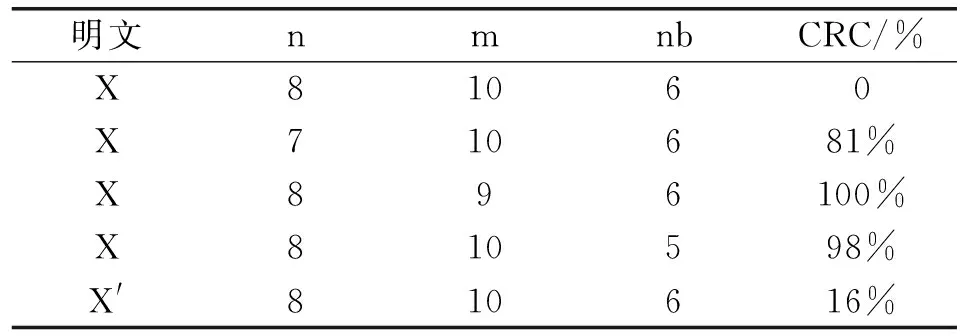
表6 改進(jìn)logistic算法對密鑰敏感性測試
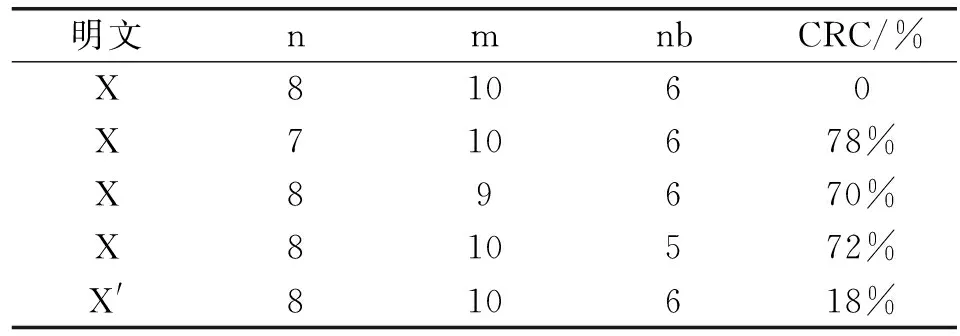
表7 約瑟夫環(huán)算法對密鑰敏感性測試
4 結(jié) 語
針對數(shù)據(jù)加密時間長、內(nèi)存消耗大和加密后長度改變的問題,提出一種基于改進(jìn)的Logistic映射的數(shù)據(jù)不變長加密算法。該算法進(jìn)行數(shù)據(jù)加密,不僅加密所需時間短、內(nèi)存消耗小,而且可以保證加密后的數(shù)據(jù)與原數(shù)據(jù)長度相同,抗攻擊性能突出。
[1] Masui M,Ishii H,Anan T,et al.Document data encryption method and document data encryption system: EP2157560[P/OL].2009-06-08.[2010-02-24].http://xueshu.baidu.com/s?wd=paperuri%3A%28d746826a6b6fa22be46f1758 c47a45d1%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.freepatentsonline.com%2FEP2157560.html&ie=utf-8.
[2] Kirichenko A.Data encryption:7319751[P/OL].2002-10-11.[2008-01-15].http://xueshu.baidu.com/s?wd=paperuri%3A%28e5106cf7be864c61b21489baec7837fa%29& filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.freepatentsonline.com%2F7319751.html&ie=utf-8.
[3] Diffie W,Hellman M E.New directions in cryptography[J].IEEE Transactions on Information Theory,1976,22(6):644-654.
[4] Biryukov A,Cannière C D.Data encryption standard (DES)[M]//Encyclopedia of Cryptography and Security.New York,NY,USA:Springer US,2005:129-135.
[5] US Department of Commerce.Data encryption standard (DES):FIPS PUB 46-2[S].USA:National Institute of Standards and Technology,1999.
[6] 王立勝,王磊,顧訓(xùn)穰.數(shù)據(jù)加密標(biāo)準(zhǔn)DES分析及其攻擊研究[J].計算機工程,2003,29(13):130-132.
[7] 靳冰,賴宏慧,賈玉珍.DES加密算法的安全分析[J].華南金融電腦,2007,15(2):71-73.
[8] 狄冬豐.基于C++平臺下實現(xiàn)DES算法[J].長沙通信職業(yè)技術(shù)學(xué)院學(xué)報,2013,12(2):35-38.
[9] Saputra H,Vijaykrishnan N,Kandemir M,et al.Masking the energy behavior of DES encryption[smart cards][C]//Design,Automation and Test in Europe Conference and Exhibition,2003:84-89.
[10] Zhang Y.Analysis of 3DES encryption algorithm[J].Computer & Digital Engineering,2014,42(8):1468-1471.
[11] 吳小博.AES加密算法分析與C++編程實現(xiàn)[J].計算機安全,2007(12):44-46.
[12] 張金輝,郭曉彪,符鑫.AES加密算法分析及其在信息安全中的應(yīng)用[J].信息網(wǎng)絡(luò)安全,2011(5):31-33.
[13] Luken B P,Ouyang M,Desoky A H.AES and DES encryption with GPU[C]//22nd International Conference on Parallel and Distributed Computing and Communication Systems,2009:67-70.
[14] Osvik D A,Bos J W,Stefan D,et al.Fast software encryption[C]//17th International Workshop on Fast Software Encryption.Springer,2010:75-93.
[15] 施偉鋒.Logistic映射及其混沌特性研究[J].光電技術(shù)應(yīng)用,2004,19(2):53-56.
[16] 高昊江,張宜生,梁書云,等.一種新的混沌加密算法及其應(yīng)用[J].小型微型計算機系統(tǒng),2006,27(4):655-657.
[17] 管春陽,高飛.一種基于混沌序列的加密算法[J].北京理工大學(xué)學(xué)報,2003,23(3):363-366.
[18] Frey D R.Chaotic digital encoding: an approach to secure communication[J].IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing,1993,40(10):660-666.
[19] 林清波,曾炳生.一種高效的數(shù)據(jù)不變長加密算法及其實現(xiàn)[J].福建農(nóng)林大學(xué)學(xué)報(自然科學(xué)版),2005,34(4):540-544.
[20] 徐兵,袁立.基于改進(jìn)Logistic混沌映射的數(shù)字圖像加密算法研究[J].計算機測量與控制,2014,22(7):2157-2159.
[21] 韓春艷,禹思敏.改進(jìn)的Logistic映射及其動力學(xué)特性[J].中國海洋大學(xué)學(xué)報,2015,45(5):120-125.
[22] 羅玉玲,杜明輝.基于量子Logistic映射的小波域圖像加密算法[J].華南理工大學(xué)學(xué)報(自然科學(xué)版),2013,41(6):53-62.
[23] Shannon C E.Communication theory of secrecy systems[J].The Bell System Technical Journal,1949,28(4):656-715.
[24] 郭毅,邵利平,楊璐.基于約瑟夫和Henon映射的比特位圖像加密算法[J].計算機應(yīng)用研究,2015,32(4):1131-1137.
[25] Kerckhoffs A.La cryptographie militaire[J].Journal des Sciences Militaires,1883,9:5-83.
AN ENCRYPTION ALGORITHM KEEPING DATA LENGTH UNCHANGED BASED ON MODIFIED LOGISTIC MAP
Yang Dingding Wang Jing Chen Shiqiang*
(SchoolofScience,HubeiUniversityforNationalities,Enshi445000,Hubei,China)
An encryption algorithm keeping data length unchanged based on modified Logistic map is proposed for encryption with length unchanged. By using the unpredictability of the chaotic sequence generated by this mapping, the sequenceXisencryptedwithdatalengthunchanged.ThebitlengthofplaintextXisn,andthebitlengthofciphertextYobtainedafterthealgorithmisusedtoencryptXisn.Experimentalresultsshowthatthealgorithmisefficient,lessmemoryconsumption,stronganti-attack,andisgenerallyapplicabletotheencryptionanddecryptionapplicationswithoutchangingthedatalengthrequirements.
Encryption with length unchanged Logistic map Symmetric encryption Chaotic sequence
2016-03-29。國家民委科研項目(14HBZ014);國家科技支撐計劃課題(2015BAK27B03)。楊鼎鼎,碩士生,主研領(lǐng)域:混沌密碼學(xué)及圖像處理。王靜,碩士生。陳世強,教授。
TP
ADOI:10.3969/j.issn.1000-386x.2017.05.051

