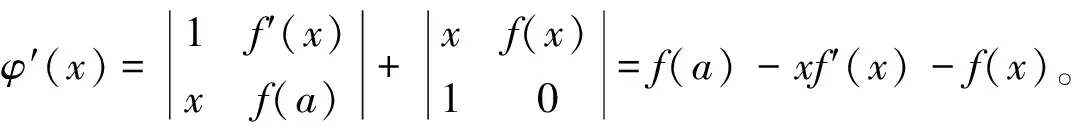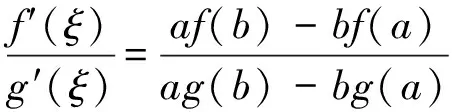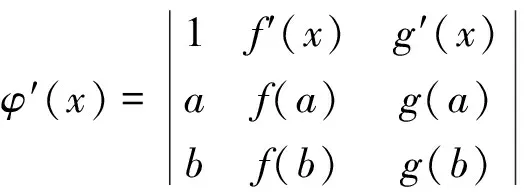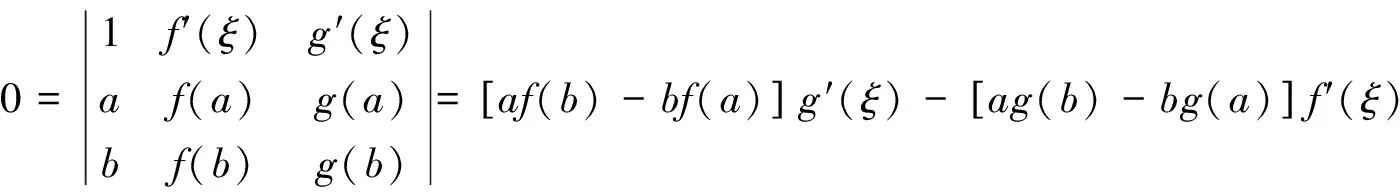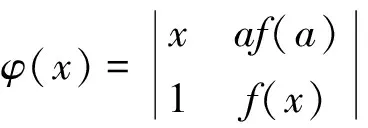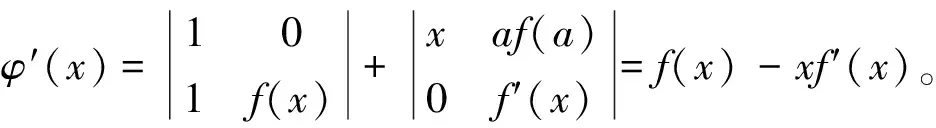中值定理的行列式法證明及推廣
王文華,陳崢立,李 瑋
(1.陜西師范大學 a.民族教育學院;b.數學與信息科學學院,西安 710062;2.武警工程大學 理學院,西安 710078)
【自然科學基礎理論研究】
中值定理的行列式法證明及推廣
王文華1a,陳崢立1b,李 瑋2
(1.陜西師范大學 a.民族教育學院;b.數學與信息科學學院,西安 710062;2.武警工程大學 理學院,西安 710078)
首先根據羅爾中值定理,構造行列式證明拉格朗日中值定理和柯西中值定理;其次,分別建立了3個函數和4個函數的中值定理以及二階可導函數的廣義中值定理;最后,列舉了通過構造行列式解決具體問題的實例。
行列式;導數;中值定理
0 引言
微分中值定理是微積分學中的一組重要定理,包括羅爾中值定理、拉格朗日中值定理和柯西中值定理,在微積分教學與研究中具有承前啟后的作用。然而,在證明了羅爾中值定理之后,如何再去證明拉格朗日中值定理和柯西中值定理,是一個比較困難的問題。通常采用的方法是構造輔助函數法,并且與微分中值定理相關的證明題,大多數也需要作輔助函數才能完成,因而構造輔助函數是證明此類問題的關鍵。目前的參考書上介紹了多種構造輔助函數的方法[1-3],但對于學生來講,要構造合適的輔助函數仍是比較困難的。目前已有不少關于如何構造輔助函數的討論與研究,例如:文獻[4]給出了用原函數法和系數法構造輔助函數;文獻[5]用構造行列式法給出證明;文獻[6]根據Darboux定理構造另類函數;文獻[7]在通常的輔助函數上,采用區間套方法給出證明;文獻[8]總結了4種構造輔助函數的方法;文獻[9]通過復數乘法運算構造出一系列拉格朗日中值定理證明中滿足羅爾中值定理條件的輔助函數,并明確指出了柯西中值定理證明中輔助函數的構造方法;文獻[10]通過構造含參數的輔助函數證明中值定理。這些證明方法中,行列式法將線性代數用于微積分,其證明方法簡捷明了,不僅讓初學者認識并理解微分中值定理,而且為其以后的學習打下了堅實基礎。
本文應用行列式理論以及求導方法,在羅爾中值定理的基礎上,對拉格朗日中值定理和柯西中值定理進行了再一次證明,并得到了一些廣義中值定理。
1 預備知識
首先我們給出行列式的求導法則和羅爾中值定理的內容。
定理1[1]設fij(x)(i,j=1,2,…,n)為可導函數,則
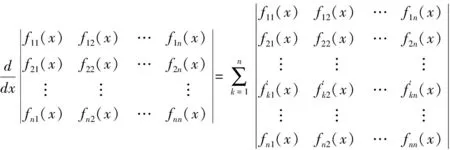
定理2 (羅爾中值定理)[1]如果函數f(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且有f(a)=f(b), 那么在(a,b)內至少存在一點ξ, 使得f′(ξ)=0。
2 中值定理的行列式法證明
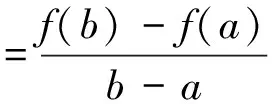
證明 構造行列式
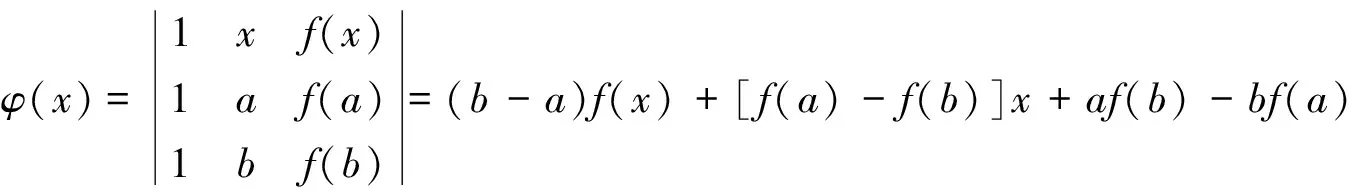
顯然φ(x)在閉區間[a,b]上連續, 開區間(a,b)內可導, 且
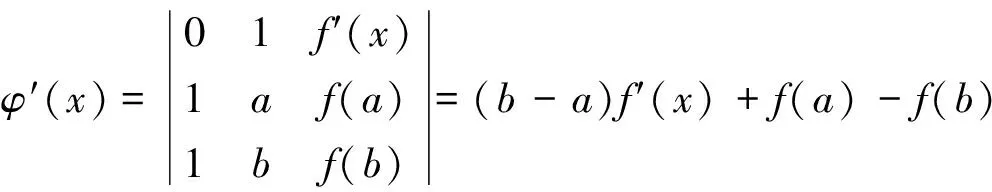
進一步計算得φ(a)=φ(b)=0。 根據羅爾中值定理知,在(a,b)內至少存在一點ξ, 使得φ′(ξ)=0,即(b-a)f′(ξ)+f(a)-f(b)=0。 故
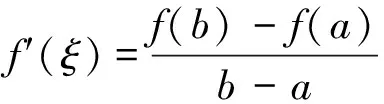
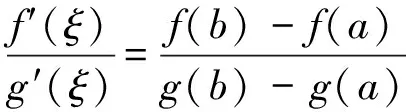
顯然φ(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且φ(a)=φ(b)=0,并有
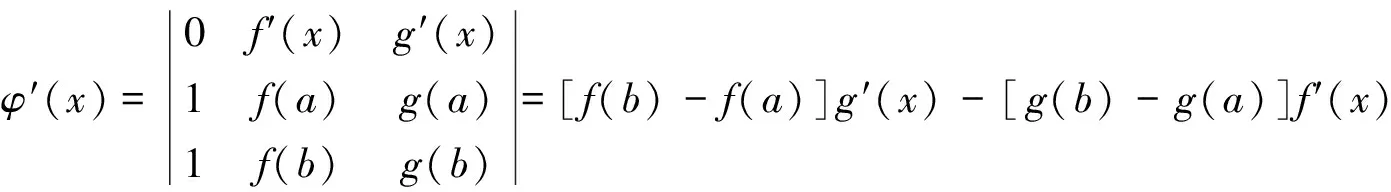
根據羅爾中值定理知,在(a,b)內至少存在一點ξ, 使得φ′(ξ)=0,即
[f(b)-f(a)]g′(ξ)=[g(b)-g(a)]f′(ξ)。
故
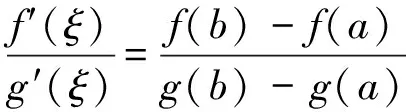
3 中值定理的推廣
定理5[5]如果函數f(x),g(x)及h(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 那么在(a,b)內至少存在一點ξ, 使得
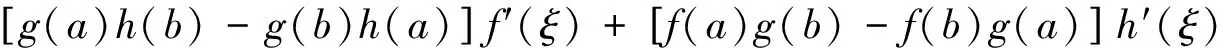
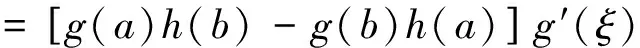
顯然φ(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且φ(a)=φ(b)=0,并有
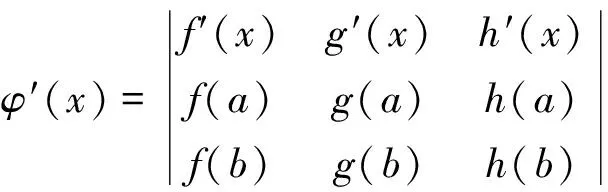
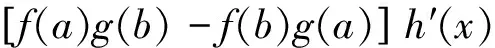
根據羅爾中值定理知,在(a,b)內至少存在一點ξ, 使得φ′(ξ)=0,即
[g(a)h(b)-g(b)h(a)]f′(ξ)+[f(a)g(b)-f(b)g(a)]h′(ξ)
=[g(a)h(b)-g(b)h(a)]g′(ξ)。
定理6[5]如果函數f(x),g(x)及h(x),p(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 那么在(a,b)內至少存在一點ξ, 使得
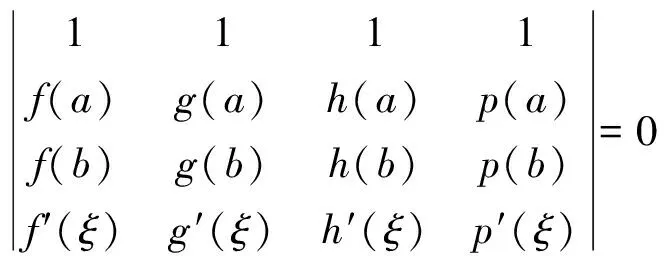
顯然φ(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且φ(a)=φ(b)=0。
根據羅爾中值定理知,在(a,b)內至少存在一點ξ, 使得φ′(ξ)=0,即
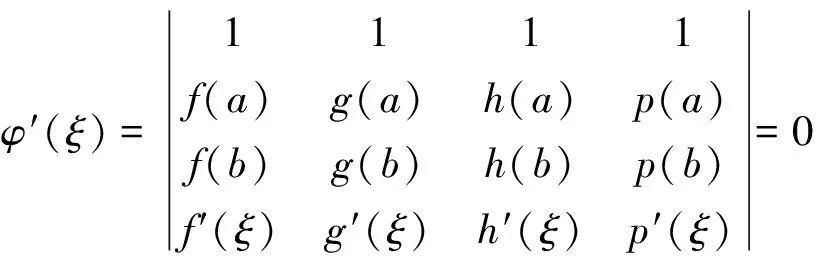
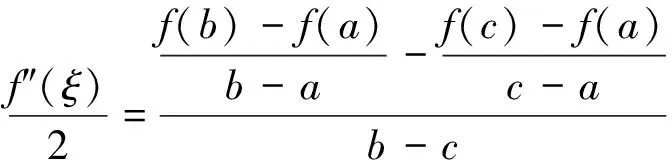
顯然φ(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且φ(a)=φ(c)=φ(b)=0,并有
根據羅爾中值定理知,至少存在點α∈(a,c),β∈(c,b), 使得φ′(α)=φ′(β)=0。
又因為φ′(x)在閉區間[α,β]上連續, 在開區間(α,β)內可導,且
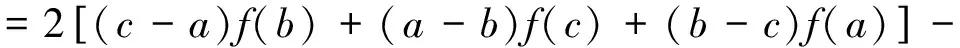
f″(x)(cb2+ac2+ba2-ca2-bc2-ab2)。
再次利用羅爾中值定理知,至少存在一點ξ∈(α,β)?(a,b),使得φ″(ξ)=0。 故
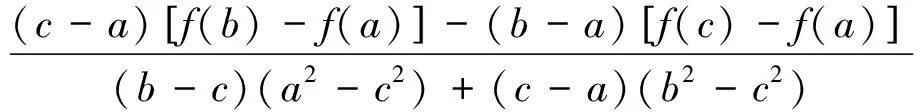
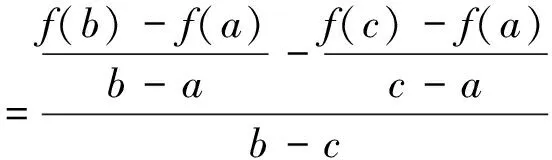
定理8 設函數f(x)在閉區間[a,b]上連續, 在開區間(a,b)內三階可導, 那么對?c,d∈(a,b),(c 顯然φ(x)在[a,b]上連續, 在(a,b)內可導, 且φ(a)=φ(c)=φ(d)=φ(b)=0。 根據羅爾中值定理知,至少存在點α∈(a,c),β∈(c,d),γ∈(d,b), 使得 φ′(α)=φ′(β)=φ′(γ)=0。 又因為φ′(x)在[α,β]及[β,γ]上分別連續, 在(α,β)及(β,γ)內可導,則至少存在點μ∈(α,β),ν∈(β,γ),使得φ″(μ)=φ″(ν)=0。 再次利用羅爾中值定理,則至少存在一點ξ∈(μ,ν),使得φ?(ξ)=0。 由于 例1 如果函數f(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且f(a)=f(b), 那么在(a,b)內至少存在一點ξ, 使等式f(a)=ξf′(ξ)+f(ξ)成立。 顯然φ(x)在閉區間[a,b]上連續,在開區間(a,b)內可導,且φ(a)=φ(b)=0,并有 根據羅爾中值定理知,在(a,b)內至少存在一點ξ, 使得φ′(ξ)=0,即 f(a)-ξf′(ξ)-f(ξ)=0。 從而,f(a)=ξf′(ξ)+f(ξ)。 特別地,當f(a)=f(b)=0時,有ξf′(ξ)+f(ξ)=0。 例2 如果函數f(x)及g(x)在閉區間[a,b](ab>0)上連續, 在開區間(a,b)內可導, 且g′(x)在(a,b)內的每一點處均不為0, 那么在(a,b)內至少存在一點ξ, 使得 顯然φ(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且φ(a)=φ(b)=0,并有 根據羅爾中值定理知,在(a,b)內至少存在一點ξ, 使得φ′(ξ)=0,即 故 顯然φ(x)在閉區間[a,b]上連續, 在開區間(a,b)內可導, 且φ(a)=φ(b)=0,并有 根據羅爾中值定理知,在(a,b)內至少存在一點ξ, 使得φ′(ξ)=0,即 由羅爾中值定理知,在區間[a,1]上,至少存在一點ξ∈(a,1)?(0,1), 使得φ′(ξ)=0,即 f(ξ)+ξf′(ξ)=0。 [1] 同濟大學數學教研室.高等數學:上冊[M].第6版.北京:高等教育出版社,2007. [2] 同濟大學數學教研室.高等數學:下冊[M].第6版.北京:高等教育出版社,2007. [3] 朱永忠,鄭蘇娟.高等數學:上冊[M].北京:科學出版社,2008. [4] 劉文武.兩個微分中值定理證明中輔助函數作法探討[J].數學的實踐與認識,2005,35(8):242-247. [5] 楊耕文.用行列式法證明微分中值定理[J].洛陽大學學報,2006,21(4):49-52. [6] 王秀玲.微分中值定理的另類證明與應用[J].安慶師范學院學報(自然科學版),2010,16(4):93-95. [7] 王家軍.微分中值定理的另類證明與推廣[J].大學數學,2008,24(4):169-171. [8] 余麗.微分中值定理的證明及應用中的輔助函數構造[J].重慶三峽學院學報,2014,30(3):21-24. [9] 宋振云,陳少元,涂瓊霞.微分中值定理證明中輔助函數的構造[J].高師理科學刊,2009,29(2):10-13. [10] 程建玲.微分中值定理的證明及推廣[J].棗莊學院學報,2014,31(5):63-66. 【責任編輯 牛懷崗】 TheProofsofMeanValueTheoremsbyUsingDeterminantMethodandExtension WANGWen-hua1a,CHENZheng-li1b,LIWei2 (1a.SchoolofEthnicNationalitiesEducation;1b.SchoolofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi’an710062,China;2.CollegeofScience,EngineeringUniversityofCAPE,Xi’an710078,China) Firstly,according to Rolle mean value theorem,the determinants to reprove the Lagrange mean value theorem and the Cauchy theorem are constructed.Secondly,the mean value theorems of three functions and four functions are established,respectively,as well as the generalized mean value theorems of high order differential function are obtained.Finally,several examples are showed to illustrate the application of the determinant method to solve the problem. determinant; derivative; mean-value theorem O151.22 A 1009-5128(2017)08-0026-07 2017-01-15 國家自然科學基金項目:量子絕熱計算的理論與應用(11601300);國家自然科學基金項目:PT-對稱量子系統的基礎理論研究(11571213);國家自然科學基金項目:線性算子的譜結構及其擾動分析(11471200);國家自然科學基金項目:多體量子關聯的動力學與時間演化(11401359);國家自然科學基金項目:量子態分類與量子絕熱逼近中的算子論方法(11371012);中央高校基本科研業務費項目:無限維絕熱量子計算模型(GK201703093) 王文華(1987—),女,陜西渭南人,陜西師范大學民族教育學院講師,理學博士,主要從事算子理論與量子信息研究;陳崢立(1973—),男,陜西西安人,陜西師范大學數學與信息科學學院副教授,理學博士,主要從事算子代數與量子信息研究。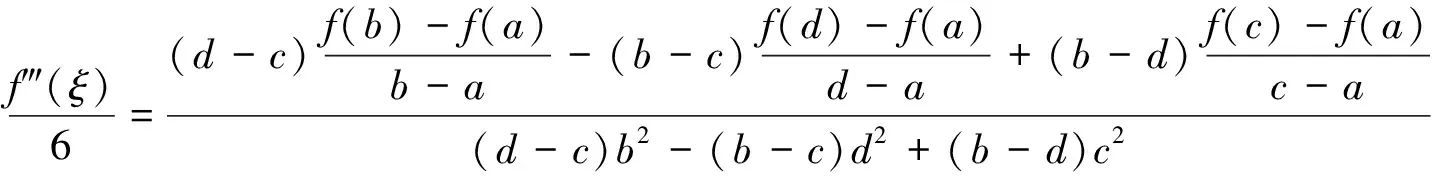
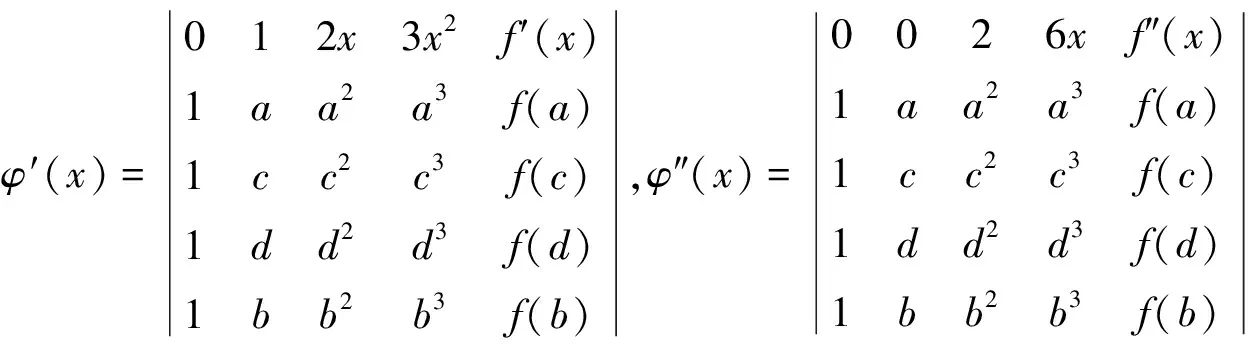
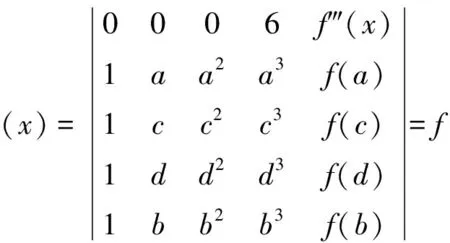
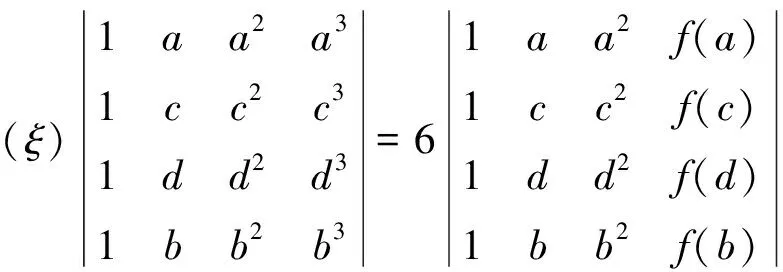
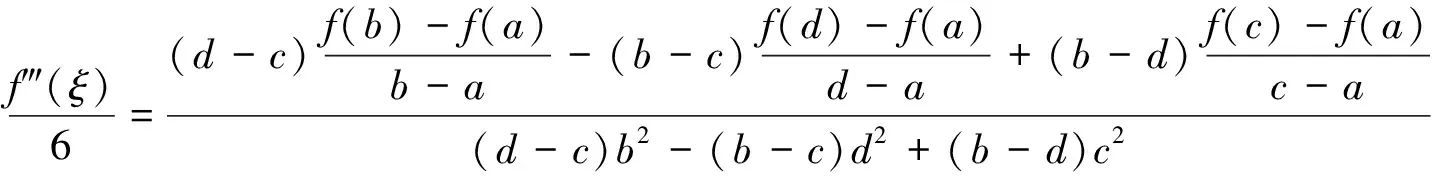
4 應用