磁流變阻尼器動力性能測試與建模
梅 真, 高毅超, 郭子雄
(1.華僑大學(xué)土木工程學(xué)院 廈門,361021) (2.福建省結(jié)構(gòu)工程與防災(zāi)重點實驗室 廈門,361021)
?
磁流變阻尼器動力性能測試與建模
梅 真1,2, 高毅超1,2, 郭子雄1,2
(1.華僑大學(xué)土木工程學(xué)院 廈門,361021) (2.福建省結(jié)構(gòu)工程與防災(zāi)重點實驗室 廈門,361021)
建立磁流變阻尼器精確的力學(xué)模型是進(jìn)行磁流變阻尼減振結(jié)構(gòu)反應(yīng)分析與設(shè)計并取得良好振動控制效果的一個重要前提。首先,對一個最大出力為10kN的磁流變阻尼器進(jìn)行動力性能測試;其次,基于試驗結(jié)果分別建立該阻尼器的參數(shù)化與非參數(shù)化動力學(xué)模型,并對所建立模型的有效性進(jìn)行驗證;最后,對兩種不同建模方式的結(jié)果進(jìn)行對比分析。結(jié)果表明,建立的參數(shù)化模型——雙曲正切滯回模型能夠有效地描述磁流變阻尼器的動力特性;非參數(shù)化模型——反向傳播(back propagation,簡稱BP)神經(jīng)網(wǎng)絡(luò)正向、逆向力學(xué)模型具有良好的訓(xùn)練樣本擬合度、泛化能力和抗噪性能;在試驗數(shù)據(jù)擬合度上,BP神經(jīng)網(wǎng)絡(luò)模型要好于雙曲正切滯回模型,但后者阻尼力表達(dá)式形式簡單,更易于程序化。
磁流變阻尼器; 動力性能測試; 雙曲正切滯回模型; BP神經(jīng)網(wǎng)絡(luò)模型
引 言
磁流變阻尼器是基于磁流變液的磁流變效應(yīng)制成的一種半主動減振裝置。它具有結(jié)構(gòu)簡單、動態(tài)范圍寬、響應(yīng)速度快、阻尼力大且連續(xù)順逆可調(diào)等優(yōu)點,被認(rèn)為是具有良好工程應(yīng)用前景的減振裝置之一[1]。采用磁流變阻尼器進(jìn)行結(jié)構(gòu)振動控制時,建立其精確的力學(xué)模型是結(jié)構(gòu)-控制系統(tǒng)設(shè)計以及取得良好振動控制效果的關(guān)鍵因素之一。
磁流變阻尼器動力學(xué)模型主要有參數(shù)化模型和非參數(shù)化模型兩種。參數(shù)化模型大多基于磁流變阻尼器動力性能測試得到的阻尼力-位移及阻尼力-速度試驗曲線,基于曲線擬合的辦法給出阻尼力數(shù)學(xué)表達(dá)式。比較有代表性的參數(shù)化模型有Bingham模型[2]、非線性雙黏性滯回模型[3]、Bouc-Wen模型[2]、現(xiàn)象模型[2,4]、修正的Dahl模型[5]、帶質(zhì)量元素的溫度唯象模型[6]、雙Sigmoid模型[7]及多項式模型[8]等。非參數(shù)化模型同樣是基于磁流變阻尼器動力性能測試試驗數(shù)據(jù),大多采用神經(jīng)網(wǎng)絡(luò)、模糊邏輯等識別方法建模,如神經(jīng)網(wǎng)絡(luò)模型[9]、模糊模型[10]及神經(jīng)-模糊模型[11]等。此外,還可以將以上兩種建模方式相結(jié)合,提出新的磁流變阻尼器非線性模型[12]。以上參數(shù)化和非參數(shù)化建模過程中并未對磁流變液的磁流變效應(yīng)產(chǎn)生機(jī)制以及磁流變阻尼器的阻尼力連續(xù)順逆可調(diào)等方面進(jìn)行物理學(xué)深層次考量,而僅僅是從現(xiàn)象學(xué)的角度,以磁流變阻尼器宏觀動力學(xué)性能的精確描述為建模的主要目標(biāo)。同時注意到,磁流變液的磁流變效應(yīng)產(chǎn)生的機(jī)理復(fù)雜,并且磁流變阻尼器的力學(xué)性能受到輸入電流、外激勵性質(zhì)等因素的影響,其動態(tài)本構(gòu)關(guān)系非常復(fù)雜。因此,目前的磁流變阻尼器建模方式通常基于阻尼器力學(xué)性能試驗結(jié)果建立其動力學(xué)模型。
筆者對一個最大出力為10kN的磁流變阻尼器進(jìn)行不同振幅與頻率正弦位移激勵下的動力性能測試。基于試驗結(jié)果,建立該阻尼器的參數(shù)化模型——雙曲正切滯回模型以及非參數(shù)化模型——BP神經(jīng)網(wǎng)絡(luò)正向和逆向力學(xué)模型,并對所建立模型的有效性進(jìn)行驗證。最后,對兩種不同建模方式的結(jié)果進(jìn)行對比分析。
1 磁流變阻尼器動力性能測試
對MRD-100-10型磁流變阻尼器進(jìn)行研究,如圖1所示。該阻尼器主要由缸體、活塞、磁流變液以及電磁線圈組成,設(shè)計最大出力為10 kN,缸體外直徑為100 mm,安裝長度為670 mm。其行程為±55 mm,最大輸入電流為2.0 A,能耗為20 W。
磁流變阻尼器動力性能測試的主要試驗設(shè)備為電液伺服材料試驗機(jī)。試驗時,試驗機(jī)的主動夾頭驅(qū)動阻尼器的活塞,使其相對于缸體以固定的頻率和振幅作簡諧運動,同時由直流穩(wěn)定電源對該阻尼器輸入某一定常電流。以不同的簡諧位移激勵振幅與頻率以及輸入電流進(jìn)行組合,對磁流變阻尼器進(jìn)行不同工況下的動力性能測試,見表1,以研究外激勵的性質(zhì)及輸入電流的大小0,0.5,1.0,1.5 A對阻尼器力學(xué)性能的影響。

圖1 動力性能測試試驗裝置Fig.1 Experimental setup for dynamic testing
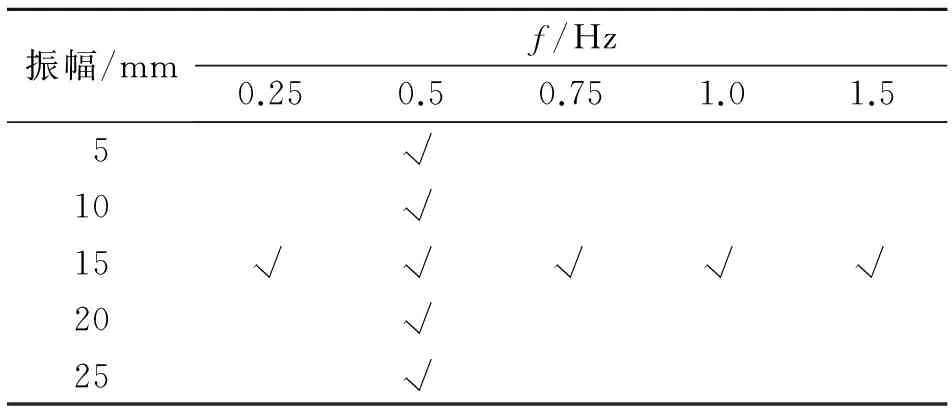
振幅/mmf/Hz0.250.50.751.01.55√10√15√√√√√20√25√
不同測試工況下,磁流變阻尼器部分試驗結(jié)果如圖2、圖3所示。阻尼器活塞相對于缸體運動的速度是通過對記錄的位移數(shù)據(jù)進(jìn)行數(shù)值微分計算得到的,且所有試驗數(shù)據(jù)均進(jìn)行過濾波處理。由圖可以看出:該阻尼器滯回曲線飽滿,耗能能力強(qiáng);阻尼力-速度曲線表現(xiàn)出較為復(fù)雜的非線性滯回特性;最大阻尼力隨輸入電流(不超過最大輸入電流2 A)的增大而增大,且兩者大體上呈線性關(guān)系;外激勵的性質(zhì)(即簡諧位移激勵的振幅和頻率)對阻尼器動力性能有明顯影響。
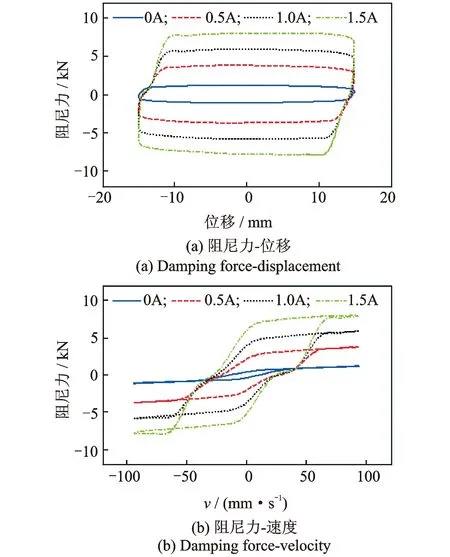
圖2 振幅為15.0 mm、頻率為1.0 Hz簡諧激勵下的試驗曲線Fig.2 Experimentally measured curves for 1.0 Hz sinusoidal excitation with amplitude of 15.0 mm
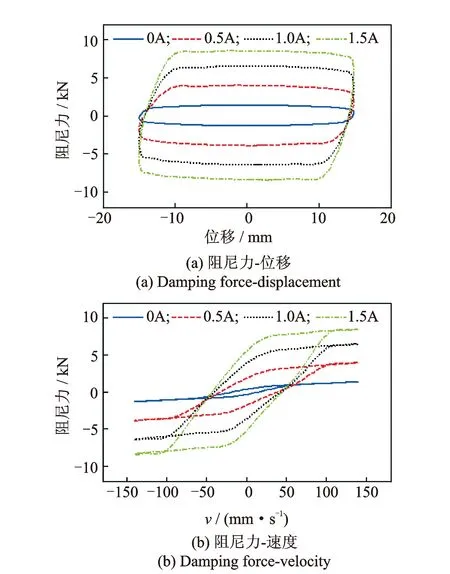
圖3 振幅為15.0 mm、頻率為1.5 Hz簡諧激勵下的試驗曲線Fig.3 Experimentally measured curves for 1.5 Hz sinusoidal excitation with amplitude of 15.0 mm
2 參數(shù)化動力學(xué)建模——雙曲正切滯回模型
磁流變阻尼器參數(shù)化動力學(xué)模型一般采用曲線擬合的辦法建立。觀察圖2、圖3中阻尼力-速度曲線不難看出,各測試工況試驗曲線均由上行和下行兩條單值曲線組成,且這兩條單值曲線的形狀與雙曲正切函數(shù)的曲線形狀均較為接近。鑒于此,金江等[13]提出磁流變阻尼器雙曲正切滯回模型,即阻尼力f可表示為
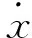
(1)

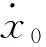
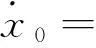
(4)

(5)

為驗證所建立雙曲正切滯回模型的有效性,將磁流變阻尼器動力性能測試試驗數(shù)據(jù)與該模型分析結(jié)果進(jìn)行對比。限于篇幅,只給出其中1組典型工況下試驗數(shù)據(jù)與模型分析結(jié)果的對比,如圖4所示。
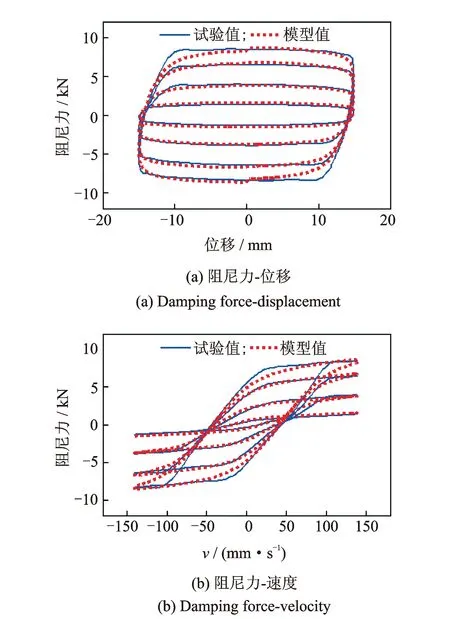
圖4 雙曲正切滯回模型驗證Fig.4 Validation of hyperbolic tangent hysteresis model
由圖4可見,試驗實測數(shù)據(jù)與雙曲正切滯回模型的計算結(jié)果較為吻合。為進(jìn)行定量誤差分析,定義如下的2-范數(shù)相對誤差
e=‖xExp(t)-xAna(t)‖/‖xExp(t)‖×100%
(6)
其中:xExp(t)與xAna(t)分別為t時刻的試驗實測值與模型分析值。
誤差分析結(jié)果表明,圖4中阻尼力的2-范數(shù)相對誤差為7.07%。由此可見,筆者建立的雙曲正切滯回模型能夠較好地刻畫磁流變阻尼器的阻尼力-位移以及阻尼力-速度曲線,即能夠?qū)ψ枘崞鞯膭恿μ匦赃M(jìn)行較為準(zhǔn)確的定量把握。
3 非參數(shù)化動力學(xué)建模——BP神經(jīng)網(wǎng)絡(luò)模型
人工神經(jīng)網(wǎng)絡(luò)因具有非常好的非線性逼近能力,可應(yīng)用于非線性系統(tǒng)的辨識。其中,BP神經(jīng)網(wǎng)絡(luò)是目前應(yīng)用最為廣泛的神經(jīng)網(wǎng)絡(luò)模型之一,故筆者將基于BP神經(jīng)網(wǎng)絡(luò)建立磁流變阻尼器的正向和逆向力學(xué)模型。
3.1 BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型
磁流變阻尼器的阻尼力是輸入電流以及缸體與活塞相對運動位移及速度的函數(shù),且阻尼器在工作過程中是一個動態(tài)系統(tǒng)。然而,BP神經(jīng)網(wǎng)絡(luò)本質(zhì)上是一類靜態(tài)的非線性映射,必須將動態(tài)特性引入磁流變阻尼器的BP神經(jīng)網(wǎng)絡(luò)模型,其中最直接的方法是根據(jù)系統(tǒng)過去的輸入和輸出,增加網(wǎng)絡(luò)的輸入。基于以上考慮,最終確定的BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型具有圖5所示的網(wǎng)絡(luò)結(jié)構(gòu),即磁流變阻尼器當(dāng)前時刻的阻尼力f(t)可表示為
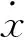
(7)
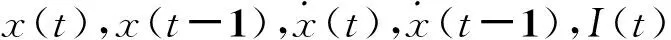

圖5 BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型的網(wǎng)絡(luò)結(jié)構(gòu)Fig.5 Configuration of forward neural network model
磁流變阻尼器動力性能測試中獲得的部分試驗數(shù)據(jù)將應(yīng)用于BP神經(jīng)網(wǎng)絡(luò)模型的訓(xùn)練與測試。與圖2、圖3相對應(yīng)的試驗數(shù)據(jù)分別用作訓(xùn)練樣本及測試樣本。筆者采用貝葉斯正則化算法(trainbr),而非常見的Levenberg-Marquardt算法(trainlm)進(jìn)行BP神經(jīng)網(wǎng)絡(luò)模型的訓(xùn)練。這是由于經(jīng)前一種算法訓(xùn)練得到的神經(jīng)網(wǎng)絡(luò)較少出現(xiàn)因“過度訓(xùn)練”而導(dǎo)致“過度擬合”的情況,且在泛化能力及抗噪性能方面往往表現(xiàn)更優(yōu)。圖5中BP神經(jīng)網(wǎng)絡(luò)模型隱含層和輸出層的激活函數(shù)分別為雙曲正切S型函數(shù)(tansig)和線性函數(shù)(purelin)。
為驗證已訓(xùn)練BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型的有效性,以下將從訓(xùn)練樣本的擬合程度、網(wǎng)絡(luò)的泛化能力及抗噪性能三個方面分別進(jìn)行分析。
BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型的訓(xùn)練數(shù)據(jù)與網(wǎng)絡(luò)輸出的對比如圖6所示,阻尼力的2-范數(shù)相對誤差為0.32%。由此可見,所建立的BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型對訓(xùn)練樣本具有非常高的擬合度。
BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型的測試數(shù)據(jù)與網(wǎng)絡(luò)輸出的對比如圖7所示,阻尼力的2-范數(shù)相對誤差為1.53%,僅較之于訓(xùn)練數(shù)據(jù)與網(wǎng)絡(luò)輸出的2-范數(shù)相對誤差略大。因此,經(jīng)貝葉斯正則化算法訓(xùn)練過的BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型對測試樣本同樣具有非常好的預(yù)測能力,即泛化能力優(yōu)異。

圖6 正向力學(xué)模型訓(xùn)練數(shù)據(jù)與網(wǎng)絡(luò)輸出對比Fig.6 Comparison of training data and network outputs
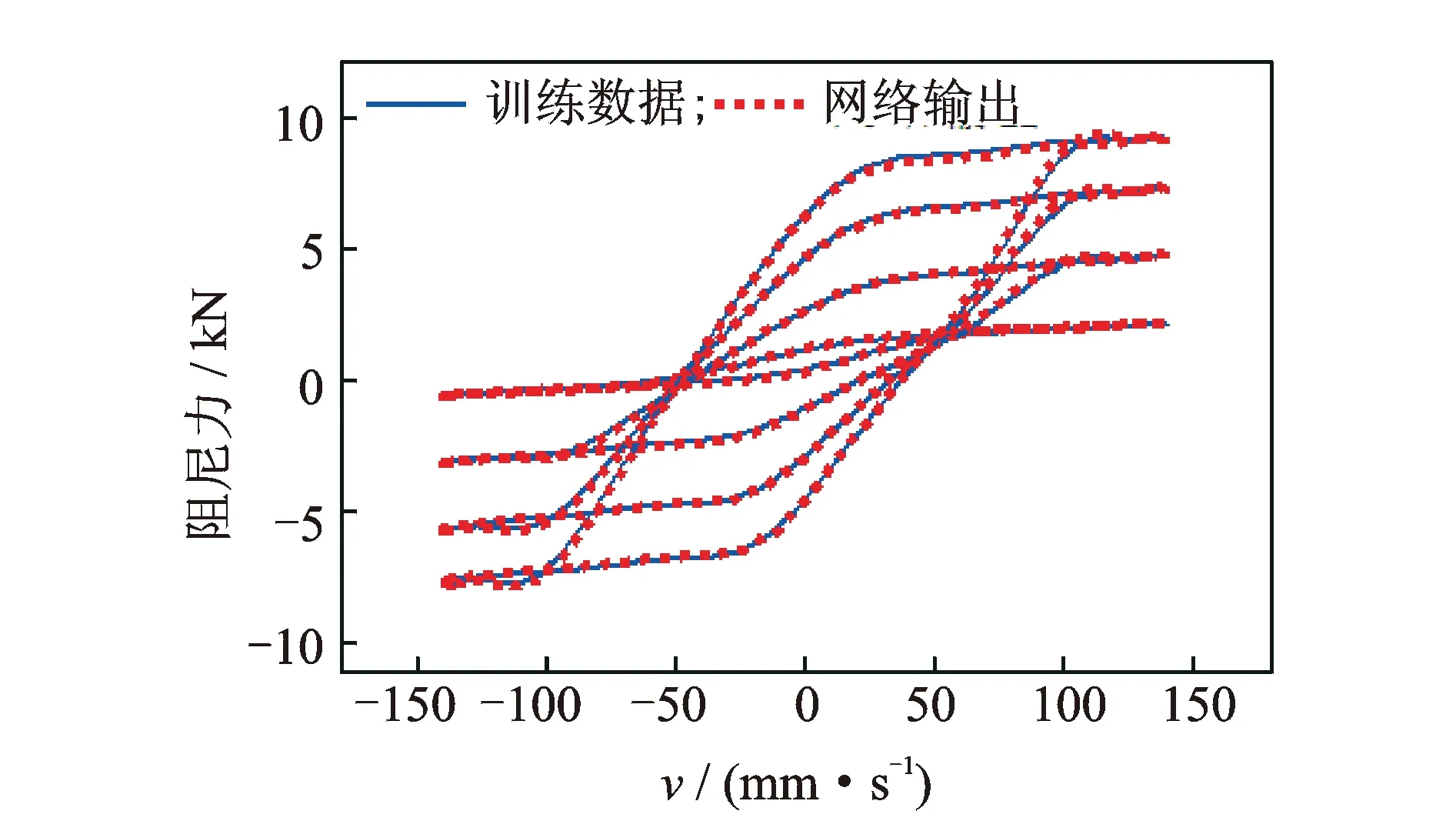
圖7 正向力學(xué)模型測試數(shù)據(jù)與網(wǎng)絡(luò)輸出對比Fig.7 Comparison of test data and network outputs
以上BP神經(jīng)網(wǎng)絡(luò)建模及性能分析中所采用的訓(xùn)練及測試樣本均為濾波處理后的試驗數(shù)據(jù),而觀測噪聲在實際反饋控制中是普遍存在的,并且它對控制品質(zhì)也會產(chǎn)生一定影響。因此,有必要對BP神經(jīng)網(wǎng)絡(luò)力學(xué)模型的抗噪性能進(jìn)行分析,這一點在已有的關(guān)于磁流變阻尼器神經(jīng)網(wǎng)絡(luò)建模的文獻(xiàn)中卻經(jīng)常被忽視。對于單輸出系統(tǒng),系統(tǒng)的統(tǒng)計靈敏度[14-15]可定義為
(8)
其中:σ為系統(tǒng)輸入擾動的標(biāo)準(zhǔn)差;var(Δy)為由輸入擾動引起的系統(tǒng)輸出誤差的方差值。
本研究靈敏度分析中,分別考慮加性和乘性這兩種輸入擾動對BP神經(jīng)網(wǎng)絡(luò)模型輸出誤差的影響,且假定加性及乘性輸入擾動分別為加性和乘性白噪聲過程。BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型的統(tǒng)計靈敏度分析結(jié)果如圖8所示。
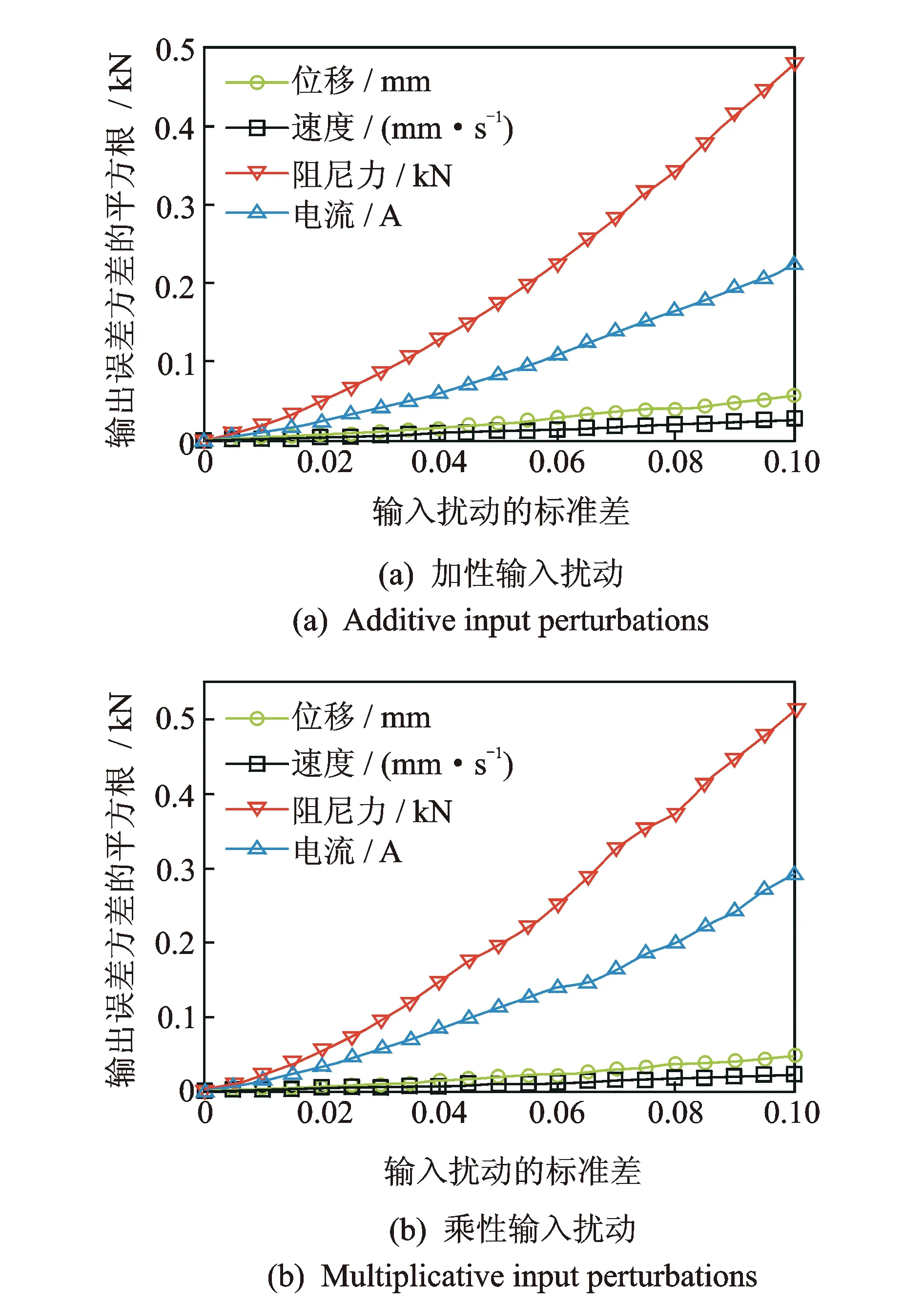
圖8 正向力學(xué)模型統(tǒng)計靈敏度Fig.8 Statistical sensitivities for forward model
由圖8可知,當(dāng)輸入擾動的幅度較小時,由此引起的BP神經(jīng)網(wǎng)絡(luò)模型輸出誤差并不明顯。但是隨著輸入擾動幅度的增大,輸出統(tǒng)計靈敏度快速增大。同時注意到,不同的輸入量在同一幅度噪聲擾動下,對BP神經(jīng)網(wǎng)絡(luò)模型輸出誤差的影響不盡相同,其中,阻尼力擾動引起的統(tǒng)計靈敏度最為突出。因此,對于所建立的磁流變阻尼器BP神經(jīng)網(wǎng)絡(luò)正向力學(xué)模型,在實際工程應(yīng)用中可以考慮對阻尼力反饋信號進(jìn)行降噪處理,以減小觀測噪聲對實時控制系統(tǒng)帶來的不利影響。此外,由分析結(jié)果可知,兩種不同性質(zhì)輸入擾動(即加性與乘性輸入擾動)下的統(tǒng)計靈敏度分析結(jié)果較為接近。
3.2 BP神經(jīng)網(wǎng)絡(luò)逆向力學(xué)模型
上面基于BP神經(jīng)網(wǎng)絡(luò)建立了磁流變阻尼器的正向力學(xué)模型。然而,當(dāng)由控制算法確定的控制量是阻尼器的阻尼力而非輸入電流時,需要通過該阻尼器的逆向力學(xué)模型由期望的阻尼力計算出相應(yīng)的控制電流。磁流變阻尼器逆向力學(xué)模型建模中所采用的訓(xùn)練及測試數(shù)據(jù)與正向力學(xué)模型建模中的相同,只是輸入量與輸出量有所區(qū)別。BP神經(jīng)網(wǎng)絡(luò)逆向力學(xué)模型的網(wǎng)絡(luò)結(jié)構(gòu)如圖9所示,即磁流變阻尼器當(dāng)前時刻的輸入電流I(t)可表示為
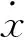
(9)
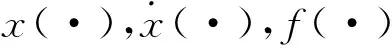
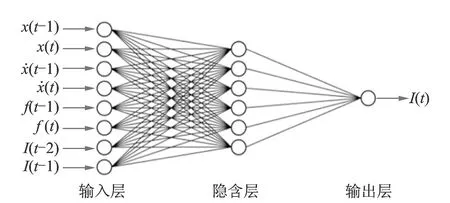
圖9 BP神經(jīng)網(wǎng)絡(luò)逆向力學(xué)模型的網(wǎng)絡(luò)結(jié)構(gòu)Fig.9 Configuration of inverse neural network model
與正向力學(xué)模型相同,逆向力學(xué)模型也采用貝葉斯正則化算法(trainbr)進(jìn)行訓(xùn)練,隱含層和輸出層的激活函數(shù)分別為雙曲正切S型函數(shù)(tansig)和線性函數(shù)(purelin)。訓(xùn)練完畢后,BP神經(jīng)網(wǎng)絡(luò)逆向力學(xué)模型的訓(xùn)練數(shù)據(jù)與網(wǎng)絡(luò)輸出的對比如圖10所示,輸入電流的2-范數(shù)相對誤差為0.03%。逆向力學(xué)模型的測試數(shù)據(jù)與網(wǎng)絡(luò)輸出的對比如圖11所示,輸入電流的2-范數(shù)相對誤差為0.75%。由此可知,訓(xùn)練過的磁流變阻尼器逆向力學(xué)模型具有很好的訓(xùn)練樣本擬合度和泛化性能。
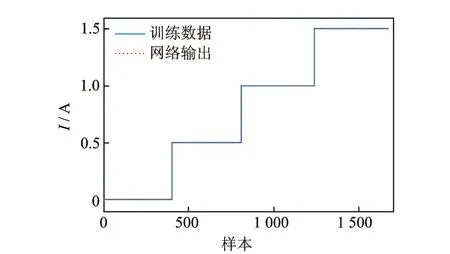
圖10 逆向力學(xué)模型訓(xùn)練數(shù)據(jù)與網(wǎng)絡(luò)輸出對比Fig.10 Comparison of training data and network outputs
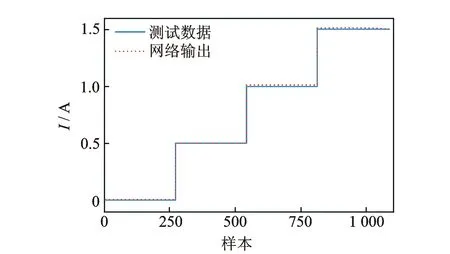
圖11 逆向力學(xué)模型測試數(shù)據(jù)與網(wǎng)絡(luò)輸出對比Fig.11 Comparison of test data and network outputs

圖12 逆向力學(xué)模型統(tǒng)計靈敏度Fig.12 Statistical sensitivities for inverse model
為研究BP神經(jīng)網(wǎng)絡(luò)逆向力學(xué)模型的抗噪性能,分別考慮加性和乘性這兩種輸入擾動,對該模型的統(tǒng)計靈敏度進(jìn)行了分析,分析結(jié)果如圖12所示。由圖可知,與其他輸入量相比,當(dāng)磁流變阻尼器的控制電流受噪聲擾動時,將會引起B(yǎng)P神經(jīng)網(wǎng)絡(luò)逆向力學(xué)模型相對最大的輸出誤差。
4 兩種建模方式的比較
兩種建模方法都是從現(xiàn)象學(xué)的角度、以磁流變阻尼器宏觀動力學(xué)性能的精確描述為建模的主要目標(biāo)。若以模型預(yù)測結(jié)果與試驗實測數(shù)據(jù)的擬合程度評價建模效果,由2-范數(shù)相對誤差數(shù)據(jù)對比可知,非參數(shù)化模型(BP神經(jīng)網(wǎng)絡(luò)模型)的建模精度相對于參數(shù)化模型(雙曲正切滯回模型)要更高。由BP神經(jīng)網(wǎng)絡(luò)可以同時建立磁流變阻尼器的正向和逆向動力學(xué)模型,因此在控制器設(shè)計時可根據(jù)實際需要選用。然而,與筆者建立的雙曲正切滯回模型一樣,已有文獻(xiàn)中建立的參數(shù)化模型大多為正向力學(xué)模型,而由參數(shù)化正向力學(xué)模型一般很難直接得到相應(yīng)的逆向力學(xué)模型。
筆者建立的參數(shù)化模型——雙曲正切滯回模型的阻尼力表達(dá)式形式簡單,其中的4個基本參數(shù)物理意義明確且便于識別。因此,在結(jié)構(gòu)-控制系統(tǒng)設(shè)計時采用雙曲正切滯回模型要比BP神經(jīng)網(wǎng)絡(luò)模型能更好地與分析軟件,特別是專業(yè)設(shè)計軟件相融合,以便設(shè)計人員進(jìn)行一體化分析。由于雙曲正切滯回模型能夠?qū)Υ帕髯冏枘崞鞯膭恿μ匦赃M(jìn)行較為準(zhǔn)確的定量描述,結(jié)構(gòu)-控制系統(tǒng)的整體分析精度能夠滿足工程要求。
5 結(jié) 論
1) 本研究中阻尼器的滯回曲線飽滿,最大阻尼力隨輸入電流(不超過最大輸入電流2 A)的增大而增大,且阻尼力-速度曲線表現(xiàn)出較為復(fù)雜的非線性滯回特性。
2) 參數(shù)化模型——雙曲正切滯回模型,阻尼力表達(dá)式形式簡單,其中的4個基本參數(shù)物理意義明確且便于識別,分析表明該模型能有效刻畫磁流變阻尼器的動力特性。
3) 非參數(shù)化模型——BP神經(jīng)網(wǎng)絡(luò)正向、逆向力學(xué)模型能分別準(zhǔn)確地預(yù)測磁流變阻尼器的阻尼力與輸入電流,且均具有良好的訓(xùn)練樣本擬合度、泛化能力和抗噪性能。
4) 在試驗數(shù)據(jù)擬合度上,BP神經(jīng)網(wǎng)絡(luò)模型要好于雙曲正切滯回模型,但后者阻尼力表達(dá)式形式簡單,更易于程序化。
[1] Jung H J, Spencer Jr B F, Ni Yiqing, et al. State-of-the-art of semiactive control systems using MR fluid dampers in civil engineering applications[J]. Structural Engineering and Mechanics, 2004,17(3-4):493-526.
[2] Spencer Jr B F, Dyke S J, Sain M K, et al. Phenomenological model for magnetorheological dampers[J]. Journal of Engineering Mechanics, 1997,123(3):230-238.
[3] Wereley N M, Pang Li, Kamath G M. Idealized hysteresis modeling of electrorheological and magnetorheological dampers[J]. Journal of Intelligent Material Systems and Structures, 1998,9(8):642-649.
[4] Yang Guangqiang. Large-scale magnetorheological fluid damper for vibration mitigation: modeling, testing and control[D]. Indiana, United States: The University of Notre Dame, 2001.
[5] 周強(qiáng),瞿偉廉.磁流變阻尼器的兩種力學(xué)模型和試驗驗證[J].地震工程與工程振動,2002,22(4):144-150.
Zhou Qiang, Qu Weilian. Two mechanic models for magnetorheological damper and corresponding test verification [J]. Earthquake Engineering and Engineering Vibration, 2002,22(4):144-150. (in Chinese)
[6] 徐趙東,李愛群,程文瀼,等.磁流變阻尼器帶質(zhì)量元素的溫度唯象模型[J].工程力學(xué),2005,22(2):144-148.
Xu Zhaodong, Li Aiqun, Cheng Wenrang, et al. A temperature phenomenological model with mass element of magnetorheological damper[J]. Engineering Mechanics,2005,22(2):144-148. (in Chinese)
[7] 李秀領(lǐng),李宏男.磁流變阻尼器的雙sigmoid模型及試驗驗證[J].振動工程學(xué)報,2006,19(2):168-172.
Li Xiuling, Li Hongnan. Double-sigmoid model for magnetorheological damper and corresponding experiment verification[J]. Journal of Vibration Engineering, 2006,19(2):168-172. (in Chinese)
[8] 周鐵明,陳恩偉,陸益民,等.磁流變阻尼器的改進(jìn)多項式模型及驗證[J].振動與沖擊,2014,33(7):221-226.
Zhou Tieming, Chen Enwei, Lu Yimin, et al. Modified polynomial model and its verification for a MR damper[J]. Journal of Vibration and Shock, 2014,33(7):221-226. (in Chinese)
[9] Boada M J L, Calvo J A, Boada B L, et al. Modeling of a magnetorheological damper by recursive lazy learning[J]. International Journal of Non-Linear Mechanics, 2011,46(3):479-485.
[10]Liem D T, Truong D Q, Ahn K K. Hysteresis modeling of magnetorheological damper using self-tuning Lyapunov based fuzzy approach[J]. International Journal of Precision Engineering and Manufacturing, 2015,16(1):31-41.
[11]鄭玲,周忠永.基于自適應(yīng)神經(jīng)模糊的磁流變阻尼器非參數(shù)化建模[J].振動與沖擊,2011,30(10):25-29.
Zheng Ling, Zhou Zhongyong. Non-parametric modeling for a magneto-rheological (MR) damper based on an adaptive neuro-fuzzy inference system[J]. Journal of Vibration and Shock, 2011,30(10):25-29. (in Chinese)
[12]潘公宇,楊海,徐騰躍,等.磁流變液阻尼器試驗與建模研究[J].振動與沖擊,2015,34(6):36-40.
Pan Gongyu, Yang Hai, Xu Tengyue, et al. Tests and modeling for magneto-rheological (MR) dampers[J]. Journal of Vibration and Shock, 2015,34(6):36-40. (in Chinese)
[13]金江,劉紅梅,王海霞.磁流變阻尼器的實用計算模型[J].南通大學(xué)學(xué)報:自然科學(xué)版,2006,5(3):80-83.
Jin Jiang, Liu Hongmei, Wang Haixia. Practical calculating model of magnetorheological damper [J]. Journal of Nantong University: Natural Science Edition, 2006,5(3):80-83. (in Chinese)
[14]Choi J Y, Choi C. Sensitivity analysis of multilayer perceptron with differentiable activation functions [J]. IEEE Transactions on Neural Networks, 1992,3(1):101-107.
[15]Bernier J L, Díaz A F, Fernández F J, et al. Assessing the noise immunity and generalization of radial basis function networks[J]. Neural Processing Letters, 2003,8(1):35-48.

10.16450/j.cnki.issn.1004-6801.2017.03.021
國家自然科學(xué)基金資助項目(51409107,51608212);中國博士后科學(xué)基金資助項目(2014M551832);福建省自然科學(xué)基金資助項目(2015J01211)
2015-11-08;
2016-01-04
TU352.1; TH113
梅真,男,1983年8月生,講師。主要研究方向為結(jié)構(gòu)振動控制。曾發(fā)表《Experimental and analytical studies on stochastic seismic response control of structures with MR dampers》(《Earthquakes and Structures》2013,Vol.5,No.4)等論文。 E-mail:meizhen83@163.com

