一種基于分布中心的矢量數據零水印算法
呂文清,張黎明
(1.蘭州交通大學 測繪與地理信息學院,甘肅 蘭州 730070;2.甘肅省地理國情監測工程實驗室,甘肅 蘭州 730070)
一種基于分布中心的矢量數據零水印算法
呂文清1,2,張黎明1,2
(1.蘭州交通大學 測繪與地理信息學院,甘肅 蘭州 730070;2.甘肅省地理國情監測工程實驗室,甘肅 蘭州 730070)
針對鮮有零水印算法能同時適用于點、線、面矢量數據版權保護,提出一種基于分布中心的矢量地理空間數據零水印算法。首先,對矢量數據進行格網劃分;其次,計算格網內每個點到其算數平均值中心的距離,并將得到的距離序列與距離平均值進行比較,大于等于距離平均值,則記為1,否則為0;然后,統計格網內的0和1數量的多數,記為0或1,以此生成空間數據特征值;最后,將該特征值與置亂后的二值水印進行異或,構造出零水印圖像。實驗表明,文中算法能同時適用于點、線、面矢量數據,并且對常見的平移、縮放、裁剪、格式轉換、隨機刪點等攻擊魯棒性好。
矢量地理空間數據;算數平均值中心;零水印;魯棒性
隨著測繪地理信息行業的不斷發展,地理空間數據在地理信息、電子導航、數字城市、環境保護等領域得到廣泛應用。然而,目前GIS矢量數字產品的市場狀況十分混亂[1],侵犯版權的事件時有發生,傳統的版權保護方式已經很難適應目前的需要。一方面,地理空間數據生產成本高昂,精度高,安全級別較高;但另一方面,當前的地理空間數據主要以數字化形式保存,這在為數據拷貝和傳播提供便利的同時也使得數據的盜版使用變得極其容易[2]。數字水印技術作為近年來信息安全領域發展起來的前沿技術,在矢量地理空間數據版權保護方面得到了廣泛的重視和研究[3-7]。
目前,矢量地理空間數據水印算法主要為空域算法和頻域算法,這兩種算法都需要改變載體數據來添加水印信息,這在一定程度上影響了數據的質量,對于數據精度要求高的應用領域,可能會造成數據無法正常使用。為了在實現版權保護的同時不損害數據質量,滿足對數據高保真的要求,溫泉等人首次提出了零水印的概念,并將其應用到數字圖像版權保護中[8]。零水印是指不修改原始作品的內容,利用原始作品的重要特征構造水印,能解決水印魯棒性和不可見性之間的矛盾[9]。張佐理[10]等首次將零水印技術引入矢量地圖版權保護領域,通過統計平均分塊后各個分塊的頂點數,并利用變換和加密構造出水印圖;之后一些學者如曹劉娟[11]、孫鴻睿[9,12]等紛紛對矢量地理數據零水印進行了相應的研究,并取得了一些成果。但目前對矢量數據零水印的研究多針對某一特定類型的矢量數據,鮮有零水印算法能同時適用于點、線、面數據版權保護,因此,本文在前人研究的基礎上提出了一種同時適用于點、線、面3種矢量數據的零水印算法。
1 零水印構造方案
算法的基本思路:首先對空間數據的最小外接矩形進行平均分塊;其次計算每個格網中點到其算數平均值中心的距離和格網內所有距離的平均值;然后,將距離平均值與每個距離進行比較,若某點所對應的距離大于等于距離平均值,則記為1,否則記為0;接著統計每個格網內0和1的數量,若1的數量多于0的數量,則該格網用1表示,否則用0表示;最后將生成的二值特征序列與置亂后的水印圖像進行邏輯異或運算,從而構造出零水印圖像。零水印構造流程如圖1所示。
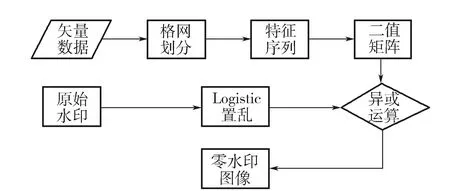
圖1 零水印構造流程
1.1 格網劃分
為更好地提取矢量地理空間數據的特征信息,反應矢量數據的局部特征,采用格網劃分的方法將頂點劃分成多個格網單元。讀取矢量數據,得到所有坐標點的最大值與最小值,即Xmin,Ymin,Xmax,Ymax,用得到的最大值點和最小值點的橫坐標和縱坐標構成矢量數據的最小外接矩形(Minimum Bounding Rectangle, MBR),最小外接矩形具有一定的穩定性,一般很少受到攻擊。以數據的MBR為劃分格網的基礎,將MBR劃分成大小相同的格網,格網劃分的大小與水印圖像的大小相同。劃分方法如圖2所示。
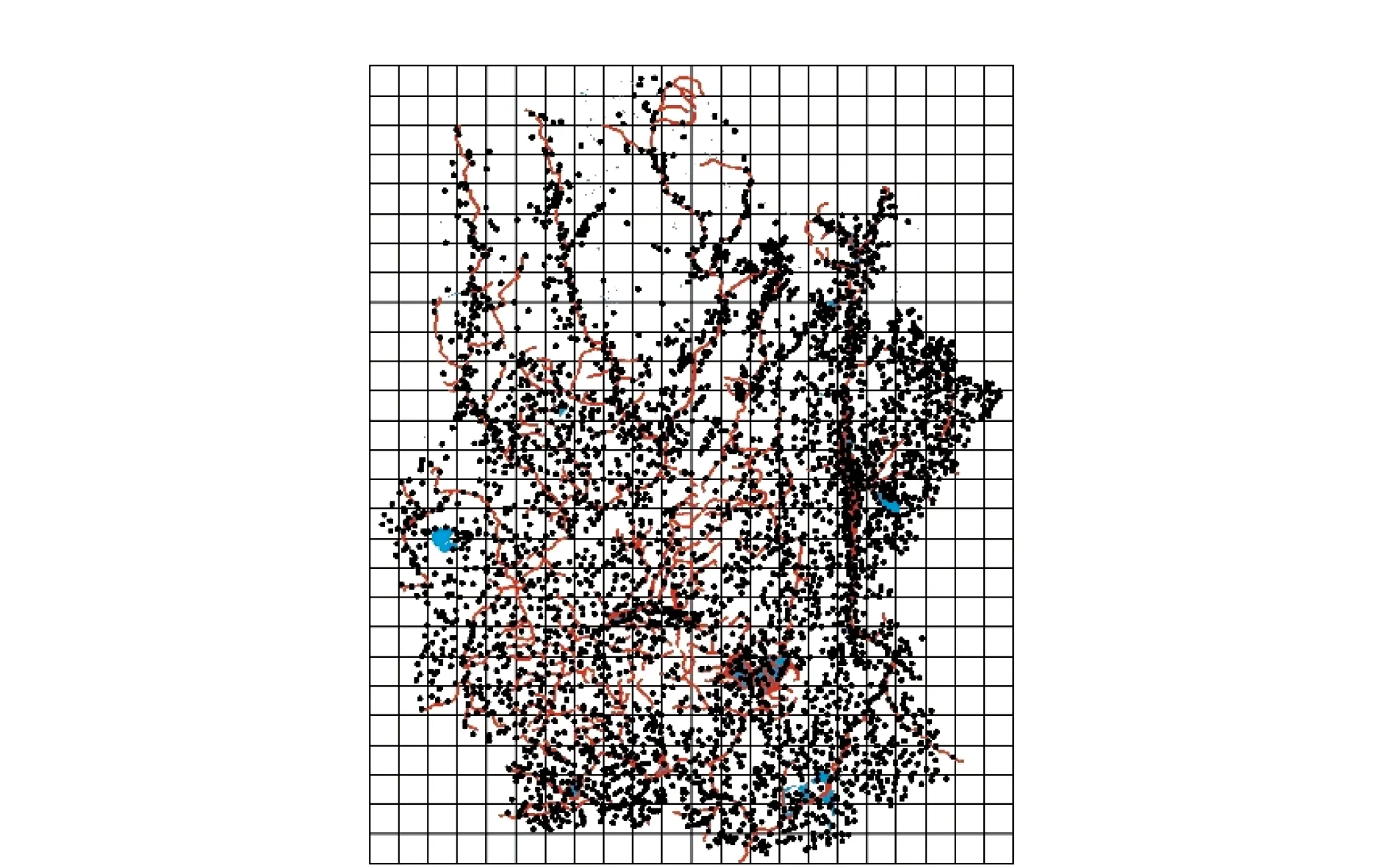
圖2 格網劃分示意圖
1.2 特征序列生成
本算法以格網為單元,每一個格網內的點可表示為
vi=(xi,yi),i=1,2,…,n.
(1)
其中:vi表示每一個坐標點,(xi,yi)表示點的坐標值,n表示頂點的個數。
1.2.1 算數平均值中心
空間分布是從總體的、全局的角度來描述空間變量和空間物體的特性[9]。其中矢量數據的分布中心是一個重要的參數,算數平均值中心是分布中心的一種,可以概略地表示分布總體的位置,其沒有考慮數據之間的差異,所得的平均中心具有隨機性。由于矢量數據并不總是規則分布的,隨機分布的狀態更為常見,計算矢量數據平均中心時會出現某些格網內沒有坐標點,需要跳過該網格,不計算該格網內的算數平均值中心。
當n≥1時計算該格網內點的平均值中心[9],記為O,計算公式為
(2)
其中:Ox,Oy分別為單元格頂點平均中心的坐標,Xi,Yi表示第i個點的X,Y坐標,n表示格網內的點數。
1.2.2 距離計算
計算每個格網內的頂點到O點的距離di,計算出di的平均值D。其中di和D的計算公式為
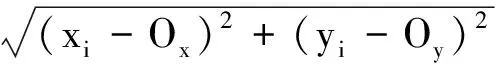
(3)
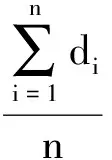
(4)
其中,n表示每個格網內的頂點個數。
1.2.3 特征矩陣生成
利用矢量數據中每個點到格網內頂點的算數平均值中心的距離來構造特征矩陣。通過比較di和D的大小生成二值序列,當di≥D時,M記為1;當di (5) 其中,M表示二值序列。 然后將得到的二值序列壓縮為64×64的二值矩陣,其大小與水印圖像大小相同。壓縮策略為統計每個格網內0和1的數量,若格網內1的個數大于0的個數,該格網的值為1,反之為0。 1.2.4 零水印圖像構造 零水印圖像的詳細構造過程描述如下: 首先將原始水印圖像進行Logistic置亂,以提高水印的安全性和保密性。算法中采用的水印圖像大小為64×64像素,原始水印圖像及置亂后的水印圖像如圖3所示。 圖3 水印圖像 然后,將得到的二值矩陣M與置亂變換后的水印圖像二值序列W進行邏輯異或運算,得到零水印圖像矩陣W′,即 W′=M⊕W. (6) 其中:M表示最終的二值矩陣,⊕表示按位異或運算,W′表示置亂后的水印圖像矩陣。 零水印的檢測是構造過程的逆,具體過程描述如下: 1)對待測數據進行格網劃分,格網大小與水印圖像大小相同。 2)計算每個格網內坐標點的算數平均值中心,并計算每個點到該平均中心的距離。 3)計算每個格網內距離的平均值,并將每個點到其相應的平均中心的距離與格網內所有坐標點對應的距離平均值進行比較,并統計大于等于距離平均值的坐標點數量和小于平均值的點數,若大于距離平均值的坐標點數占優勢,則該格網用1表示,否則為0,從而生成一個64×64的二值矩陣。 4)將零水印圖像與由待檢測數據生成的二值矩陣進行邏輯異或運算,得到置亂的水印信息,然后將其進行Logistic反置亂變換,得到最終的水印信息。 以MATLAB R2015a為平臺對零水印算法進行實驗,實驗數據分別采用雅礱江南部地區水文測站矢量點數據、河網支流矢量線數據和湖泊矢量面數據,疊加顯示效果如圖4(a)所示,其中點、線、面要素分別為382 0個、963個和414個,數據格式為ArcGIS的Shp格式,將其分別劃分成64×64固定大小的格網。實驗中用的水印為64×64像素的二值水印圖像如圖4(b)所示。點、線、面數據構造的零水印圖像如圖4(c)所示。 圖4 零水印構造實驗結果 3.1 魯棒性實驗 一個好的水印算法應當在數據經過一些改變后,水印仍具有較好的可檢測性。本文采用歸一化相關系數(Normalized Correlation Coefficient, NC)作為評價指標,對本算法進行隨機刪點、格式轉換、縮放和平移等攻擊,以驗證該算法的魯棒性。NC[12]計算公式為 (7) 測試結果如表1所示,對點、線、面數據進行隨機刪點、平移、縮放、格式轉換攻擊后,本算法仍能較好地提取水印信息,檢測到的水印圖像與版權標識圖像的相似度較高。但由于算法是基于格網劃分構造水印的,因此無法抵抗旋轉攻擊。 3.2 抗裁剪攻擊實驗 在研究和實際應用操作中通常要對數據進行裁剪,以獲得研究區的數據,裁剪操作通常較為頻繁,但這卻會造成水印信息的提取異常。為此,水印算法須有能力抵抗一定的裁剪攻擊,從而滿足實際需要,增強算法的實用性。 圖5 裁剪攻擊實驗結果 實驗通過模擬研究中的裁剪操作,對研究區內的某一島內數據按要素進行裁剪,以獲得符合要求的數據。研究區原始數據及島要素疊加顯示效果如圖5(a)所示,對原始矢量點、線、面數據用島要素進行裁剪,裁剪后數據疊加效果如圖5(b)所示。然后利用裁剪后剩余數據檢測零水印,以測驗算法對裁剪攻擊的魯棒性。裁剪攻擊后提取到的點、線、面數據的水印信息如圖5(c)所示,實驗提取到的點、線、面數據的水印圖像與版權標識圖像的相似度分別為:0.888 2,0.994 9,0.995 1。 由實驗可知,本算法對裁剪攻擊具有魯棒性,但因實驗中矢量點數據數據量較小,因此,抗裁剪攻擊實驗時實驗效果不如線、面矢量數據,但檢測到的水印信息與版權標識水印圖像相似度仍高于88%,所以算法對數據量較小的矢量地理數據版權保護同樣具有較好的適用性。 本文提出了一種針對矢量數據的零水印算法,通過格網劃分并計算每個點到相應格網內頂點的算數平均值中心的距離和格網內的距離平均值進行比較,將矢量數據映射為和水印大小相同的二值序列,再通過與置亂后的水印圖像進行邏輯異或來構造零水印圖像。將零水印圖像送交第三方版權認證機構進行保管,當發生版權爭議時,通過算法恢復版權標識,達到版權保護的目的。實驗驗證算法對常見攻擊具有較好的魯棒性,能夠同時適用于矢量點、線、面數據,當數據量較小時,水印檢測效果也比較理想。很少很少有水印算法能抵御所有攻擊,同樣由于本文算法是基于格網劃分的,所以不能抵抗旋轉攻擊,這是本文算法的不足之處,將在今后的研究中著力解決。 目前,同時適用于矢量點、線、面數據的水印算法鮮有見到,同時利用矢量點、線、面3種數據特征來共同構造水印信息的相關算法還較少,這將是今后的研究重點。 [1] 李安波,閭國年,周衛.GIS矢量數字產品版權認證技術[M].北京: 科學出版社,2012: 1-5. [2] YAN Haowen,LI Jonathan,WEN Hong.A key points-based blind watermarking approach for vector geo-spatial data[J].Computers,Environment and Urban Systems.2011,35(6): 485-492. [3] 朱長青,許徳合,任娜,等.地理空間數據數字水印理論與方法[M].北京:科學出版社,2014 :1-10. [4] 許德合,朱長青,王奇勝.利用QIM的DFT矢量空間數據盲水印模型[J].武漢大學學報(信息科學版),2010,35(9): 1100-1103. [5] 馬桃林,顧翀,張良培.基于二維矢量數字地圖的水印算法研究[J].武漢大學學報(信息科學版),2006,31(9): 792-794. [6] 閔連權.一種穩健的矢量地圖數據的數字水印[J].測繪學報,2008,37(2): 262-267. [7] 王奇勝,朱長青,許德合.利用DFT相位的矢量地理空間數據水印方法[J].武漢大學學報(信息科學版),2011,36(5): 523-526. [8] WEN Quan,SUN Tan Feng,WANG Shu Xun.Concept and application of zero-watermark[J].Acta Electronica Sinica,2003,31( 2) : 214-216. [9] 孫鴻睿,朱建軍,尹鵬程,等.一種基于矢量地圖特征點和分塊的零水印算法[J].地理與地理信息科學,2012,28(4): 111-112. [10] 張佐理,孫樹森,汪亞明,等.二維矢量數字地圖的零水印算法[J].計算機工程與設計,2009,30(6): 1473-1475. [11] 曹劉娟,門朝光,孫建國.二維矢量地圖雙重零水印算法[J].哈爾濱工程大學學報,2011,32(3): 340-344. [12] 孫鴻睿,朱建軍,李光強,等.一種基于矢量地圖要素編碼的零水印算法[J].工程勘察,2012,40(9): 54-57. [13] 郭仁忠.空間分析[M].2版.北京: 高等教育出版社,2001: 77-92. [責任編輯:劉文霞] A zero-watermark algorithm for vector data based on distribution center LYU Wenqing1,2, ZHANG Liming1,2 (1.School of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China) Few zero-watermark algorithm can be applied to all type vector data for copyright protection. This paper proposes a zero-watermark algorithm for vector data based on distribution center. Firstly, the vector data is divided into grid. Secondly, the distance of each point to the arithmetic mean center in the grid is calculated and distance sequence is compared with the average distance. If the distance is greater than or equal to the average, the record is 1, otherwise 0. Then, the majority of the 0 and 1 is counted in the grid and 0 or 1 is recorded to generate characteristic of data. Finally, the XOR operation is done between the shuffled watermark image and the characteristic value, then the zero-watermark image is obtained. Experiments show that the algorithm can be applied to all type vector data, and also has good robustness to common attacks including translation, scaling, cropping, format transformation, random delete point and so on. vector spatial data; arithmetic mean center; zero-watermark; robustness 2016-09-26 國家自然基金資助項目(71563025);甘肅省自然科學基金資助項目(148RJZA041,148RJZA028) 呂文清(1992-),男,碩士研究生. 著錄:呂文清,張黎明.一種基于分布中心的矢量數據零水印算法[J].測繪工程,2017,26(8):50-53,61. 10.19349/j.cnki.issn1006-7949.2017.08.011 P208 A 1006-7949(2017)08-0050-04
2 零水印的檢測
3 實驗分析

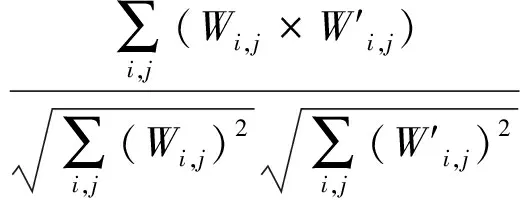

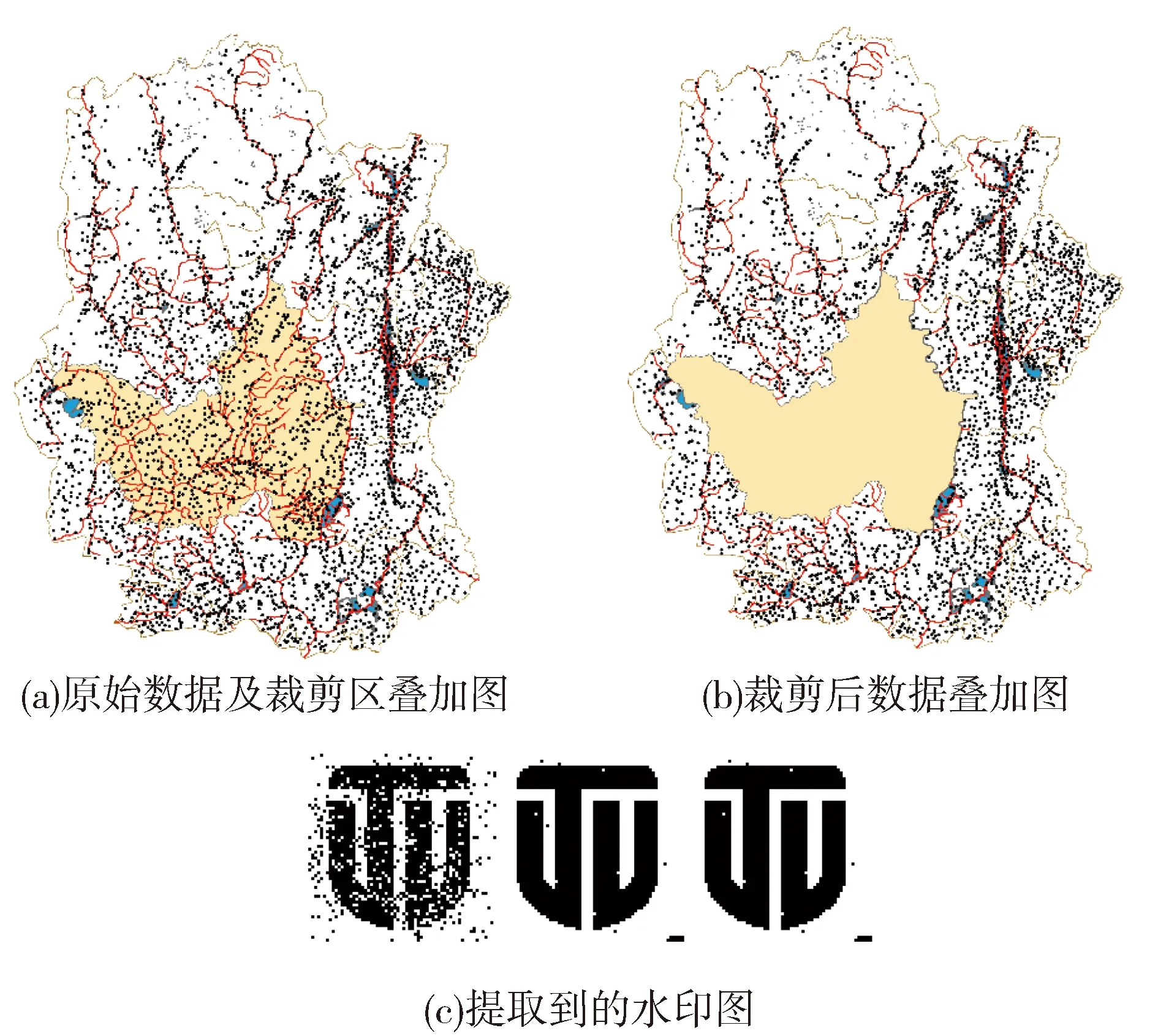
4 結束語

