基于故障樹的SIS可用性分析

徐飛，譚壯壯

(中國石油海洋集團工程有限公司，北京 100028)

基于故障樹的SIS可用性分析

徐飛，譚壯壯

(中國石油海洋集團工程有限公司，北京 100028)

安全失效概率(PFS)是衡量安全儀表系統(SIS)性能優劣的重要指標之一。在闡述SIS表決結構的設計特性及其可用性關系基礎上，研究了基于故障樹SIS表決結構的可用性關系，并通過具體實例進行驗證。研究結果表明： 表決結構故障樹可用性與設計特性不能完全相符，更加準確的可用性模型尚需進一步研究。

安全儀表系統 故障樹 可用性 安全失效概率 表決結構

安全儀表系統(SIS)已廣泛應用于石油、化工及冶金等行業中，是保障生產安全的重要措施，其安全性和可用性是衡量SIS性能優劣的兩大重要指標[1-2]。因安全性直接反應了SIS生產安全有效的防護能力，是設計SIS的前提條件，也是諸多學者研究的對象，但在實際應用中，人們希望SIS也具有一定的可用性，若系統可用性差，將使生產無法正常進行，從而造成巨大的經濟損失[3-4]。因此，對SIS進行可用性定量研究也有一定的意義。

安全失效概率(PFS)是可用性的具體量化指標，其定量計算模型主要通過可靠性框圖法、故障樹法和馬爾科夫(Markov)模型法三種方法建立[2-4]。在實際工程應用中，可靠性框圖計算簡單但是精確度不高；Markov模型雖然精確度高且能反應系統的動態性能，但當系統較大或系統狀態較多時，模型的建立和計算都會變的異常復雜；故障樹因模型計算量及精確度都較為均衡而在實際中應用較廣。

表決結構故障樹可用性模型在文獻[5]、文獻[6]中進行了主要描述，本文基于SIS表決結構設計特性的可用性關系，對文獻[5]、文獻[6]所述的故障樹可用性模型進行分析研究。

1 SIS表決結構設計特性可用性分析

SIS常見表決結構主要有“1oo1”，“1oo2”，“2oo2”，“2oo3”，其主要設計特性：“1oo1”結構是1個最小的系統，不具備容錯的能力，對設備的各種失效模式沒有保護能力，如果通道發生檢測到的安全失效或未檢測到的安全失效，系統就將發生安全失效；“1oo2”結構系統危險失效概率很低，但是安全失效概率卻增大了，任一通道的安全失效會造成系統的安全失效，容易造成受控系統的誤停車；“2oo2”結構將2個通道的輸出并聯，這樣可以保護單一通道的安全失效不致使系統的安全失效；“2oo3”結構中3個通道兩兩串聯構成“表決”電路，以確定當前系統的輸出[5]。

在實際應用中，“1oo1”表決結構安全性相對較低，“1oo2”表決結構適用于安全性很高的情況，但可用性差；“2oo2”表決結構適用于安全性要求一般，而可用性要求較高的情況；“2oo3”表決結構的安全性和可用性保持相對均衡，可用于安全性、可用性均較高的情況[7]。因此，從表決結構的設計特性可以得出，對于同一元件，幾種表決結構的可用性關系應該是PFS1oo2>PFS1oo1>PFS2oo3>PFS2oo2，即“2oo2”可用性最高，“2oo3”次之，“1oo1”較低，“1oo2”最低，但通過故障樹建立的SIS可用性模型并不能確定上述表決結構的可用性關系。

2 基于故障樹SIS可用性分析

2.1 SIS故障樹可用性模型

文獻[5]、文獻[6]通過故障樹建立了可用性模型，以“1oo1”為例進行簡要說明，“1oo1”結構系統安全失效的故障樹如圖1所示。

圖1 “1oo1”故障樹模型示意

如果通道發生檢測到的安全失效或未檢測到的安全失效，那么系統將發生安全失效。在通道的失效概率很低的情況下，系統安全失效概率PFS近似為

PFS1oo1=λSD×TS+λSU×TS

(1)

式中：λSD——可檢測的安全失效概率，λSD=λS×DC;λS——安全失效概率，λS=λ×(1-Q);λ——元件失效概率；Q——安全失效比率；DC——診斷覆蓋率；λSU——未檢測的安全失效概率，λSU=λS×(1-DC)；TS——停車后的重啟時間。

文獻[5]、文獻[6]利用上述方法分別得出“1oo2”,“2oo2”及“2oo3”可用性模型如下：

PFS1oo2=(λSUC+λSDC+2λSDN+2λSUN)×TS

(2)

PFS2oo2=λSUC×TS+λSDC×TS+

(λSDN×RT+λSUN×TI)2

(3)

PFS2oo3=3λSUC×TS+3λSDC×TS+

3(λSDN×RT+λSUN×TI)2

(4)

式中：λSUC——未檢測的共因安全失效概率，λSUC=λSU×β，β——共因失效因子；λSDN——可檢測的不共因安全失效概率，λSDN=λSD×(1-β)；λSDC——可檢測的共因安全失效概率，λSDC=λSD×β;λSUN——未檢測的不共因安全失效概率，λSUN=λSU×(1-β);TI——周期性功能測試間隔；RT——在線修復時間。

2.2 SIS可用性分析比較

通過故障樹模型[5-6]及相應PFS公式可以看出，“1oo1”與“1oo2”公式構成類似，而“2oo2”與“2oo3”公式構成類似，故分別進行分析比較。

1) “1oo1”與“1oo2”，“2oo2”與“2oo3”的可用性分析。

PFS1oo2-PFS1oo1=(λSDN+λSUN)×TS

(5)

PFS2oo3-PFS2oo2=2λSUC×TS+2λSDC×

TS+2(λSDN×RT+λSUN×TI)2

(6)

由上述分析可以得出，表決結構PFS關系分別是：PFS1oo2>PFS1oo1,PFS2oo3>PFS2oo2，與表決結構設計特性一致。

2) “1oo1”分別與“2oo2”和“2oo3”以及“1oo2”分別與“2oo2”和“2oo3”的可用性分析。文中以“1oo1”與“2oo2”為例進行可用性分析比較。

PFS1oo1-PFS2oo2=λSUN×(TS-λSUN×TI2)+

λSDN×(TS-λSDN×RT2-2×λSUN×TI×RT)

(7)

上述分析結果中TS和RT通常以小時為單位，數量級別不超過102，TI通常以年為單位，若以1a計，數量級別不超過104，λSDN主要受λ,DC,β,Q這4個變量參數影響，通常其數量級小于10-5，從而λSDN×RT2數量級小于10-1，2×λSUN×TI×RT數量級別約為101，因而TS-λSDN×RT2-2×λSUN×TI×RT結果通常為正值。另TI2的數量級別在107，當故障率λ取值在10-7級別時，TS-λSUN×TI2結果基本為正值；當故障率λ取值在10-5級別時，TS-λSUN×TI2結果往往為負值。綜合兩部分的計算結果，式(7)最后的正負關系不能確定，即“1oo1”與“2oo2”可用性關系也不能定論，這與表決結構設計特性不能完全相符。

同理可對“1oo1”與“2oo2”，“1oo2”與“2oo2”，“1oo2”與“2oo3”的可用性進行分析比較，通過研究表明： 因影響參數取值區間的變化，表決結構之間同樣存在上述可用性關系的不確定性，導致不能與表決結構設計特性完全相符。

3 SIS可用性實例分析

通過具體數據，對表決結構之間的可用性關系進行了驗證分析。由于PFS計算主要受7個參數影響，為了研究方便，影響因素只考慮參數的自相關性，暫不考慮參數之間的互相關性，利用Matlab軟件對PFS影響參數分析進行仿真，其參數取值均為常用范圍，見表1所列。故障樹模型λ對PFS的影響分析如圖2所示。

表1 SIS參數取值

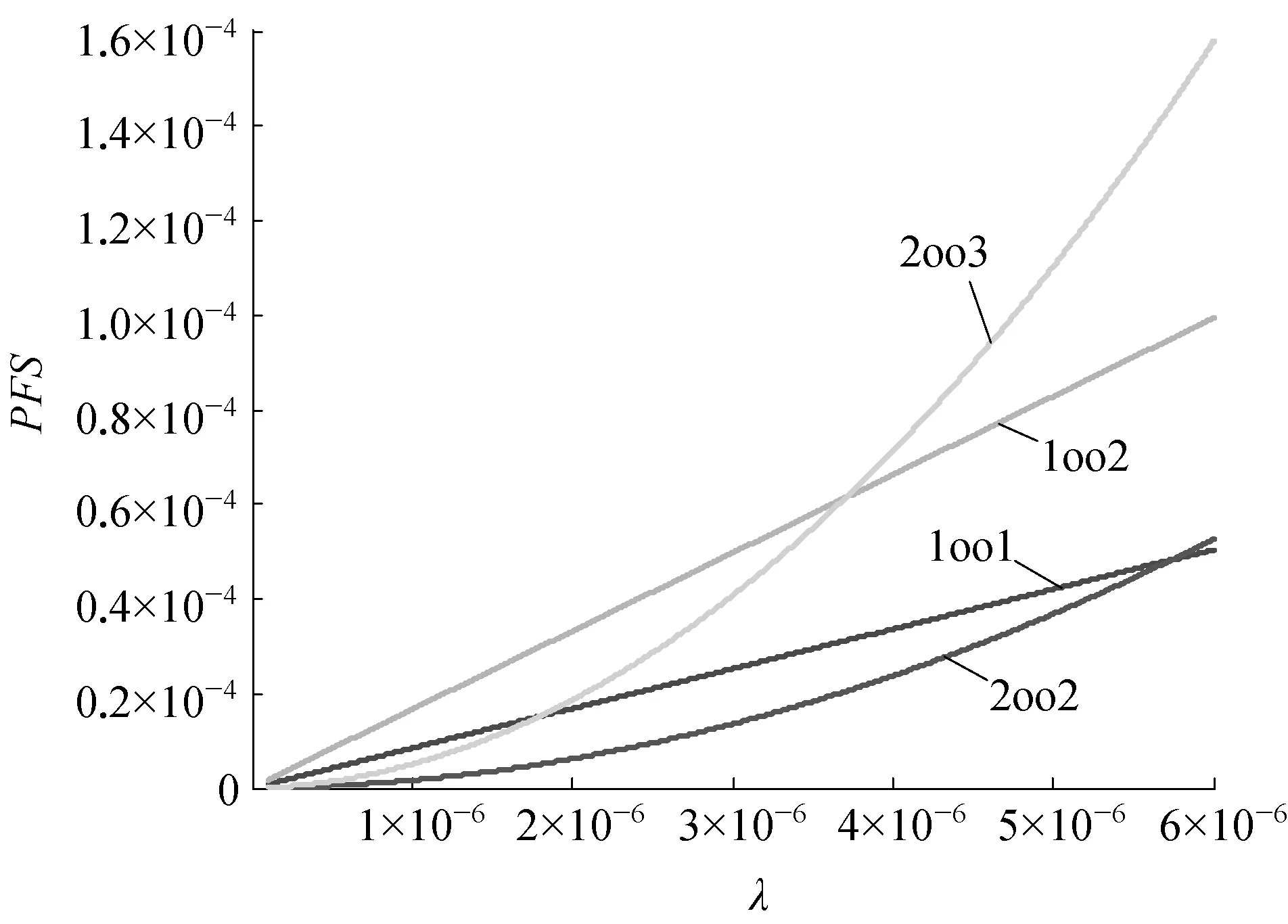
圖2 故障樹模型λ對PFS的影響分析示意

從圖2可清晰地看出，隨著λ的增大，其他因素不變的情況下，在不同λ取值區間內，四種表決結構PFS大小關系均有變化，即可用性關系存在不確定性。現選取具體的λ值，計算結果見表2所列，并最終分析得出可用性關系見表3所列。

表2 PFS計算結果

表3 表決結構可用性關系

根據圖1及表3的結果，“2oo3”與“1oo1”，“1oo2”以及“2oo2”與“1oo1”，“1oo2”之間的關系會因故障率λ的取值不一樣而出現變化，僅在λ取值較小的情況下，四種表決結構可用性關系與設計特性相符；但隨著λ取值增大，故障樹建立的模型不符合結構設計特性。

4 結束語

1) 基于故障樹的可用性模型，對于同一元器件，冗余結構“1oo1”與“1oo2”，“2oo2”與“2oo3”之間的可用性關系為PFS1oo2>PFS1oo1,PFS2oo3>PFS2oo2，與其設計特性相符；“1oo1”分別與“2oo2”和“2oo3”以及“1oo2”分別與“2oo2”和“2oo3”之間隨著影響參數取值不同，相互之間的可用性關系不能確定，與其設計特性不能完全吻合。

2) 基于故障樹的可用性模型在實際應用中具有一定的局限性，對于相關參數相對較小的場合，特別是λ取值較小時，計算模型可與設計特性可用性保持一致。

3) 基于故障樹的可用性模型與表決結構設計特性不完全符合的主要原因是由于參數TS和TI數量差別較大，而一般情況下TI是TS的數百倍，在式(1)，式(2)未考慮TI周期內的安全失效檢測，從而導致各表決結構可用性出現不同的關系。

4) 工作中，應充分考慮各參數在模型中的應用意義，如何確定更加準確的可用性模型尚需進一步研究。

[1] IEC. IEC 61508 Functional Safety of Electrical/Electronic/Programmable Electronic Safety — Related Systems[S]. IEC, 2010.

[2] IEC. IEC 61511 Functional Safety — Safety Instrumented Systems for the Process Industry Sector[S]. IEC, 2003.

[3] 王秉義，張惠良，左信.SIS安全聯鎖功能可用性分析[J].石油化工自動化，2012，48(01)： 13-17.

[4] 魏華.安全儀表的可靠性和可用性分析[J].石油化工自動化，2009，45(01)： 10-19.

[5] 陽憲惠，郭海濤.安全儀表系統的功能安全[M].北京： 清華大學出版社，2007.

[6] William M.Control Systems Safety Evaluation and Reliability[M]. USA： ISA, 1998： 335-419.

[7] 靳江紅，龐磊，趙壽堂，等.安全儀表系統的可用性分析及其定量評估[J].測控技術，2014，33(06)： 9-12.

Availability Analysis Based on Fault Tree for Safety Instrumented System

Xu Fei, Tan Zhuangzhuang

(China National Petroleum Offshore Engineering Co. Ltd., Beijing, 100028, China)

Probability of failing safety is one of important indicators to measure performance of safety instrumented system (SIS). Based on expounding of design characteristics and availability of SIS voting configurations, the availability of SIS voting configurations based on fault tree analysis (FTA) is studied. It is verified with some special actual cases. The results show the availability of SIS voting configurations is not completely consistent with design characteristics. More accurate availability model needs to be further studied.

safety instrumented system (SIS); fault tree analysis (FTA); probability of failing safety (PFS); voting configurations

徐飛(1984—)，男，安徽桐城人，2009年畢業于中國石油大學(北京)控制理論與控制工程專業，獲碩士學位，現就職于中國石油集團海洋工程有限公司，從事海上石油平臺儀表電氣設計工作，任工程師。

TP273

A

1007-7324(2017)03-0041-03

稿件收到日期： 2017-02-03，修改稿收到日期： 2017-03-14。