地震作用下連續剛構橋的受力分析
劉瑜(上海城建市政工程(集團)有限公司,上海200065)
地震作用下連續剛構橋的受力分析
劉瑜
(上海城建市政工程(集團)有限公司,上海200065)
連續剛構橋是大橋、特大橋梁的常見橋型,隨著新版《中國地震動參數區劃圖》的實施,對橋梁抗震提出了更高的要求。抗震設計貫穿橋梁設計全過程,準確進行地震模擬計算是抗震設計的保證。本文通過對某連續剛構橋梁施工過程的模擬以及成橋狀態下橋梁結構地震響應的分析,研究地震作用對于連續剛構橋梁受力分析的影響。
連續剛構施工過程有限元分析地震響應
1 工程概況
連續剛構橋梁位于安徽省某省級公路上,橋梁全長280m,跨徑布置為75+130+75m,屬于大型橋梁(見圖1)。橋梁分兩幅,單幅橋面寬度12m,單向三車道,橫斷面為單箱單室混凝土箱梁。上部結構采用連續剛構體系,跨中截面梁高3.6m,中支墩截面梁高8.0m,梁底采用二次拋物線變化。下部結構主墩采用雙肢薄壁墩,橋臺采用樁柱式臺,樁基礎。施工采用掛籃分節段懸臂施工工法,分為0#~19#共計20個節段,預應力鋼束分節段張拉。
2 有限元模型
有限單元法是將復雜問題分解為簡單問題求解的方法[2]。本工程采用工程設計中常用的MIDASCivil有限元軟件進行計算。工程經驗證明,該軟件模擬地震作用實用性較好。在有限元模型中,主梁,墩柱和樁基承臺等構件均采用一般桿系單元來模擬,邊跨梁端的邊界采用一般支撐模擬支座,樁基與土體之間的作用采用節點彈性支撐模擬,其節點剛度采用“m”法進行計算。
3 靜力計算
3.1 節段拼裝受力計算
本連續剛構橋梁采用節段懸臂施工,先施工下部樁基承臺和墩柱結構,澆筑0號塊,張拉預應力束,接著移動施工掛籃,澆筑1號節段,張拉預應力束,以此懸臂施工建立全橋模型,有限元計算模型如下圖2所示:
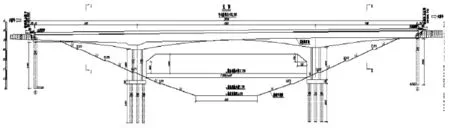
圖1 橋梁總體布置立面圖(單位:cm)

圖2 全橋有限元計算模型
在有限元模型中根據實際情況模擬具體的施工過程,由于本文篇幅限制,故只列出施工過程中受力最不利工況下,即最大懸臂狀態下結構的受力狀態。其中主梁內力如下表1所示:
最大懸臂狀態下,箱梁結構受力最不利位置出現在懸臂根部,其中最大主壓應力為10.9MPa,最大主拉應力為1.25MPa,均能滿足規范要求,故有限元模型計算是滿足要求的。在此基礎上提取橋墩的受力狀態,由于本橋結構和和荷載均為對稱結構,故只提取一個中墩的內力,其軸力,彎矩和剪力如下圖3所示:

表1 最大懸臂狀態下結構的內力(壓為負,拉為正)
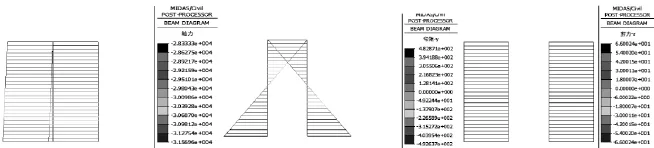
圖3 最大懸臂狀態下墩柱內力圖
從圖3可知,在施工過程中墩柱的剪力和彎矩均較小,墩柱受力以受壓為主,主要承受上部結構的恒載作用,其軸向壓力達到3.16×104kN,截面的最大壓應力為4.42MPa,在施工中應力有較高的安全儲備。
3.2 成橋狀態受力計算
在本橋的施工過程中,上部結構由懸臂狀態經過邊跨和中跨的合攏,變成連續鋼構橋梁,隨后在主梁施工鋪裝等二期恒載,達到成橋狀態。由于在施工中箱梁經過懸臂梁變連續梁這一體系轉換,結構在成橋階段的受力也隨之變化。列出成橋狀態下主梁的內力如表2所示:
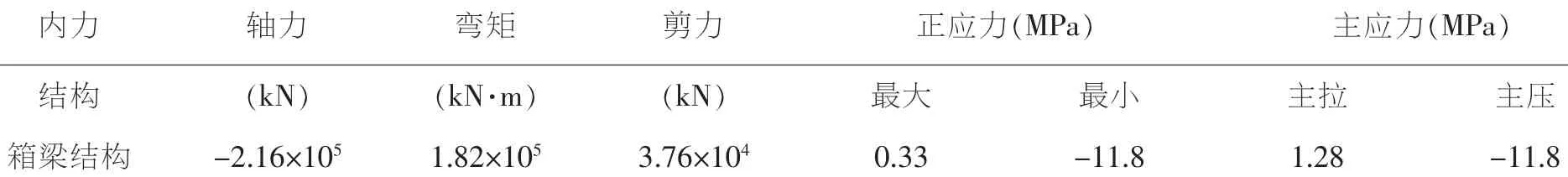
表2 成橋狀態下結構的內力(壓為負,拉為正)
成橋狀態下,箱梁結構受力最不利位置依然出現在懸臂根部,同時在跨中及邊跨合攏位置出現局部負彎矩區。主梁最大主壓應力為11.8MPa,最大主拉應力為1.28MPa,均能滿足規范要求。與最大懸臂狀態與成橋階段受力,成橋狀態下的彎矩增大了48%,同時在跨中及變化合攏段范圍內出現負彎矩區。但是應力指標并無明顯變化,且主梁應力分布更加均勻。同樣提取出此受力狀態下的橋墩的內力,以此作為后續抗震計算中橋墩的初始受力狀態,其內力圖如下圖4所示:
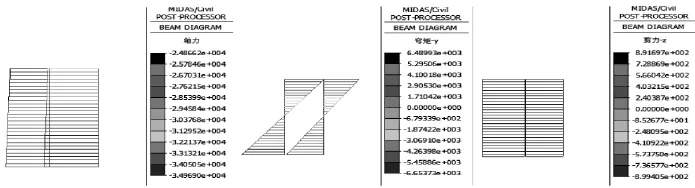
圖4 成橋狀態下墩柱內力圖(力:kN,彎矩:kN·m)
從圖4可知,在成橋狀態下墩柱的軸向壓力為3.50× 104kN,彎矩為6.65×103kN·m,剪力為899kN。相比施工階段,成橋狀態下墩柱的彎矩和剪力均有顯著的增大,從圖上可以看出,墩柱的正負最大彎矩在墩柱上下兩端,其反彎點約在1/2墩高處。上部恒載在成橋狀態的增量只是二期恒載和附屬等設施,軸向壓力變化不是很明顯,僅增大了11%,但橋墩結構依然以受壓為主。
4 抗震計算
4.1 地震設計參數
該橋梁結構抗震設計采用了二水準設防、二階段設計的抗震設計思想,第一水準相當于設計地震,第二水準相當于罕遇地震。地震動參數根據專門的《場地地震安全性評價報告》取值。根據該報告,橋址地區地震基本烈度為7度,區域地震動峰值加速度0.10g,地震動反應譜特征周期0.35s,結構阻尼比0.05,地震場地類型為II類。工程設計地震動加速度反應譜根據報告取值。采用多重Ritz向量法進行振型計算和動力分析。
4.2 動力特性分析
在抗震計算前,須先進行結構的動力計算,即特征值分析,為后續抗震計算提供橋梁結構的自振頻率等動力特性值。橋梁自振頻率能夠反映結構整體性能和受力體系特性,是反映橋梁剛度的最直接體現[3]。由結構動力學可知,結構的振動周期、頻率等動力特性與結構的質量和剛度分布有關。
在本文有限元模型中,主梁節點個數為110,考慮到X、Y、Z三個方向,模型的振型數達330多個,考慮到橋梁的振型中以低階為主,在本文計算中僅取前150階進行計算。其中橋梁的振型參與質量如下表3所示,由于篇幅限制,僅取前5階及后面每隔20階的振型參與質量。
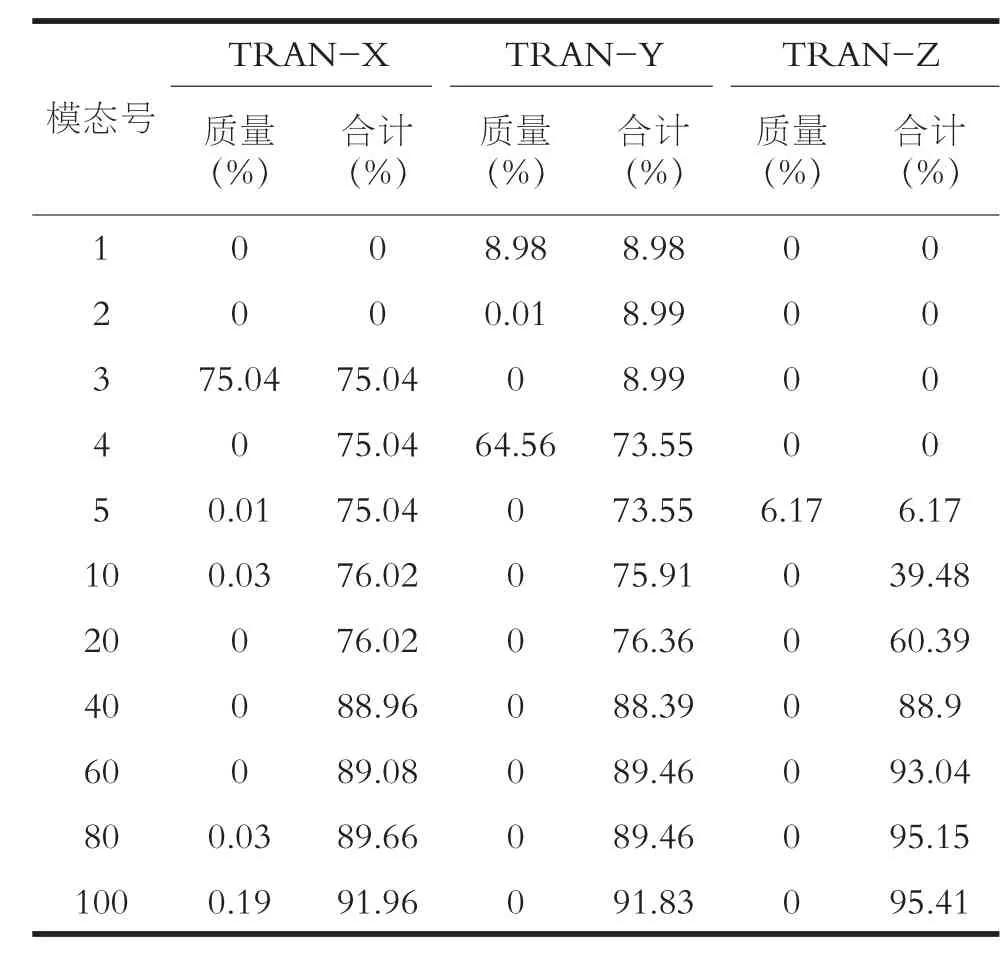
表3 振型參與質量
從上面表格可知,有限元模型在第100階時,運用里茲向量法求出的X平動、Y平動、Z平動三個方向的振型參與質量分別是91.96%、91.83%、95.41%,均超過了90%,滿足規范上振型參與質量達到總質量90%以上的要求。在此基礎上,提取有限元分析模型的前5階動力特性,特性值如表4所示:

表4 自振頻率和周期
從振型方向因子可知,振型1為橫橋向的第一階對稱振型,振型2為橫橋向的第一階反對稱振型,振型3為順橋向的第一階振型,振型4為橫橋向的第二階對稱振型,振型5為豎向的第一階對稱振型。
4.3 地震響應分析
地震作用是結構受迫振動的一種形式,結構在受迫振動時的響應與結構自由振動時的頻率和振動形式密切相關[1]。本節在動力分析模型的基礎上進行抗震設計,地震反應譜按照《公路橋梁抗震設計細則》中相關規定計算,由于本橋類型為B,故要同時驗算E1和E2地震作用下結構的響應。應保證在E1地震作用下,結構在彈性范圍內工作,基本不損傷,在E2地震作用下,延性構件(墩柱)可發生損傷,產生彈塑性變形,耗散地震能量,但延性構件(墩柱)的塑性鉸區域應具有足夠的塑性變形能力。
首先進行在E1地震、E2地震作用下的彈性計算,若E2彈性計算不滿足,則進行E2地震作用下的彈塑性驗算。按彈性計算得出的橋墩最大內力如下表5所示:
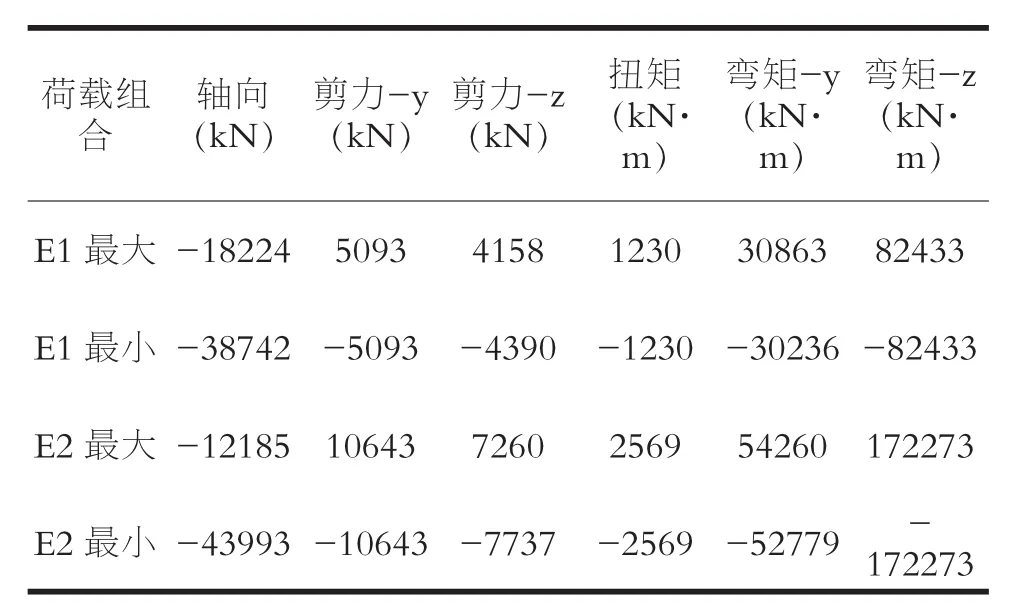
表5 地震工況下墩柱內力最大值
截面屈服彎矩與軸向受力有關,軸力壓力越大(壓力為負,拉力為正),屈服強度越小。為保守起見,取軸向壓力最大時的彎矩-曲率曲線為判斷截面是否屈服的標準,如圖5:
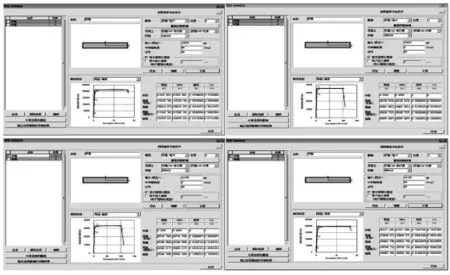
圖5 彎矩-曲率曲線
E1地震作用下,由圖5可知,在軸向受壓18224kN時,主墩截面順橋向屈服彎矩為35436kN·m,橫橋向屈服彎矩210306kN·m。從表5可知,主墩順橋向最大彎矩30863kN·m,橫橋向最大彎矩82433kN·m,均小于對應主墩截面兩個方向屈服彎矩。即可認為在E1地震作用下主墩處于彈性狀態,可以按照E1彈性狀態對墩柱進行強度驗算。
E2地震作用下,由圖5可知,在軸向受壓12185kN時,主墩截面順橋向屈服彎矩為32868kN·m,橫橋向屈服彎矩為195799kN·m。從表5可知,在E2地震作用下,主墩順橋向最大彎矩54260kN·m,橫橋向最大彎矩172273kN·m,順橋向最大彎矩大于主墩截面屈服強度,橫橋向最大彎矩小于主墩截面屈服強度,即順橋向部分單元進入彈塑性狀態,橫橋向可以滿足彈性狀態。因此,需要按照E2地震彈塑性狀態對墩柱進行強度驗算,同時對墩柱順橋向塑性鉸區進行抗剪驗算,對墩柱順橋向的塑性轉動進行變形驗算。
在有限元模型中,運用RC設計對橋梁墩柱進行抗震設計驗算可知,墩柱順橋向的最大正負彎矩位于橋墩墩底和墩頂處,且主墩墩底截面內力大于墩頂,即墩底受力更加不利,故在橋梁設計中應注意對薄弱部位的加強。
5 結語
(1)在有限元模型中模擬全橋施工階段,分析最不利施工階段和成橋階段主梁和墩柱受力,橋梁上下部結構的受力均滿足要求,為動力分析和抗震計算建立合理的初始受力狀態。
(2)在靜力分析的基礎上,進行動力分析即特征值分析,為抗震計算提供橋梁結構的自振頻率等動力特性值。
(3)抗震計算中,應注意橋梁的能力保護構件,如橋墩結構的受力是否進入彈塑性階段。本文有限元模型中,在E1地震作用下,橋墩處于彈性狀態,即可按彈性計算方法;在E2地震作用下,墩柱順橋向進入塑性狀態,應采用彈塑性驗算順橋向截面強度、塑性鉸區域抗剪強度和變形能力是否滿足規范要求。
(4)根據有限元計算結果可知,墩柱順橋向的最大正負彎矩位于橋墩墩底和墩頂處,即在塑性鉸區域,結構內力達到最大。因此在設計過程中應對橋梁的抗震薄弱處予以特別的重視,如對塑性鉸區域截面的加強,同時按照規范要求,采取相應的抗震隔震措施來確保橋梁結構在地震作用下的安全性。
[1]夏修,陳興沖,等.高墩大跨連續剛構橋抗震性能研究[J].西北地震學報,2010.01.
[2]陳星燁,顏東煌,等.某連續剛構梁橋的彈塑性抗震性能分析[J].中外公路,2008.03.
[3]范立礎.橋梁抗震[M].同濟大學出版社,1997.
[4]謝旭.橋梁結構地震響應分析與抗震設計[M].北京:人民交通出版社,2006.
[5]R.克拉夫.J.彭津著;王光遠譯.結構動力學[M].高等教育出版社,2006.11.
[6]李廉錕.結構力學(下冊)[M].北京:高等教育出版社,2010.
[7]CJJ 166-2011,城市橋梁抗震設計規范.住房和城鄉建設部.建筑工業出版社,2011.12.
[8]JTG/T B02-01-2008,公路橋梁抗震設計細則.北京:人民交通出版社,2008.08.

