簡諧運動的定量分析
——談一道競賽題的周期求解方法

許 龍 辛淑媛

(1.安徽省太和一中,安徽 阜陽 236600；2.安徽省太和中學,安徽 阜陽 236600)

·試題研究·

簡諧運動的定量分析
——談一道競賽題的周期求解方法

許 龍 辛淑媛

(1.安徽省太和一中,安徽 阜陽 236600；2.安徽省太和中學,安徽 阜陽 236600)

本文定量分析了兩種典型的簡諧運動，運用不同方法求解一道彈簧振子和單擺相結合的復合簡諧運動的周期，以期對中學生參加自主招生或物理競賽有所幫助.

簡諧運動；彈簧振子；單擺；周期

1 兩種簡諧運動

普通物理對簡諧運動有這樣的定義：質點在線性回復力的作用下圍繞平衡位置的運動叫做簡諧運動.常見的簡諧運動形式有兩種：彈簧振子和單擺.

1.1 彈簧振子

彈簧振子的簡諧運動是一種理想化模型，要求彈簧質量遠小于滑塊質量，無阻力和摩擦，滑塊被視為質點,以滑塊的平衡位置作為原點O，并建立坐標軸，x為坐標，等于其位移大小(如圖1).其回復力F與x成線性關系，即:F=-kx,其中k為勁度系數.

圖1

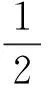
1.2 單擺

單擺的運動是將小球看作質點，在重力和懸線拉力的共同作用下在豎直平面內沿圓弧擺動，此時受到的合力F=mgsinθ，如圖2所示，在討論單擺做簡諧振動時，懸線與豎直位置的偏角θ很小，其位置與最低點的弧長近似于弦長x，即x=θl，其中l為單擺擺長。

圖2

2 彈簧和單擺復合運動

求解簡諧運動的周期在自主招生及中學物理競賽中經常遇到，也是學生感到比較困難的地方，下面筆者就一道自主招生的試題進行分析。

圖3

如圖3所示，有一彈簧擺，在擺長為l的單擺兩側各加一個勁度系數均為k0的輕質彈簧。設擺球靜止時兩彈簧均處于靜止狀態，求其小幅度振動的周期。

2.1 公式歸納法

這種解法較為巧妙，只要滿足F=-kx的條件，將相應的k帶入公式，即得物體簡諧運動的周期。這是求解振動周期最基本、最常用的方法，不過該解法一般只能應用于簡單的模型，局限性大。

2.2 機械能守恒法

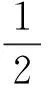
2.3 機械能對時間求導法

運用以上計算振動周期的方法都有一個前提：必須找出簡諧振動的回復力公式，則可得到振動周期甚至是運動學方程，在碰到類似題目時，學生可靈活選擇解題方法。

[1] 柯堯.賞析一道求振動周期的競賽題的多種解法[J].物理教師，2016，37(10)：92-93.

[2] 楊榕楠.更高更妙的物理[M].杭州：浙江大學出版社，2016：146-149.

[3] 漆安慎，杜嬋英.普通物理學力學[M].北京：高等教育出版社，2008：284-286.