含有粘彈性材料(橡膠)破口缺損圓盤的自由振動分析
謝坤+趙潔


摘 要:文章采用信號采樣與模態分析軟件,對切割后的含有粘彈性阻尼材料(橡膠)的厚圓盤的自由振動進行了試驗。為了分析試驗的精度,應用ANSYS分析軟件計算了整個破口厚圓盤的前30階模態(前六階為剛體模態),對試驗與有限元仿真結果進行了對比。
關鍵詞:破口缺損圓盤;自由振動;分析
中圖分類號:TB534+.3 文獻標志碼:A 文章編號:2095-2945(2017)19-0003-03
1 研究對象的具體參數
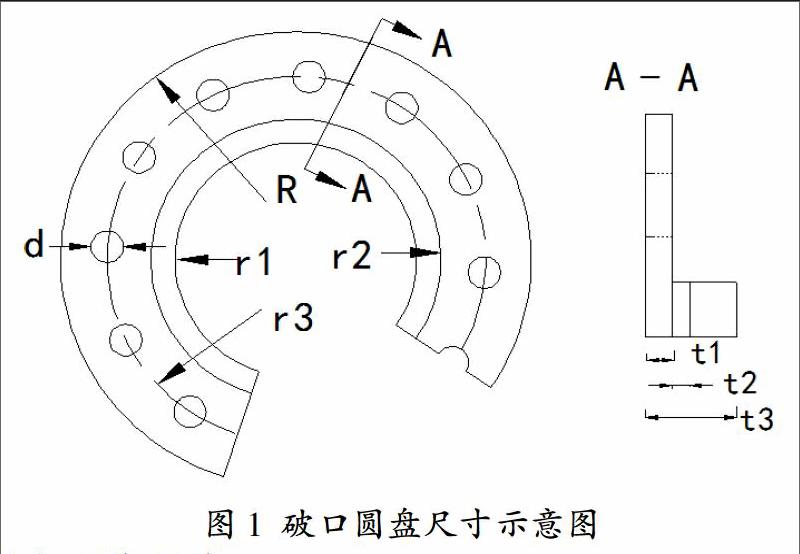
本報告的研究對象為破口的厚圓盤,在厚圓盤中包含了一層粘彈性的阻尼材料橡膠(剖面圖中厚度t2),厚圓盤的四周無約束。圓盤的幾何尺寸如下。
圖1幾何尺寸:R=194.05mm,d=26.70mm,r1=99.55mm,r2=119.55mm,r3=155.95mm,t1=11.2mm,t2=7.00mm,t3=37.8mm。
鋼材為Q235鋼,彈性模量E=2.06 e11 Pa,ρ=7800千克/立方米,泊松比v=0.3。
因為橡膠為超彈性材料,取橡膠的泊松比v為0.47, 取橡膠的密度ρ為1.35克/立方厘米。橡膠阻尼系數值我們取為0.4。
橡膠材料由于具有很好的粘性和彈性,在各行各業中運用廣泛,但橡膠變形的力學性能計算比較復雜,為幾何和物理的雙重非線性。在ANSYS的非線性有限元分析中,橡膠的本構關系采用兩參數的Mooney-Rivlin方程(W為橡膠材料的應變能密度函數,I為變形張量不變量):
2 試驗過程
2.1試驗儀器的設置與相關參數設定
試驗在船舶與海洋工程系結構力學實驗室進行,數據分析采用的是東昊公司的信號采樣與模態分析軟件。一共有36個測點,測點的分布見圖2。
2.2 相應的測量數據與分析
以四號和五號測點與例,測量得到兩個點的頻率-幅值響應曲線如圖3、圖4,可以看出在200Hz左右有一個峰值,因此,可以推斷結構的第一階頻率應該在200Hz左右。通常而言,只有結構前幾階模態具有較大的工程實際意義,因為較高的模態只有在結構經受沖擊或者爆炸載荷等劇烈響應時才會被激發出來,我們經過峰值搜索100-500之間的頻率搜索到三個峰值,分別是201.39Hz,397.22Hz,423.61Hz。
而從結構的動力響應來看,峰值較大的地方是在2000赫茲以上,這是因為我們在敲擊的時候是脈沖形式的沖擊載荷,因而在結構沖擊的過程中,結構的高頻響應被激發。通過有限元仿真計算,我們發現在30階模態之后,結構動力響應的頻率才能夠高于2000Hz,這也證實了我們的推斷,在沖擊載荷作用下,結構動力響應的頻譜非常豐富,而結構的高頻響應是占據主要的地位的。因此,如果僅僅計算結構固有自由振動的話,取前三階是合適的。
將模態參數文件導入結構文件,進行動畫顯示如下圖(圖5~圖8)。
從以上的圖中可以看出當每次敲擊后,遠離敲擊點振幅的衰減是非常快的,可見由于橡膠這種超彈性材料的存在,結構的對于能量的吸收是迅速而及時的。
由前面的分析可知,由于對于結構的施加的是沖擊載荷,激發了結構的高頻響應,我們同樣計算了4000Hz左右的響應,得到該階的頻率為4193.75Hz,從圖中可以看出,結構的不同節點的響應振幅大致趨于一致。
3 有限元數值仿真與分析
3.1 有限元數值仿真計算
本報告進行了有限元數值仿真研究,并與實驗結果進行了對比。應用ANSYS分析軟件,建模采用Soild45單元,將橡膠材料設定為超彈性,計算了整個破口厚圓盤自由振動的前30階模態(前六階為剛體模態)。
整個模型采用映射網格劃分,總共14522個節點,10722個單元。網格的劃分見圖9。
經過計算前30階的模態模態,現列出前15階模態如表1:
從表中可以看出1-6階為剛體模態,而7~9階的頻率相當接近,所以在試驗當中,我們只找出了一個峰值201.39Hz,而第10階模態可能也是由于與第7~9階非常接近,同時由于試驗儀器的分辨率有限的原因,因而也未分離出。下面的圖為第7,11和12階模態的變形云圖(圖10~圖12)。
3.2 數值仿真計算與試驗結果對比分析
將試驗結果與仿真結果對照得到誤差如表2:
4 結束語
本文對含有超彈性材料(橡膠)的破口圓盤的自由振動進行試驗與有限元數值計算研究,通過研究,超彈性材料(橡膠)對于外界激勵能量的吸收作用相當明顯,整個結構響應的衰減是非常迅速的,因此,橡膠等超彈性材料具有良好的減振吸聲作用。
由試驗值與數值計算值進行對比,誤差小于15%,尤其第一階誤差僅為2.45%,可見本文的試驗基本是正確的,數值計算結果是可信的。
試驗值與數值計算值進行對比發現,在190~210Hz間,響應頻率是非常集中的,這點是值得探討的。另外,在263.37處的理論計算值并沒有在試驗中分辨出,是有限元計算的參數設置問題,還是試驗本身的分辨能力問題,還有待探討。
參考文獻:
[1]ANSYS,Inc. Ansys Element Reference Guide10.0. Southpointe[Z].2005.
[2]楊曉翔.非線性橡膠材料的有限單元法[M].石油工業出版社,1999.
[3]成大先,等.機械設計手冊·常用工程材料分冊[M].化學工業出版社,2003.
[4](美)克拉夫(R.W.Clough),彭津(J.Penzien).結構動力學[M].科學出版社,1977.

