雙排非對稱四點接觸球轉盤軸承剛度分析

牛榮軍， 徐金超， 邵秀華， 鄧四二

(1.河南科技大學 機電工程學院, 河南 洛陽 471003; 2.空調設備及系統運行節能國家重點實驗室, 廣東 珠海 519000;3.洛陽鴻元軸承科技有限公司, 河南 洛陽 471132)

雙排非對稱四點接觸球轉盤軸承剛度分析

牛榮軍1,2， 徐金超1， 邵秀華3， 鄧四二1

(1.河南科技大學 機電工程學院, 河南 洛陽 471003; 2.空調設備及系統運行節能國家重點實驗室, 廣東 珠海 519000;3.洛陽鴻元軸承科技有限公司, 河南 洛陽 471132)

隨著軸承空間限制和高承載能力的目標要求，對傳統負游隙對稱型(初始接觸角α01=α02=45°)雙排四點接觸球轉盤軸承進行改進，提出負游隙非對稱型接觸角設計(α01為35°～60°，α02為90°-α01)，并基于赫茲接觸理論和滾動軸承設計方法建立負游隙非對稱雙排四點接觸軸承的力學模型。結果表明：隨著單向載荷軸向力Fa、徑向力Fr和傾覆力矩M增加，主剛度在開始階段基本呈下降趨勢，隨著單向載荷的增加非線性上升，負游隙的影響使得軸承的剛度變化曲線存在一個臨界拐點；初始階段隨著軸向負游隙量的增加，軸承的初始預緊剛度都得到明顯提高，但隨著載荷的增加負游隙對軸承剛度的影響逐漸減弱，最終基本趨于一致；單向載荷條件下，當軸向負游隙為-0.03 mm和非對稱接觸角取α01=55°，α02=35°時，其綜合軸承剛度最好；綜合外載工況下，負游隙取-0.03 mm和非對稱接觸角取α01=60°，α02=30°或α01=35°，α02=55°時軸承綜合剛性最佳。從提高軸承綜合剛性角度考慮，非對稱接觸角設計和負游隙都可以起到明顯效果。

機械學； 軸承； 非對稱接觸角； 負游隙； 四點接觸； 剛度

0 引言

轉盤軸承是一種廣泛應用于風力渦輪發電機、塔式起重機、炮臺、坦克等大尺寸的具有旋轉功能的機械中的軸承，四點接觸球轉盤軸承屬于轉盤軸承的一種。目前，四點接觸轉盤軸承普遍采用對稱接觸角設置，兩個接觸對初始接觸角都為45°[1-5]。隨著軸承空間限制和高承載能力的目標要求，采用非對稱接觸角和負游隙設計將會是其性能提升的有效解決方法[3-6]。因此開展非對稱接觸角和負游隙對此類大型轉盤軸承剛度的影響，進而合理地選取初始非對稱接觸角和游隙量，為新型非對稱雙排四點接觸球軸承的研發提供理論依據，極具現實意義。

關于滾動軸承的結構參數設計對軸承承載能力的影響，國內外學者已開展了較為深入的研究。文獻[1,4,7]系統研究了對稱接觸角條件下，軸承結構參數對轉盤軸承載荷分布和承載能力的影響。文獻[5-6]對負游隙單向載荷下轉盤軸承的剛度進行了研究。文獻[8]對深溝球軸承在奇壓和偶壓承載下的剛度進行了有限元求解，發現奇壓形式下的軸承剛度大于偶壓形式下軸承的的剛度。文獻[9-10]通過載荷、位移、剛度的關系對配對角接觸球軸承的剛度進行了分析。文獻[11]對角接觸球軸承進行了擬靜力學建模，在建模的基礎上對軸承的靜剛度和動剛度進行了求解。文獻[12]考慮油膜剛度對軸承剛度影響的情況下分析了溝曲率半徑系數、鋼球數量、軸向預緊量、外載荷等對雙列角接觸球軸承剛度的影響。Gunduz等[13]基于赫茲理論對背靠背、面對面雙列角接觸球軸承剛度進行了理論推導。Guo等[14]建立了考慮游隙在內的軸承有限元模型，對球軸承剛度矩陣進行推導，并進行試驗驗證。Sheng等[15]考慮轉速對球軸承剛度的影響，用隱函數微分法對球軸承的變剛度進行推導，發現轉速越高，軸承的剛度越低。Petersen等[16]給出了滾珠軸承的載荷分布和變剛度的解析表達式。

從上述研究可以看出，軸承準確的剛度計算具有重要意義。此外，目前對于軸承剛度的研究主要集中于中小型滾動軸承，而大型和超大型轉盤軸承的剛度計算涉及較少，并且還未見到非對稱接觸角雙排四點接觸球軸承相關承載能力研究的報道。本文首先基于赫茲(Hertz)接觸理論和滾動軸承設計方法建立非對稱負游隙雙排四點接觸球軸承的精確數學模型，并采用數值方法對力學平衡方程進行求解，然后分析單向和聯合載荷下，非對稱接觸角和游隙對軸承剛度的影響規律。為非對稱雙排四點接觸球軸承的初始接觸角和游隙的選取提供了理論參考依據，以輔助工程應用。

1 非對稱雙排四點接觸球軸承模型

圖1給出球位置角分布示意圖，dm為軸承的節圓直徑，j為鋼球的序號(j=1,2,3,…,z，z為鋼球的個數)，φj為第j個鋼球的位置角。

圖1 軸承滾動體位置角Fig.1 Position angle of rolling elements

圖2描述了非對稱雙排四點接觸球軸承的接觸角設置，α0m(m=1,2,3,4)表示軸承上下兩排4個接觸對的初始接觸角。其中，α01+α02=90°，α03+α04=90°，并取α01=α03.

圖2 軸承非對稱接觸角設置Fig.2 Asymmetric contact angle configuration of bearings

軸承外圈固定，內圈旋轉，軸承的曲率中心變化情況如圖3所示。取上排滾動體為研究對象，C1e、C2e表示受載前后外圈上下滾道的曲率中心，C1i、C2i表示受載前內圈上下滾道的曲率中心，C′1i、C′2i表示受載后內圈上下滾道的曲率中心。O表示受載前鋼球中心，O′表示受載后鋼球中心。α01、α02表示受載前接觸角，α1φ、α2φ表示受載后接觸角。

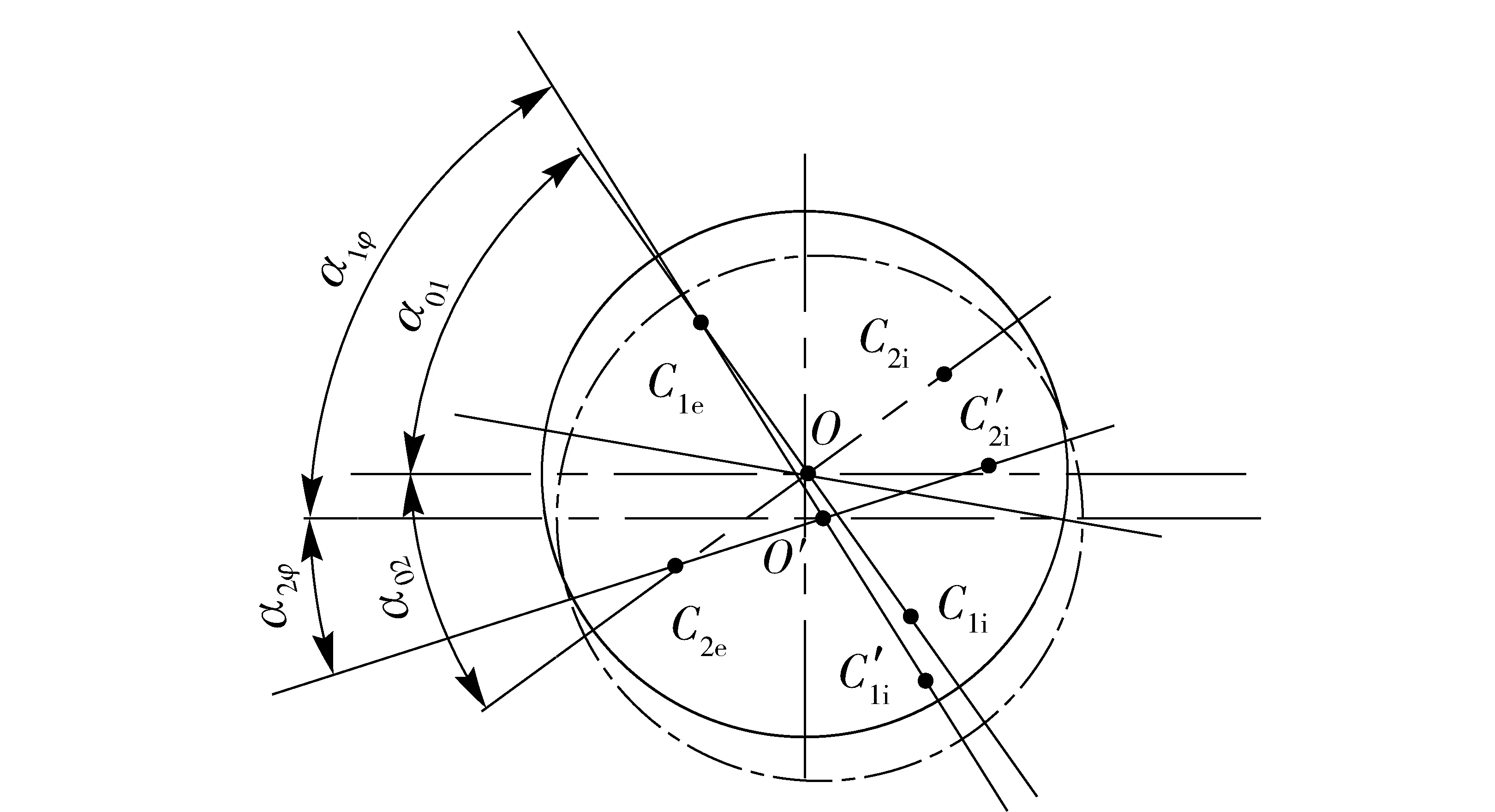
圖3 軸承的曲率中心及接觸角變化前后的位置Fig.3 Curvature center and contact angles of bearing before and after loading

圖4 軸承的受力圖Fig.4 Bearing forces equilibrium

由于轉盤軸承轉速很低，可以按照靜力學的方法來建立軸承整體力學模型，如圖4所示，其中，Fa、Fr分別為軸向力、徑向力，M為傾覆力矩，Q1φ、Q2φ、Q3φ、Q4φ為接觸對m在位置角φ處的法向接觸載荷，dc為雙排鋼球中心距。內圈相對外圈在外部載荷作用下產生軸向位移量δa，徑向位移量δr和傾斜角位移量θ. 設軸向位移引起的軸向變形為δa，徑向位移引起的徑向變形分量為δrcosφ，傾角位移引起的軸向變形分量為Riθcosφ(Ri為內圈溝曲率中心軌跡半徑)，傾角位移引起的徑向變形分量為0.5dcθcosφ. 內圈相對外圈位移減小的方向為正，位移增加的方向為負。接觸對位移的正負如表1所示。

表1 接觸對位移的正負影響關系Tab.1 Positive and negative influences of contact on displacement

由于軸承受載后內圈相對外圈有位移，所以接觸對m(m=1,2,3,4)在位置角φ處的溝心距Amφ將發生變化。軸承接觸對m受載前溝心距Am為

(1)

(2)

(3)

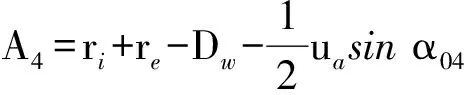
(4)

式中：ri為內溝道半徑;re為外溝道半徑;Dw為鋼球直徑;ua為軸向游隙(四點接觸球軸承一般取零游隙或負游隙[17]，本文取負游隙)。

受載后接觸對m在位置角φ處的溝心距Amφ為

A1φ=[(A1sinα01+δa+Ri1θcosφ)2+

(5)

A2φ=[(A2sinα02-δa-Ri2θcosφ)2+

(6)

A3φ=[(A3sinα03+δa+Ri3θcosφ)2+

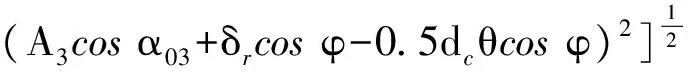
(7)

A4φ=[(A4sinα04-δa-Ri4θcosφ)2+

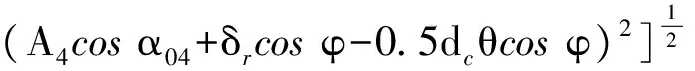
(8)

式中：Rim(m=1,2,3,4)表示內溝道曲率中心軌跡半徑。

(9)

(10)

(11)

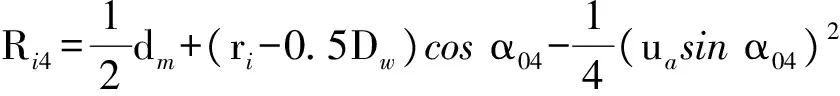
(12)

由于內圈相對于外圈發生相對位移，接觸對m在位置角φ處的接觸角也發生了改變，變化后的接觸角αmφ為

(13)

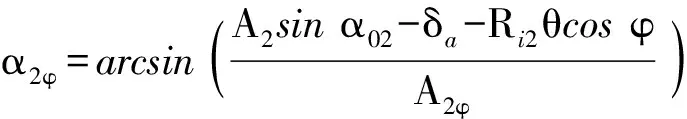
(14)

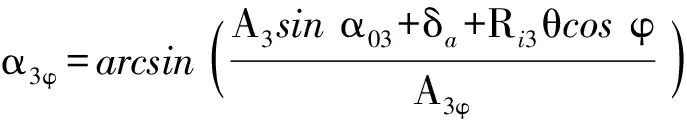
(15)

(16)

軸承受載后任意位置角φ處鋼球與內圈、外圈總的接觸變形δmφ等于位移后溝心距Amφ與受載前中心距Am之差，即

δmφ=Amφ-Am，m=1,2,3,4.

(17)

根據Hertz點接觸理論，接觸對m在位置角φ處的法向接觸載荷Qmφ與接觸變形δmφ的關系[18]為

(18)

式中：Knm表示滾動體與內圈、外圈之間總的負荷- 變形常數，對于軸承鋼制造的軸承，

(19)

式中：∑ρi表示鋼球與內滾道接觸點的主曲率和；∑ρe表示鋼球與外滾道接觸點的主曲率和；nδi表示鋼球與內滾道接觸點的主曲率函數F(ρ)相關的系數；nδe表示鋼球與外滾道接觸點的主曲率函數F(ρ)相關的系數；∑ρi、∑ρe、nδi和nδe的計算方法參照文獻[20]。

內圈在受到外部軸向載荷、徑向載荷、傾覆力矩以及鋼球對內圈的接觸載荷下處于平衡狀態，力學平衡方程為

Q4φsinα4φ)-Fa=0,

(20)

Q4φcosα4φ)cosφ-Fr=0,

(21)

Q3φcosα3φ-Q4φcosα4φ)cosφ-M=0.

(22)

(20)式～(22)式是三元非線性方程組，未知量是δa、δr、θ. 當給定軸向力、徑向力、傾覆力矩時，可以采用Newton-Raphson方法求解非線性方程組，根據求得的δa、δr、θ，進一步獲得軸承滾動體載荷和軸承剛度和軸承壽命等。

2 計算及結果分析

某1.5MW風力發電機變槳軸承，型號B033-40-1 900/P5，結構參數如表2所示。材料為42CrMo，運行時受到軸向力272 kN、徑向力100 kN、傾覆力矩1 700 kN·m，對其進行分析研究。

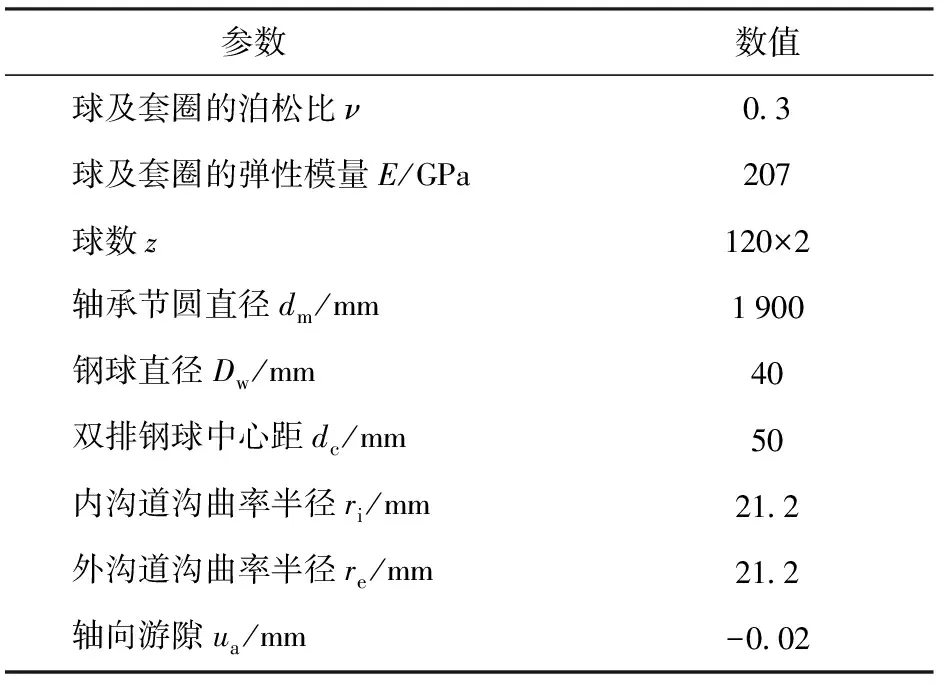
表2 雙排四點接觸轉盤軸承參數Tab.2 Parameters of double-row four-point-contact slewing bearing

軸承的剛度反映了其在承受負載時抵抗彈性變形的能力，是軸承結構對彈性變形難易程度的表征[19]。通過軸承載荷平衡方程對位移量求導，可以獲得非對稱雙排四點接觸球軸承的剛度矩陣。

本文用Kaa、Krr、Kθθ分別表示軸承的軸向主剛度、徑向主剛度、角主剛度，主剛度能判斷出軸承的結構和選型是否合理，對于軸承的選型具有重要的指導意義。把通過Newton-Raphson方法求解得到的δa、δr、θ分別代入軸承的剛度矩陣中即可精確求出軸承的主剛度Kaa、Krr、Kθθ.

圖5 單向載荷下非對稱接觸角對軸承主剛度變化影響Fig.5 Influence of asymmetric contact angle on main stiffness of bearing under unidirectional load

2.1 非對稱接觸角對軸承剛度的影響

圖5分別給出軸承在單向Fa、Fr、M載荷作用下和軸向游隙為-0.02 mm時，非對稱接觸角分別取35°、40°、45°、50°、55°、60°情況下軸承的主剛度Kaa、Krr、Kθθ變化情況。由圖5可以看出，非對稱接觸角變化對軸承主剛度產生非常明顯的影響，特別是軸向剛度Kaa和角剛度Kθθ；隨著單向載荷Fa、Fr和M的變化，主剛度在開始階段基本呈下降趨勢，但是隨著單向載荷的增加主剛度出現非線性上升。其主要原因是開始階段由于負游隙的影響使得軸承產生一定的預載荷，提高軸承剛性，但隨著載荷增加，負游隙的影響逐漸減弱，在變化曲線拐點處負游隙的影響降到最小，后續階段軸承剛性的變化主要是由于載荷的影響作用；對于3個主剛度而言，隨著接觸角的增加，軸向剛度Kaa不斷提高，徑向剛度Krr和角剛度Kθθ在非對稱接觸角為60°時最大，45°時最小。這是因為軸承在只受軸向力作用下，接觸角越大，接觸面積增加，抵抗變形的能力增大，剛度增加，而軸承只受徑向力或力矩作用時，在接觸角為45°時，軸承是對稱結構，此時軸承受到的載荷最小，接觸面積最小，相應的徑向剛度和角剛度最小。

單向載荷作用下，非對稱接觸角對軸承主剛度Kaa、Krr和Kθθ產生明顯影響，在非對稱接觸角為α01=60°，α02=30°時最大。此外，隨著非對稱接觸角的增大，負游隙對軸承剛度的影響減弱，特別是軸向剛度，在接觸角為60°時軸向剛度曲線趨近于直線，拐點消失。

2.2 負游隙對軸承剛度的影響

圖6分別給出軸承在單向Fa、Fr、M載荷作用下和非對稱接觸角為35°、45°、55°時，軸向負游隙分別取為-0.01 mm、-0.02 mm、-0.03 mm情況下軸承的主剛度Kaa、Krr、Kθθ的變化情況。從圖6可以看出，負游隙對軸承主剛度產生非常明顯的影響，隨著軸向負游隙量的增加，軸承的初始預緊軸向剛度Kaa、徑向剛度Krr和角剛度Kθθ都得到明顯提高，但隨著載荷的增加，負游隙對軸承剛度的影響逐漸減弱，最終基本趨于一致；對于軸向剛度Kaa，當軸向負游隙為-0.03 mm和非對稱接觸角取55°時，其綜合軸向剛度最好。此時，隨著軸向載荷的變化，其剛性變化比較平穩，沒有明顯的剛度下降拐點；對于徑向剛度Krr和角剛度Kθθ，當軸向負游隙為-0.03 mm和非對稱接觸角取45°時，其綜合剛度最好，此時徑向剛度的拐點對于徑向載荷達到150 kN，角剛度的拐點對于傾覆力矩達到180 kN·m.

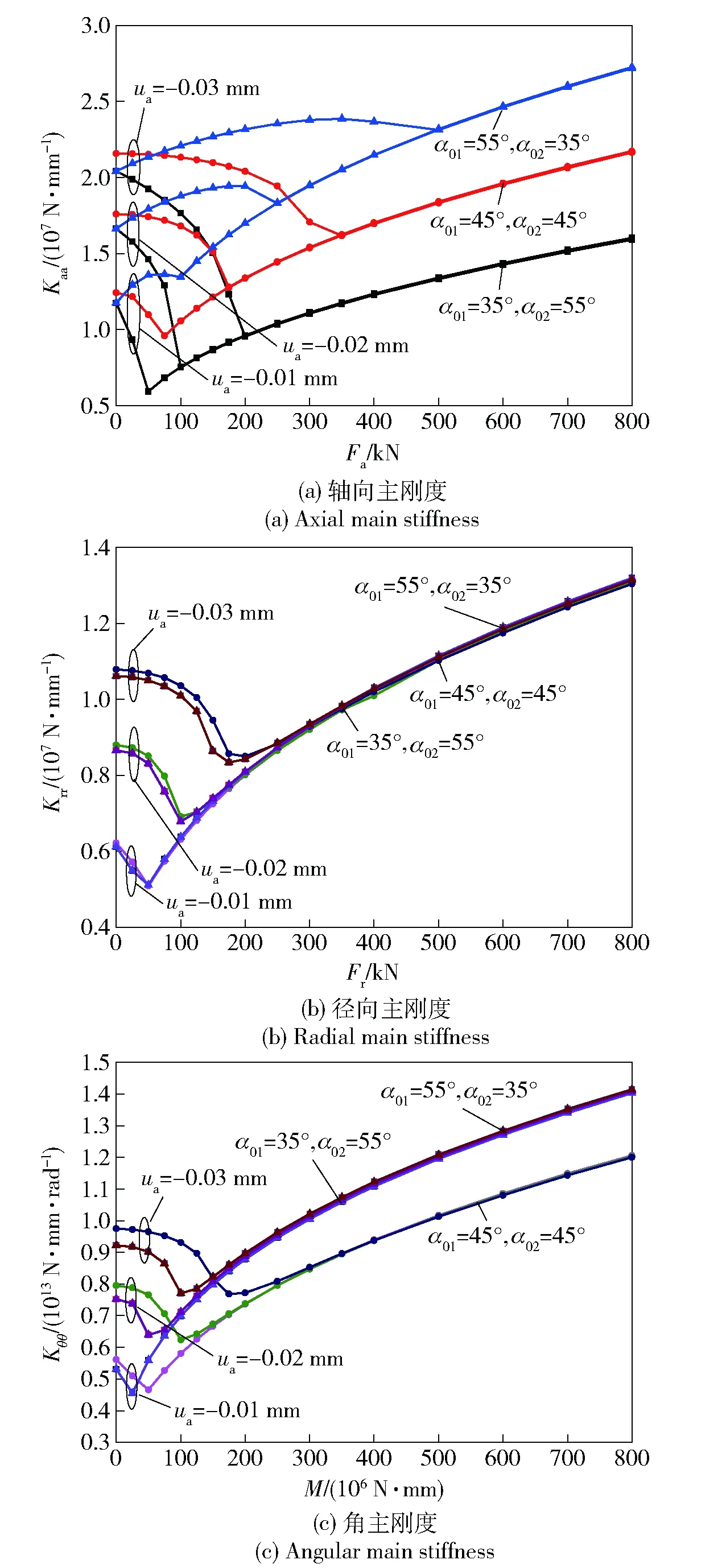
圖6 單向載荷下負游隙對軸承主剛度變化的影響Fig.6 Influence of negative clearance on main stiffness of bearing under unidirectional load

負游隙的大小可以明顯增強軸承的預緊剛性，改善軸承載荷分布均勻性，延長軸承壽命。但過大負游隙量會增加軸承滾道和滾動體載荷，軸承摩擦力矩增大，從而影響軸承的運轉靈活性和摩擦發熱，加速軸承潤滑脂性能退化，縮短軸承壽命。因此，通過初始負游隙預緊作用提高軸承剛性有個合適度問題，可以結合非對稱接觸角、滾動體直徑和數目等參數設計綜合提高軸承剛性。對于本研究對象，設計要求其軸向極限游隙為-0.03 mm. 從上述分析可以看出，單向載荷下，軸向剛度Kaa、徑向剛度Krr、角剛度Kθθ在負游隙為-0.03時最大。

2.3 聯合工況下軸承剛度分析

圖7給出在外載工況(軸向力272 kN、徑向力100 kN、傾覆力矩1 700 kN·m)，軸向游隙在-0.03～0.03 mm和非對稱接觸角在35°～60°時，軸承主剛度隨游隙和非對稱接觸角的變化曲線圖。

圖7 聯合載荷下負游隙和非對稱角對軸承剛度的影響Fig.7 Influences of negative clearance and asymmetric contact angle on bearing stiffness under combined load

由圖7可以明顯看出，在聯合載荷條件下軸承主剛度的變化明顯不同于單向載荷的影響，隨著軸承軸向游隙的增大，軸承軸向主剛度和徑向主剛度近似呈線性減小，而角剛度在非對稱接觸角為45°和50°時線性上升，其他非對稱接觸角情況呈線性下降趨勢；原軸承對稱接觸角設置(α01=α02=45°)，游隙變化對軸承軸向和角主剛度的影響不十分顯著，且隨著軸向游隙由負到正變化，角主剛度出現上升趨勢。綜合外載工況下軸向游隙取-0.03 mm和非對稱接觸角取α01=60°，α02=30°或α01=35°，α02=55°時軸承綜合剛性最佳。

隨著非對稱接觸角的變化，軸向剛度明顯高于徑向剛度，軸向剛度與角剛度變化趨勢相近，徑向剛度先下降后上升；非對稱接觸角為45°和50°時的主剛度明顯小于其他非對稱接觸角情況。這是因為在聯合負載下，接觸角為45°或50°時軸承受載較均勻，綜合Hertz接觸彈性變形量變大，剛度減小；在表2所示的聯合載荷和負游隙條件下，軸承輔剛度隨非對稱接觸角變化關系如表3所示，輔剛度?Fa/?δr與?Fr/?δa、?Fa/?θ與?M/?δa、?Fr/?θ與?M/?δr具有明顯的對稱性。從提高軸承綜合剛性的角度考慮，非對稱接觸角設計可以起到明顯效果。

表3 輔剛度隨非對稱接觸角變化Tab.3 Variation of auxiliary stiffness with asymmetric contact angle

因為變槳軸承受力情況復雜，這就要求軸承在單向載荷和綜合工況下都具有較高剛度。結合上述單向載荷下非對稱接觸角和負游隙對軸承剛性影響結論，對于本研究對象，可取負游隙ua=-0.03 mm和非對稱接觸角α01=60°，α02=30°作為軸承的設計參數。

3 計算結果驗證

文獻[20]給出了計算四點接觸球軸承主剛度的理論計算方法，將表2的軸承參數分別代入(23)式、(24)式、(25)式可計算得到雙排四點接觸球軸承在單向載荷和零游隙下的軸向、徑向與角度變形量。為更清晰描述軸承3個主剛性變化，分別改變軸向力Fa、徑向力Fr、傾覆力矩M值，記錄對應軸承的軸向、徑向和角位移量變化，并把理論計算與通過精確數值計算得出的結果進行比較驗證。

δa=δi,a+δo,a=

(23)

δr=δi,r+δo,r=

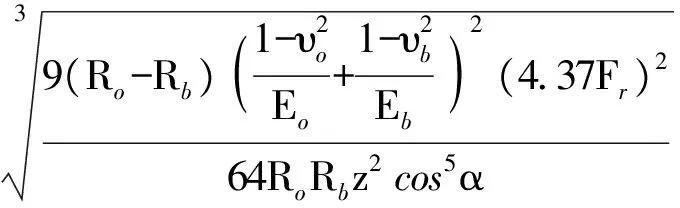
(24)

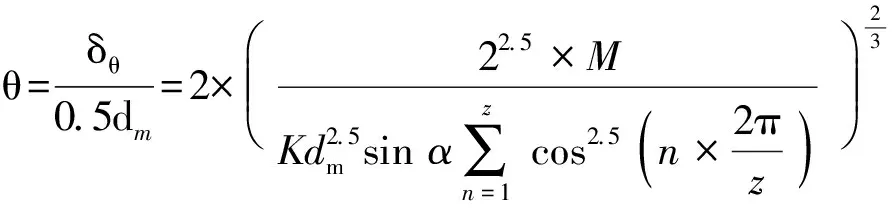
(25)

式中參數定義如表4.

為了驗證所求出剛性值的正確性，在測試原理如圖8所示的軸承剛性試驗臺上進行試驗測量，主要測試軸承分別在軸向、徑向和彎矩受力3種情況下的剛性值，并與數值和理論計算剛性值進行比對分析。由于軸承的尺寸較大，很難將其實際運轉并進行測量，本文以靜態施壓試驗方式來進行軸承軸向、徑向與彎矩的剛性測試。

表4 參數定義表Tab.4 Parameter definition list

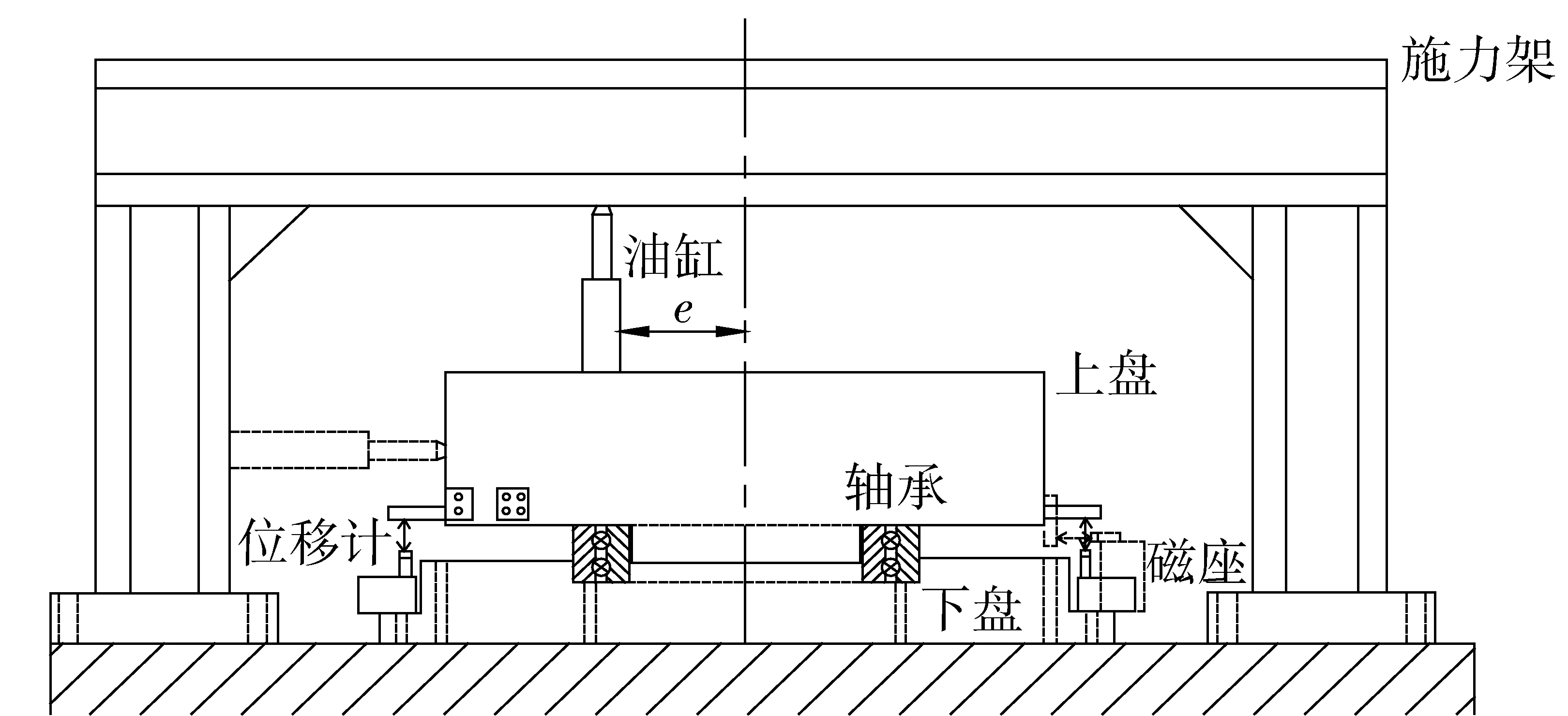
圖8 軸承剛性試驗原理圖Fig.8 Test principle diagram of bearing stiffness

進行彎矩剛性測量時，施加偏心力Fe到上盤，測量上盤的移動距離，求得上盤的旋轉角度。由于上盤的偏心加載力會造成上盤的軸向水平移動，因此分別安置兩支位移計于軸承測試平臺的180°方向，利用兩支位移計測量的位移彼此相消以消除軸向水平移動距離，其示意圖如圖9所示。由圖9可以得知兩支相180°方向的位移計測得的位移量分別為δa+δθ與δa-δθ，得到的位移量δθ再代入(25)式即可求得旋轉角度。

圖9 彎矩剛性試驗示意圖Fig.9 Test principle diagram of bending moment stiffness

圖10 非對稱雙排四點接觸球軸承剛性比較Fig.10 Stiffness comparison of asymmetric double-row four-point contact ball bearing

圖10給出非對稱接觸角分別為35°、45°、55°和軸向游隙為0時，理論計算與數值計算的軸向、徑向及角位移變化曲線圖，以及對稱接觸角設置(α01=α02=45°)時的試驗結果。有圖10可以看出：本文的計算結果與文獻[20]給出的理論計算結果相比，隨著外部單向載荷的增加，兩種計算結果的變化趨勢一致，位移變形量都呈非線性增加趨勢；在相同負載下數值和理論計算值都較試驗值小，其原因是軸承受到軸向、徑向和力矩負載時，由于Hertz接觸理論僅考慮滾動體與內外圈間接觸面受壓所產生的彈性變形，但實際上除了滾動體與與內外圈間的彈性變形量之外，還可能發生內外圈自身尺寸的改變，在徑向負載時尤其顯著，因而造成試驗值的變形量較理論值高。且Hertz接觸理論無法考慮到施力后滾動體與內外圈之間的相對運動和潤滑影響，從而也會影響到試驗結果。由文獻[18]與文獻[21]也可以發現，其軸承剛性試驗結果也同為理論值剛性較試驗值剛性高，即理論變形量小于試驗值的變形量，因此可以判斷在定性上試驗值會高于理論值，由圖10可以發現定性上試驗結果都符合這個現象；與數值計算結果和試驗結果相比，理論計算結果偏小，隨著單向載荷增加，二者偏離更加明顯。其主要原因是理論值沒有考慮軸承受載后滾動體與內外圈接觸角和負載區域的變化，從而影響軸承變形量計算結果的準確性，導致數值和試驗值均比理論值預估的更高。

在非對稱接觸角情況下，理論計算結果由于未考慮軸承受載后滾動體與內外圈接觸角和負載區域的變化，計算結果偏小，本文數值計算結果與試驗結果相近，說明本文提出的非對稱四點接觸球軸承計算模型的正確性和精確性，可以準確地用于此類轉盤軸承承載能力分析和壽命評估。

4 結論

1)單向載荷和負游隙條件下，非對稱接觸角對軸承主剛度產生明顯的影響，隨著單向載荷Fa、Fr和M增加，主剛度在開始階段基本呈下降趨勢，隨著單向載荷的增加主剛度出現非線性上升，剛度變化曲線存在一個臨界拐點，主要是由于負游隙的初始預緊作用。在非對稱接觸角為α01=60°,α02=30°時，Kaa、Krr和Kθθ最大。

2)軸承負游隙對軸承剛度產生明顯影響，隨著軸向負游隙量的增加，軸承的初始預緊剛度Kaa、Krr和Kθθ都得到明顯提高，但隨著載荷的增加，負游隙對軸承剛度的影響逐漸減弱。單向載荷條件下，當軸向負游隙為-0.03 mm和非對稱接觸角取α01=55°，α02=35°時，其軸承剛度最好。

3)從提高軸承綜合剛性角度考慮，非對稱接觸角和負游隙設計都可以起到明顯效果。綜合單向負載和聯合負載工況，游隙取-0.03 mm和非對稱接觸角取α01=60°，α02=30°時軸承綜合剛性最佳。

4)非對稱接觸角情況下，理論方法由于未考慮軸承受載后滾動體與內外圈接觸角和負載區域的變化，計算結果偏小，本文數值計算結果與試驗結果相近。

References)

[1] 王燕霜, 袁倩倩, 曹佳偉, 等. 特大型雙排四點接觸球軸承承載能力的研究[J]. 機械工程學報, 2014, 50(9):65-70. WANG Yan-shuang, YUAN Qian-qian, CAO Jia-wei, et al. Research on static load-carrying capacity of large size double row four-point contact ball bearings[J]. Journal of Mechanical Engineering, 2014, 50(9):65-70.(in Chinese)

[2] 芮曉明, 張穆勇, 黃浩然, 等. 雙排四點接觸球轉盤軸承載荷分布的研究[J]. 機械設計與制造, 2013(6):81-83. RUI Xiao-ming, ZHANG Mu-yong, HUANG Hao-ran, et al. Study of load distribution in a double-row four-point contact ball slewing bearing[J]. Machinery Design & Manufacture, 2013(6):81-83.(in Chinese)

[3] 陳龍, 趙聯春, 夏新濤, 等. 變槳軸承載荷分布分析[J]. 軸承, 2010(1):1-4. CHEN Long, ZHAO Lian-chun, XIA Xin-tao, et al. Load distribution for blade bearings[J]. Bearing, 2010(1):1-4.(in Chinese)

[4] 王燕霜, 袁倩倩. 負游隙對特大型雙排四點接觸球軸承載荷分布的影響[J]. 機械工程學報, 2012, 48(21):110-115. WANG Yan-shuang, YUAN Qian-qian. Influence of negative clearance on load distribution of large-size double row four-point-contact ball bearing[J]. Journal of Mechanical Engineering, 2012, 48(21):110-115.(in Chinese)

[5] 岳紀東, 李文超, 李建華，等. 負游隙四點接觸球軸承的剛度計算[J]. 軸承, 2014(4):20-22. YUE Ji-Dong, LI Wen-chao, LI Jian-hua, et al. The stiffness calculation of negative clearance of the four point contact ball bearing[J]. Bearing, 2014(4):20-22.(in Chinese)

[6] 王玉國, 宋吉祥, 王淼. YRT型轉臺軸承負游隙下的剛度分析計算[J]. 哈爾濱軸承, 2016, 37(1):8-10. WANG Yu-guo, SONG Ji-xiang,WANG Miao. Analysis and calculation for rigidity of YRT style turnable bearing with negative clearance[J]. Journal of Harbin Bearing, 2016, 37(1):8-10.(in Chinese)

[7] 李云峰, 姜迪. 千噸級全地面起重機用轉盤軸承的承載能力分析[J]. 機械工程學報, 2016, 52(1):109-114. LI Yun-feng, JIANG Di. Carrying capacity analysis of slewing bearing used in kiloton class whole ground crane[J]. Journal of Mechanical Engineering, 2016, 52(1):109-114.(in Chinese)

[8] 張宇, 謝里陽, 錢文學,等. 深溝球軸承的載荷分布與剛度特征研究[J]. 機械設計, 2012, 29(3):45-48. ZHANG Yu, XIE Li-yang, QIAN Wen-xue, et al. Study on load distribution and stiffness characteristics of deep groove ball bearings[J]. Journal of Machine Design, 2012,29(3):45-48. (in Chinese)

[9] 蔣蔚, 周彥偉, 梁波. 配對角接觸軸承剛度和摩擦力矩分析計算[J]. 軸承, 2006(8):1-3. JIANG Wei, ZHOU Yan-wei, LIANG Bo. Analysis and calculation of stiffness and friction moment of paired angular contact bearings[J]. Bearing, 2006(8):1-3.(in Chinese)

[10] 羅天宇, 羅繼偉. 角接觸球軸承預緊與剛度[J]. 軸承, 2015(6):1-4. LUO Tian-yu, LUO Ji-wei. Preload and stiffness of angular contact ball bearings[J]. Bearing, 2015(6):1-4.(in Chinese)

[11] 王東峰, 方斌, 李慶榮,等. 角接觸球軸承剛度計算與分析[J]. 軸承, 2016(4):1-5. WANG Dong-feng, FANG Bin, LI Qing-rong, et al. Calculation and analysis of stiffness of angular contact ball bearings[J]. Bearing, 2016(4):1-5.(in Chinese)

[12] 鄧四二, 董曉, 崔永存,等. 雙列角接觸球軸承動剛度特性分析[J]. 兵工學報, 2015, 36(6):1140-1146. DENG Si-er, DONG Xiao, CUI Yong-cun, et al. Analysis of dynamic stiffness characteristics of double-row angular contact ball bearings[J]. Acta Armamentarii, 2015, 36(6):1140-1146.(in Chinese)

[13] Gunduz A, Singh R. Stiffness matrix formulation for double row angular contact ball bearings: analytical development and validation[J]. Journal of Sound and Vibration, 2013, 332(22):5898-5916.

[14] Guo Y, Parker R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model[J]. Mechanism and Machine Theory, 2012, 51(5):32-45.

[15] Sheng X, Li B Z, Wu Z P, et al. Calculation of ball bearing speed-varying stiffness[J]. Mechanism and Machine Theory, 2014, 81(11):166-180.

[16] Petersen D, Howard C, Prime Z. Varying stiffness and load distributions in defective ball bearings: analytical formulation and application to defect size estimation[J]. Journal of Sound and Vibration, 2015, 337(17):284-300.

[17] 陳龍, 杜宏武, 武建柯, 等. 風力發電機用軸承簡述[J].軸承, 2008(12)：45-50． CHEN Long, DU Hong-wu, WU Jian-ke, et al. Summary of the bearing used in wind turbines[J]. Bearing, 2008(12):45-50.(in Chinese)

[18] Harris T A. Rolling beating analysis[M]. 5th ed. New York:John Wiley & Sons Inc, 2006.

[19] 鄧四二, 賈群義, 王燕霜. 滾動軸承設計原理[M]. 北京：中國標準出版社, 2009. DENG Si-er, JIA Qun-yi, WANG Yan-shuang. Rolling bearing design theory[M]. Beijing:China Standard Press,2009.(in Chinese)

[20] 吳伯彥. 大型軸承剛性鑒別及一般軸承剛性計算[D]. 臺灣:國立清華大學, 2008. WU Bo-yan. Identification of large bearing stiffness and rigidity calculation of general bearing[D]. Taiwan: National Tsinghua University, 2008. (in Chinese)

[21] Harris T, Rumbarger J H, Butterfield C P. Wind turbine design guideline DG03: yaw & pitch rolling bearing life[R]. Golden, CO, US: National Renewable Energy Laboratory, 2009.

Stiffness Analysis of Asymmetric Double-row Four-point-contactBall Slewing Bearing

NIU Rong-jun1,2， XU Jin-chao1， SHAO Xiu-hua3， DENG Si-er1

(1.School of Mechatronics Engineering, Henan University of Science and Technology, Luoyang 471003, Henan, China;2.SKL of Air-Conditioning Equipment and System Energy Conservation, Zhuhai 519000, Guangdong, China;3.Luoyang Hongyuan Bearing Technology Co．Ltd., Luoyang 471132,Henan, China)

Owing to the bearing space constraints and high load carrying capacity requirements, the traditional symmetric double-row four-point contact ball slewing bearing with negative clearance (α01=α02=45°)is improved, and a new asymmetric contact angle design(α01=35°-60°，α02=90°-α01) with negative clearance is proposed. A calculation model of double-row four-point-contact bearing with asymmetric contact angle is established based on the Hertz contact theory and rolling bearing design method. The influences of asymmetric contact angle and negative clearance on bearing stiffness are analyzed. The results show that,with the increase in unidirectional loadsFa,FrandM, the main stiffness decreases first and then increases nonlinearly, and a critical inflection point exists on bearing stiffness curve due to the negative clearance. In the initial stage, the initial preload stiffness of bearing is obviously improved, however, the effect of negative clearance on bearing stiffness is gradually weakened and eventually tend to be consistent with the increase in negative clearance. Under unidirectional loading condition, the integrated bearing stiffness is the best for the negative clearance being -0.03 mm andα01=55° andα02=35°. Under the combined loading condition, the bearing stiffness is optimum for the negative clearance being -0.03 mm andα01=60°,α02=30° orα01=35°,α02=55°. Asymmetric contact angle and negative clearance design have a significant effect to improve the overall stiffness of bearing.

mechanics； bearing; asymmertric contact angle； negative clearance； four-point-contact； stiffness

2017-01-06

國家科技攻關項目(JPPT-ZCGX1-1)；空調設備及系統運行節能國家重點實驗室開放基金項目(SKLACKF201603)；河南省自然科學基金項目(162300410086)

牛榮軍(1977—), 男, 副教授，碩士生導師。E-mail: niurongjun@163.com

TH133.33+1

A

1000-1093(2017)06-1239-10

10.3969/j.issn.1000-1093.2017.06.025