尺寸參數對橫向穩定桿側傾剛度的影響分析及驗證

王曉蓮，張學博

(中國第一汽車股份有限公司技術中心，吉林長春 130011)

尺寸參數對橫向穩定桿側傾剛度的影響分析及驗證

王曉蓮，張學博

(中國第一汽車股份有限公司技術中心，吉林長春 130011)

在橫向穩定桿開發設計過程中，尺寸參數的選擇直接影響橫向穩定桿的側傾剛度。穩定桿的側傾剛度受多個尺寸參數的影響，計算公式復雜，初始設計階段很難通過公式直觀判斷參數如何選擇。根據理論計算，繪制單一參數對橫向穩定桿側傾剛度的影響曲線，可直觀判斷不同參數對橫向穩定桿側傾剛度的影響程度。結合國內、外橫向穩定桿產品的實際尺寸參數，通過對比分析，驗證了繪制的尺寸參數影響曲線的正確性，解決了橫向穩定桿設計初期尺寸參數難以準確選擇和優化的問題。

橫向穩定桿；側傾剛度；尺寸參數；影響曲線

0 引言

橫向穩定桿是防止汽車在轉彎時發生過大的橫向側傾、保持汽車平衡的懸架系統重要零件，可提高車輛的操縱穩定性，提升舒適性和安全性[1-2]。在穩定桿設計過程中，各尺寸參數的選擇需要考慮對穩定桿側傾剛度的影響，同時根據整車布置空間進行調整。各尺寸參數對穩定桿側傾剛度的影響程度不盡相同，在穩定桿設計時需要綜合考慮。穩定桿側傾剛度計算公式非常復雜，設計初期很難通過公式直觀判斷尺寸參數如何選擇。文中通過繪制各尺寸參數對穩定桿側傾剛度的影響曲線，可以直觀地了解不同尺寸參數對穩定桿側傾剛度的影響幅度，能夠在穩定桿設計時準確、直觀、方便地進行尺寸參數選擇和優化。

1 直角形橫向穩定桿側傾剛度理論計算公式

直角形橫向穩定桿側傾剛度計算簡圖如圖1所示。

影響橫向穩定桿側傾剛度的基本尺寸參數為：L1、L2、L3、R、d。

圖1 直角形橫向穩定桿示意圖

直角形橫向穩定桿側傾剛度的計算公式[3-4]為：

(1)

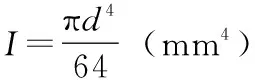
根據能量原理，推導出公式(1)中的P和U如下：

(2)

(3)

穩定桿基本尺寸參數如表1所示。

表1 穩定桿基本尺寸參數表 mm

根據公式(1)，繪制基本尺寸參數L1、L2、L3、R、d對橫向穩定桿側傾剛度的影響曲線。

2 基本尺寸參數

2.1 尺寸參數L1的影響曲線

保證穩定桿總長L不變，即L=1 000 mm不變。L1取點情況如表2所示。繪制尺寸參數L1對橫向穩定桿側傾剛度的影響曲線，如圖2所示。

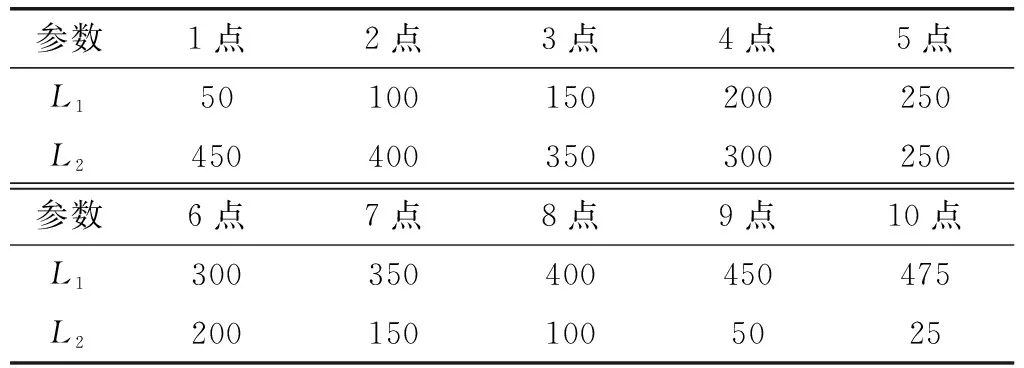
表2 L1取點表 mm

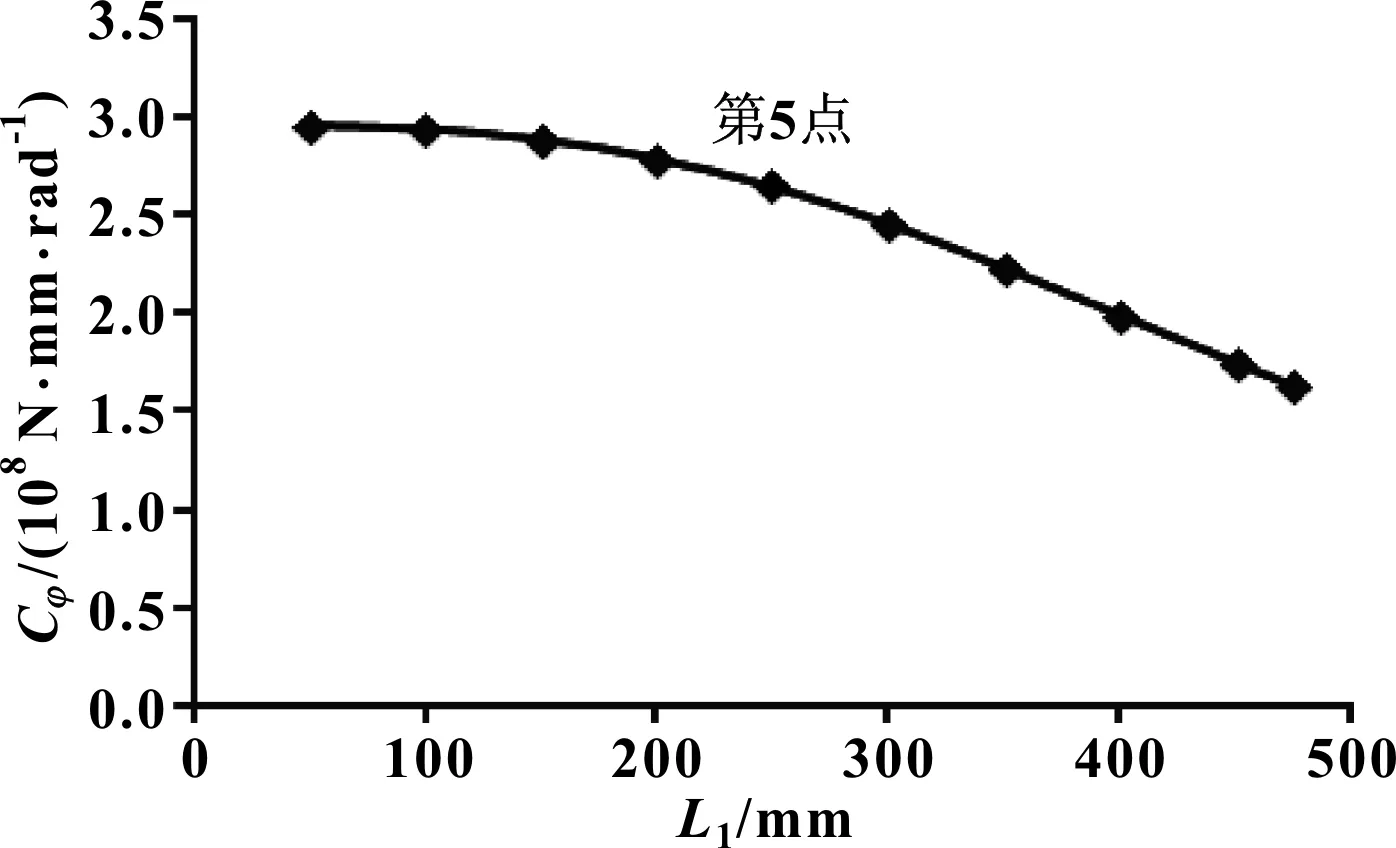
圖2 尺寸參數L1對穩定桿側傾剛度Cφ的影響曲線

分析圖2可知：尺寸參數L1從第1點變化至第4點，穩定桿側傾剛度降幅較平緩；第5點為影響曲線拐點，此時尺寸參數L1=L2=250 mm；L1從第5點變化至第10點，穩定桿側傾剛度降幅呈線性函數變化。

其他參數不變的情況下，L1越小，穩定桿側傾剛度越大。設計穩定桿時，需要考慮影響曲線的拐點(第5點)，即L1<250 mm時，尺寸參數L1的變化對穩定桿側傾剛度的影響較小。當空間布置緊張時，可充分利用L1影響曲線的拐點特性，調整整個穩定桿的設計方案。

2.2 尺寸參數L2的影響曲線

在其他參數不變的情況下，L2取點情況如表3所示。繪制尺寸參數L2對橫向穩定桿側傾剛度的影響曲線，如圖3所示。

表3 L2取點表 mm

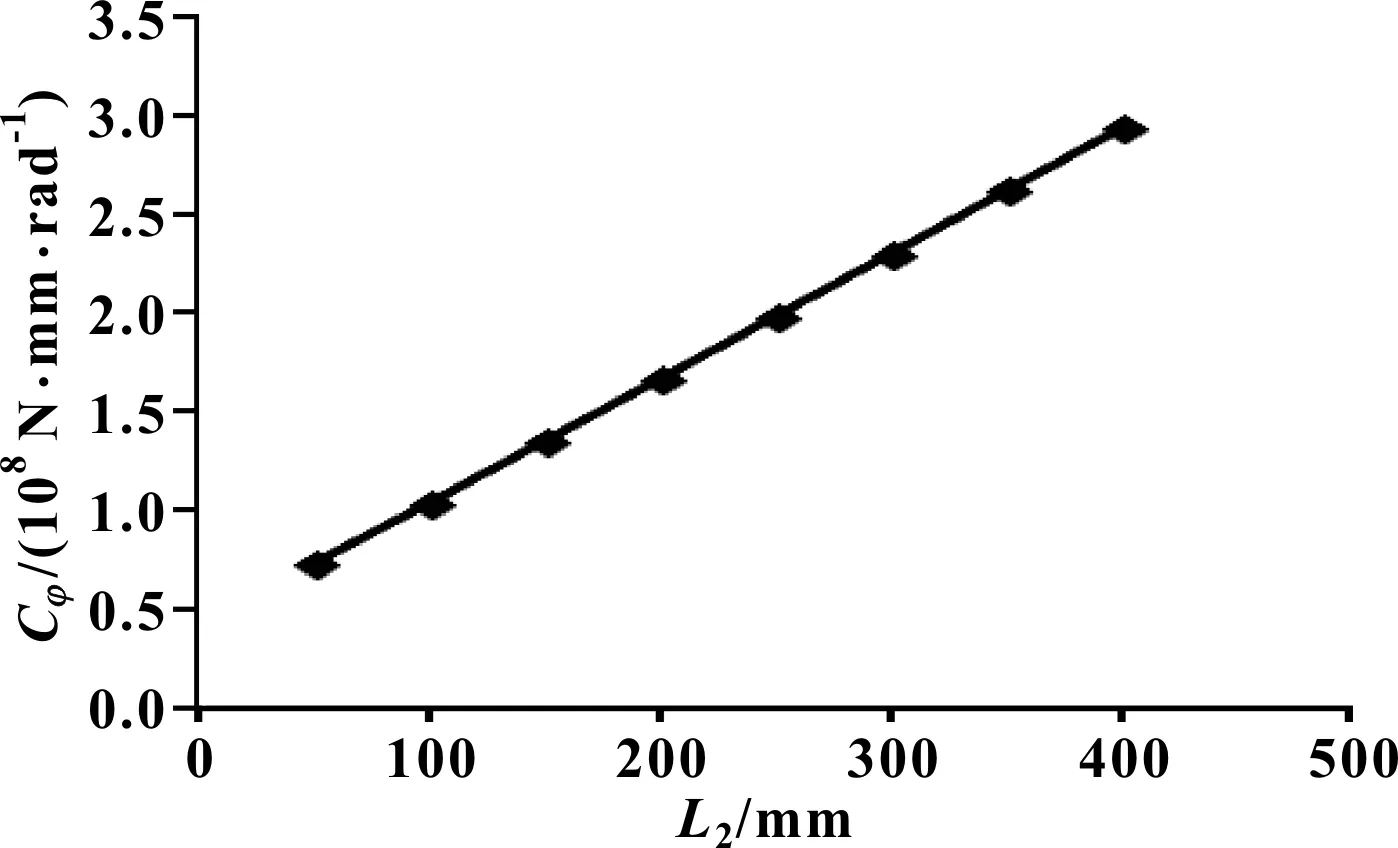
圖3 尺寸參數L2對穩定桿側傾剛度Cφ的影響曲線

分析圖3可知：其他參數不變的情況下，橫向穩定桿側傾剛度Cφ與尺寸參數L2呈線性函數關系，L2變大，穩定桿側傾剛度Cφ隨之變大。在布置空間允許的情況下，可適當加大L2的尺寸，獲取更優的穩定桿側傾剛度。

2.3 尺寸參數L3的影響曲線

在其他參數不變的情況下，L3取點情況如表4所示。繪制尺寸參數L3對橫向穩定桿側傾剛度的影響曲線，如圖4所示。

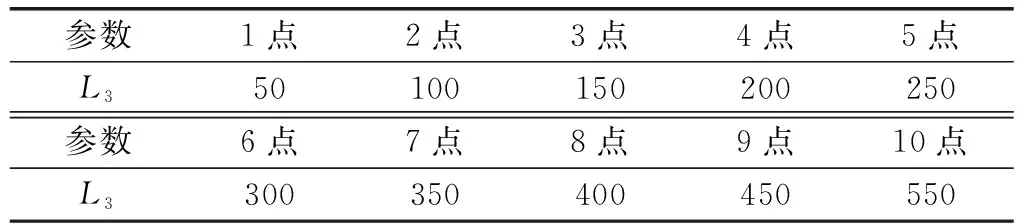
表4 L3取點表 mm

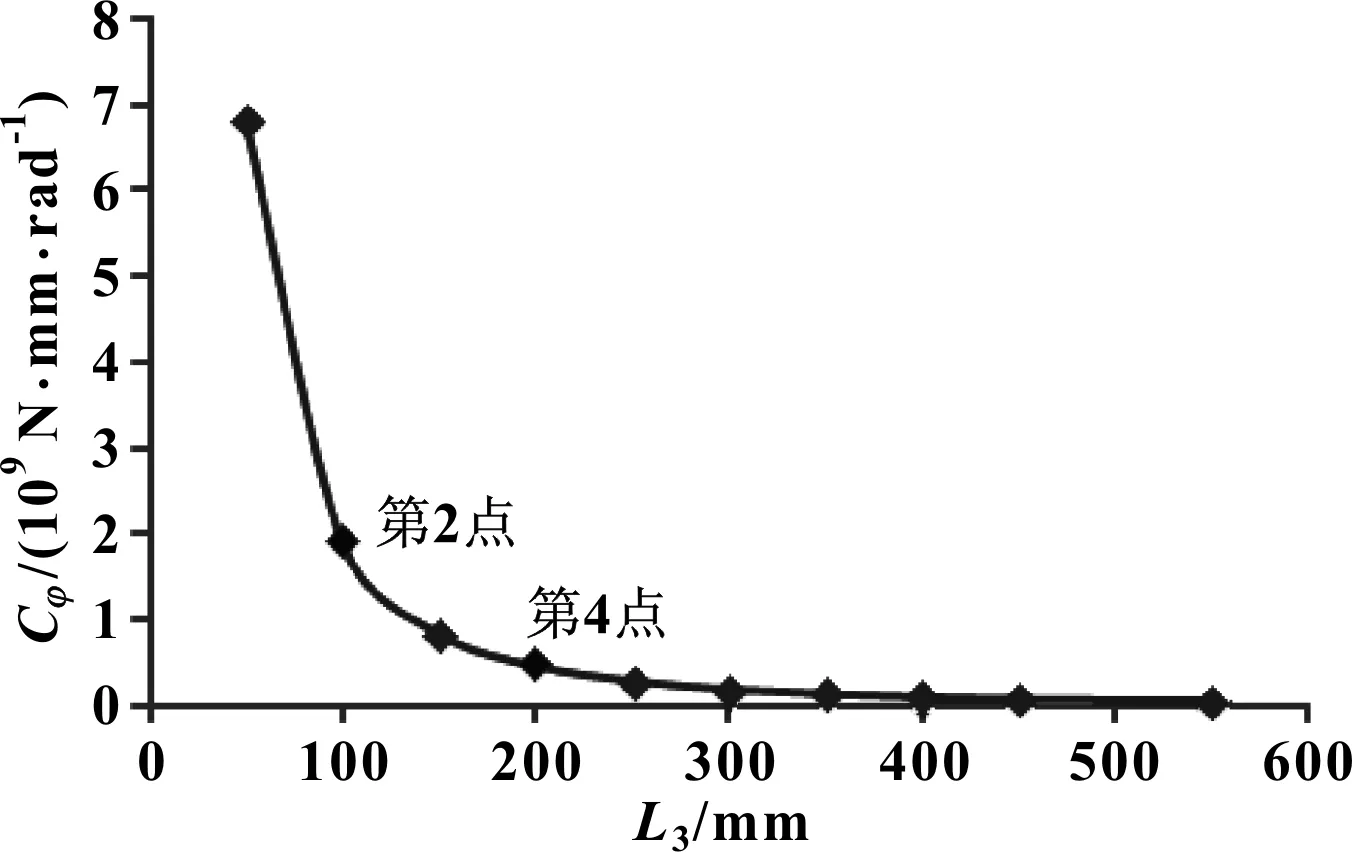
圖4 尺寸參數L3對穩定桿側傾剛度Cφ的影響曲線

分析圖4可知：尺寸參數L3從第1點變化至第2點，穩定桿側傾剛度降幅劇烈，降幅比例達到72.1%；第2點和第4點為影響曲線的兩個拐點；L3從第4點變化至第10點，穩定桿側傾剛度呈類似線性函數關系，降幅趨于平緩。

其他參數不變的情況下，L3越小，橫向穩定桿側傾剛度越大。設計穩定桿時，需要充分考慮尺寸參數L3的兩個拐點(第2點和第4點)。當L3<100 mm時，能夠獲得較高的橫向穩定桿側傾剛度，此時需綜合考慮空間布置和其他因素的影響；當L3>200 mm時，尺寸參數L3對橫向穩定桿側傾剛度的影響幅度逐漸減小。一般情況下，盡可能不要選擇過大的L3，以免對穩定桿側傾剛度造成不良影響。

2.4 尺寸參數R的影響曲線

在其他參數不變的情況下，R取點情況如表5所示。繪制尺寸參數R對橫向穩定桿側傾剛度的影響曲線，如圖5所示。

表5 R取點表 mm

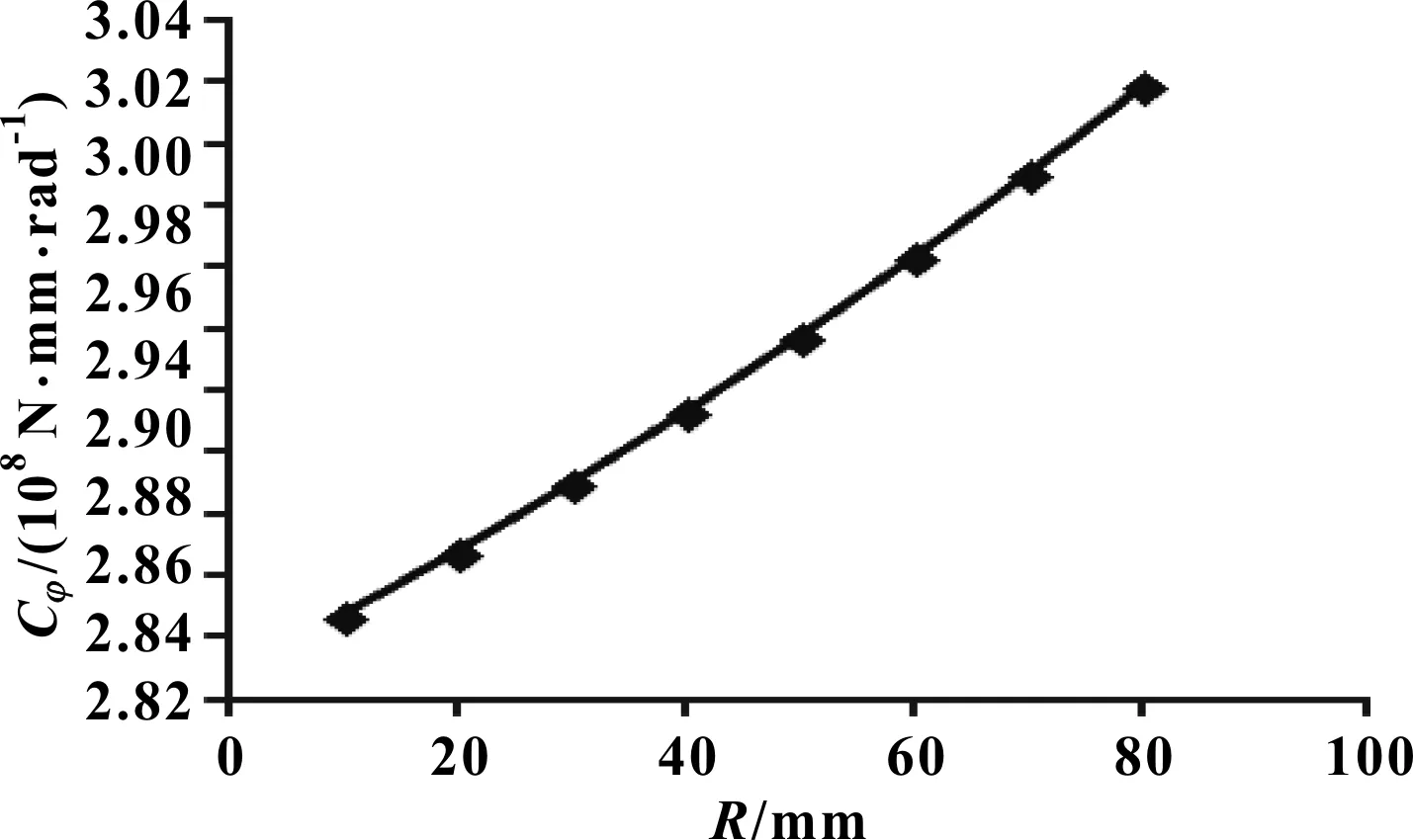
圖5 尺寸參數R對穩定桿側傾剛度Cφ的影響曲線

分析圖5可知：其他參數不變的情況下，橫向穩定桿側傾剛度Cφ與尺寸參數R呈線性函數關系，R變大，穩定桿側傾剛度Cφ隨之變大。從圖5還可以看出：尺寸參數R對穩定桿側傾剛度的影響曲線的斜率為629 943 N·mm/(rad·mm)。條件允許情況下，可適當加大穩定桿折彎半徑R，以獲取更優的側傾剛度。

2.5 尺寸參數d的影響曲線

在其他參數不變的情況下，d取點情況如表6所示。繪制尺寸參數d對橫向穩定桿側傾剛度的影響曲線，如圖6所示。

表6 d取點表 mm

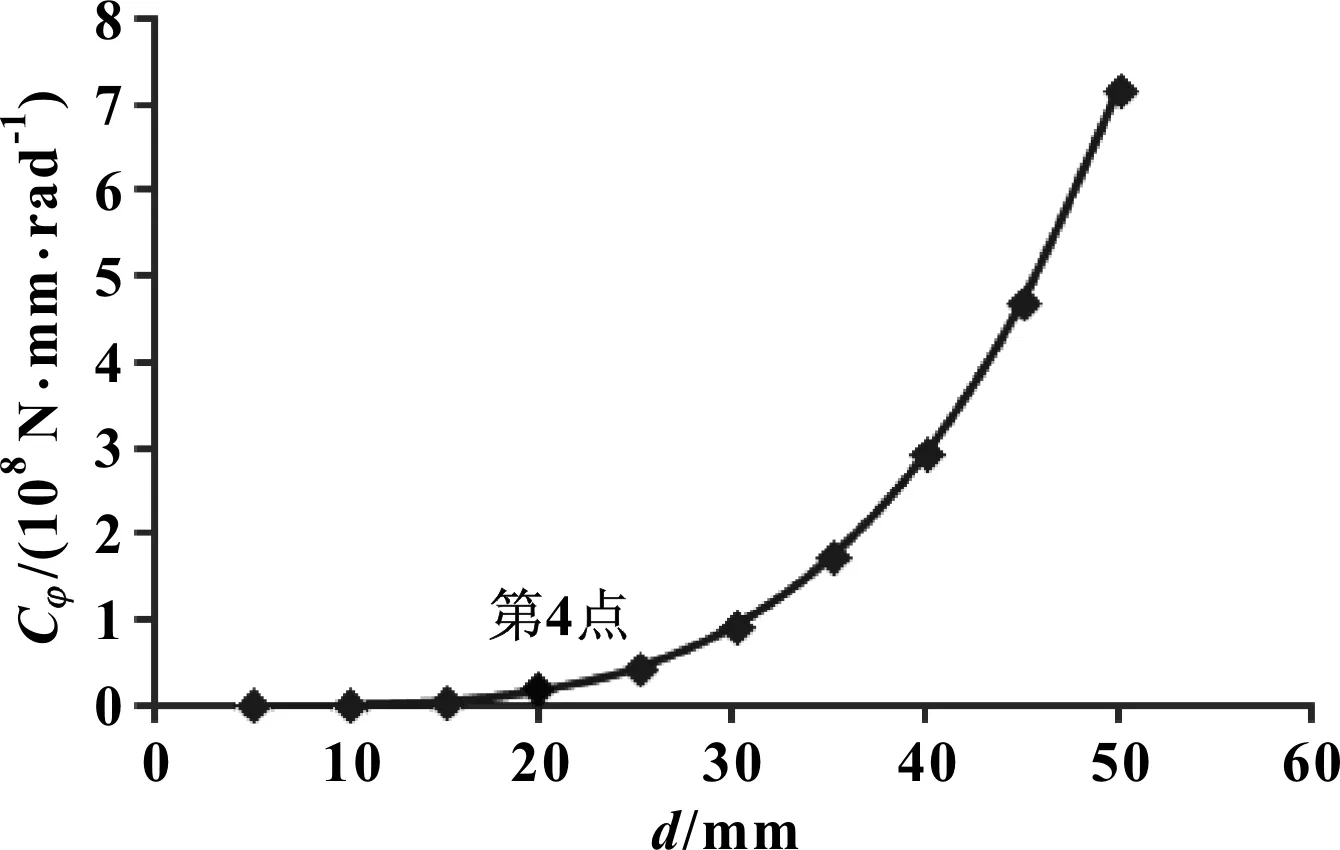
圖6 尺寸參數d對穩定桿側傾剛度Cφ的影響曲線

分析圖6可知：尺寸參數d從第1點變化至第4點，穩定桿側傾剛度變化幅度較平緩；第4點為影響曲線的拐點，從第4點開始，穩定桿側剛度隨尺寸參數d的變化幅度逐漸劇烈，曲線呈冪函數趨勢變化，與公式(1)相符合。在設計穩定桿時，可適當加大穩定桿外徑d的尺寸，獲取更優的穩定桿側傾剛度，同時，需要綜合考慮輕量化的需求。

3 截面尺寸參數

3.1 空心穩定桿外徑d′的影響曲線

隨著整車及零部件輕量化的需求不斷發展，市場上出現越來越多的空心橫向穩定桿。除了能夠降質量，實現輕量化的目標，選擇得當，空心穩定桿還能夠得到比實心穩定桿更優的側傾剛度，在設計上實現雙贏。

在其他參數不變的情況下，取內徑D=φ20 mm，保持不變。空心穩定桿外徑d′的取點情況如表7所示。繪制空心穩定桿外徑d′對橫向穩定桿側傾剛度的影響曲線，如圖7所示。

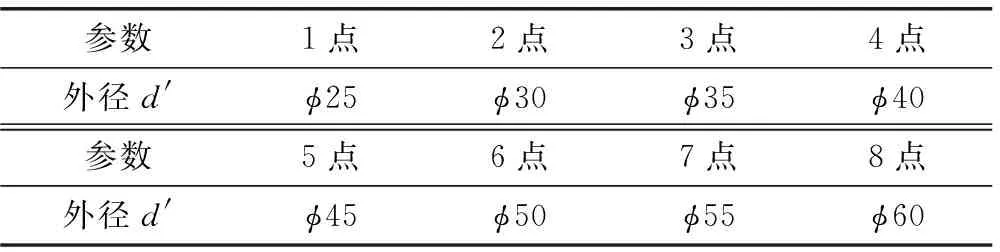
表7 空心穩定桿外徑d′取點表 mm

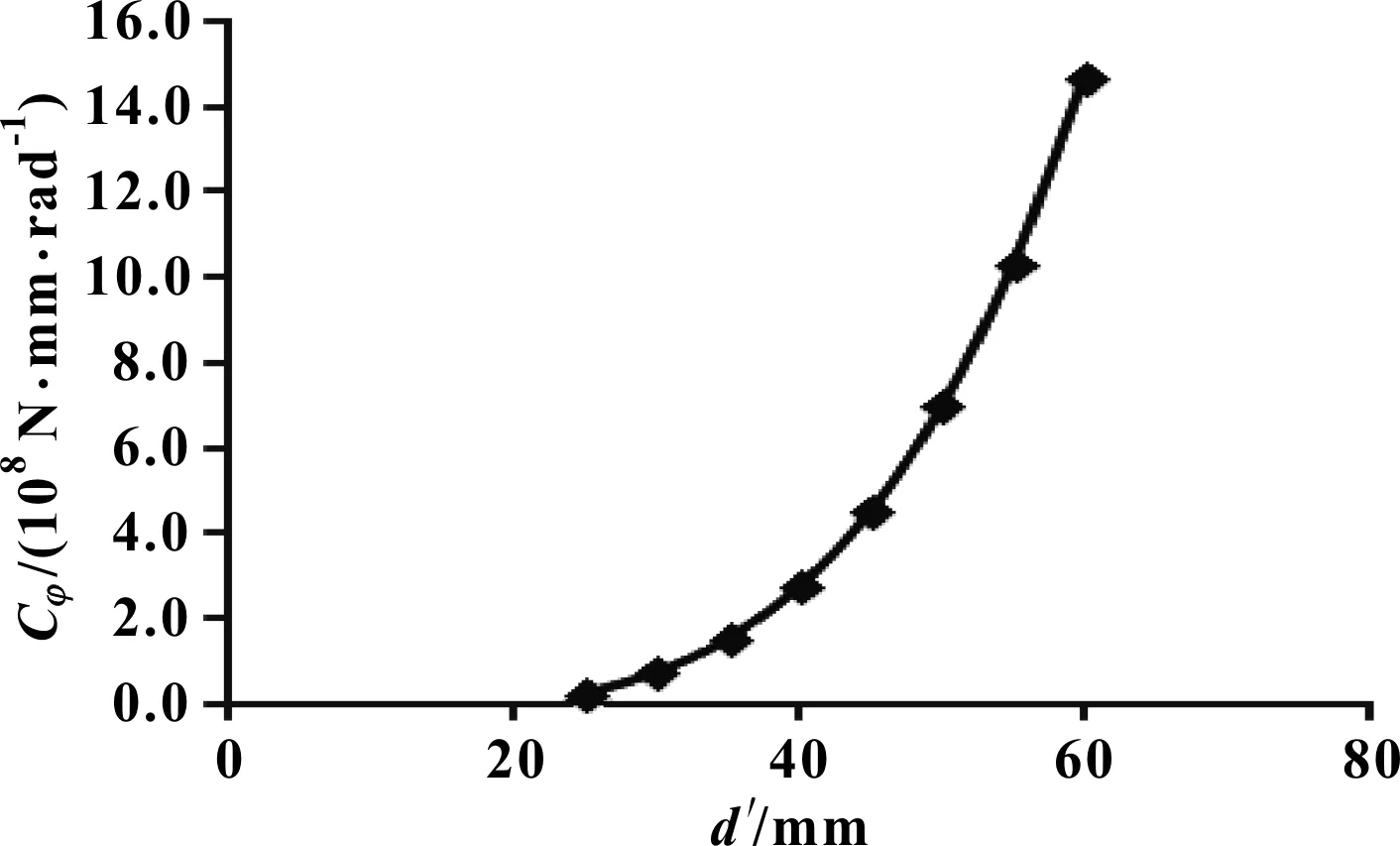
圖7 空心穩定桿外徑d′對穩定桿側傾剛度Cφ的影響曲線

分析圖7可知：在其他尺寸參數均保持不變的情況下，空心穩定桿的側傾剛度與其外徑d′的變化趨勢與圖6類似，隨著空心穩定桿外徑d′的增大，空心穩定桿的側傾剛度呈冪函數增長。當外徑d′與內徑D的差值逐漸變大，空心穩定桿的側傾剛度漲幅逐漸加劇。

3.2 空心穩定桿內徑D的影響曲線

在其他尺寸參數不變的情況下，取外徑d′=φ40 mm，保持不變。空心穩定桿內徑D的取點情況如表8所示。繪制空心穩定桿內徑D對橫向穩定桿側傾剛度的影響曲線，如圖8所示。

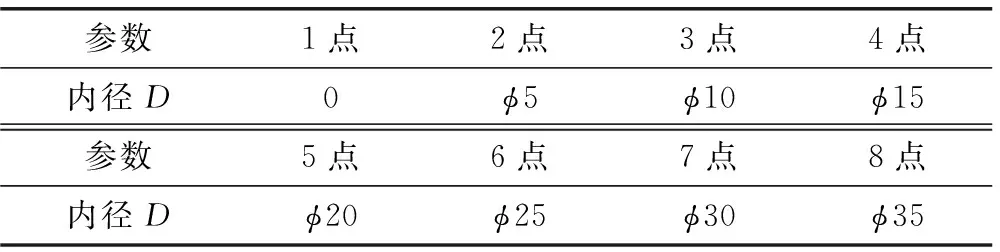
表8 空心穩定桿內徑D取點表 mm

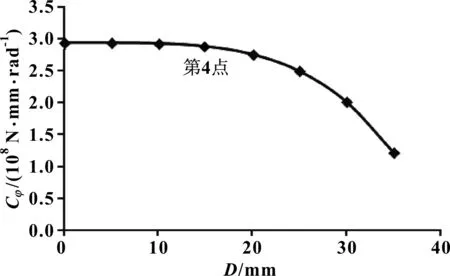
圖8 空心穩定桿內徑D對穩定桿側傾剛度Cφ的影響曲線

分析圖8可知：空心穩定桿的內徑D從第1點變化至第4點，其剛度降幅非常平緩，第4點為影響曲線的一個拐點；從第4點開始，隨著空心穩定桿內徑D增大，穩定桿側傾剛度降幅逐漸增大。

在其他參數不變的情況下，由圖8可知：空心穩定桿的內徑D不是越小越好。當保證空心穩定桿外徑d′=φ40 mm不變，內徑D取小于φ15 mm的任意值時，對穩定桿側傾剛度的影響甚微。因此，綜合考慮橫向穩定桿輕量化指標，在設計時，可以適當選擇空心穩定桿結構。根據圖8所示的影響曲線，選擇內徑D≤φ15 mm的空心穩定桿時，能夠得到與實心穩定桿相當的側傾剛度，同時，實現輕量化目標約達14%。

3.3 質量相同情況下實心桿與空心桿的比較分析

在穩定桿其他尺寸參數不變的情況下，穩定桿的截面積相等便可實現質量相等。在保證實心穩定桿與空心穩定桿截面積相等的情況下，實心穩定桿直徑d與空心穩定桿的內徑D和外徑d′的取點情況如表9所示。繪制兩種橫向穩定桿側傾剛度隨截面積的變化曲線，如圖9所示。

分析圖9可知：相同質量(截面積)的情況下，空心穩定桿的側傾剛度比實心穩定桿的側傾剛度普遍偏大。隨著截面積變大，空心穩定桿與實心穩定桿的側傾剛度的差值逐漸變大。因此，在保證相同的穩定桿總成側傾剛度的情況下，空心穩定桿的質量更輕，能夠更好地實現輕量化。

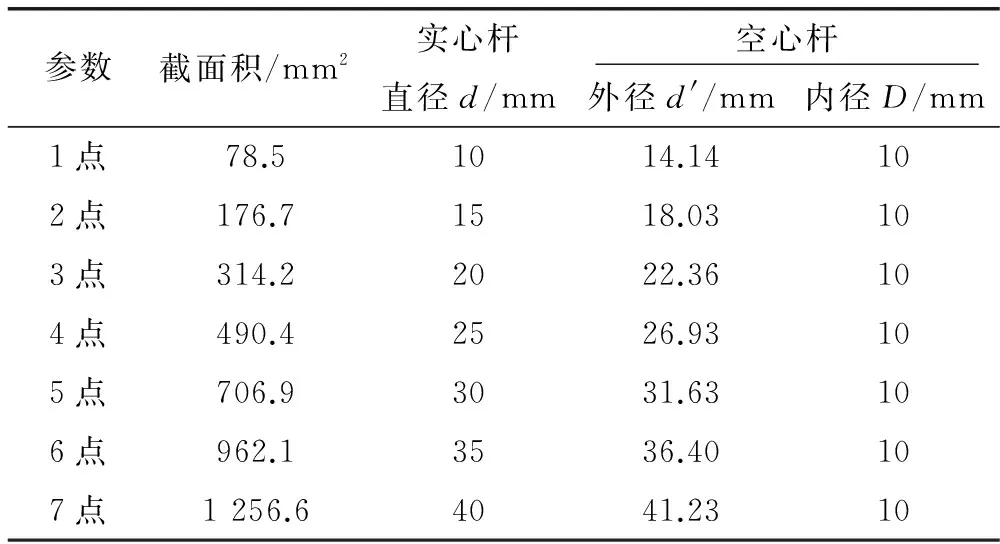
表9 相同質量(截面積)情況下，穩定桿直徑取點表

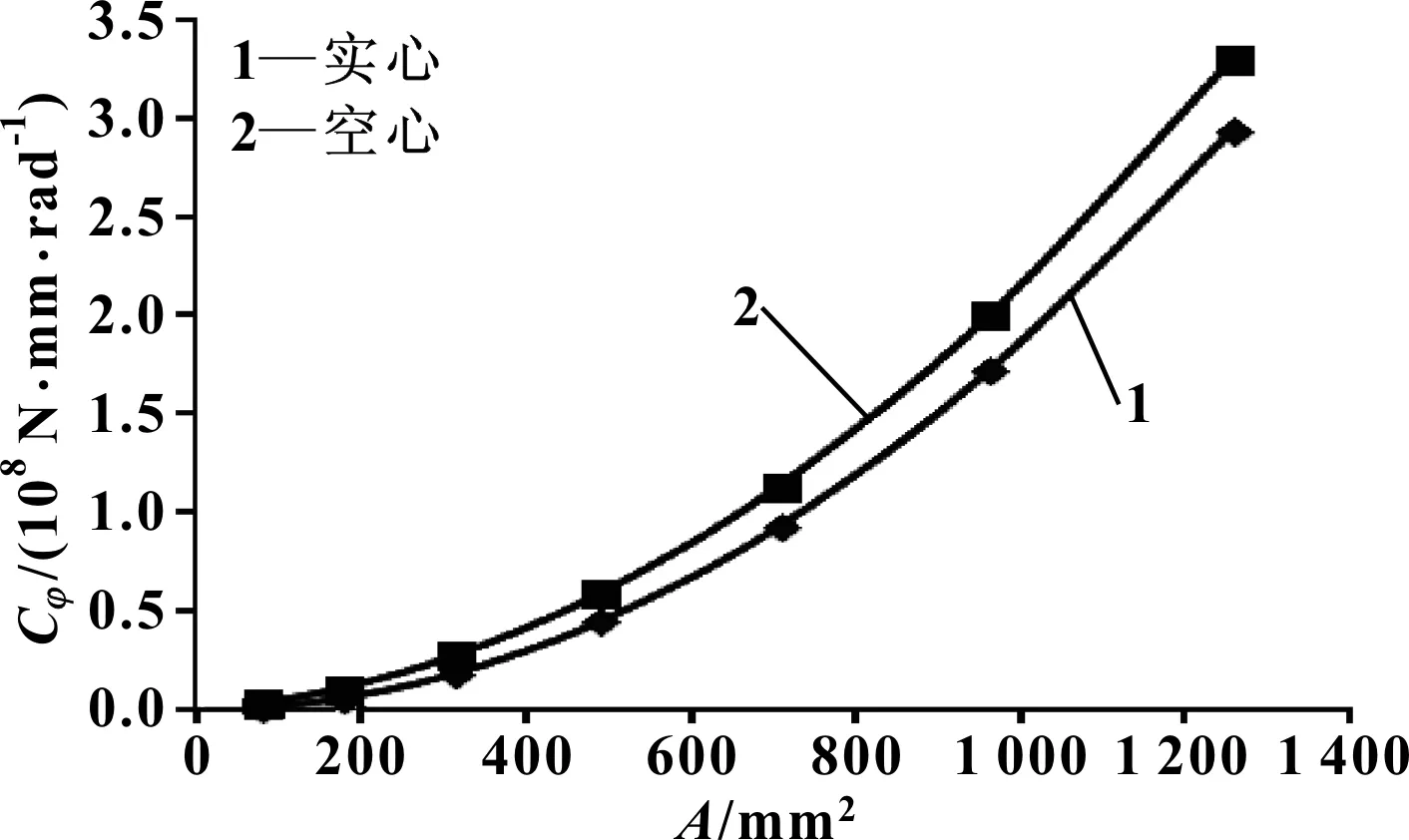
圖9 相同質量(截面積)情況下，實心桿與

4 形狀尺寸參數

4.1 梯形橫向穩定桿側傾剛度理論計算公式

近年來，商用車用橫向穩定桿逐漸從單一的直角形向梯形或者復雜形狀發展。梯形穩定桿由于性能良好、方便布置和制造，逐漸得到應用。

梯形穩定桿側傾剛度理論計算簡圖如圖10所示。

圖10 梯形橫向穩定桿示意圖

公式(1)是橫向穩定桿側傾剛度理論計算的通用公式，對于梯形橫向穩定桿依然適用，但是公式中的P和U有所不同。依據梯形橫向穩定桿自身的結構特點，根據能量原理，推導出公式(1)中，適用于梯形橫向穩定桿側傾剛度的P和U的公式，如下所示：

(4)

(5)

(6)

4.2 梯形穩定桿夾角θ的影響曲線

在其他尺寸參數不變的情況下(如表1)，夾角θ取點情況如表10所示。繪制夾角θ對梯形橫向穩定桿側傾剛度的影響曲線，如圖11所示。

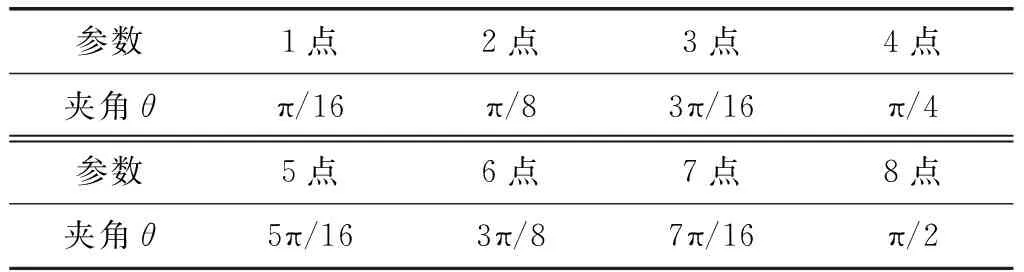
表10 夾角θ取點表 rad

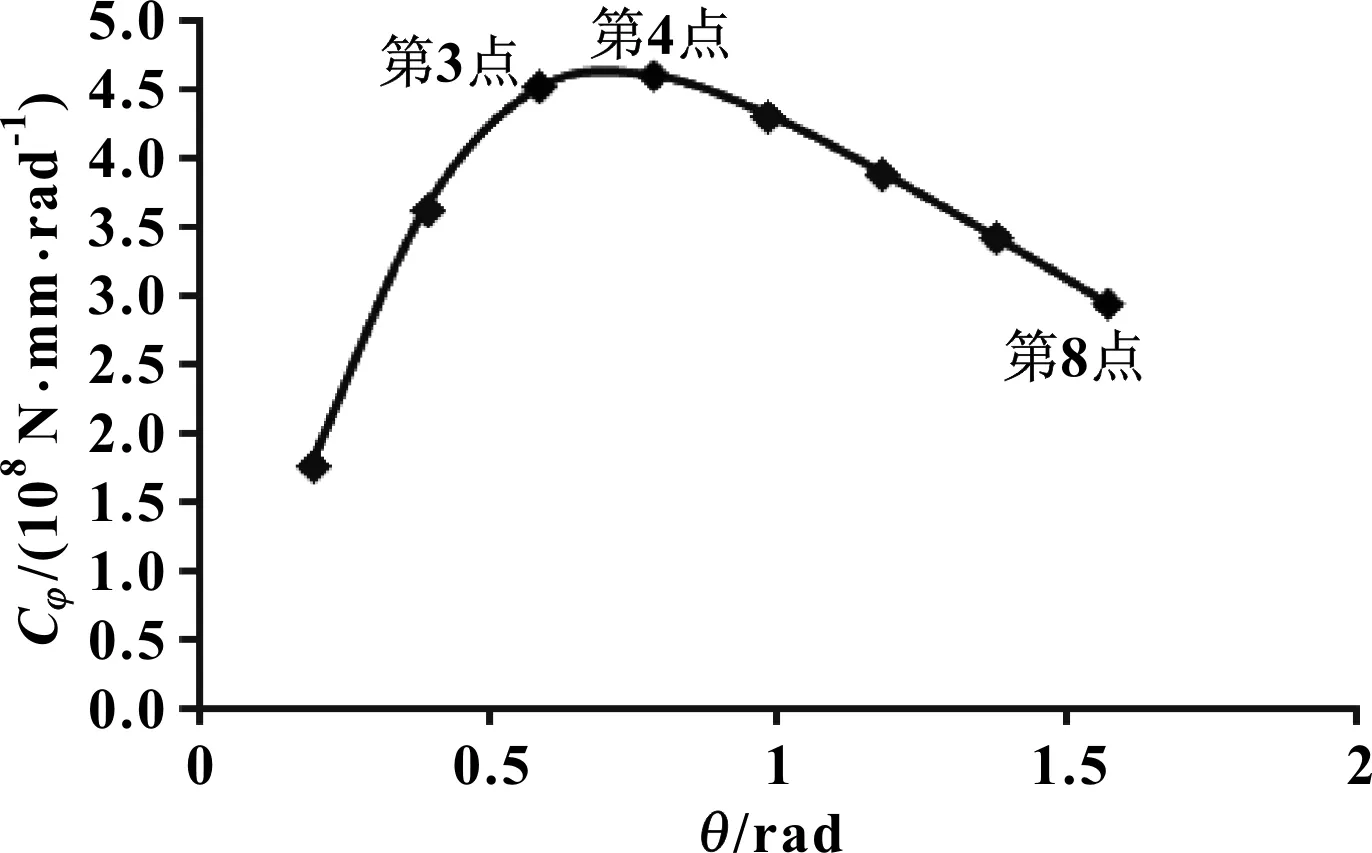
圖11 夾角θ對梯形橫向穩定桿側傾剛度Cφ的影響曲線

分析圖11可知：第4點(θ=π/4)是一個峰值點；夾角θ在第3點(θ=3π/16)與第4點(θ=π/4)間取值時，梯形穩定桿側傾剛度變化較平緩，是梯形橫向穩定桿夾角θ取值的合適區間；從第4點(θ=π/4)至第8點(θ=π/2)，隨著夾角θ增大，梯形橫向穩定桿的側傾剛度線性減小，直至第8點(θ=π/2)，此時穩定桿為直角形狀。由此可見：從第2點開始，即當π/8<θ<π/2時，梯形橫向穩定桿側傾剛度均比直角形橫向穩定桿(θ=π/2)側傾剛度大。因此，在設計橫向穩定桿時，綜合考慮其他因素，可適當選擇梯形橫向穩定桿，以便獲取更優的側傾剛度。選擇梯形穩定桿時，以夾角θ趨于π/4為宜。

5 驗證

目前國內、外市場上，商用車用橫向穩定桿的形狀大體分為直角形、類直角形、梯形或類梯形。截面積形式以實心為主，偶爾出現空心穩定桿。文中列舉國內、外不同廠家的橫向穩定桿的基本尺寸參數、截面尺寸參數和形狀尺寸參數，進行對比分析，便可對文中所繪制的尺寸參數影響曲線進行實際驗證。

對比分析表11可知：國內廠家B的尺寸參數L1取值明顯比其他3家偏大。根據圖2可知，單從穩定桿側傾剛度分析，廠家B選擇的尺寸參數L1不甚合理，其他3家選擇的L1在合理區域。

國內、外4個廠家對于尺寸參數L2的選擇一致性較好，與整車布置空間有關。

國內、外廠家對于尺寸參數L3的選擇存在較大分歧。根據圖4可知：L3越大，穩定桿側傾剛度會越小，影響曲線的拐點為L3=200 mm。由此可知，國外廠家選擇的尺寸參數L3較合理。一般情況下，盡可能不要選擇過大的L3，以免對穩定桿側傾剛度造成不良影響。

由表11可知：目前市場上，以直角形實心橫向穩定桿為主流形式。由于市場對輕量化的關注度不斷提升，空心穩定桿已逐漸出現，但并未被廣泛采用。

綜上所述：國外兩個廠家橫向穩定桿的尺寸參數基本遵循尺寸參數影響曲線的變化規律進行選擇，尺寸參數基本位于影響曲線的合理區域，參數一致性較好。國內兩個廠家橫向穩定桿部分尺寸參數離散性較大，根據尺寸參數影響曲線，還有進一步優化的空間。通過4個國內、外橫向穩定桿實際尺寸參數的對比分析，驗證了文中繪制的穩定桿尺寸參數影響曲線的正確性。同時，尺寸參數影響曲線對于穩定桿設計和優化都有較直觀和精確的指導意義。

6 結論

通過對橫向穩定桿的基本尺寸參數、截面尺寸參數和形狀尺寸參數的分析，從理論計算入手，得出各種尺寸參數對橫向穩定桿側傾剛度的影響曲線。文中得到以下幾點結論：

(1)基本尺寸參數(L1、L2、L3、R和d)對穩定桿側傾剛度的影響趨勢和影響程度各不相同。文中繪制的基本尺寸參數對穩定桿側傾剛度的影響曲線，能夠直觀、精確地判斷各基本尺寸參數對穩定桿側傾剛度的影響情況。在穩定桿設計初期，可方便、快捷、精準地確定各基本尺寸參數；

(2)空心穩定桿與實心穩定桿相比較，既能夠得到較優的側傾剛度，還能夠實現輕量化的目標，是穩定桿設計中的一個雙贏的方案；

(3)梯形穩定桿相較于傳統直角形穩定桿有更優的側傾剛度。當梯形穩定桿的夾角θ趨近π/4時，可獲得最優的側傾剛度；

(4)空心穩定桿及梯形穩定桿是橫向穩定桿發展的趨勢，設計時可根據文中繪制的不同參數的影響曲線，確定合適的尺寸參數；

(5)結合國內、外4個廠家橫向穩定桿尺寸參數，驗證了文中推導的尺寸參數影響曲線的正確性及其指導意義。

【1】曾林.車用穩定桿及其發展前景[J].彈簧工程，1993(2):2-8.

【2】黃康，仰榮德.基于ANSYS的汽車橫向穩定桿疲勞分析[J].機械設計,2008,25(12):66-68. HUANG K,YANG R D.Fatigue Analysis on the Automobile Transverse Stability Rod Based on ANSYS[J].Journal of Machine Design,2008,25(12):66-68.

【3】劉惟信.汽車設計[M].北京：清華大學出版社,2001:510-512.

【4】日本自動車技術會.汽車工程手冊5 底盤設計篇[M].中國汽車工程學會組,譯.北京：北京理工大學出版社,2010:31-33.

Analysis and Verification of the Dimension Parameter Impact on the Roll Stiffness of the Stabilizer Bar

WANG Xiaolian, ZHANG Xuebo

(Research & Development Center,China FAW Co., Ltd.,Changchun Jilin 130011,China)

In the stabilizer bar design process, the choice of the dimension parameter impacts the roll stiffness of the stabilizer bar directly. The roll stiffness of the stabilizer bar is affected by many dimension parameters. The calculating formula is complex, it is difficult to choose the dimension parameter intuitively in initial stage design. Based on theoretical calculation, the influence curves which single parameter impacted on the roll stiffness of the stabilizer bar were drawn. The curves could be used to judge the influence degree which different parameters impacted on the roll stiffness of the stabilizer bar. Combining the actual dimension parameters of domestic and foreign products, through comparative analysis, the correctness of the influence curves was verified. The problem that is difficult to choose and optimize dimension parameters accurately in initial design stage is solved.

Stabilizer bar; Roll stiffness; Dimension parameter; Influence curve

2017-01-11

王曉蓮(1984—)，女，碩士，工程師，研究方向為懸架系統設計與開發、整車可靠性開發及對標等。E-mail：wangxiaolian@rdc.faw.com.cn。

10.19466/j.cnki.1674-1986.2017.05.006

U463.33

A

1674-1986(2017)05-028-06