Ma-Minda型雙向單葉螺旋函數類的Fekete-Szeg?不等式

湯獲, 李文娟, 張海燕, 周海燕

(1.赤峰學院數學與統計學院,內蒙古赤峰 024000;2.赤峰學院應用數學研究所,內蒙古赤峰 024000)

Ma-Minda型雙向單葉螺旋函數類的Fekete-Szeg?不等式

湯獲1,2, 李文娟1,2, 張海燕1,2, 周海燕1,2

(1.赤峰學院數學與統計學院,內蒙古赤峰 024000;2.赤峰學院應用數學研究所,內蒙古赤峰 024000)

引入單位圓盤 D={z∈C:|z|<1}內 Ma-Minda型雙向單葉螺旋函數類(λ,β,φ),利用從屬關系討論了該類中函數的Fekete-Szeg¨o不等式,所得結果推廣了一些作者的相關工作.

解析函數;Ma-Minda型雙向單葉螺旋函數;從屬關系;Fekete-Szeg¨o不等式

1 引言

設 R是實數集,C是復數集,N={1,2,3,···}=N0{0}是正整數集,A表示在單位圓盤D={z∈C:|z|<1}內具有如下形式:

的解析函數族.用S表示在D內單葉且滿足A的所有子類.對于任意函數f∈S,它是可逆的且其逆函數f?1滿足:

和

這里

如果函數f和f?1在D內單葉,則稱函數f∈A在D內雙向單葉[1].用σ表示D內雙向單葉函數類.

設函數f(z)和g(z)在D內解析,若存在一個Schwarz函數w(z),使得

滿足

則稱函數g(z)從屬于f(z),記為g(z)?f(z)(見文獻[2])．

利用從屬定義,在文獻[3]中引入如下的Ma-Minda型星象函數和Ma-Minda型凸象函數:

其中 φ(z)是在D 內實部為正的解析函數,且滿足 φ(0)=1,φ′(0)>0,φ(z)將D 映射到關于1星象和實軸對稱的一個區域.

若 f和 f?1是 Ma-Minda型星象函數,則稱 f是 Ma-Minda型雙向星象函數,記為(見文獻[3]);若f和f?1是Ma-Minda型凸象函數,則稱f是Ma-Minda型雙向凸象函數,記為 Kσ(φ)(見文獻[3]).

近年來,許多學者引入并研究了雙向單葉函數的各種子類[4-6],并得到了該類中函數系數|a2|和|a3|的估計.最近,文獻[7-10]借助從屬關系討論了某些廣義雙向單葉函數類中函數系數|a2|和|a3|的估計.受上述工作的啟發,本文引進并研究一類Ma-Minda型雙向單葉螺旋函數類,利用從屬關系討論該類中函數的Fekete-Szeg¨o不等式,所得結果推廣一些已知結果.

2 主要結果

假設 φ(z)是在 D 內的正實部單葉解析函數,且 φ(0)=1,φ′(0)>0,φ(z)映射單位圓盤D到D內的星形區域是關于實軸對稱的星象域,其泰勒級數展開式具有如下形式:

其中 Bj∈ R(j=1,2,···),B1>0.

下面引入Ma-Minda型雙向單葉螺旋函數類.

定義 2.1設函數f(z)∈σ由(1.1)式給出,如果函數f(z)滿足下列條件:

和

注 2.1在定義2.1中,若適當選取參數λ,β和φ,可得下列函數子類:

為了得出本文主要結果,需要以下引理.

引理2.1[2]設函數

為 D 內正實部解析函數,則 |pj|≤2(j=1,2,···).

定理2.1設δ∈R,函數f由(1)式給出,若則有

定義兩個函數p和q如下:

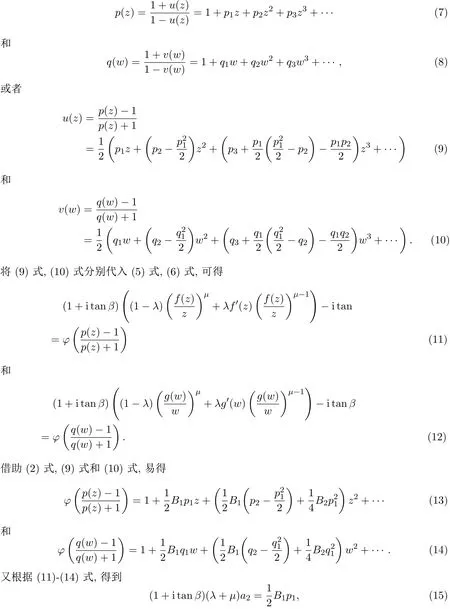
定理2.1得證.證畢.

在定理2.1中,若取β=0,則有下列推論2.1.

推論2.1設δ∈R,函數f由(1)式給出,若則有

在定理2.1中,若取μ=1,則有下列推論2.2.

推論 2.2設 δ∈R,函數 f由 (1)式給出,若 f∈Hσ(λ,β,φ),則有

在定理2.1中,若取λ=1,則有下列推論2.3.

推論2.3設 δ∈R,函數f由(1)式給出,若f∈(β,φ),則有

在定理2.1中,若取μ=λ=1,則有下列推論2.4.

推論 2.4設 δ∈R,函數 f由 (1)式給出,若 f∈Hσ(β,φ),則有

在定理2.1中,若取δ=1,則有下列推論2.5.

推論2.5設函數f由(1)式給出,若f∈(λ,β,φ),則有

[1]Lewin M.On a coefficient problem for bi-univalent functions[J].Proc.Am.Math.Soc.,1967,18:63-68.

[2]Duren P L.Univalent Functions[M].Berlin:Springer,1983.

[3]Ma W C,Minda D.A uni fi ed Treatment of Some Special Classes of Univalent Functions[M].England:Cambridge,1994.

[4]Srivastava H M,Mishra A K,Gochhayat P.Certain subclasses of analytic and bi-univalent functions[J].Appl.Math.Lett.,2010,23:1188-1192.

[5]Frasin B A,Aouf M K.New subclasses of bi-univalent functions[J].Appl.Math.Lett.,2011,24:1569-1573.

[6]Caglar M,Orhan H,Yagmur N.Coefficient bounds for new subclasses of bi-univalent functions[J].Filomat.,2013,7:1165-1171.

[7]Ali R M,Lee S K,Ravichandran V,et al.Coefficient estimates for bi-univalent Ma-Minda starlike and convex functions[J].Appl.Math.Lett.,2012,25:344-351.

[8]Xu Q H,Xiao H G,Srivastava H M.A certain general subclass of analytic and bi-univalent functions and associated coefficient estimate problems[J].Appl.Math.Comput.,2012,218:11461-11465.

[9]Xu Q H,Gui Y C,Srivastava H M.Coefficient estimates for a certain subclass of analytic and bi-univalent functions[J].Appl.Math.Lett.,2012,25:990-994.

[10]Tang Huo,Deng Guantie,Li Shuhai.Coefficient estimates for new subclass of Ma-Minda bi-univalent functions[J].J.Ineq.Appl.,2013,317:1-10.

Fekete-Szeg? inequalities for the class of Ma-Minda bi-univalent spirlike functions

Tang Huo1,2,Li Wenjuan1,2,Zhang Haiyan1,2,Zhou Haiyan1,2
(1.School of Mathematics and Statistics,Chifeng University,Chifeng 024000,China;2.Institute of Applied Mathematics,Chifeng University,Chifeng 024000,China)

In this paper,we introduce the class Hμσ(λ,β,φ)of Ma-Minda bi-univalent spirlike functions in the open unit disk D={z ∈ C:|z|<1}.By using the subordination relationship,we investigate Fekete-Szeg¨o inequalities for functions belonging to the above class.The results obtained generalize some known works.

Ma-Minda bi-univalent spirlike function,subordination relationship,Fekete-Szeg¨o inequality

O174.51

A

1008-5513(2017)03-0241-07

10.3969/j.issn.1008-5513.2017.03.003

2017-03-13.

國家自然科學基金(11561001);內蒙古自然科學基金(2014MS0101);內蒙古高校科研基金(NJZY16251).

湯獲(1979-),博士,副教授,研究方向:復分析及其應用.

2010 MSC:16D13