基于可變形卷積神經(jīng)網(wǎng)絡(luò)的圖像分類研究

歐陽針+陳瑋

摘要：卷積神經(jīng)網(wǎng)絡(luò)（Convolutional Neural Networks，CNNs）具有強(qiáng)大的特征自學(xué)習(xí)與抽象表達(dá)能力，在圖像分類領(lǐng)域有著廣泛應(yīng)用。但是，各模塊較為固定的幾何結(jié)構(gòu)完全限制了卷積神經(jīng)網(wǎng)絡(luò)對(duì)空間變換的建模，難以避免地受到數(shù)據(jù)空間多樣性的影響。在卷積網(wǎng)絡(luò)中引入自學(xué)習(xí)的空間變換結(jié)構(gòu)，或是引入可變形的卷積，使卷積核形狀可以發(fā)生變化，以適應(yīng)不同的輸入特征圖，豐富了卷積網(wǎng)絡(luò)的空間表達(dá)能力。對(duì)現(xiàn)有卷積神經(jīng)網(wǎng)絡(luò)進(jìn)行了改進(jìn)，結(jié)果表明其在公共圖像庫和自建圖像庫上都表現(xiàn)出了更好的分類效果。

關(guān)鍵詞：卷積神經(jīng)網(wǎng)絡(luò)；圖像分類；空間變換；可變形卷積

DOIDOI：10.11907/rjdk.171863

中圖分類號(hào)：TP317.4

文獻(xiàn)標(biāo)識(shí)碼：A 文章編號(hào)：1672-7800（2017）006-0198-04

0 引言

圖像分類一直是計(jì)算機(jī)視覺領(lǐng)域的一個(gè)基礎(chǔ)而重要的核心問題，具有大量的實(shí)際應(yīng)用場(chǎng)景和案例。很多典型的計(jì)算機(jī)視覺問題（如物體檢測(cè)、圖像分割）都可以演化為圖像分類問題。圖像分類問題有很多難點(diǎn)需要解決，觀測(cè)角度、光照條件的變化、物體自身形變、部分遮擋、背景雜波影響、類內(nèi)差異等問題都會(huì)導(dǎo)致被觀測(cè)物體的計(jì)算機(jī)表示（二維或三維數(shù)值數(shù)組）發(fā)生劇烈變化。一個(gè)良好的圖像分類模型應(yīng)當(dāng)對(duì)上述情況（以及不同情況的組合）不敏感。使用深度學(xué)習(xí)尤其是深度卷積神經(jīng)網(wǎng)絡(luò)，用大量圖像數(shù)據(jù)進(jìn)行訓(xùn)練后可以處理十分復(fù)雜的分類問題。

卷積神經(jīng)網(wǎng)絡(luò)是為識(shí)別二維形狀而專門設(shè)計(jì)的一個(gè)多層感知器，這種網(wǎng)絡(luò)結(jié)構(gòu)對(duì)平移、縮放、傾斜等擾動(dòng)具有高度不變性，并且具有強(qiáng)大的特征學(xué)習(xí)與抽象表達(dá)能力，可以通過網(wǎng)絡(luò)訓(xùn)練獲得圖像特征，避免了復(fù)雜的特征提取與數(shù)據(jù)重建過程。通過網(wǎng)絡(luò)層的堆疊，集成了低、中、高層特征表示。AlexNet等網(wǎng)絡(luò)模型的出現(xiàn)，也推動(dòng)了卷積網(wǎng)絡(luò)在海量圖像分類領(lǐng)域的蓬勃發(fā)展。

1 卷積神經(jīng)網(wǎng)絡(luò)

卷積神經(jīng)網(wǎng)絡(luò)是人工神經(jīng)網(wǎng)絡(luò)的一種，其“局部感知”“權(quán)值共享”[1]等特性使之更類似于生物神經(jīng)網(wǎng)絡(luò)，網(wǎng)絡(luò)模型復(fù)雜度大大降低，網(wǎng)絡(luò)訓(xùn)練更容易，多層的網(wǎng)絡(luò)結(jié)構(gòu)有更好的抽象表達(dá)能力，可以直接將圖像作為網(wǎng)絡(luò)輸入，通過網(wǎng)絡(luò)訓(xùn)練自動(dòng)學(xué)習(xí)圖像特征，從而避免了復(fù)雜的特征提取過程。

Yann LeCun等[2]設(shè)計(jì)的LeNet-5是當(dāng)前廣泛使用的卷積網(wǎng)絡(luò)結(jié)構(gòu)原型，它包含了卷積層、下采樣層（池化層）、全連接層以及輸出層，構(gòu)成了現(xiàn)代卷積神經(jīng)網(wǎng)絡(luò)的基本組件，后續(xù)復(fù)雜的模型都離不開這些基本組件。LeNet-5對(duì)手寫數(shù)字識(shí)別率較高，但在大數(shù)據(jù)量、復(fù)雜的物體圖片分類方面不足，過擬合也導(dǎo)致其泛化能力較弱。網(wǎng)絡(luò)訓(xùn)練開銷大且受制于計(jì)算機(jī)性能。

2012年，在ILSVRC競(jìng)賽中AlexNet模型[3]贏得冠軍，將錯(cuò)誤率降低了10個(gè)百分點(diǎn)。擁有5層卷積結(jié)構(gòu)的AlexNet模型證明了卷積神經(jīng)網(wǎng)絡(luò)在復(fù)雜模型下的有效性，并將GPU訓(xùn)練引入研究領(lǐng)域，使得大數(shù)據(jù)訓(xùn)練時(shí)間縮短，具有里程碑意義。AlexNet還有如下創(chuàng)新點(diǎn)：①采用局部響應(yīng)歸一化算法（Local Response Normalization，LRN），增強(qiáng)了模型的泛化能力，有效降低了分類錯(cuò)誤率；②使用Dropout技術(shù)，降低了神經(jīng)元復(fù)雜的互適應(yīng)關(guān)系，有效避免了過擬合；③為了獲得更快的收斂速度，AlexNet使用非線性激活函數(shù)ReLU（Rectified Linear Units）來代替?zhèn)鹘y(tǒng)的Sigmoid激活函數(shù)。

Karen等[4]在AlexNet的基礎(chǔ)上使用更小尺寸的卷積核級(jí)聯(lián)替代大卷積核，提出了VGG網(wǎng)絡(luò)。雖然VGG網(wǎng)絡(luò)層數(shù)和參數(shù)都比AlexNet多，但得益于更深的網(wǎng)絡(luò)和較小的卷積核尺寸，使之具有隱式規(guī)則作用，只需很少的迭代次數(shù)就能達(dá)到收斂目的。

復(fù)雜的網(wǎng)絡(luò)結(jié)構(gòu)能表達(dá)更高維的抽象特征。然而，隨著網(wǎng)絡(luò)層數(shù)增加，參數(shù)量也急劇增加，導(dǎo)致過擬合及計(jì)算量大增，解決這兩個(gè)缺陷的根本辦法是將全連接甚至一般的卷積轉(zhuǎn)化為稀疏連接。為此，Google團(tuán)隊(duì)提出了Inception結(jié)構(gòu)[5]，以將稀疏矩陣聚類為較為密集的子矩陣來提高計(jì)算性能。以Inception結(jié)構(gòu)構(gòu)造的22層網(wǎng)絡(luò)GoogLeNet，用均值池化代替后端的全連接層，使得參數(shù)量只有7M，極大增強(qiáng)了泛化能力，并增加了兩個(gè)輔助的Softmax用于向前傳導(dǎo)梯度，避免梯度消失。GoogLeNet在2014年的ILSVRC競(jìng)賽中以Top-5錯(cuò)誤率僅6.66%的成績(jī)摘得桂冠。

網(wǎng)絡(luò)層數(shù)的增加并非永無止境。隨著網(wǎng)絡(luò)層數(shù)的增加，將導(dǎo)致訓(xùn)練誤差增大等所謂退化問題。為此，微軟提出了一種深度殘差學(xué)習(xí)框架[6]，利用多層網(wǎng)絡(luò)擬合一個(gè)殘差映射，成功構(gòu)造出152層的ResNet-152，并在2015年的ILSVRC分類問題競(jìng)賽中取得Top-5錯(cuò)誤率僅5.71%的成績(jī)。隨后，對(duì)現(xiàn)有的瓶頸式殘差結(jié)構(gòu)進(jìn)行改進(jìn)，提出了一種直通結(jié)構(gòu)[7]，并基于此搭建出驚人的1001層網(wǎng)絡(luò)，在CIFAR-10分類錯(cuò)誤率僅4.92%。至此，卷積神經(jīng)網(wǎng)絡(luò)在越來越“深”的道路上一往直前。

2 可變形的卷積神經(jīng)網(wǎng)絡(luò)

2.1 空間變換網(wǎng)絡(luò)

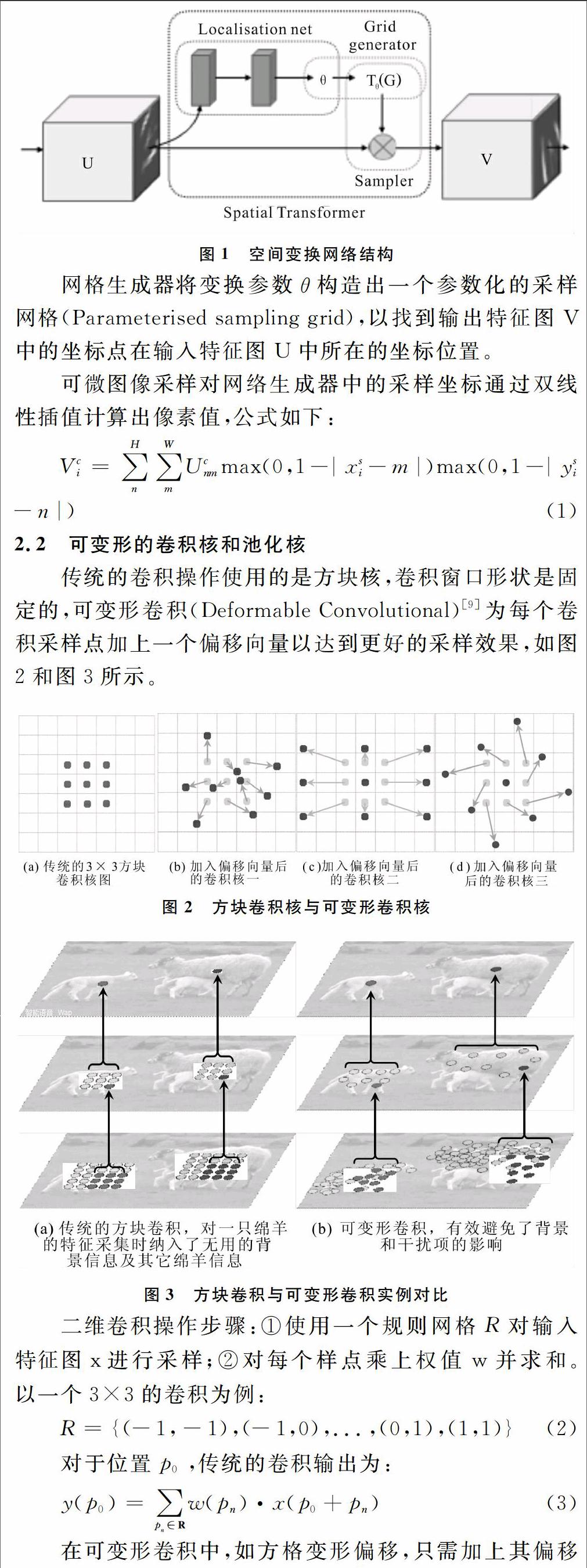
空間變換網(wǎng)絡(luò)（Spatial Transformer Network，STN）[8]主要由定位網(wǎng)絡(luò)（Localisation net）、網(wǎng)格生成器（Grid generator）和可微圖像采樣（Differentiable Image Sampling）3部分構(gòu)成，如圖1所示。

定位網(wǎng)絡(luò)將輸入的特征圖U放入一個(gè)子網(wǎng)絡(luò)（由卷積、全連接等構(gòu)成的若干層子網(wǎng)絡(luò)），生成空間變換參數(shù)θ。θ的形式可以多樣，如需要實(shí)現(xiàn)2D仿射變換，那么θ就是一個(gè)2×3的向量。

2.3 本文模型

本文以自建的3層卷積網(wǎng)絡(luò)C3K5（如圖6所示）和VGG-16作為基準(zhǔn)網(wǎng)絡(luò)，分別引入空間變換網(wǎng)絡(luò)、可變形卷積和可變形池化，構(gòu)造出8個(gè)卷積神經(jīng)網(wǎng)絡(luò)，用以驗(yàn)證可變形模塊對(duì)淺層網(wǎng)絡(luò)和深層網(wǎng)絡(luò)的影響，如表1所示。

圖6中C3K5網(wǎng)絡(luò)模型包含3個(gè)帶有ReLU層、LRN層和池化層的卷積模塊，卷積層采用步長(zhǎng)為1的5×5卷積核，輸出保持原大小，池化層采用步長(zhǎng)為2核為2×2的最大值池化，即每經(jīng)過一個(gè)卷積模塊，特征圖縮小為原來的一半。

3 實(shí)驗(yàn)與分析

3.1 實(shí)驗(yàn)設(shè)置

本文實(shí)驗(yàn)環(huán)境：CPU為Intel i5-7400，8G內(nèi)存，顯卡為GTX1060，采用Cuda8+CuDNN6.0加速。

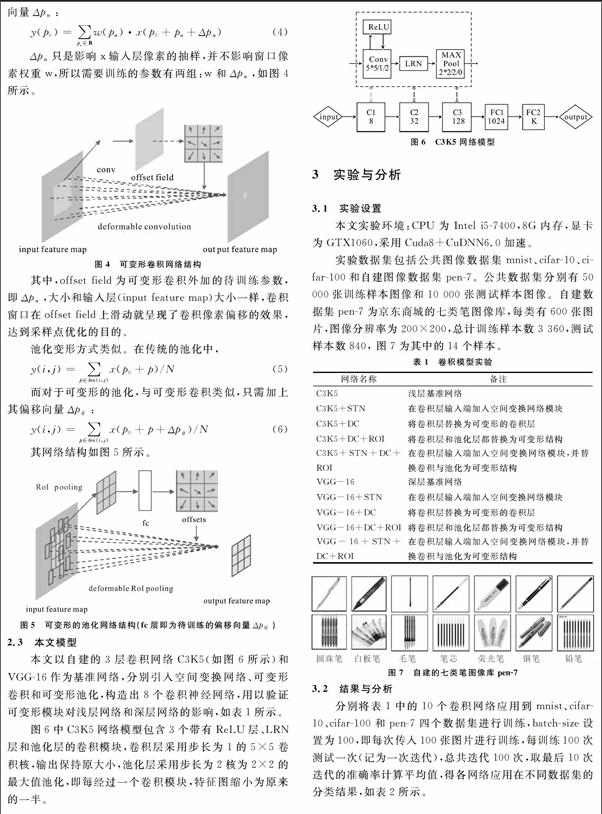
實(shí)驗(yàn)數(shù)據(jù)集包括公共圖像數(shù)據(jù)集mnist、cifar-10、cifar-100和自建圖像數(shù)據(jù)集pen-7。公共數(shù)據(jù)集分別有50 000張訓(xùn)練樣本圖像和10 000張測(cè)試樣本圖像。自建數(shù)據(jù)集pen-7為京東商城的七類筆圖像庫，每類有600張圖片，圖像分辨率為200×200，總計(jì)訓(xùn)練樣本數(shù)3 360，測(cè)試樣本數(shù)840， 圖7為其中的14個(gè)樣本。

3.2 結(jié)果與分析

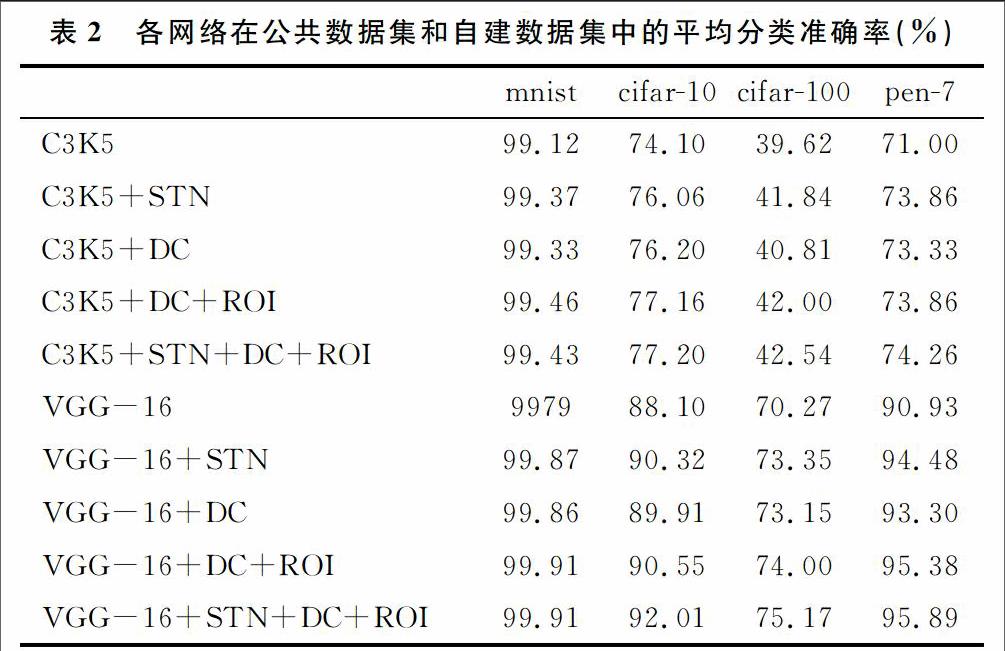
分別將表1中的10個(gè)卷積網(wǎng)絡(luò)應(yīng)用到mnist、cifar-10、cifar-100和pen-7四個(gè)數(shù)據(jù)集進(jìn)行訓(xùn)練，batch-size設(shè)置為100，即每次傳入100張圖片進(jìn)行訓(xùn)練，每訓(xùn)練100次測(cè)試一次（記為一次迭代），總共迭代100次，取最后10次迭代的準(zhǔn)確率計(jì)算平均值，得各網(wǎng)絡(luò)應(yīng)用在不同數(shù)據(jù)集的分類結(jié)果，如表2所示。

實(shí)驗(yàn)結(jié)果表明，在卷積網(wǎng)絡(luò)中引入空間變換網(wǎng)絡(luò)、用可變形的卷積層和可變形的池化層替換傳統(tǒng)的卷積層和池化層，不管是在淺層網(wǎng)絡(luò)還是在深層網(wǎng)絡(luò)，都能獲得更高的分類準(zhǔn)確率，這驗(yàn)證了空間變換網(wǎng)絡(luò)和可變形卷積（池化）結(jié)構(gòu)，豐富了卷積神經(jīng)網(wǎng)絡(luò)的空間特征表達(dá)能力，提升了卷積網(wǎng)絡(luò)對(duì)樣本的空間多樣性變化的魯棒性。包含3種模塊的網(wǎng)絡(luò)獲得了最高的分類精度，使空間變換網(wǎng)絡(luò)、可變形卷積層和可變形池化層在更多應(yīng)用場(chǎng)景中并駕齊驅(qū)成為可能。

4 結(jié)語

通過在現(xiàn)有卷積神經(jīng)網(wǎng)絡(luò)中引入空間變換網(wǎng)絡(luò)、可變形的卷積層和可變形的池化層，使得卷積網(wǎng)絡(luò)在mnist、cifar-10、cifar-100及自建的pen-7數(shù)據(jù)集中獲得了更高的分類精度，包含3種模塊的網(wǎng)絡(luò)獲得了最高分類精度，證明了空間變換網(wǎng)絡(luò)、可變形的卷積層和可變形池化層都能豐富網(wǎng)絡(luò)的空間特征表達(dá)能力，協(xié)同應(yīng)用于圖像分類工作，這為后續(xù)研究打下了堅(jiān)實(shí)的基礎(chǔ)。

參考文獻(xiàn)：

[1]BOUVRIE J. Notes on convolutional neural networks[J].Neural Nets，2006（1）：159-164.

[2]Y LECUN，L BOTTOU，Y BENGIO，et al.Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE， 1998， 86（11）： 2278-2324.

[3]KRIZHEVSKY A， SUTSKEVER I， HINTON G E. ImageNet classification with deep convolutional neural networks[C]. International Conference on Neural Information Processing Systems. Curran Associates Inc，2012：1097-1105.

[4]SIMONYAN K， ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[J]. Computer Science， 2014（6）：1211-1220.

[5]SZEGEDY C， LIU W， JIA Y， et al. Going deeper with convolutions[J]. CVPR， 2015（3）：1-9.

[6]HE K， ZHANG X， REN S， et al. Deep residual learning for image recognition[C]. Computer Vision and Pattern Recognition. IEEE， 2015：770-778.

[7]HE K， ZHANG X， REN S， et al. Identity mappings in deep residual networks[J]. arXiv，2016（1603）：5-27.

[8]JADERBERG M， SIMONYAN K， ZISSERMAN A， et al. Spatial transformer networks[J].Computer Science， 2015（5）：1041-1050.

[9]DAI J， QI H， XIONG Y， et al. Deformable convolutional networks[J]. arXiv： 2017（1703）：62-111.

（責(zé)任編輯：杜能鋼）

英文摘要Abstract：Convolutional neural networks （CNNs） have powerful abilities of self-learning and abstract expression and they have gained extensive research and wide application in the field of image classification. However， since each module has a fixed geometric structure， it fundamentally limits the modeling of spatial transformation by convolutional neural networks， and is inevitably affected by the spatially diversity of data. The involve of a self-learning spatial transform structure and the deformable convolutional which can change its shape to adapt different input feature are both enrich the spatial expression ability of convolutional networks. In combination with the two characteristics， the existing convolutional neural networks are improved， and a better classification result is obtained in both the public image library and my own image library.

英文關(guān)鍵詞Key Words： Convolutional Neural Network； Image Classification； Spatial Transform； Deformable Convolutional