優化的新陳代謝GM(1，1)模型在基坑變形監測中的應用

江寶鋒 錢傳俊 楊 劍

(長江水利委員會水文局長江口水文水資源勘測局,上海 200136)

優化的新陳代謝GM(1，1)模型在基坑變形監測中的應用

江寶鋒 錢傳俊 楊 劍

(長江水利委員會水文局長江口水文水資源勘測局,上海 200136)

針對傳統的GM(1，1)模型確定積分常數C缺乏一定理論依據的問題，依據建模方差最小原則優化傳統GM(1,1)模型的初始值，融合新陳代謝和新信息優先建模的思想，建立基于優化初始值的新陳代謝GM(1，1)模型，并將其應用到基坑變形監測中。結果表明，優化初始值的新陳代謝GM(1,1)模型預報精度優于傳統的GM(1,1)模型、新陳代謝GM(1，1)模型和優化初始值的GM(1,1)模型。

GM(1，1)模型；基坑變形；變形監測

隨著城市化進程的加快，大型基坑工程越來越多，而基坑的施工會給周邊的建筑物帶來安全隱患，因此對基坑進行實時變形監測，分析處理實測數據并進行變形預報具有重要意義。如何根據已測沉降數據建立科學、合理的預測模型，是當前測繪工作者研究的熱點之一。

GM(1,1)是目前應用最廣泛的模型，研究的是貧信息建模，對處理趨勢性變形和小子樣監測離散數據具有獨特優勢[1-2]，但是預測精度隨時間的推移會越來越低，實用性有待提高。鑒于傳統的GM(1,1)模型通常以第一點作為初始值來確定白化權函數中的常數C，但缺乏一定的理論依據，本文基于最小二乘約束的初始條件選取GM(1,1)模型的初始值，在預測過程中降低原點誤差，同時融合新陳代謝和新信息優先建模的思想，建立基于此優化值的新陳代謝GM(1,1)模型，從而有效提高預測精度。

1 數學模型建立

設觀測原始序列：

(1)

對x(0)作一次累加生成得到一個生成序列

(2)

對此建立一階微分方程

(3)

式中，a和u是灰參數，通過最小二乘估計可得

(4)

式中，

(5)

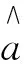
(6)

式中，C為常數，需要由初始值來確定[1-2]，通常確定白化權函數中常數C的方法理論依據不足，因此根據建模方差的概念，定義用于建模的數據資料與建模后所生成數據資料的真誤差平方和數學期望[3-4]，記為δ2。根據定義有

(7)

在δ2為最小的限定條件下，對C求偏導，并另

所以常數C的值

(8)

把式(8)代入式(7)并還原預測，即可得到優化的GM(1，1)模型。

(9)

(k=1,2，…，N)

模型的精度用后驗差方法檢驗[2]。設由已優化初始值的GM(1，1)模型得到

(10)

計算殘差

(11)

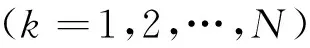
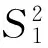
(12)

(13)

式中，

(14)

然后計算后驗差比值

(15)

和小誤差概率

(16)

表1列出了根據C、P取值的模型精度等級。 模型精度等級為max{P所在的級別，C所在的級別}。

表1 模型精度等級

隨著時間的推移，系統狀態隨著干擾系統的因素變化而變化[5-6]。即使仍采用已優化初始值的GM(1，1)模型，不僅模型的預測精度不斷降低，且其預測可靠度也在下降。要避免模型精度的損失，就要盡量利用最新已知或灰色信息來淡化灰平面的灰度，因此及時引入了新的已知或灰色信息，淘汰作用弱的信息，正確反應系統狀態[7]。

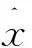
2 案例分析

本文以山東省聊城市公交集團調度中心施工基坑1號和10號監測點的監測數據為例進行模型分析。該基坑周圍有居民樓和辦公用樓，在基坑施工期間布設18個監測點，點編號1～18 。每期觀測時間間隔為1 d。表2為1號和10號監測點的部分沉降觀測數據。

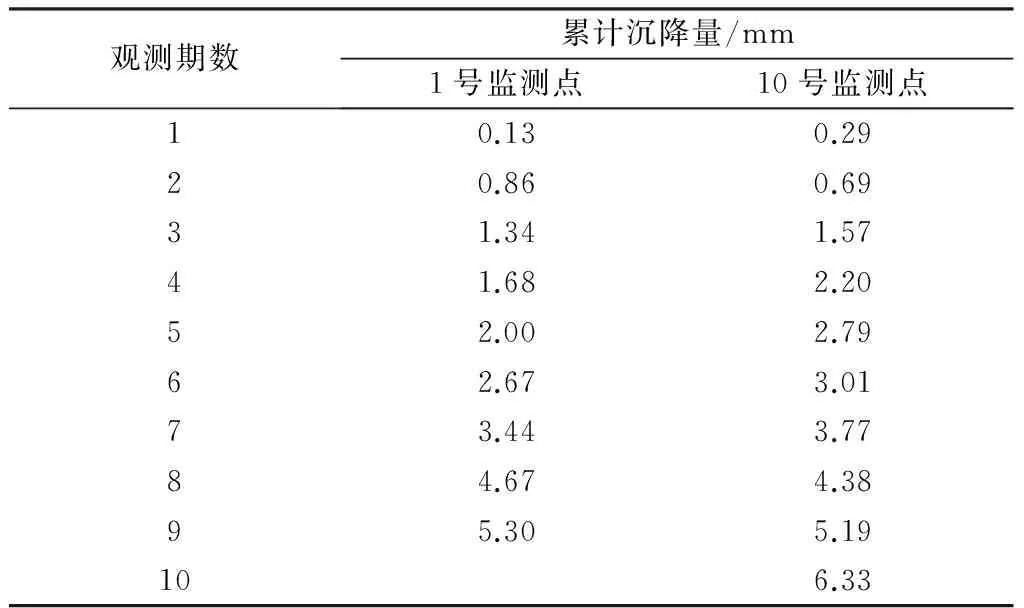
表2 1號和10號監測點的部分沉降觀測數據

據此分別建立4種模型，比較其預測效果。

(1) 模型1：GM(1,1)模型；

(2) 模型2：新陳代謝GM(1,1)模型；

(3) 模型3：優化初始值的GM(1,1)模型；

(4) 模型4：優化初始值的新陳代謝GM(1,1)模型。

對于1號監測點，選取1～9期觀測值為原始觀測數據建立模型，對10～13期進行預測；對于10號監測點，選取1～10期沉降觀測數據建立模型，對11～15期進行預測。預測結果如表3,4。

表3 4種模型預測結果及精度檢驗(1號監測點)

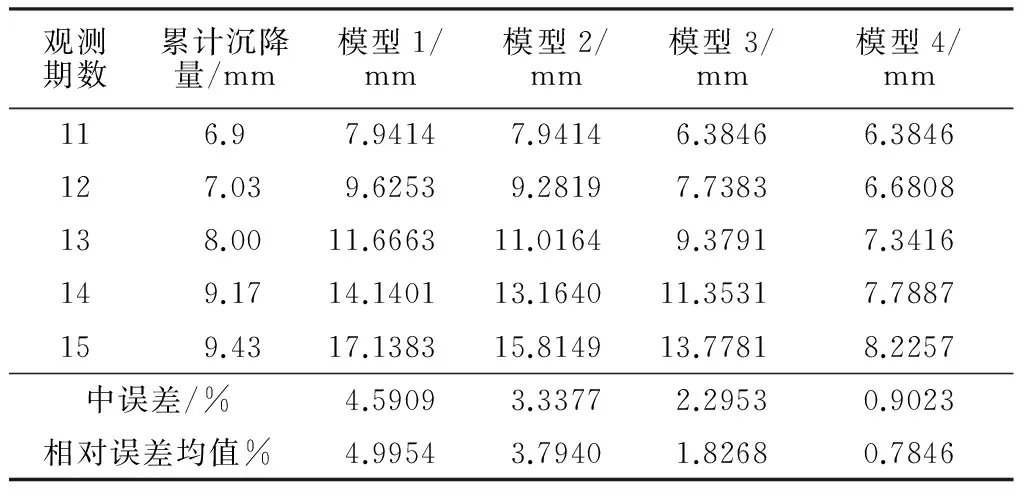
表4 4種模型預測結果及精度檢驗(10號監測點)

比較幾種模型的預測結果，GM(1,1)模型(模型1)預測精度最低，新陳代謝GM(1,1)模型(模型2)和基于優化初始值的GM(1,1)模型(模型3)比原始灰色模型的精度都要高。但是隨著時間的推移，預測的精度也越來越低。主要是因為變形沒有延續前期的增長趨勢。而基于優化初始值的新陳代謝模型(模型4)最優，預測值與實測值更加吻合，精度明顯提高。這是因為改正積分常數C能得到模型實測值與一階累加值的最佳擬合，且最新的數據包含了擾動因素的信息，加入到數據序列中進行預測，能更好地反映沉降變化趨勢的目前特征。

3 結 語

本文構建的基于優化初始值的新陳代謝GM(1，1)模型通過改正積分常數C，消除原點誤差，克服了傳統GM(1,1)模型以第一點作為初始值的缺陷，同時及時補充新數據，去掉因時間推移而使信息意義降低的老信息。選取初始條件和建模過程均為動態的，符合變形系統的演化特征，所以本文構建的模型精度明顯高于原始灰色模型、新陳代謝GM(1,1)模型和優化初始值的灰色系統，因此在基坑的變形監測數據分析中，應用基于優化初始值的新陳代謝GM(1,1)模型是行之有效的。

[1] 郭齊勝.系統建模原理與方法[M].長沙：國防科技大學出版社，2003.

[2] 黃聲享，尹暉，蔣征.變形監測數據處理[M].武漢：武漢大學出版社，2003.

[3] 邱淑芳，王澤方.灰色GM(1，1)模型背景值計算的改進[J].知識叢林，2007(2)：129-131.

[4] 鄧聚龍.灰色系統基本方法[M].武漢：華中理工大學出版社，1987.

[5] 周衛.基于MATLAB的灰色系統沉降預測[J].測繪通報，2002(6)：34-36.

[6] 王利，張雙成.動態灰色預測模型在大壩變形監測及預報中的應用研究.西安科技大學學報，2005,25(3):328-332.

[7] 劉棠洪. 殘差灰色預測模型在地面沉降監測中的應用[J]. 城市環境與城市生態，2007，20(5)：32-34.

(編輯：唐湘茜)

2017-03-31

江寶鋒，男，長江水利委員會水文局長江口水文水資源勘測局，工程師.

1006-0081(2017)06-0036-03

P258

A