鐵皮石斛新品種“仙斛3號(hào)”的選育及特征特性研究△
徐靖,王曉彤,胡凌娟,李明焱,邵清松,賈宸
(1.浙江壽仙谷醫(yī)藥股份有限公司,浙江 武義 321200;2.浙江省珍稀植物藥工程技術(shù)研究中心,浙江 武義 321200;3.金華壽仙谷藥業(yè)有限公司,浙江 武義 321200;4.浙江農(nóng)林大學(xué) 中藥學(xué)科,浙江 杭州 311300)
·專題·
鐵皮石斛新品種“仙斛3號(hào)”的選育及特征特性研究△
徐靖1,2*,王曉彤3,胡凌娟3,李明焱1,2,邵清松4,賈宸4
(1.浙江壽仙谷醫(yī)藥股份有限公司,浙江 武義 321200;2.浙江省珍稀植物藥工程技術(shù)研究中心,浙江 武義 321200;3.金華壽仙谷藥業(yè)有限公司,浙江 武義 321200;4.浙江農(nóng)林大學(xué) 中藥學(xué)科,浙江 杭州 311300)
目的:在以往研究工作基礎(chǔ)上,選育出鐵皮石斛優(yōu)良品種,促進(jìn)鐵皮石斛產(chǎn)業(yè)健康發(fā)展。方法:通過雜交、誘變、篩選等方法,選育出高產(chǎn)、優(yōu)質(zhì)的鐵皮石斛新品種。結(jié)果:獲得了適應(yīng)性及抗逆性強(qiáng)、產(chǎn)量高的鐵皮石斛新品種“仙斛3號(hào)”。與對(duì)照品種“新黑”、“仙斛1號(hào)”比較,“仙斛3號(hào)”新鮮莖葉、莖產(chǎn)量以及浸出物含量均顯著高于對(duì)照品種。SSR分子標(biāo)記分析表明“仙斛3號(hào)”與石斛屬其他品種(系)存在明顯遺傳差異。結(jié)論:“仙斛3號(hào)”是繼“仙斛2號(hào)”之后又一個(gè)鐵皮石斛新品種,為鐵皮石斛的合理開發(fā)利用與保護(hù)提供方向與依據(jù)。
鐵皮石斛;仙斛3號(hào);SSR標(biāo)記;選育;特征特性
鐵皮石斛DendrobiumofficinaleKimura et Migo 屬蘭科多年生附生草本植物,主要產(chǎn)于浙江、四川、云南、貴州等地[1]。《本草綱目》稱其具有“強(qiáng)陰益精,厚腸胃,補(bǔ)內(nèi)絕不足,長(zhǎng)肌肉,益智除驚,輕身延年”的作用[2]。但是鐵皮石斛自然繁殖率低,對(duì)環(huán)境要求較高,長(zhǎng)期以來遭受人類過度采集,其野生資源匱乏[3]。1987年國(guó)務(wù)院將鐵皮石斛列入野生藥材重點(diǎn)保護(hù)物種,禁止流通貿(mào)易,鐵皮石斛因此成為具極高附加值的非主要農(nóng)作物(中藥材)種類[4]。研究表明,鐵皮石斛中含有大量的多糖,具有較強(qiáng)的抗腫瘤和增強(qiáng)免疫力功能[5-7]。研究團(tuán)隊(duì)長(zhǎng)期以來從事鐵皮石斛種質(zhì)資源收集、評(píng)價(jià)、新品種選育工作,先后選育出“仙斛1號(hào)”、“仙斛2號(hào)”等鐵皮石斛新品種。本研究以“仙斛1號(hào)”(作父本)和“514”號(hào)”(作母本)雜交得到F1代蒴果進(jìn)行航天搭載,并對(duì)誘變蒴果進(jìn)行人工篩選,獲得了一個(gè)新的鐵皮石斛新品種“仙斛3號(hào)”,該品種于2016年1月通過了浙江省非主要農(nóng)作物審定,本文主要對(duì)該品種的特征特性進(jìn)行詳細(xì)的研究,以便為其更大范圍的推廣種植提供依據(jù)和參考。
1 材料與方法
1.1 供試材料
以“新黑”和本單位選育并通過認(rèn)定的“仙斛1號(hào)”為對(duì)照品種開展品比試驗(yàn)。“仙斛3號(hào)”為試驗(yàn)對(duì)象,其來源為2005~2008年以“仙斛1號(hào)”作為父本和“514號(hào)”為母本雜交得到的蒴果F1M514,經(jīng)航天搭載得到航天誘變蒴果H-F1M514,經(jīng)無菌播種、組織培養(yǎng)、篩選所得(見圖1)。

圖1 “仙斛3號(hào)”植株
1.2 試驗(yàn)材料擴(kuò)繁及栽培
參照李明焱等[2]研究報(bào)道,組織培養(yǎng)采用改良的MS培養(yǎng)基,以莖段和種子為組織培養(yǎng)外植體。4~6月份移栽組培苗,以食用菌廢料、木屑、石粉、菜餅等按一定比例混合、發(fā)酵為栽培基質(zhì),采用叢栽方法,每叢3~4株苗,行距為20 cm×15 cm,移栽后加強(qiáng)濕度控制,促進(jìn)根部生長(zhǎng),提高成活率。同時(shí)加強(qiáng)棚內(nèi)溫度、濕度、光照、空氣、基質(zhì)含水量及病蟲害的管理,促其正常生長(zhǎng)。
1.3 品比試驗(yàn)
以“新黑”和“仙斛1號(hào)”作為對(duì)照品種,在杭州(浙江中信藥用植物種業(yè)有限公司杭州基地)、建德(杭州小香生態(tài)農(nóng)業(yè)科技有限公司建德基地)、武義(金華壽仙谷藥業(yè)有限公司源口種植基地)各設(shè)一個(gè)試驗(yàn)點(diǎn),每個(gè)點(diǎn)重復(fù)3小區(qū),每小區(qū)面積9 m2。移栽定植后,分別隔12個(gè)月、24個(gè)月、36個(gè)月,從每小區(qū)隨機(jī)取3叢鐵皮石斛用于測(cè)定產(chǎn)量、灰分、浸出物、峰面積比和石斛多糖、甘露糖含量。產(chǎn)量測(cè)定時(shí),比較新鮮莖葉產(chǎn)量,同時(shí)去葉比較新鮮莖的產(chǎn)量。石斛多糖含量測(cè)定參照《中華人民共和國(guó)藥典》方法[8],計(jì)算干品多糖百分率。
1.4 顯微結(jié)構(gòu)分析
以“仙斛3號(hào)”新鮮莖、葉為材料,采用石蠟切片技術(shù)制作植物組織切片;新鮮的葉鞘制備成水封片。采用固綠和番紅染色,中性樹膠封片,然后在高倍顯微鏡下進(jìn)行顯微結(jié)構(gòu)觀察并攝像。
1.5 SSR分子標(biāo)記
為鑒別“仙斛3號(hào)”與其他鐵皮石斛在DNA水平上的差異,采用SSR分子標(biāo)記技術(shù)進(jìn)行了分析。選用“仙斛3號(hào)”及其他13種石斛屬的新鮮嫩葉為實(shí)驗(yàn)材料,采用QIAGENE提取試劑盒從葉片中提取DNA。PCR結(jié)果應(yīng)用Quantity one軟件進(jìn)行分析。
2 結(jié)果與分析
2.1 “仙斛3號(hào)”的植物學(xué)形態(tài)特征
“仙斛3 號(hào)”莖圓柱形,長(zhǎng)約8~21 cm,粗約2~6 mm,不分枝,具多節(jié),節(jié)間長(zhǎng)約0.8~1.4 cm,常在中部以上互生6~12枚葉。質(zhì)地堅(jiān)脆,易折斷,斷面綠色,呈細(xì)顆粒黏質(zhì)狀物。葉片稍帶肉質(zhì),長(zhǎng)圓狀披針形,長(zhǎng)約2~7 cm,寬約0.8~2.2 cm,先端鈍并且在葉尖部鉤轉(zhuǎn),基部下延為抱莖的鞘,邊緣和中肋常帶紫色斑點(diǎn)。葉鞘初生時(shí)與莖包裹嚴(yán)密,老時(shí)其上緣與莖松離而張開,變?yōu)榛野咨べ|(zhì),棱條更明顯,紫色斑點(diǎn)漸褪去。有時(shí)葉鞘頂部邊緣可超出上一莖節(jié)。總狀花序生于落了葉的老莖上部,具3~5朵花,花序軸長(zhǎng)約4~6 cm,稍回折狀彎曲。唇瓣黃白色,基部具1個(gè)綠色或黃色的胼胝體,卵狀披針形,比萼片稍短,中部反折,先端急尖,不明顯3裂,中部以下兩側(cè)具紫紅色條紋;唇盤密布細(xì)乳突狀的毛,并且在中部以上具1個(gè)紫紅色斑點(diǎn)。
2.2 “仙斛3號(hào)”的產(chǎn)量及品質(zhì)表現(xiàn)
2011—2013年,在浙江杭州市、建德市、武義縣3地進(jìn)行了兩輪連續(xù)3年的品種比較試驗(yàn),分別測(cè)定了移栽后12個(gè)月、24個(gè)月、36個(gè)月的新鮮莖葉產(chǎn)量。結(jié)果表明,“仙斛3號(hào)”12個(gè)月3地兩輪平均新鮮莖葉產(chǎn)量為0.659 kg·m-2,比對(duì)照品種“新黑”和“仙斛1號(hào)”分別增產(chǎn)52.10%和 20.91%;24個(gè)月3地兩輪平均新鮮莖葉生長(zhǎng)量為2.515 kg·m-2,比對(duì)照品種“新黑”和“仙斛1號(hào)”分別增產(chǎn)65.57%和17.74%;36個(gè)月3地兩輪平均新鮮莖葉生長(zhǎng)量為3.205 kg·m-2,比對(duì)照品種“新黑”和“仙斛1號(hào)”分別增產(chǎn)50.33%和26.80%,且均顯著高于對(duì)照品種“新黑”和“仙斛1號(hào)”,見表1。
在實(shí)驗(yàn)中通過匯總灰分、浸出物、多糖、甘露糖、峰面積比來比較“仙斛3號(hào)”與對(duì)照品種品質(zhì)的區(qū)別。結(jié)果表明,“仙斛3號(hào)”灰分和甘露醇均顯著高于對(duì)照品種“新黑”和“仙斛1號(hào)”;“仙斛3號(hào)”灰分兩輪平均為5.346%,較“新黑”和“仙斛1號(hào)”分別增加16.73%和26.84%。浸出物兩輪平均為13.845%,較“新黑”和“仙斛1號(hào)”分別增加58.43%和67.47%。多糖和甘露糖含量均顯著低于對(duì)照品種“新黑”和“仙斛1號(hào)”。多糖含量?jī)奢喥骄鶠?3.410%,較“新黑”和“仙斛1號(hào)”分別減少18.65%和10.4%。甘露醇含量?jī)奢喥骄鶠?1.753%,較“新黑”和“仙斛1號(hào)”分別減少29.54%和16.06%。兩輪三地試驗(yàn)結(jié)果表明,“仙斛3號(hào)”各項(xiàng)品質(zhì)指標(biāo)均符合《中華人民共和國(guó)藥典》要求,見表2。
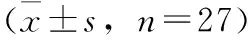
表1 “仙斛3號(hào)”與“新黑”和“仙斛1號(hào)”鮮品產(chǎn)量比較 kg·m-2
注:相同小寫字母表示同列數(shù)據(jù)無統(tǒng)計(jì)學(xué)差異(P>0.05);不同小寫字母表示同列數(shù)據(jù)有統(tǒng)計(jì)學(xué)差異(P<0.05);下同。

表2 “仙斛3號(hào)”與對(duì)照品種品質(zhì)比較
2.3 “仙斛3號(hào)”的顯微結(jié)構(gòu)
莖切片結(jié)果顯示:1)表皮細(xì)胞由1列細(xì)胞組成,扁平,外被黃色角質(zhì)層,邊緣呈不規(guī)則波狀。每2個(gè)波狀中夾有一個(gè)深波狀彎曲,外層可見無色的薄壁細(xì)胞組成的葉鞘層。2)基本薄壁組織細(xì)胞呈多角形,大小不一,占據(jù)莖橫切面的絕大部分,薄壁細(xì)胞長(zhǎng)約23~85 μm,寬約7~47 μm,多數(shù)維管束散在其間。3)維管束為有限外韌型,維管束橫截面面積約為3850 μm2,略排成3~5圈,其中纖維細(xì)胞直徑約為4~6 μm。見圖2。
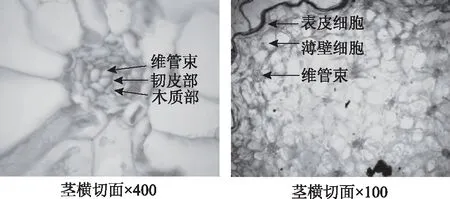
圖2 “仙斛3號(hào)”莖橫切面石蠟切片顯微結(jié)構(gòu)圖
葉鞘顯微鑒定結(jié)果:葉上表皮排列緊密,多角形,壁薄,增厚不明顯;上表皮細(xì)胞長(zhǎng)約為56~81 μm、寬約為45~48 μm。上表皮無氣孔(見圖3A、3B)。下表皮排列緊密,長(zhǎng)方形,呈行排列,壁增厚;下表皮細(xì)胞長(zhǎng)約為30~66 μm、寬約為12~29 μm;氣孔分布松散,呈腎形,在230~470 μm2面積內(nèi)分布3個(gè)氣孔,氣孔長(zhǎng)度約為24 μm、寬度約為16 μm,氣孔指數(shù)為16%(見圖3C、3D)。葉鞘細(xì)胞排列緊密不規(guī)則,形狀多種,增厚不明顯;可見紫色斑點(diǎn),成群散列分布。葉鞘細(xì)胞長(zhǎng)度約為21~40 μm,寬約為19~30 μm(見圖3E、3F)。

注:A.葉上表皮(×100);B.葉上表皮(×400);C.葉下表皮(×100);D.葉下表皮(×400);E.葉鞘細(xì)胞(×100);F.葉鞘細(xì)胞(×200)。圖3 “仙斛3號(hào)”葉及葉鞘水封片顯微結(jié)構(gòu)圖
2.4 “仙斛3號(hào)”與其他鐵皮石斛的SSR分子標(biāo)記分析
采用QIAGENE提取試劑盒從葉片中提取DNA,采用穩(wěn)定性高、重復(fù)性好、共顯性的SSR分子標(biāo)記方法,從公開發(fā)表的鐵皮石斛基因組特異的SSR 分子標(biāo)記中進(jìn)行篩選。經(jīng)過篩選,獲得可以完全區(qū)分“仙斛3號(hào)”的3個(gè)多態(tài)性條帶豐富的SSR分子標(biāo)記:OA15、XML003和XML006(見表3)。結(jié)果表明,采用OA15和XML003兩個(gè)分子標(biāo)記能夠?qū)ⅰ跋甚? 號(hào)”(編號(hào)1)與其他樣品區(qū)分開,而其他樣品之間的差異可以從OA15、XML003、XML006 3個(gè)分子標(biāo)記中區(qū)分(見圖4)。從帶型分析,OA15基本上可以將“仙斛3號(hào)”與石斛屬的其他種區(qū)分開。因此,從這兩個(gè)SSR分子標(biāo)記的PCR結(jié)果可以看出“仙斛3號(hào)”在遺傳上具有特異性,區(qū)別于石斛屬的其他種。

表3 區(qū)分“仙斛3號(hào)”與其他13份石斛屬材料的SSR分子標(biāo)記

注:A.OA15;B.XML003;C.XML006;M.Marker。圖4 “仙斛 3 號(hào)”及其他13份石斛屬材料SSR分子標(biāo)記分析
3 討論
野生鐵皮石斛由于生長(zhǎng)條件苛刻,自然產(chǎn)量極為稀少,更因民間長(zhǎng)期過度采挖,致使野生資源瀕臨絕種。我國(guó)目前的石斛栽培生產(chǎn)仍然處于起步階段,產(chǎn)業(yè)發(fā)展前景十分廣闊[2]。“仙斛3號(hào)”是繼“仙斛1號(hào)”后選育的第3個(gè)鐵皮石斛品種。從品種比較試驗(yàn)可以看出,“仙斛3號(hào)”具有高產(chǎn)、優(yōu)質(zhì)、生長(zhǎng)迅速等特點(diǎn);綜合性狀與“新黑”和“仙斛1號(hào)”有明顯差異;在產(chǎn)量上,明顯優(yōu)于“仙斛1號(hào)”;其干品石斛多糖和甘露糖含量要低于“新黑”和“仙斛1號(hào)”。鐵皮石斛的品質(zhì)指標(biāo)目前主要按照《中華人民共和國(guó)藥典》的要求,比較多糖和甘露糖含量,“仙斛3號(hào)”多糖和甘露糖的含量均符合《中華人民共和國(guó)藥典》規(guī)定[8]。顯微結(jié)構(gòu)鑒定是生物學(xué)鑒定的常用手段,本研究的顯微結(jié)構(gòu)鑒定與文獻(xiàn)描述一致,可以認(rèn)為“仙斛3號(hào)”具有鐵皮石斛典型結(jié)構(gòu)特征。PCR結(jié)果可以看出“仙斛3號(hào)”在遺傳上具有特異性,區(qū)別于石斛屬的其他種。“仙斛3號(hào)”的培育,對(duì)鐵皮石斛在健康產(chǎn)業(yè)方面的發(fā)展,具有重大的推動(dòng)意義,它為鐵皮石斛種植提供了更多的選擇,同時(shí)為石斛產(chǎn)業(yè)提供了品質(zhì)的保證。
[1] 謝偉杰,張永萍,徐劍,等.鐵皮石斛現(xiàn)代研究進(jìn)展[J].現(xiàn)代中醫(yī)藥,2016,36(4):87-91.
[2] 李明焱,謝小波,朱惠照,等.鐵皮石斛新品種“仙斛1號(hào)”的選育及其特征特性研究[J].中國(guó)現(xiàn)代應(yīng)用藥學(xué),2011,28(4):281-284.
[3] 白音,包英華,金家興,等.我國(guó)藥用石斛資源調(diào)查研究[J].中草藥,2006,37(9):4-5.
[4] 順慶生.中藥石斛的新資源——齒瓣石斛(紫皮)[J].中國(guó)現(xiàn)代中藥,2011,13(11):23-24.
[5] Chen X M,Wang C L,Wang A R,et al.Study on polysaccharides in Dendrobium officinale protocorm[J].Chinese Pharmaceutical Journal,2011,46(20):1552-1556.
[6] 李明焱,王瑛,鄭化先,等.鐵皮石斛新品種“仙斛2號(hào)”的選育和特征特性研究[J].中國(guó)藥學(xué)雜志,2013,48(19):1677-1680.
[7] 羅宇琴,肖蘇萍,趙潤(rùn)懷,等.霍山石斛與鐵皮石斛對(duì)比研究進(jìn)展[J].中國(guó)現(xiàn)代中藥,2016,18(8):1067-1070.
[8] 國(guó)家藥典委員會(huì).中華人民共和國(guó)藥典:一部[S].北京:中國(guó)醫(yī)藥科技出版社,2015:282-283.
BreedingofDendrobiumofficinalevar.“Xianhu3”andItsCharacteristics
XUJing1,2*,WANGXiaotong3,HULingjuan3,LIMingyan1,2,SHAOQingsong4,JIAChen4
(1.ZhejiangShouxianguPharmaceuticalCo.Ltd,Wuyi321200,China;2.ZhejiangEngineeringResearchCenterofRarePlantMedicine,Wuyi321200,China;3.JinhuaShouxianguPharmaceuticalCo.Ltd.,Wuyi321200,China;4.DepartmentofTraditionalChineseMedicine,ZhejiangA&FUniversity,Hangzhou311300,China)
Objective:To select and breed elite variety ofDendrobiumofficinaleon the basis of previous research work,thus to promote the healthy developing ofD.officinaleindustry.Methods:Hybridization,mutagenesis,screening etc.was employed for the breeding of high yeild and high quality,new variety developedD.officinale.Results:The adaptability and strong resistance,Dendrobiumnew varieties of high yield “Xianhu 3 ”.Compared with the control variety “Xinhei”,“Xianhu 1”,“Xianhu 3 ” fresh stem leaf,stem yield and extract content were significantly higher than that of CK.SSR molecular marker analysis showed that “Xianhu 3 ” and other species ofDendrobium(lines) have obvious genetic differences.Conclusion:“Xianhu 3 ” was a new elite variety ofDendrobiumvarieties with the following of “Xianhu 2 ”.Its breeding provided direction and basis forD.officinalereasonable development and utilization and protection.
Dendrobiumofficinale;Xianhu 3;SSR marker;breeding;characteristics
2017-01-16)
浙江省中藥材新品種選育重大科技專項(xiàng)(2016C02058);浙江省重點(diǎn)研發(fā)計(jì)劃項(xiàng)目(2017C02011)
*
徐靖,工程師,研究方向:藥用植物栽培與育種;Tel:(0579)87980003,E-mail:37117894@qq.com
10.13313/j.issn.1673-4890.2017.3.007

