數據流中ρ-支配輪廓查詢算法*

2017-07-31 20:55:55王之瓊霸建民信俊昌

計算機與生活 2017年7期

關鍵詞：定義

王之瓊，霸建民，黃達，信俊昌+

1.東北大學中荷生物醫學與信息工程學院，沈陽 110819

2.東北大學計算機科學與工程學院，沈陽 110819

數據流中ρ-支配輪廓查詢算法*

王之瓊1，霸建民2，黃達2，信俊昌2+

1.東北大學中荷生物醫學與信息工程學院，沈陽 110819

2.東北大學計算機科學與工程學院，沈陽 110819

+Corresponding autho author:r:E-mail:xinjunchang@mail.neu.edu.cn

WANG Zhiqiong,BA Jianm in,HUANG Da,etal.ρ-dom inant skyline com putation on data stream s.Journal of Frontiersof Computer Scienceand Technology,2017,11(7)：1080-1091.

數據流上的輪廓查詢算法不能直接處理ρ-支配輪廓查詢，而傳統的ρ-支配輪廓查詢無法在數據更新頻繁時滿足查詢處理的實時性需求。因此，提出了數據流上的ρ-支配輪廓查詢算法。首先，系統地介紹了完全支配、ρ-支配和ρ-支配輪廓的定義，進而提出了數據流上ρ-支配輪廓的定義。然后，通過深入分析數據流上的ρ-支配輪廓的性質，得出基于時序支配的數據過濾方法，并提出了基于滑動窗口的ρ-支配輪廓查詢算法（ρ-dominant skyline query over sliding w indow，DSSW），提高了數據流上的ρ-支配輪廓計算的效率。最后，通過大量的實驗證明，DSSW算法相比較于傳統的ρ-支配輪廓查詢算法，在響應時間及存儲空間上均有明顯優勢。

ρ-支配關系；ρ-支配輪廓；數據流；滑動窗口

1 引言

近年來，輪廓查詢[1-3]被廣泛地應用于多標準決策中，例如個性化推薦系統、市場監測系統等。給定一個數據點集合P，則數據集P的輪廓是指P中所有不被其他點支配的點的集合。需要指出的是一個點x支配另一個點y必須滿足x在所有維上都不比y差，并且至少在一維上x比y好。不失一般性，假設一個小的值比大的值好，在d維數據空間內，點x支配y可以表示為：（1）?i∈[1,d],x[i]≤y[i]；（2）?j∈[1,d],x[j]＜y[j]。圖1（a）中的點a、f和g由于不被其他任何點支配，就構成了圖1（a）的輪廓。

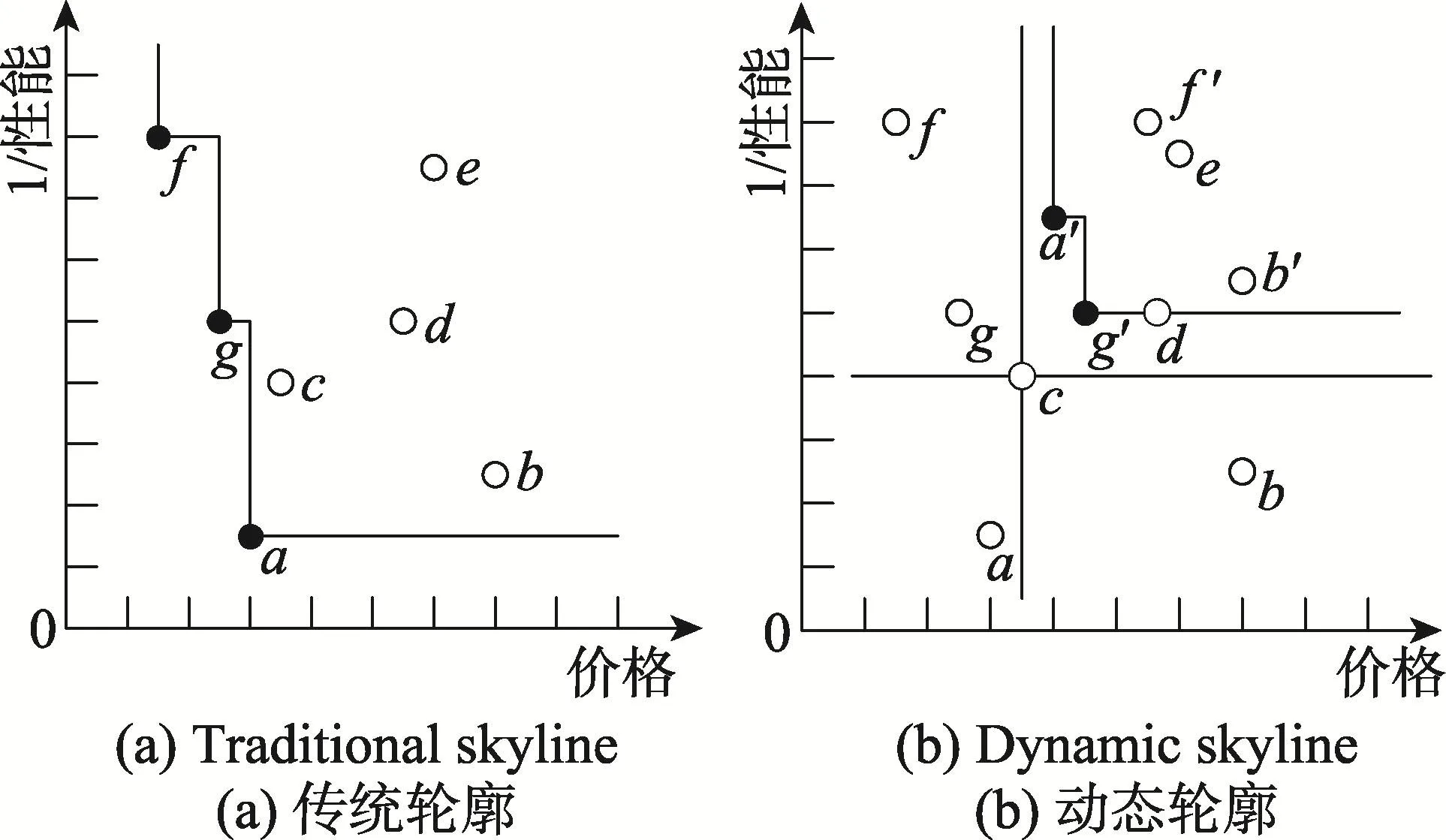
Fig.1 Exampleof traditionalskylineand dynamic skyline圖1 傳統輪廓與動態輪廓示例圖

動態輪廓[4]為傳統輪廓的一種變體，致力于在查詢點的變換空間中計算輪廓。給定一個d維空間內查詢點q，則對于任意一個d維數據p，都可以關于查詢點q變換為p′，并且p′滿足p′[i]=|p[i]-q[i]|+q[i],i∈[1,d]。圖1（b）是圖1（a）中以c為查詢點的動態輪廓結果，因為點a′和g′在變換空間中不被其他任何點支配，所以點a′和g′構成了此集合的動態輪廓。動態輪廓比傳統的輪廓有更廣泛的應用，例如在一個電商平臺中，如果一個消費者感興趣的商品已售空，則電商平臺可將與之類似的商品推薦給消費者。相當于以已售空的商品作為查詢點，將動態輪廓計算結果推薦給消費者。

由于電商平臺的商品數量巨大，通過動態輪廓查詢后，推薦給消費者的商品數量仍然很多，無法幫助消費者進行選擇，可通過ρ-支配輪廓查詢解決，通過調節ρ值的大小完成對輪廓集大小的控制，從而實現向消費者推薦其期望的商品數量。

然而，電商數據具有典型的數據流特點。傳統的ρ-支配輪廓查詢不能滿足具有無限性和實時性的數據流中的查詢需求，因而本文將研究數據流中的ρ-支配輪廓查詢來滿足此類現實應用。平臺中商品的更新是頻繁的，則很久以前的商品成為推薦商品的概率極小，因此可以只關注最近一段時間內平臺中的商品。本文在基于append-only數據流的基礎上應用滑動窗口來研究數據流中的ρ-支配輪廓查詢算法。

首先，給出了完全支配關系、ρ-支配關系、ρ-支配輪廓和數據流上ρ-支配輪廓的定義。然后，深入地分析了數據流上ρ-支配輪廓的性質，建立了基于時序支配的數據過濾方法，并據此提出了基于滑動窗口的ρ-支配輪廓查詢算法（ρ-dom inant skyline query over sliding w indow，DSSW）。最后，通過實驗證明DSSW算法提高了數據流上的ρ-支配輪廓計算的效率。

2 相關工作

2.1 輪廓查詢

一些學者針對非數據流上的輪廓查詢進行了大量的研究工作。Borzsonyi等人[1]提出了嵌套循環算法，將某個元組p與其他元組逐一比較，如果p不被任意其他元組支配，則p是輪廓點，并使用輪廓操作去擴展數據庫系統；Papadias等人[2]提出了基于最近搜索的BBS（branch-and-bound skyline）算法，此算法僅僅對可能包含輪廓點的R樹節點執行一次存取并且不進行重復檢索，另外此算法還可以有效地應用于各種變體輪廓查詢中；Chen等人[3]提出了定義在動態空間中的動態輪廓查詢，通過動態索引給出了一種有效的剪枝技術去計算動態輪廓，并且論證了剪枝后動態輪廓查詢的性能；Chan等人[4]提出了考慮不同維度時多久返回輪廓結果的頻率輪廓查詢，并應用找出top-k頻率的輪廓點給出了一種計算方法；Yiu等人[5]應用多維數據索引和深入探究top-k支配的特點給出了一種計算top-k輪廓的算法；Chen等人[6]通過大量的無組織的分布式環境研究了約束輪廓，首先利用一種分割算法將所有的數據分割為一些群組以便可以并發處理這些數據，然后提出了一個并行處理算法。

也有學者針對數據流上的輪廓查詢開展了一些研究工作。Kossmann等人[7]第一次提出了持續的輪廓查詢算法，首先立刻返回一組輪廓，然后持續不斷地返回多組輪廓并且允許使用者控制計算時間；Lin等人[8]第一次提出了在最近N組數據中計算輪廓的n-of-N輪廓查詢，提出了一種剪枝技術和一種高效數據存取技術，并且提出了一種持續計算n-of-N輪廓的算法；Zhang等人[9]分析了需要保存數據的特點和輪廓集合的大小，提出了不確定數據流上的輪廓查詢算法；Ding等人[10]研究了不確定數據流上的輪廓查詢問題；Yang等人[11]提出了DC-Tree算法去計算數據流上的輪廓查詢；Zhu等人[12]提出了以DC-tree作為索引的反輪廓查詢算法，并且應用剪枝技術縮減了查找空間的大小；Bai等人[13]提出了不確定數據流上概率反輪廓查詢的定義以及索引模型，并且提出了一種基于R-tree的不確定數據流上的反輪廓查詢算法（probabilistic reverse skyline on uncertain data streams based on R-tree index，RT2RS）；Dellis等人[14]采用多個低維索引來支持任意子空間的限制性輪廓查詢；Morse等人[15]提出了LookOut算法來計算連續時間間隔的輪廓查詢。

2.2 ρ-支配輪廓查詢

2011年，Xin等人[16]首先提出了基于數值間比例值大小的ρ-支配關系和ρ-支配輪廓查詢的概念，并建立了一種應用于傳統數據集上的基于分支定界的ρ-支配輪廓查詢算法（branch and boundρ-dominant skyline algorithm，BBDS）。BBDS算法采用標準的R樹索引存儲數據，并將所有數據分為兩類：ρ-支配輪廓集合S和非ρ-支配輪廓集合SS，初始時兩集合均為空。采用廣度優先遍歷算法遍歷R樹中的節點e，如果e是中間節點，判斷e是否被S+SS中的兩個數據支配；若不被兩個數據支配，則遍歷所有不被兩個元素支配的子節點。如果e是葉子節點，判斷e是否被S+SS中的數據支配，如果不被支配，繼續判斷是否被S+SS中的數據ρ-支配，若不被ρ-支配則將e加入到S中，否則將e加入到SS中；接著將S中被eρ-支配的集合加入到SS中。

但是在數據流中，若每當有數據更新時便先維護R樹，再調用BBDS算法，必將花費大量的時間和空間代價。總之，傳統的ρ-支配輪廓查詢無法在數據更新頻繁時滿足查詢處理的實時性需求，而數據流上的輪廓查詢不能滿足數值間比例關系的輪廓查詢。因此，本文將深入研究數據流中的ρ-支配輪廓查詢問題。

3 問題描述

首先回顧完全支配關系和ρ-支配關系[16]的定義。

圖2（a）顯示了二維空間中完全支配的一個例子。因為對任意一維b和q之間的距離比a和q之間的距離短，并且a、b在q的同一側，所以點b關于查詢點q完全支配點a。同理，點h關于查詢點q完全支配點g。而點b、c、d、e、f和點h不被其他任一點完全支配。

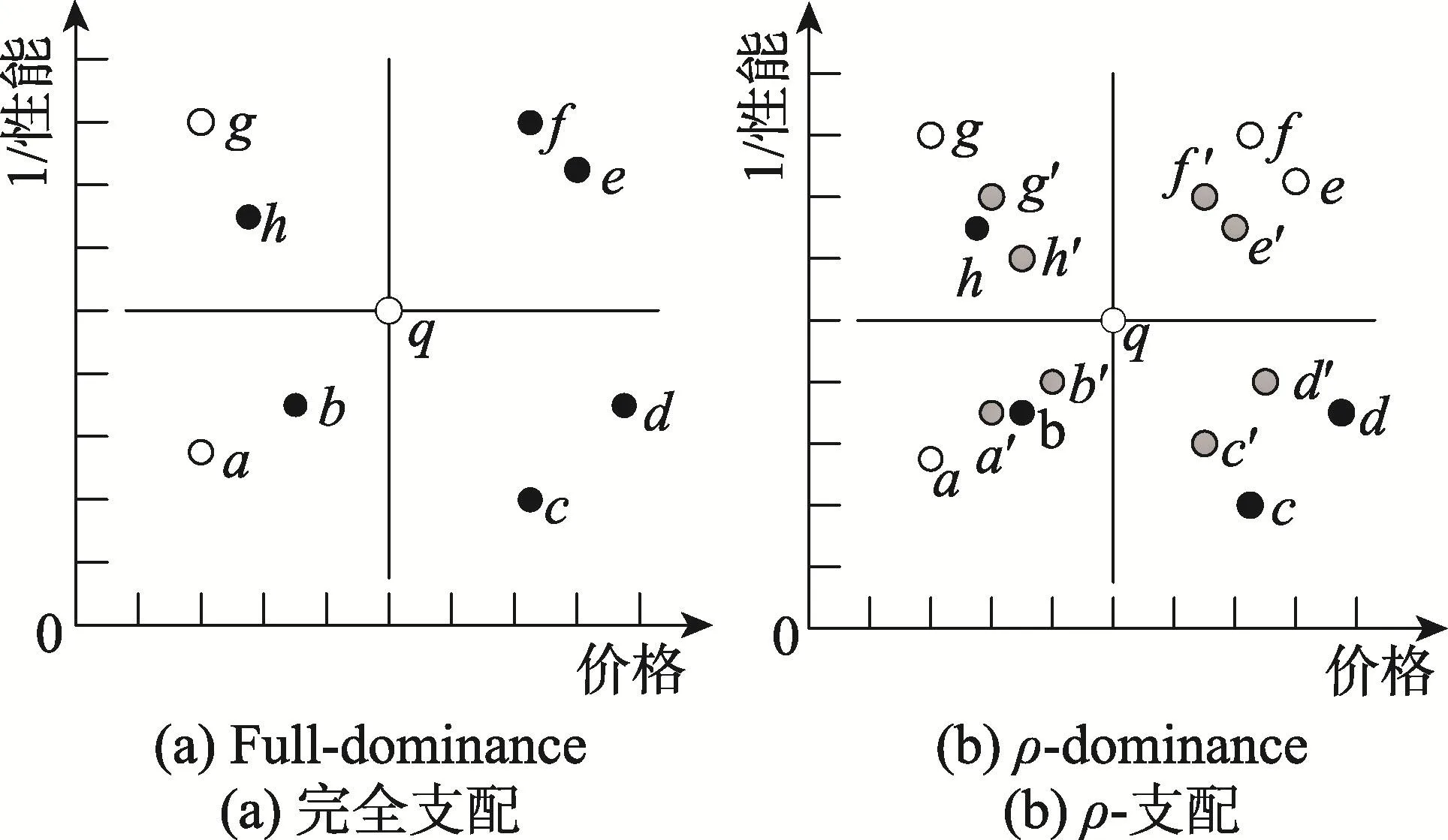
Fig.2 Example of full-dom inance andρ-dom inance圖2 完全支配和ρ-支配示例圖

圖2（b）展示了當ρ取值為1.5時的ρ-支配關系的例子，在本例中使用x′表示x與q的1/3分位點。因為對任意一維點b′和點q之間的距離比點a和點q之間的距離小，并且b′和a在點q的同一側，所以點b關于查詢點q1.5-支配點a。同理可得，點f關于查詢點q1.5-支配點e，并且點e關于查詢點q1.5-支配點f，點h關于查詢點q1.5-支配點g。而點b、c、d和h不被其他任意點1.5-支配。

由完全支配關系和ρ-支配關系可以容易地得出完全支配輪廓和ρ-支配輪廓[16]的定義，如定義3和定義4所示。

定義3（完全支配輪廓）給定一個數據集合P和一個查詢點q，數據集P中所有不被P中其他點關于點q完全支配的點構成數據集P的完全支配輪廓。

定義4（ρ-支配輪廓）給定一個數據集合P和一個查詢點q，數據集P中所有不被P中其他點關于點qρ-支配的點構成數據集P的ρ-支配輪廓。

根據定義3可得，如果一個點p不被數據集中其他任一點關于查詢點q完全支配，則點p為一個完全支配輪廓點。如圖2（a）所示，點b、c、d、e、f和h不被其他任意點完全支配，因此點b、c、d、e、f和h構成了圖2（a）的完全支配輪廓。同理可以得出點b、c、d和h組成圖2（b）的1.5-支配輪廓。

根據定義3和定義4可以容易地看出完全支配輪廓是ρ-支配輪廓中ρ取值為1時的特例。

類似ρ-支配輪廓，可以得出數據流上的ρ-支配輪廓的定義。用PN表示數據流中最近的N組數據，即滑動窗口中的數據，并且用L(p)表示點p在數據流中的位置，L(p)大的點表示后到，數據流中的ρ-支配輪廓如定義5所示。

定義5（數據流中的ρ-支配輪廓）給定一個數據流P和一個查詢點q，則數據流上PN中不被其他任一點ρ-支配的點構成數據流P的ρ-支配輪廓。

4 數據流中的ρ-支配輪廓查詢

本文將詳細介紹DSSW算法，首先深入分析數據流上的ρ-支配輪廓的性質；接著根據數據流上ρ-支配輪廓的性質建立數據過濾方法；最后詳細地給出DSSW算法的具體過程。

4.1 ρ-支配輪廓的性質

當ρ小于等于1時，ρ-支配關系滿足傳遞性，因此ρ小于等于1時的ρ-支配輪廓可以采用類似于輪廓查詢的方式來計算，故本文只討論ρ大于1時的情況。

如圖2（a）和圖2（b）所示，對于同一個數據集合P，完全支配輪廓包含點b、c、d、e、f和h，而1.5-支配輪廓包含點b、c、d和h，從中可以容易地看出完全支配輪廓點包含1.5-支配輪廓點。此結論更一般的表達如定理1所示。

定理1給定兩個值ρ1和ρ2，并且ρ1＞ρ2，如果一個點 p是 ρ1-支配輪廓點，那么 p一定也是 ρ2-支配輪廓點。

由定理1可以看出，通過調節ρ值的大小可以控制結果集的大小，因此 ρ-支配輪廓查詢有更廣泛的應用。

定理2給定兩個點x和y，如果 ρ＞1并且x?qy，則

由定理2可以看出，如果一個點x被另一個點y完全支配，那么當 ρ＞1時點x也被點yρ-支配。由定理2的證明過程可以容易地得出反之不成立。

定理3給定數據流中的兩個點x和y，如果并且L(x)＞L(y)，則點y不可能成為 ρ-支配輪廓點。

證明因為，所以當x屬于PN時點y不是ρ-支配輪廓點。又由于在數據流中L(x)＞L(y)，則在PN中y比x先消失，從而y不可能成為一個 ρ-支配輪廓點。 □

引理1給定數據流中的兩個點x和y，如果x?qy并且L(x)＞L(y)，則點y不可能成為 ρ-支配輪廓點。

由定理2和定理3可以容易地證出引理1。

定理4如果x?qy和，那么

一個點p可能同時被PN中多個點ρ-支配，并且PN中只要存在一個 ρ-支配點 p的點，點 p就不是 ρ-支配輪廓點，因此點 p是否是 ρ-支配輪廓點將由 ρ-支配它的點中最后一個到達的點n是否存在于PN中所決定，并且將點n記為 pre(p)。

4.2 過濾方法

考慮圖3中的例子，其中點按照它們的字母表順序依次到達，并且 ρ值為2。假設點c剛剛到達滑動窗口，并且滑動窗口的大小大于3，因為點a被點b2-支配，所以點a不可能成為ρ-支配輪廓點，但是如果將a過濾掉，因為點b不能 ρ-支配點c，所以點c將被判斷為 ρ-支配輪廓點。然而，從圖3中可以看出點aρ-支配點c，因此點c不是 ρ-支配輪廓點，不能直接將不可能成為ρ-支配輪廓點的點過濾掉。

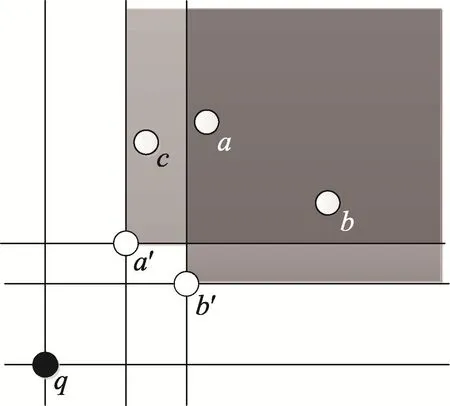
Fig.3 Counterexampleof filtering圖3 過濾的反例

如果一個點y被另一個后到的點x完全支配，根據定理4可得，則被點yρ-支配的點也被點xρ-支配，因此當刪除點y時，如果有新的被點yρ-支配的點z到達時，點z必將被點xρ-支配，從而不會影響點z是否成為 ρ-支配輪廓點；又根據引理1可得，點y不可能成為一個ρ-支配輪廓點，因此在輪廓計算前可以過濾掉被后到的點完全支配的點。

用SN表示PN中過濾后的點的集合，則SN={p|p∈PN,?/p′∈PN,L(p′)＞L(p)∧p′?qp}。進一步可以將SN劃分為3類：

（1）ρ-支配輪廓點(DN)，SN中不被其他任何點ρ-支配的點的集合；

（2）候選點(CN)，SN中被先到的點ρ-支配而不被后到的點ρ-支配的點的集合；

（3）輔助點(AN)，SN中被后到的點ρ-支配而不被后到的點完全支配的點的集合。

繼續考慮圖2（b）的例子，假設滑動窗口的大小不小于8，并且點按照字母表順序到達。因為點a和g分別被b和h完全支配，所以計算前過濾掉a和g，從而SN={b,c,d,e,f,h}；因為點b、c、d和h不被其他任一點ρ-支配，所以ρ-支配輪廓DN={b,c,d,h}；因為點f被一個先到的點eρ-支配而不被后到的點ρ-支配，所以候選點CN={f}；因為點e被一個后到的點ρ-支配而不被后到的點完全支配，所以輔助點AN={e}。

至此，已經建立了數據流中ρ-支配輪廓查詢的過濾方法。根據點集合的劃分方式可知一個新到達的點要么屬于DN，要么屬于CN。由過濾方法可得SN為計算ρ-支配輪廓所需要存儲的最小數據集合。

4.3 查詢過程

由定義1和定義2可以得出，完全支配關系和ρ-支配關系只能存在于查詢點同一側區域中的兩個點之間，因此當滑動窗口中一個新的點到達時只需判斷該點同一區域內的點與該點的支配關系（如果一個點與查詢點在某幾維上相同，則該點屬于多個區域）。在Xin等人[16]的算法中采用了R樹索引存儲方式，將SN中數據分配到2d個區域進行存儲。

盡管傳統的R樹索引存儲可以大大減少數據查找的時間消耗，但是當數據流中的數據更新時，刪除和插入等操作將花費大量的維護時間，降低了算法的時間效率。本文將使用2d個Map容器對SN中的數據進行存儲，當有新的數據更新時只需計算該數據所屬的區域R()并存儲即可。此方法既加快了數據查找時的效率，又省去了當數據更新時維護R樹所需的時間。

算法1描述了DSSW算法的具體查詢過程。當n個新的點p1-pn到達時，如果滑動窗口已滿，則查找滑動窗口中最先到達的n個點o1-on，并計算點所屬的區域R()，然后將點o1-on在相應的R()中刪除，并且在CN中查找被o1-on中的點ρ-支配的點的集合DC，將DC中的點從CN中轉移到DN中；計算出點p1-pn所屬的區域R()，并根據R()將p1-pn分成k組；對于k組中的每一組，在區域R()中查找被p1-pn中的點完全支配的點的集合DF，并且將這些點在PN中刪除，然后在R()中查找被p1-pn中的點ρ-支配的點的集合DS，并且將DS中的點從DN和CN中移到AN；如果在區域R(pi)中存在點zρ-支配點pi，將點pi加入到CN中，否則將點pi加入到DN中；最后將點pi存儲到區域R(pi)中。

算法1DSSW算法

1.while（新的n個點p1-pn到達）

2.if（滑動窗口已滿）

3.查找最先進入窗口的n個點o1-on

4.分別計算點o1-on的區域R()

5.將o1-on分別在所在的區域R()中刪除

6.在CN中查找以o1-on中的點為pre()的集合DC

7.將DC從CN移動到DN

8.計算點p1-pn的區域R()

9.將p1-pn按照所在的區域R()分成k組

10.for（k組中的每一組）

11.在本區域R()中查找被p1-pn中的點完全支配的集合DF

12.將DF中的點過濾掉

13.在本區域R()中查找被點p1-pn中的點ρ-支配的集合DS

14.將DS中的點從DN和CN移動到AN

15. for（p從p1-pn）

16. if（存在點z為pre(p)）

17.pre(p)=L(z)

18.將點p加入集合CN

19. else

20.將點p加入集合DN

21.將點p存儲到相應的R(p)中

算法2描述了點p所屬區域的計算過程。在此過程中，假設點p和查詢點q都是d維。如果在第一維中點p大于點q，則將1放入R(p)容器中，如果在第一維點p小于點q，則將0放入R(p)容器中，否則將0和1同時放入R(p)容器中；然后從第二維到第d維遍歷p和q中的數據，假設遍歷到第i維，如果在第i維點p大于點q，則將容器R(p)中的每個數與2左移i-1位相加，如果點p等于點q，則將R(p)容器中的數與2左移i-1位相加，并放入R(p)容器中，且R(p)容器中的原數據不變。需要注意的是如果點p和點q在某些維上的值相同，將得到多個區域，那么每個區域都需要進行處理。

算法2計算點p的區域號

input:任意d維數據p和查詢點q

output:點p的區域號R(p)

1.定義整型容器R(p)

2.if(p[0]＞q[0])

3.將1加入R(p)

4.else if(p[0]=q[0])

5.將1和0加入R(p)

6.else

7.將0加入R(p)

8.for(i=1;i＜ =d;i++)//表示遍歷第i維

9. if(p[i]＞q[i])

10.將R(p)中的數據都加上2＜＜(i+1)

11. else if(p[i]=q[i])

12.將R(p)中數據加上2＜＜(i+1)放入R(p)

13.returnR(p)

5 實驗結果

本文系統地測試了擴展的BBDS算法[16]和DSSW算法在ρ值、滑動窗口大小、滑動因子和數據維度變化時的性能。性能評估指標包括響應時間和滑動窗口中的數據量，顯然響應時間越短，滑動窗口中保留的數據量越小，在響應時間及存儲空間上的優勢越明顯。所有算法均采用標準C++實現，數據均采用合成的標準測試數據集，本文對獨立分布、正相關分布和反相關分布數據分別進行測試。實驗環境為Intel Core i5-4590 3.30 GHz CPU和8 GB內存的PC機。實驗中參數的主要變化范圍及其默認值如表1所示。

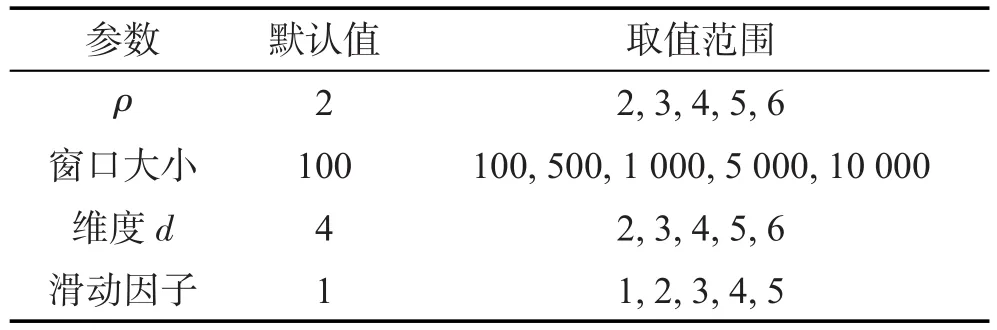
Table 1 Experimentalparameters表1 實驗參數變化范圍

首先，討論在窗口大小為100，維度為4，滑動因子為1時ρ值對算法性能的影響。圖4表示了當ρ值從2變化到6時ρ-支配輪廓集的大小變化情況，從圖中可以看出，無論是何種分布數據，隨著ρ值的增大，ρ-支配輪廓集都逐漸減小。原因在于ρ值增大導致數據所支配的面積變大，數據越容易被ρ-支配，從而使數據成為ρ-支配輪廓點的概率減小。圖5表示了ρ值對響應時間的影響，從圖中可以看出，當ρ值變化時響應時間沒有太大的改變，但是不管何種分布數據，DSSW算法由于采用了數據過濾技術、近似R樹索引和數據分類方法，響應時間都遠小于BBDS算法。圖6顯示了ρ值對滑動窗口中保留的數據量的影響，從圖中可以看出，無論是何種分布數據，滑動窗口中保留的數據量都與ρ值無關。原因在于采用的數據過濾方法是過濾掉被后到的點完全支配的點，對于相同的數據流，當ρ大于1時過濾掉的點是相同的，但是DSSW算法由于采用了數據過濾方法，滑動窗口中保留的數據量始終小于BBDS算法滑動窗口中保留的數據量。圖5和圖6的實驗結果都證明了DSSW算法的有效性。

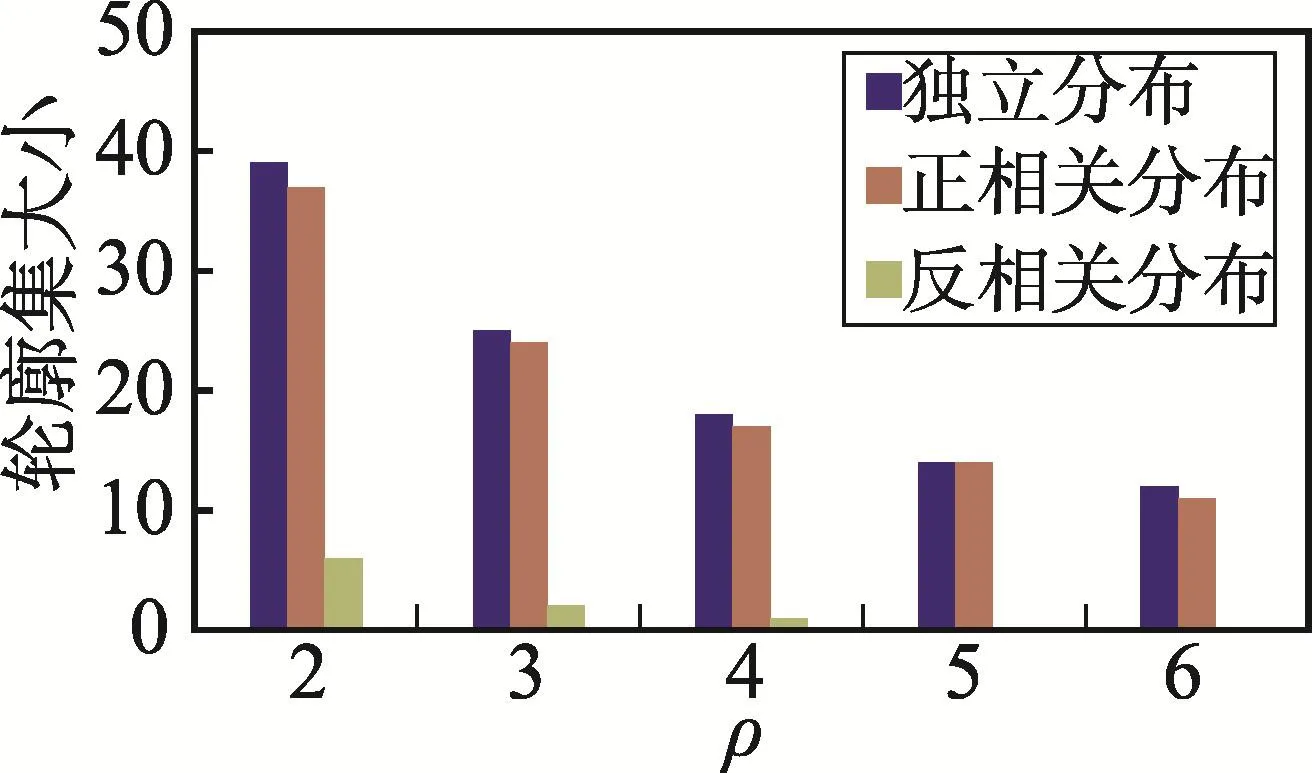
Fig.4 Effectofρon skyline size圖4 ρ值對輪廓集大小的影響

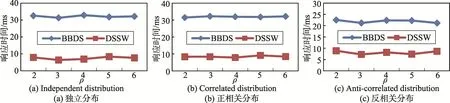
Fig.5 Effectofρon response time圖5 ρ值對響應時間的影響

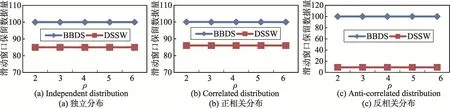
Fig.6 Effectofρon data size inw indow圖6 ρ值對窗口中保留數據量的影響

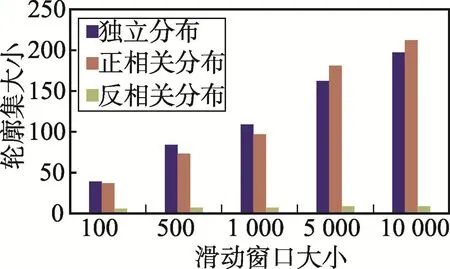
Fig.7 Effectof slidingw indow sizeon skyline size圖7 滑動窗口大小對輪廓集大小的影響

然后，討論ρ值為2，維度為4，滑動因子為1時滑動窗口的大小對算法性能的影響。圖7顯示了當滑動窗口大小變化時ρ-支配輪廓集大小的變化情況，從圖中可以看出，無論是何種分布數據，ρ-支配輪廓集都隨著滑動窗口的增大而增大。原因在于當滑動窗口增大時，參與輪廓計算的數據點增多，從而ρ-支配輪廓集增大。圖8顯示了滑動窗口大小對算法響應時間的影響，從圖中可以看出，當滑動窗口變大時，BBDS算法的響應時間急劇增加，而DSSW算法由于采用了數據過濾、近似R樹索引和數據分類，響應時間雖然增加，但始終小于BBDS算法，且滑動窗口越大，差距越明顯。圖9顯示了滑動窗口大小對滑動窗口中保留的數據量的影響，從圖中可以看出，BBDS算法的滑動窗口中保留的數據量始終與滑動窗口的大小相同，而DSSW算法隨著滑動窗口的變大，滑動窗口中保留的數據量逐漸變多，但DSSW算法由于采用了數據過濾方法，滑動窗口中保留的數據量總是遠遠小于BBDS算法的滑動窗口中保留的數據量。圖8和圖9進一步證明了DSSW算法的有效性。

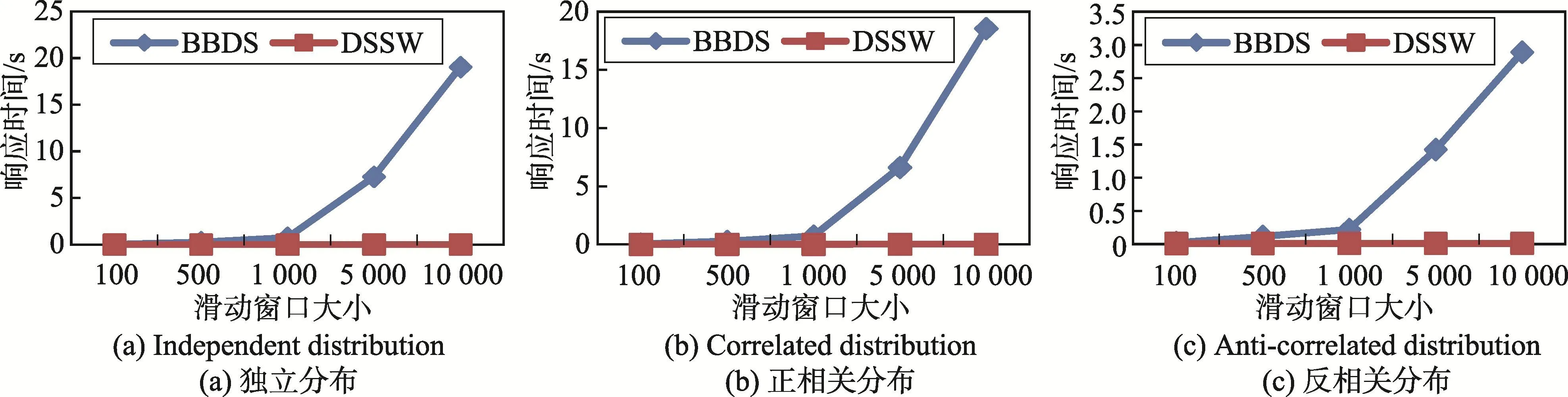
Fig.8 Effectof slidingw indow size on response time圖8 滑動窗口大小對響應時間的影響

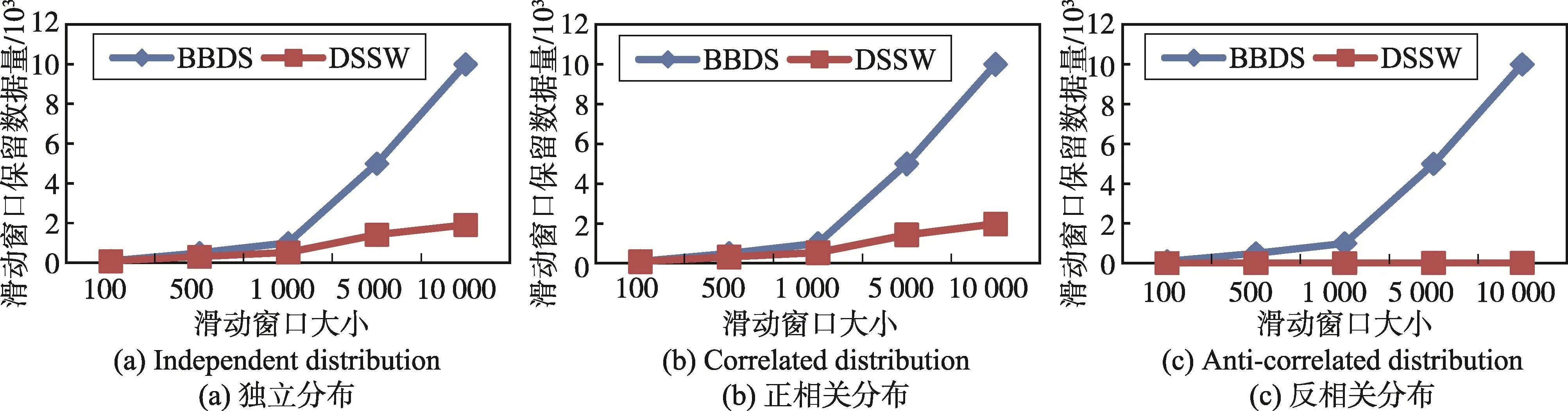
Fig.9 Effectof slidingw indow sizeon data size inw indow圖9 滑動窗口大小對窗口中保留數據量的影響

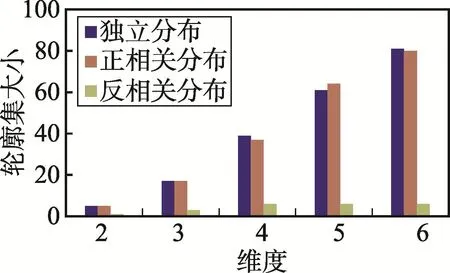
Fig.10 Effectof dimension on skyline size圖10 維度對輪廓集大小的影響

接著，討論當ρ值為2，滑動窗口大小為100，滑動因子為1時維度對算法性能的影響。圖10顯示了當維度從2變化到6時ρ-支配輪廓集的大小，從圖中可以看出，無論是何種分布數據，ρ-支配輪廓集隨著維度的增加而增大。原因在于維度增大時，數據點被ρ-支配的概率降低，數據成為ρ-支配輪廓點的可能性增大，從而ρ-支配輪廓集變大，當維度超過一定限度時，ρ-支配輪廓將為滑動窗口中的全部數據。圖11顯示了維度對響應時間的影響，從圖中可以看出，無論是何種分布數據，當維度增加時響應時間變長，但是DSSW算法的響應時間遠小于BBDS算法。圖12顯示了維度對滑動窗口中保留的數據量的影響，從圖中可以看出，BBDS算法的滑動窗口中保留的數據量始終與滑動窗口的大小相同，而DSSW算法滑動窗口中保留的數據量隨著維度的增加而逐漸增加，但數據過濾使其總是小于BBDS算法的該值。圖11和圖12進一步證明了DSSW算法的有效性。

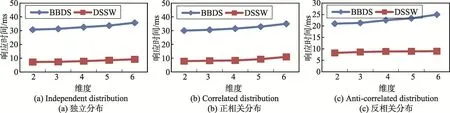
Fig.11 Effectof dimension on response time圖11 維度對響應時間的影響

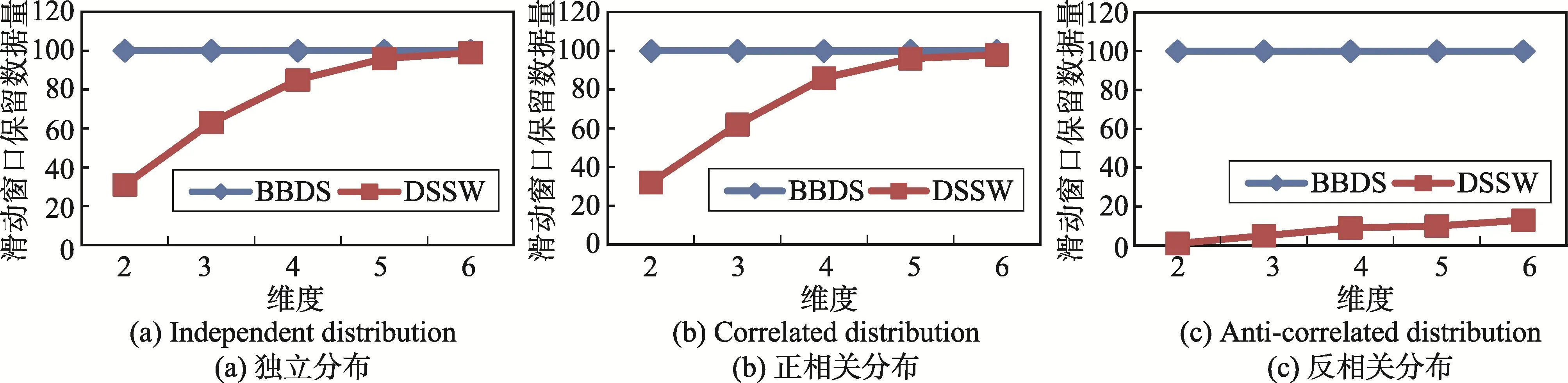
Fig.12 Effectof dimension on data size inw indow圖12 維度對窗口中保留數據量的影響

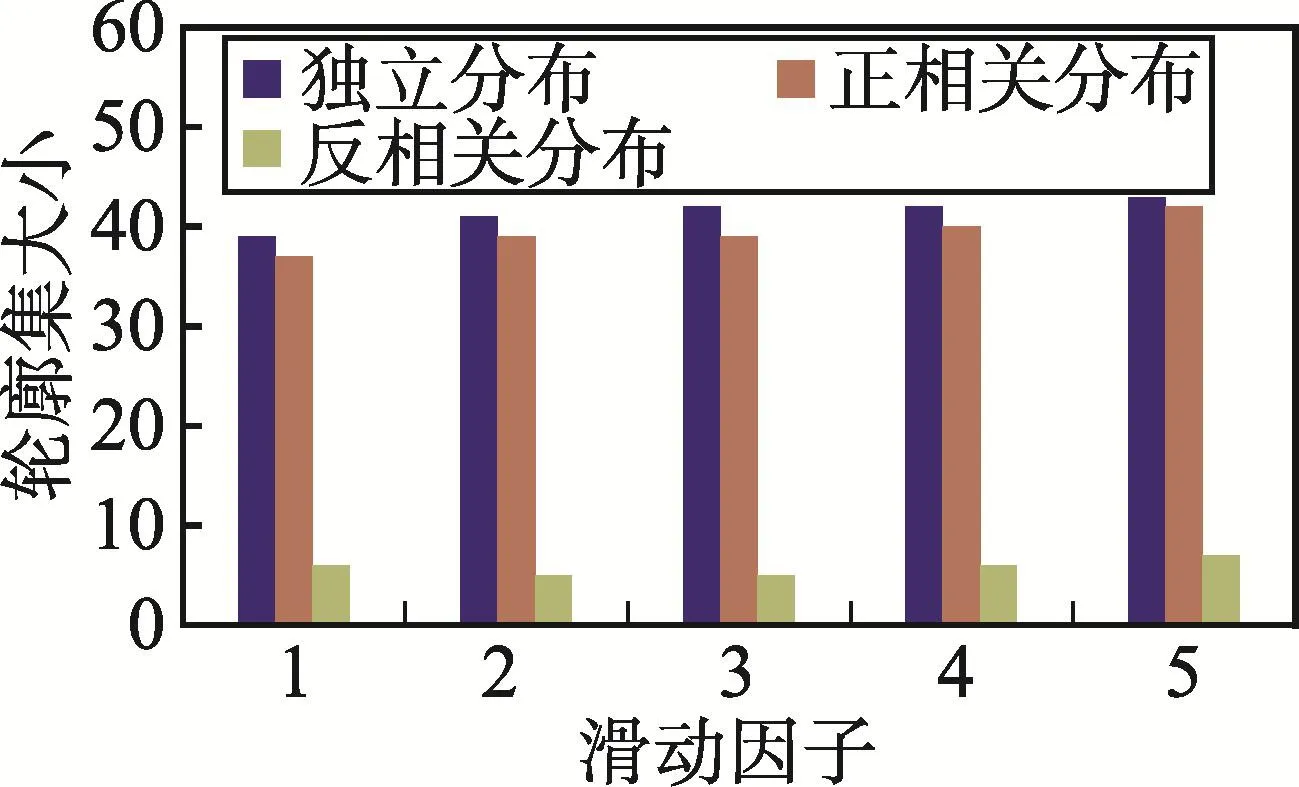
Fig.13 Effectof sliding factor on skyline size圖13 滑動因子對輪廓集大小的影響

最后，討論當ρ值為2，滑動窗口大小為100，維度為4時滑動因子對算法性能的影響。圖13顯示了當滑動因子從1變化到5時相應的ρ-支配輪廓集的大小，從圖中可以看出，無論是何種分布數據，ρ-支配輪廓集都不受滑動因子的影響。原因在于滑動因子只代表數據流更新的快慢，對數據是否成為ρ-支配輪廓點沒有影響。圖14顯示了滑動因子對響應時間的影響，從圖中可以看出，無論是何種分布數據，當滑動因子增加時響應時間變長。原因在于滑動窗口中需要更新的數據變多，需要參與ρ-支配計算的數據變多，但是DSSW算法的響應時間始終小于BBDS算法的響應時間。圖15顯示了滑動因子對滑動窗口中保留的數據量的影響，從圖中可以看出，滑動因子對滑動窗口中的數據量幾乎沒有影響，BBDS算法的滑動窗口中保留的數據量始終與滑動窗口的大小相同，而DSSW算法由于采用了數據過濾方法，滑動窗口中保留的數據量始終小于BBDS算法的滑動窗口中保留的數據量。圖14和圖15更進一步證明了DSSW算法的有效性。

6 結論

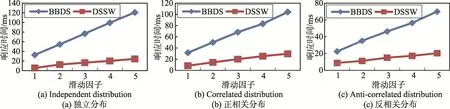
Fig.14 Effectof sliding factoron response time圖14 滑動因子對響應時間的影響

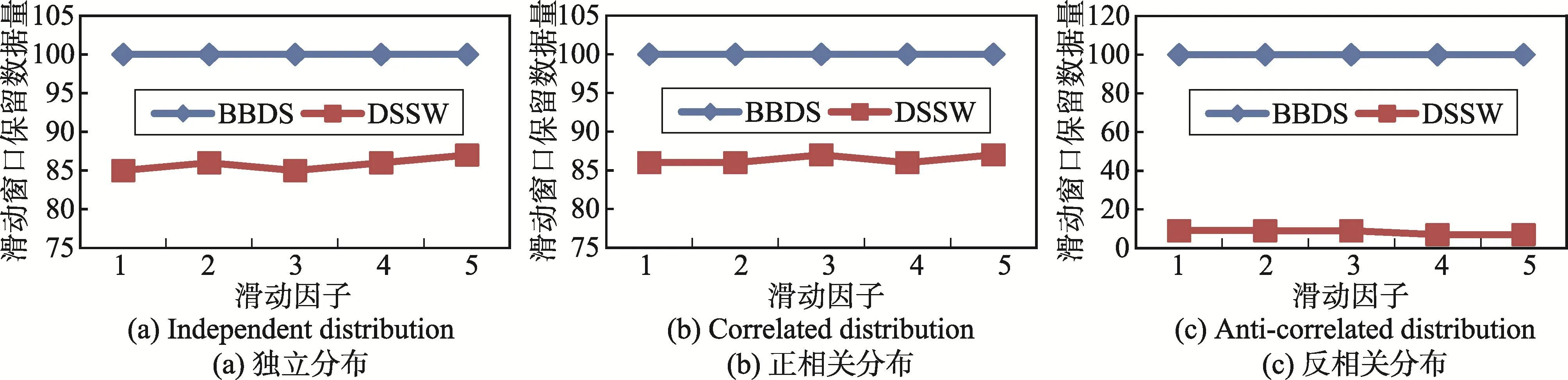
Fig.15 Effectof sliding factor on data size in w indow圖15 滑動因子對窗口中保留數據量的影響

ρ-支配輪廓查詢被廣泛應用于數值間比例關系的多標準決策中，但在數據的流特性日益突出的今天，傳統的ρ-支配輪廓查詢無法在數據更新頻繁時滿足查詢處理的實時性需求，因此本文研究了數據流上的ρ-支配輪廓查詢處理技術。首先，通過實際問題對數據流上的ρ-支配輪廓查詢的需求進行分析，給出了數據流上的ρ-支配輪廓的概念；然后，通過充分挖掘數據流上的ρ-支配輪廓的性質，建立了基于時序支配的數據過濾方法，并將數據集進行分類；接著，提出了數據流上的基于滑動窗口的ρ-支配輪廓查詢處理算法DSSW；最后，通過大量的實驗證明了DSSW算法是計算數據流上的ρ-支配輪廓的高效算法。本文基于計數的滑動窗口進行討論，從中可以看出DSSW算法能夠容易地擴展到基于時間的滑動窗口上。

[1]B?rzs?nyi S,Kossmann D,Stocker K.The skyline operator[C]//Proceedings of the 17th International Conference on Data Engineering,Heidelberg,Germany,Apr 2-6,2001.Washington:IEEEComputer Society,2001:421-430.

[2]Papadias D,Tao Yufei,Fu G,etal.An optimal and progressive algorithm for skyline queries[C]//Proceedings of the 2003 ACM SIGMOD International Conference on Managementof Data,San Diego,USA,Jun 9-12,2003.New York:ACM,2003:467-478.

[3]Chen Lei,Lian Xiang.Dynamic skyline queries inmetric spaces[C]//Proceedings of the 11th International Conferenceon Extending Database Technology:Advances in Database Technology,Nantes,France,Mar 25-29,2008.New York:ACM,2008:333-343.

[4]Chan CY,Jagadish H V,Tan K L,etal.On high dimensional skylines[C]//LNCS 3896:Proceedings of the 10th International Conference on Extending Database Technology,Munich,Germany,Mar 26-31,2006.Berlin,Heidelberg:Springer,2006:478-495.

[5]Yiu M L,Mamoulis N.Efficient processing of top-kdominating queries on multi-dimensional data[C]//Proceedings of the 33rd International Conference on Very Large Data Bases,Vienna,Austria,Sep 23-27,2007.New York:ACM,2007:483-494.

[6]Chen Lijiang,Cui Bin,Lu Hua.Constrained skyline query processing against distributed data sites[J].IEEE Transactionson Know ledge and Data Engineering,2011,23(2):204-217.

[7]Kossmann D,Ramsak F,Rost S.Shooting stars in the sky:an online algorithm for skyline queries[C]//Proceedings of the 28th International Conference on Very Large Data Bases,Hong Kong,China,Aug 20-23,2002.New York:ACM,2002:275-286.

[8]Lin Xuemin,Yuan Yidong,Wang Wei,et al.Stabbing the sky:efficientskyline computation over sliding w indows[C]//Proceedings of the 21st International Conference on Data Engineering,Tokyo,Japan,Apr 5-8,2005.Piscataway,USA:IEEE,2005:502-513.

[9]ZhangWenjie,Lin Xuemin,Zhang Ying,etal.Probabilistic skyline operator over sliding w indow s[C]//Proceedings of the 25th International Conference on Data Engineering,Shanghai,Mar 29-Apr 2,2009.Washington:IEEEComputer Society,2009:1060-1071.

[10]Ding Xiaofeng,Lian Xiang,Chen Lei,et al.Continuous monitoring of skylinesoveruncertain data streams[J].Information Sciences,2012,184(1):196-214.

[11]Yang Jing,Qu Bo,LiCuiping,etal.DC-Tree:an algorithm for skyline query on data streams[C]//LNCS 5139:Proceedings of the 4th International Conference on Advanced DataM ining and Applications,Chengdu,China,Oct8-10,2008.Berlin,Heidelberg:Springer,2008:644-651.

[12]Zhu Ling,LiCuiping,Chen Hong.Efficient computation of reverse skyline on data stream[C]//Proceedings of the 2009 International Joint Conference on Computational Sciences and Optim ization,Sanya,China,Apr24-26,2009.Washington:IEEEComputer Society,2009:735-739.

[13]Bai Mei,Xin Junchang,Wang Guoren,et al.Probabilistic reverse skyline query processing on uncertain data streams[J].Journal of Computer Research and Development,2011,48(10):1842-1849.

[14]Dellis E,V lachou A,V ladim irskiy I,etal.Constrained subspace skyline computation[C]//Proceedingsof the 15th International Conference on Information and Know ledge Management,Arlington,USA,Nov 6-11,2006.New York:ACM,2006:415-424.

[15]Morse M,Patel J,Grosky W.Efficient continuous skyline computation[J].Information Sciences,2007,177(17):3411-3437.

[16]Xin Junchang,Bai Mei,Dong Han,et al.An efficient processing algorithm forρ-dominant skyline query[J].Chinese Journalof Computers,2011,34(10):1876-1884.

附中文參考文獻：

[13]白梅,信俊昌,王國仁,等.不確定數據流上的概率反輪廓查詢處理[J].計算機研究與發展,2011,48(10):1842-1849.

[16]信俊昌,白梅,東韓,等.一種 ρ-支配輪廓查詢的高效處理算法[J].計算機學報,2011,34(10):1876-1884.

王之瓊（1980—），女，黑龍江哈爾濱人，2014年于東北大學計算機軟件與理論專業獲得博士學位，現為東北大學副教授、碩士生導師，主要研究領域為數據處理，計算機圖像處理，大數據分析等。發表學術論文40余篇，作為負責人承擔了國家自然科學基金、遼寧省自然科學基金和中國博士后科學基金等課題5項。

BA Jianm in was born in 1990.He is an M.S.candidate atNortheastern University.His research interest is Skyline query.

霸建民（1990—），男，河北景縣人，東北大學計算機科學與工程學院碩士研究生，主要研究領域為Skyline查詢處理。

HUANG Da was born in 1983.He is an M.S.candidate at School of Computer Science and Engineering,Northeastern University.His research interests include data stream,computernetwork andmachine learning,etc.

黃達（1983—），男，湖南瀏陽人，東北大學計算機科學與工程學院碩士研究生，主要研究領域為數據流，計算機網絡，機器學習等。

XIN Junchang was born in 1977.He received theM.S.and Ph.D.degrees in computer science and technology from Northeastern University in 2005 and 2008 respectively.Now he is an associate professor at School of Computer Science and Engineering,Northeastern University,and themember of CCF.His research interests include big data management,sensory datamanagement,uncertain datamanagement,cloud computing andmachine learning,etc.

信俊昌（1977—），男，遼寧遼陽人，2005年和2008年于東北大學分別獲得碩士和博士學位，現為東北大學計算機科學與工程學院副教授，CCF會員，主要研究領域為大數據管理，感知數據管理，不確定數據管理，云計算，機器學習等。

ρ-Dom inant Skyline Com putation on Data Stream s*

WANG Zhiqiong1,BA Jianm in2,HUANG Da2,XIN Junchang2+
1.Schoolof Sino-Dutch Biomedicaland Information Engineering,Northeastern University,Shenyang 110819,China
2.Schoolof Computer Scienceand Engineering,Northeastern University,Shenyang 110819,China

Skyline query on data stream can'tdirectly compute ρ-dominantskyline query,and traditionalρ-dominant skyline query can'tmeet the real-time need when data are updated frequently.So this paper proposesρ-dom inant skyline query algorithm on data stream.Firstly,the definitions of full-dom inance,ρ-dom inance and ρ-dominant skyline are introduced,and the definition ofρ-dom inant skyline on data stream is proposed.Next,a data filtering method based on time sequence dom inance is proposed by thoroughly analyzing properties aboutρ-dominantskyline on data stream,and an algorithm,calledρ-dom inantskyline query over slidingw indow(DSSW),is developed to increase the efficiency of skyline computing on data stream.Finally,extensive experiments show that the DSSW algorithm has obvious advantages in response time and storage space compared w ith traditionalρ-dominant skylinealgorithm.

iong was born in 1980.She

the Ph.D.degree in computer software and theory from Northeastern University in 2014.Now she is an associate professor and M.S.supervisor at Northeastern University.Her research interests include data processing,computer image processing and big data analytics,etc.

：TP311.13

*The NationalNatural Science Foundation of China underGrantNos.61402089,61472069,61502215(國家自然科學基金);the Fundamental Research Funds for the Central Universities of China under GrantNos.N161904001,N161602003(中央高校基本科研業務費專項資金);the Natural Science Foundation of Liaoning Province under Grant No.2015020553(遼寧省自然科學基金);the Postdoctoral Science Foundation of ChinaunderGrantNo.2016M 591447(中國博士后科學基金);the Postdoctoral Science Foundation of Northeastern University underGrantNo.20160203(東北大學博士后科研基金).

Received 2016-07,Accepted 2016-09.

CNKI網絡優先出版:2016-09-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160908.1047.028.htm l

Keywords:ρ-dom inant relationship;ρ-dom inantskyline;data stream;slidingw indow