圓筒試驗JWL狀態方程參數的貝葉斯標定＊

陳 華，周海兵，劉國昭，孫占峰，張樹道

（1．北京應用物理與計算數學研究所，北京100094；2．中國工程物理研究院流體物理研究所沖擊波物理與爆轟物理實驗室，四川綿陽621999）

圓筒試驗JWL狀態方程參數的貝葉斯標定＊

陳 華1，周海兵1，劉國昭1，孫占峰2，張樹道1

（1．北京應用物理與計算數學研究所，北京100094；2．中國工程物理研究院流體物理研究所沖擊波物理與爆轟物理實驗室，四川綿陽621999）

在研究數值模擬的輸入參數引入的不確定性時，通常需要人為給定每個輸入參數的概率分布，且輸入參數概率分布的選擇可能會對分析結果產生直接影響。利用貝葉斯方法標定了圓筒試驗JWL狀態方程參數，得到了標定參數的估計值和后驗分布，并研究了不同統計模型假設對標定參數的估計值和后驗分布的影響。貝葉斯后驗分布融合了基準試驗的試驗數據的信息，因此將其作為不確定度量化分析時輸入參數的初始概率分布，可以盡量減少分布選擇引入的認知不確定性。

不確定度量化；參數標定；后驗概率分布；貝葉斯方法；JWL狀態方程；圓筒試驗；高斯過程

隨著計算機技術的發展，數值模擬已經成為復雜系統研究及設計的重要手段。以往，研究人員常常將材料參數、幾何尺寸等作為確定性的輸入參數，代入程序進行數值模擬，從而得到確定性的結果。然而實際上，數值模擬過程中存在各種不確定性來源。近十幾年，不確定度量化（uncertainty quantification，UQ）方法發展迅速，逐漸成為數值模擬研究的熱點［12］。不確定度量化主要關注如何表征、量化、減小數值模擬過程中的各種不確定性來源，是實現高置信度數值模擬的有效手段。在進行不確定度量化分析時，為了研究輸入參數引入的不確定性，每個輸入參數常常需要人為給定概率分布。輸入參數概率分布的選擇很可能會對分析結果有直接影響，為了減少分布選擇的主觀性，輸入參數的概率分布最好能夠由試驗數據提供。

目前，圓筒試驗是評估炸藥的做功能力、確定爆轟產物狀態方程參數的基準試驗，已經得到了廣泛應用［38］。標準的圓筒試驗方法主要采用電離探針測量炸藥爆速，用高速掃描相機記錄定常滑移爆轟驅動下圓筒壁的徑向膨脹距離隨時間的變化關系，并利用經驗公式計算圓筒壁的膨脹速度和比動能等表征炸藥做功能力的特征量，最后利用這些試驗結果標定JWL（Jones－Wilkins－Lee）狀態方程的參數［910］。本文中，利用貝葉斯方法對圓筒試驗JWL狀態方程參數進行標定，給出標定參數的估計值，得到標定參數的后驗分布，然后將該后驗分布作為不確定度量化分析時輸入參數的初始分布，以減小輸入參數分布選擇引入的不確定性。

1 圓筒試驗

圓筒試驗的試驗裝置示意圖如圖1所示，高速相機VISAR從狹縫掃描記錄的是圓筒壁外表面的徑向膨脹過程，通過對照片底片的處理獲得圓筒壁的徑向膨脹位移和時間的關系。得到的觀測數據如圖2所示。炸藥爆轟產物JWL狀態方程形式和等熵條件如下：式中：p為壓力，下標“S”表示熵，V為相對比容，e為初始體積能量，A、B、C、R1、R2和ω為待標定參數。利用JWL狀態方程在C－J點的特性，由圓筒試驗和相關試驗的觀測數據得到爆壓、爆速、密度、內能和參數ω，再構造代數方程組，給定R1和R2，聯立求解A、B和C［11］。

圖1 圓筒試驗的試驗裝置示意圖Fig．1 Device of cylinder test

圖2 圓筒試驗徑向半徑和時間的關系Fig．2 Radius vs．time in cylinder test

2 貝葉斯標定方法

M．Kennedy和A．OHagan［12］提出用貝葉斯方法進行參數標定和預測。由此發展出來一系列方法，統稱為KOH方法［1315］。KOH方法用高斯過程（Gaussian process，GP）對計算結果和觀測結果進行建模，同時對模型偏差進行建模。KOH方法的主要思想是用高斯過程建立代理模型，然后用代理模型計算后驗分布和標定參數。下面簡單介紹KOH方法的框架，更多技術細節參見文獻［12］。

2．1 定義和統計模型

令X＝（X（1），…，X（qX））為qX維控制變量，θ＝（θ（1），…，θ（qθ））為qθ維標定參數，Y為數值模擬計算的輸出結果，Z為試驗觀測結果。KOH模型如下：

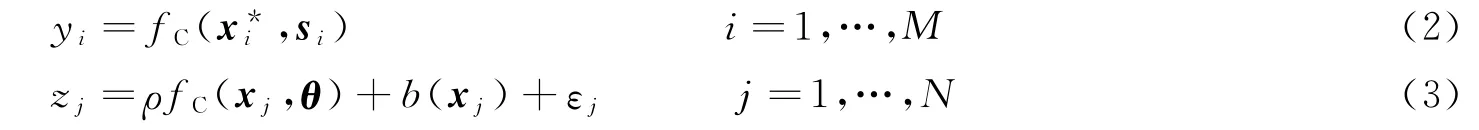
式中：fC（·）為計算模型，b（·）為模型偏差，εj為觀測誤差，ρ為回歸系數，M 為數值模擬樣本量，N為試驗樣本量，x＊i為控制變量在第i次數值模擬中的取值，xj為控制變量在第j次實驗中的取值（按照數理統計中約定，采用大寫字母表示隨機變量，相應的小寫字母表示該隨機變量的取值，本文中，“X”、“Y”、“Z”、“T”、“R1”、“R2”均采用該約定）。為了得到數值模擬的結果，需要給標定參數賦值，令s表示數值模擬時輸入的標定參數，θ表示標定參數的真實值，以便于區分。

假設εj服從均值為零、方差為λ的正態分布；fC（·）用高斯過程建模，均值函數為m1（x，s），協方差函數為c1（·，·）；模型偏差b（x）也用高斯過程建模，均值函數為m2（x），協方差函數為c2（·，·）。假設均值函數和協方差函數的形式如下：

式中：hi（·）為統計建模時任意給定的連接函數，σ2i、ωXi、ωθi為協方差函數建模中需要估計的未知參數。令ψ＝（ψ1，ψ2），ψi是協方差函數ci（·，·）中的超參數（σ2i，ωXi，ωθi），i＝1，2。KOH模型的超參數包括β＝（β1，β2）和φ＝（ρ，λ，ψ），則全部要估計的參數為（θ，β，φ）。

2．2 數據結構

數據包括觀測數據z和數值模擬結果y，即dT＝（zT，yT）。數值模擬過程中輸入變量的取值記為D1＝｛（x＊1，s1），…，（x＊M，sM）｝，試驗數據控制變量的取值記為D2＝｛x1，…，xN｝，與D1相對應，可以將D2擴充為D2（θ）＝｛（x1，θ），…，（xN，θ）｝。

2．3 后驗分布

令先驗分布P（β）∝1。根據貝葉斯理論，在給定先驗分布的條件下，后驗分布為：

式中：f（d；md（θ），Vd（θ））是多元正態分布N（md（θ），Vd（θ））的密度函數，且

式中：H1、H2為由連接函數hi構成的向量，V1（D1）為由集合D1中數據構成的方差矩陣，V2（D2）為由集合D2中數據構成的方差矩陣，C1為D1和D2中數據構成的協方差矩陣，IN為N維單位矩陣。

2．4 計算步驟

直接計算式（6）中的后驗分布較困難，因此將計算過程分為4個步驟：步驟1和步驟2是建立GP模型，步驟3是用建立的GP模型計算后驗分布，步驟4是利用步驟3得到的后驗分布標定參數。

步驟1：建立GP代理模型，估計β1和c1（·，·）的超參數ψ1。用數值模擬所得數據y估計β1和ψ1，得到估計值步驟2：建立觀測數據的GP代理模型，估計ρ、λ、β2和c2（·，·）的超參數ψ2。在給定的條件下，用觀測數據z估計ρ、λ、β2和c2（·）的超參數ψ2，從而得到估計值步驟3：計算標定參數θ的后驗分布。由于，因此通過計算即可得到θ的后驗分布。步驟4：利用θ的后驗分布標定參數。標定參數的估計可以定義為后驗分布的均值＾θ（mean）、中位數＾θ（mid）或最大概率值＾θ（max），其中＾θ（max）也稱為最大后驗估計（maximum posterior estimates，MPE）。

3 JWL狀態方程參數的標定

采用KOH貝葉斯方法標定圓筒試驗JWL狀態方程參數。將標定參數記為（R1，R2）；將時間視為設計變量，記為T；同時令M＝30，N＝10。數值計算過程中，R1和R2的抽樣區間分別為［4．3，5．5］和［0．8，1．5］，用拉丁超立方抽樣（latin hypercube sample，LHS）方法得到M組參數并代入模擬程序進行計算，得到M條徑向半徑隨時間變化的曲線。對設計變量T進行LHS抽樣得到M個樣本。將T和（R1，R2）的樣本隨機配對得到模擬計算的輸入數據D1＝｛（t＊1，R11，R21），…，（t＊M，R1M，R2M）｝。D1對應的計算輸出結果為y＝｛y1，…，yM｝。需要注意的是，每次數值計算的結果都是徑向半徑隨時間變化的曲線，這里只是從曲線上隨機取一個抽樣點作為輸出結果。對時間變量T隨機抽樣得到N 個樣本，即D2＝｛t1，…，tN｝。將D2擴充為D2（r1，r2）＝｛（t1，r1，r2），…，（tN，r1，r2）｝，其中（r1，r2）是標定參數的真實值。D2（r1，r2）對應的徑向半徑觀測數據為z＝｛z1，…，zN｝。假設（R1，R2）的先驗分布為均勻分布，即對（R1，R2）沒有任何知識；超參數ψ的先驗分布為標準正態分布。數值模擬使用的計算程序為由北京應用物理與計算數學研究所自主研制的相容拉氏流體動力學工具包CHAP（compatible hydrodynamics analysis program）［16］。

下面分別采用兩個模型進行建模，其主要區別在于模型中是否包含偏差。模型1是KOH模型的通用形式，如式（2）～（3）所示；模型2是KOH模型的特殊形式，相當于在模型1的基礎上令ρ＝1，b（xj）≡0，此時式（3）可以簡化為：

按照第2．4節中的4個步驟依次進行計算。第1步是建立數值模擬的GP代理模型。GP代理模型中參數的估計值分別為為檢驗GP代理模型預測的能力，重新隨機抽樣4組（R1，R2）樣本代入數值模擬程序進行計算，將計算得到的結果和采用GP模型預測的結果進行比較，如圖3所示。從圖3可以看出：代理模型預測曲線和數值計算的曲線基本重合，說明代理模型的預測足夠精確。第2步是建立觀測數據的GP代理模型。模型1中模型參數的估計值分別為由于模型2忽略了模型偏差并且ρ＝1，所以該步驟中只需要估計λ，估計值為第3步是計算標定參數的后驗分布。圖4給出了標定參數（R1，R2）的后驗概率分布等高線，其中后驗概率共分為9個概率區間，分別由9種顏色進行區分，從小到大依次用Pk（k＝1，…，9）表示，P9表示最大概率區間的值域。圖4（a）為采用模型1得到的后驗概率分布，可以看出，概率分布從右下角向左上角逐級遞增，概率最大區域P9位于左上角；圖4（b）為采用模型2得到的后驗概率分布，可以看出，概率分布從右下角和左邊向中間區域逐級遞增，P9近似位于中間位置。第4步是標定參數。由圖4可知：模型1的MPE為兩個模型的MPE均近似位于P9區域的中心位置。

圖3 GP代理模型預測的結果和數值計算結果的比較Fig．3 Comparison of predictions of the GP surrogate model with numerical simulations

圖4 兩模型的后驗概率等高線和最大后驗估計Fig．4 Posterior distribution and MPE with different models

圖5為模型1和模型2的預測效果，其中標定結果（紅線）是將MPE代入數值模擬程序計算得到，預測結果（綠線）采用觀測數據的GP代理模型計算得到，試驗結果用黑線表示。圖5顯示：兩個模型的預測結果均與試驗結果符合很好，說明建立的代理模型都能夠比較精確地描述試驗數據。模型2中試驗結果和標定結果符合得比較好，表明標定的參數值是最佳擬合的估計；但是，當t＞39μs時，模型1的標定結果和試驗結果差異逐漸增大。由于數值模擬和基于觀測數據代理模型的預測（即和）都足夠精確，所以兩者的差異即為模型偏差的預測＾b（x），說明模型1標定的參數值是“調和”了模型偏差和標定參數的最佳估計。

圖5 徑向半徑的預測、試驗和模擬結果的比較Fig．5 Comparison of radius histories obtained by prediction，experiment and simulation

4 結 論

（1）用KOH貝葉斯方法標定圓筒試驗JWL狀態方程的參數R1和R2，得到了標定參數的估計值和后驗分布，并將后驗分布作為子系統級（或系統級）復雜系統數值模擬不確定度量化分析的輸入參數的初始分布，以盡可能地減少分布選擇引入的認知不確定性。（2）分析了兩種KOH統計模型假設對標定參數估計值和后驗分布的影響。從參數標定的角度分析，模型2得到的估計值更好；從不確定度量化的角度分析，由于模型1還分析了模型偏差引入的不確定性，因此模型1更合適。

［1］ Oberkampf W L，Roy C J．Verification and validation in scientific computing［M］．Cambridge：Cambridge University Press，2010．

［2］ Smith R C．Uncertainty quantification：Theory，implementation，and applications［M］．Philadelphia：Society for Industrial and Applied Mathematics，2013．

［3］ Kury J W，Honig H C，Lee E L，et al．Metal acceleration by chemical explosives［C］∥4th Symposium on Detonation．Maryland：White Oak，1966：3－13．

［4］ Lan I F，Hung S C，Chen C Y，et al．An improved simple method of deducing JWL parameters from cylinder expansion test［J］．Propellants，Explosives，Pyrotechnics，1993，18（1）：18－24．

［5］ 于川，劉文翰，李良忠，等．鈍感炸藥圓筒試驗與爆轟產物JWL狀態方程研究［J］．高壓物理學報，1997，11（3）：227－233．Yu Chuan，Liu Wenhan，Li Liangzhong，et al．Studies on cylinder test and JWL equation of state of detonation product for insensitive high explosive［J］．Chinese Journal of High Pressure Physics，1997，11（3）：227－233．．

［6］ 陳朗，黃毅民，馮長根．含鋁炸藥圓筒試驗及爆轟產物JWL狀態方程研究［J］．火炸藥學報，2001，24（3）：13－15．Chen Lang，Huang Yimin，Feng Changgen．The cylinder test and JWL equation of state detontion product of aluminized explosives［J］．Chinese Journal of Explosives and Propellants，2001，24（3）：13－15．

［7］ 陳朗，李澤仁．激光速度干涉儀測量法在炸藥圓筒試驗中的應用［J］．爆炸與沖擊，2001，21（3）：229－232．Chen Lang，Li Zeren．The cylinder tests measured by VISAR interferometer［J］．Explosion and Shock Waves，2001，21（3）：229－232．

［8］ 徐輝，孫占峰，李慶忠．標準圓筒試驗數據處理和不確定度評定方法［J］．北京理工大學學報，2010，30（5）：626－630．Xu Hui，Sun Zhanfeng，Li Qingzhong．Study on data processing and uncertainty evaluation of standard cylinder test［J］．Transactions of Beijing Institute of Technology，2010，30（5）：626－630．

［9］ Lee E L，Tarver C M．Phenomenological model of shock initiation in heterogeneous explosives［J］．Physics of Fluids，1980，23（12）：2362－2372．

［10］ Wescott B L，Stewart D S，Davis W C．Equation of state and reaction rate for condensed－phase explosives［J］．Journal of Applied Physics，2005，98（5）：053514．

［11］ 孫承緯，衛玉章，周之奎．應用爆轟物理［M］．北京：國防工業出版社，2000．

［12］ Kennedy M，OHagan A．Bayesian calibration of computer models（with discussion）［J］．Journal of the Royal Statistical Society Series B：Statistical Methodology，2001，68：425－464．

［13］ Williams B，Higdon D，Gattiker J，et al．Combining experimental data and computer simulations，with an application to flyer plate experiments［J］．Bayesian Analysis，2006，1（1）：765－792．

［14］ Higdon D，Gattiker J，Williams B，et al．Computer model calibration using high－dimensional output［J］．Journal of the American Statistical Association，2008，103（482）：570－583．

［15］ Bayarri M J，Berger J O，Rui P，et al．A framework for validation of computer models［J］．Technometrics，2007，49（2）：138－154．

［16］ 張樹道，周海兵，熊俊．相容拉氏流體動力學CHAP程序研制及其應用研究：GF－A0091846G［R］．2005．

Bayesian calibration for parameters of JWL equation of state in cylinder test

Chen Hua1，Zhou Haibing1，Liu Guozhao1，Sun Zhanfeng2，Zhang Shudao1

（1．Institute of Applied Physics and Computational Mathematics，Beijing100094，China；2．Laboratory for Shock Wave and Detonation Physics Research，Institute of Fluid Physics，Chinese Academy of Engineering Physics，Mianyang621999，Sichuan，China）

Since probability distributions of input parameters are usually assigned subjectively for uncertainty quantification（UQ）in numerical simulations，the selection of distributions may have significant effect on analysis results of UQ．In this paper，to calibrate more precisely the parameters of JWL equation of state in the cylinder test，we proposed to adopt Bayesian methods that provide estimators and posterior distributions of calibration parameters．Further，we investigated the effects of model assumptions on estimators and posterior distributions of calibration parameters．Our study shows that，owing to the information of cylinder tests they contain，the posterior distributions can be used as initial probability distributions of the input parameters in UQ to reduce the epistemic uncertainty．

uncertainty quantification；calibration；posterior distribution；Bayesian methods；JWL equation of state；cylinder test；Gaussian process

O381國標學科代碼：13035

A

10．11883／1001－1455（2017）04－0585－06

（責任編輯 王玉鋒）

2015－12－30；

2016－04－25

國家自然科學基金項目（11472060，11671413）；中國工程物理研究院科學技術發展基金項目（2013A0101004，2015B0201037）；北京應用物理與計算數學研究所所長青年基金項目（ZYSZ1518－13）

陳 華（1979－ ），女，博士，副研究員，chen＿hua＠iapcm．ac．cn。