基于局部相互作用理論的侵徹彈頭部形狀優化及仿真＊

鄧佳杰，張先鋒，2，葛賢坤，3，陳東東，郭 磊

（1．南京理工大學智能彈藥技術國防重點學科實驗室，江蘇南京210094；2．解放軍理工大學爆炸沖擊防災減災國家重點實驗室，江蘇南京210007；3．中國人民解放軍95856部隊，江蘇南京210000）

基于局部相互作用理論的侵徹彈頭部形狀優化及仿真＊

鄧佳杰1，張先鋒1，2，葛賢坤1，3，陳東東1，郭 磊1

（1．南京理工大學智能彈藥技術國防重點學科實驗室，江蘇南京210094；2．解放軍理工大學爆炸沖擊防災減災國家重點實驗室，江蘇南京210007；3．中國人民解放軍95856部隊，江蘇南京210000）

以局部相互作用理論為基礎，引入與彈體頭部形狀相關的開坑計算方法和歸一化彈體頭部形狀方程，給出了任意頭部形狀彈體侵徹混凝土深度的計算模型。利用最大侵深法，得到了無量綱頭部形狀控制參數表達式及經典變分頭部形狀優化設計方法。理論計算及彈靶分離仿真模擬計算結果與實驗結果吻合較好。研究結果表明：彈體頭部相對半徑較小時，球頭錐形和球頭卵形彈體優化后得到的頭部形狀分別為尖頭錐形和尖頭卵形；優化截頭彈體的侵徹深度大于優化尖頭彈體，而優化截錐形彈體的侵徹深度最大；彈體頭部形狀對彈體侵徹過載的影響顯著，優化彈體頭部形狀可以有效地提高侵徹深度。

侵徹彈；混凝土靶；局部相互作用模型；彈體頭部形狀優化

動能彈對混凝土目標的沖擊侵徹效應是鉆地武器研發領域的重點研究內容之一。彈體侵徹深度是表征其破壞效能的關鍵參數。彈體頭部作為侵徹過程中彈、靶的主要接觸區域，其形狀影響彈體的侵徹過程，進而影響侵徹深度和過載特性。因此，彈體頭部形狀優化具有十分重要的意義。

局部相互作用理論作為一種數學方法論，近年來引起了國外學者的重視，并開始應用于動能彈侵徹及彈體頭部形狀優化研究。A．I．Bunimovich等［1］最早提出密實介質間的局部相互作用理論。G．Ben－Dor等［29］利用最大侵徹深度和最小貫穿剩余速度優化了彈體頭部形狀和靶體結構，并開展了多種類型靶體侵徹和貫穿問題的局部相互作用模型研究。G．Yakunina［1013］研究了摩擦形式對基于局部相互作用模型計算彈體侵徹深度的影響，并通過優化得到了星形頭部和“U”形刻槽頭部彈體；F．Ragnedda等［14］采用粒子群優化算法和局部相互作用模型，得到了優化楔形頭部彈體；S．E．Jones等［15］基于不計及開坑的侵徹深度計算模型，由最小二乘法優化得到彈體頭形函數；X．W．Chen等［16］基于動態空腔膨脹模型，提出了適用于不同頭部形狀彈體侵徹半無限靶過程的分析模型；皮愛國等［17］、劉堅成等［1819］利用最小阻力法得到彈形系數，并采用變分法優化了復雜頭部形狀函數及分段卵形頭部彈體，該優化過程為后續研究提供了較好的方法論支撐。在當前的實際應用中，復雜頭部形狀彈體由于適應性不好、加工工藝復雜等缺點很難實現。針對目前的工程實際需求，動能彈侵徹混凝土靶標研究中亟待解決的是傳統侵徹彈頭部形狀的優化問題。

本文中基于局部相互作用理論和彈體頭部形狀優化的相關研究工作，結合侵徹開坑計算方法，提出任意頭部結構彈體侵徹混凝土靶的局部相互作用模型，用以預測彈體的侵徹深度；在此基礎上，開展典型的常規侵徹彈體頭部形狀優化研究，采用最大侵深法得到無量綱彈體頭部形狀控制參量表達式；利用變分優化方法，得到最佳侵徹深度對應的彈體優化頭部形狀，同時利用彈靶分離數值模擬方法，對比分析優化后彈體的侵徹深度及侵徹過程參數的變化規律。

1 彈體侵徹混凝土靶的局部相互作用理論

1．1 局部相互作用理論簡介

局部相互作用理論的基本思想［12］是彈靶間的完整作用由彈靶接觸區域所有微元的相互作用疊加而成。任意微元ds由彈體幾何形狀、彈體運動學參數及靶體材料特性決定。如圖1所示，在侵徹速度v時刻，微元ds受內法向（內法向單位矢量en）和切向（切向單位矢量eτ）兩部分作用力。

根據作用力與速度方向單位矢量ev的坐標關系，當單元Δs趨近于零時，作用于微元上的力為［2］：

式中：u＝ev·（－en）＝cosφ，Ωn（u，v）和Ωτ（u，v）分別表示局部相互作用模型的靶體正應力和切應力。

如圖2所示，建立柱坐標系（x，ρ，θ），假設彈體為剛性，彈體頭部長度為L，彈體半徑為R，截平面半徑為r，則歸一化彈體頭部形狀方程可表示為：

在速度v時刻，作用于彈體的表面阻力為：

圖1 任意頭部形狀彈體局部相互作用模型Fig．1 Local interaction model of projectile with arbitrary nose－shape

圖2 任意頭部形狀彈體結構示意Fig．2 Structure diagram of projectile with arbitrary nose－shape

根據彈靶相對位置的不同，侵徹過程中彈靶的相互作用可分為兩個階段（如圖3所示）：第1階段為彈體頭部局部區域與靶體接觸，第2階段為彈體頭部完全與靶體接觸。彈靶接觸區域Θ（h）表示為：

式中：h為彈體瞬時侵徹深度。

圖3 彈靶相互作用區域示意Fig．3 Interaction region between projectile and target

1．2 任意頭部形狀彈體侵徹混凝土深度計算模型

局部相互作用理論需借助空腔膨脹模型確定靶體阻力函數。基于修正的動態空腔膨脹模型［2021］，擬合得到靶體阻力函數三項式：

式中：Yt為混凝土無圍壓強度，ρt為混凝土密度，參數a1、a2、a3為混凝土材料的相關系數。由滑動摩擦系數μ可確定靶體切應力Ωτ（u，v）＝μΩn（u，v）。若彈體頭部存在截平面，則式（3）可改寫為：

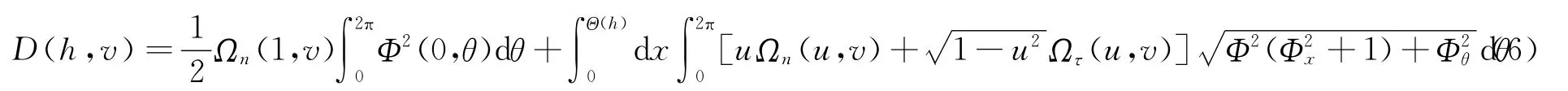
式中：Φx和Φθ分別表示Φ對x和θ的偏導數；等號右邊第1項為彈體頭部截平面作用力，第2項為側表面區域作用力。式（6）中：

將彈靶間表面應力的表達式代入式（7），侵徹速度v時刻彈體表面阻力可簡化為：

式中：Bi（i＝0，1，2）為過程參量。若考慮混凝土侵徹開坑階段，則當彈體進入穩定侵徹階段，彈體頭部完全侵入靶體，彈靶相互作用可視為彈體頭部與靶體完全接觸，由此給出式（8）對應的Bi值：

基于局部相互作用理論思想，采用混凝土侵徹兩階段模型，給出任意頭部形狀彈體侵徹混凝土深度的計算模型。開坑區的侵徹深度h1可表示為［2223］：

以開坑深度為邊界條件，侵徹過程中彈體的阻力可表示為：

式中：D＊表示開坑階段任意頭部形狀彈體的截平面區域阻力，κ為開坑階段的阻力系數。

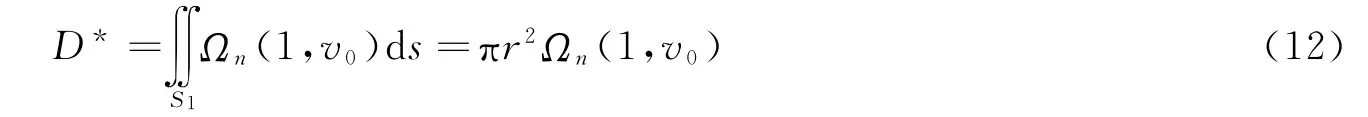
式中：S1為彈體截平面面積，v0為彈體初始侵徹速度。開坑階段與穩定侵徹階段過渡處的速度v1和開坑階段阻力系數κ由以下方程組求解：

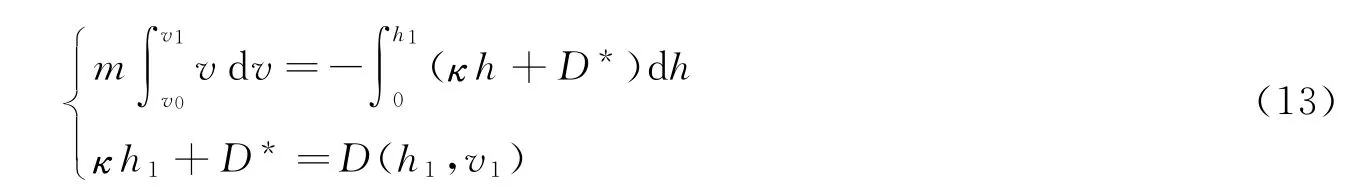
式中：m為彈體質量。由此，彈體侵徹混凝土靶的深度P可表示為：

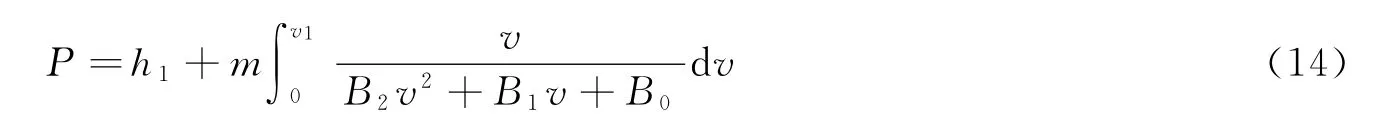
1．3 彈體侵徹混凝土靶局部相互作用模型有效性驗證

在上述理論推導的基礎上，參考國內外學者開展的不同頭部形狀彈體侵徹半無限混凝土靶實驗［2428］，驗證任意頭部形狀彈體侵徹混凝土靶的局部相互作用模型的有效性。

表1列出了尖卵形、截卵形及尖錐形彈體侵徹混凝土靶實驗的彈靶參數［2428］，其中dp為彈體直徑，σc為無圍壓強度。對比圖4所示的侵徹深度的理論計算和實驗結果，可以看出：對于不同頭部形狀彈體侵徹混凝土靶問題，理論計算結果與實驗結果吻合較好，彈體侵徹混凝土靶局部相互作用模型能較準確地預測任意頭部形狀彈體的侵徹深度。

表1 彈體模型參數及混凝土材料參數Table 1 Parameters for projectile geometry model and concrete material

圖4 不同頭部形狀彈體侵徹混凝土的局部相互作用模型計算結果與實驗數據對比Fig．4 Comparison of local interaction model calculation with experimental results for projectiles with different nose shapes penetrating into concrete

2 彈體頭部形狀數值優化

2．1 基于最大侵深法的彈體頭部形狀優化

彈體頭部形狀優化方法可分為最小阻力法和最大侵深法［28］。最小阻力法是采用侵徹阻力最小化的思想優化彈體頭部形狀［17］，而最大侵深法則是通過使彈體侵徹深度最大來優化彈體頭部形狀。利用優化方法確定的頭部形狀控制參數和最優控制理論，可得到數值優化的彈體頭部形狀。基于1．2節的侵徹深度模型，采用最大侵深法優化彈體頭部形狀。

針對靶體不可壓縮彈塑性模型的空腔膨脹理論［29］，擬合靶體阻力函數，得到包含慣性項和靶體強度項的兩項式模型，即式（5）中的黏滯阻力項為零（a1＝0）。由此，式（14）改寫為：

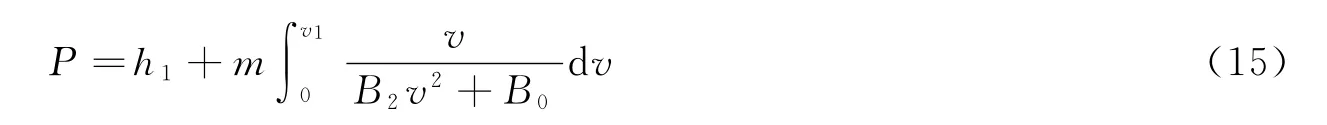
求解式（15）的積分項，并進行無量綱化處理，得到：

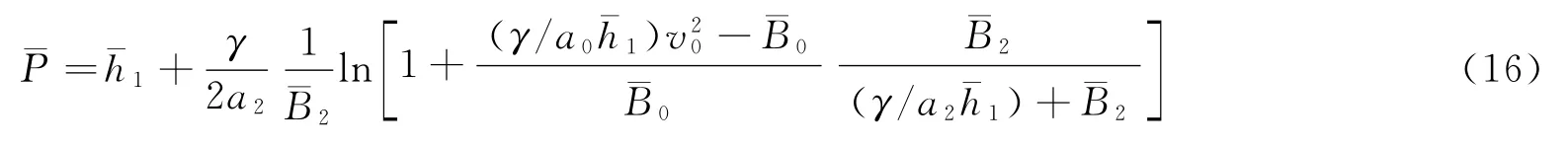
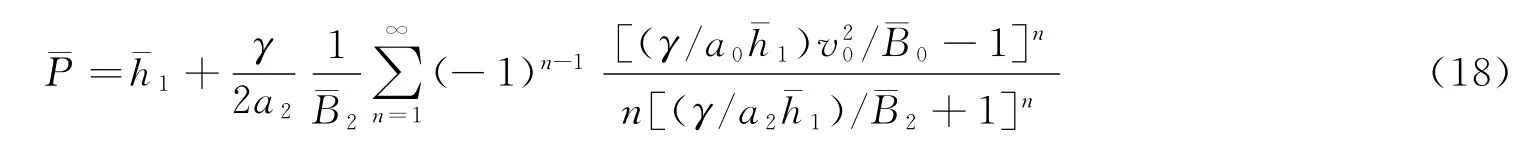
由此，頭部形狀控制參數J可表示為：

利用最大侵深法，頭部形狀控制參數J在［0，1］區間取極大值時，Φ即為最優化彈體頭部形狀。

2．2 優化算法

由2．1節可知，給定靶體材料參數、侵徹初速度、彈體質量及彈體頭部長徑比時，頭部形狀控制參數是唯一影響彈體侵徹深度的量。在最優控制理論中，頭部形狀控制參數J的目標函數為彈體頭部形狀方程，通過數值優化方法可以確定優化彈體頭部形狀方程最優解。對于目標函數的全局極值問題，可通過經典變分方法［1，17］求解，構造目標函數的泛函形式：

在彈體頭形方程一階可導及其方程邊界條件的限定下，利用泛函的歐拉－拉格朗日微分方程，可確定目標函數的全局極值。對于所需求解的最優化彈體頭形方程，應滿足以下條件：

給定彈體頭形方程中的變量關系及范圍，求解得到泛函極值處的最優化彈體頭形方程：

式中：ci為常數，表示給定形式的彈體頭形方程未知參數。

2．3 典型彈體頭部形狀的最優化彈形輪廓

基于彈體頭部形狀優化的相關研究［1219］，利用最大侵深法對傳統頭部形狀彈體進行數值優化，開展尖卵形、尖錐形、截卵形、截錐形、截球形、球頭錐形和球頭卵形彈體頭部形狀控制參數極值及相應的優化頭部形狀輪廓研究。

圖5為彈體頭部相對半徑R／L對應的彈體頭部形狀控制參數極值Jmax。其中，截卵形、尖錐形、截錐形、球頭錐形彈體的頭部形狀控制參數變化規律與G．Ben－Dor等［2］的計算結果基本一致，由此證明基于局部相互作用模型的彈體頭部形狀控制參數優化計算的正確性。由圖5所示的優化結果可知，當R／L≤0．2時，各彈形的頭部形狀控制參數極值的差異較小，各彈形的侵徹深度接近；當0．2＜R／L≤0．5時，優化截錐形彈體的頭部形狀控制參數極值最大，即優化截錐形彈體具有更大的侵徹深度，并且隨著彈頭相對半徑的增大，頭部形狀控制參數極值的增加趨勢顯著；當0．5＜R／L≤1．0時，各彈形的頭部形狀控制參數極值的差異明顯，優化頭部形狀彈體的侵徹深度由大到小依次為截錐形、球頭錐形或尖錐形、截卵形、尖卵形、截球形彈體，其中球頭錐形與尖錐形彈體的侵徹深度相同，球頭卵形彈體在0．6＜R／L＜0．9處的頭部形狀控制參數極值相對較大；當R／L＞1．0時，優化的截錐形、尖卵形、截卵形及球頭卵形彈體的頭部形狀控制參數變化保持線性增加，而其余3種優化頭部形狀彈體的頭部形狀控制參數隨R／L的增加趨于平緩。就圖5所示的彈頭相對半徑區間而言，截錐形彈體的侵徹深度最大。

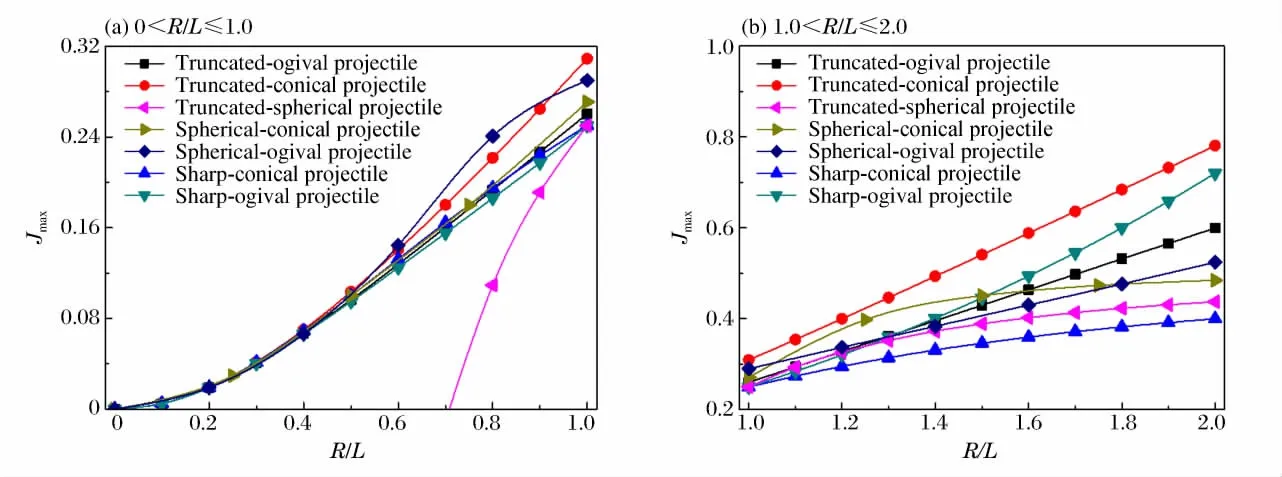
圖5 典型回轉形彈體頭部形狀控制參數最優值Fig．5 Optimized control parameters of nose－shape for typical revolution projectiles

圖6 相對球頭半徑與頭部形狀控制參數的變化關系Fig．6 Control parameter of nose－shape vs．normalized spherical radius

由R／L與相對球頭半徑（r′／L）、頭部形狀控制參數的變化關系可知：當R／L＜1．0時，球頭錐形和尖錐形彈體的頭部形狀控制參數極值相同，如圖6（a）所示，即球頭錐形彈體頭部形狀輪廓的優化結果為尖錐形彈體；當R／L≥1．0時，最優化球頭彈體的r′／L在（0．5，1．0］范圍內。球頭卵形彈體的優化結果與球頭錐形彈體的優化結果類似：當R／L≤0．5時，優化的球頭卵形彈體結構為球頭半徑為零的尖卵形彈體；當R／L＞0．5時，R／L滿足球頭卵形彈體頭形方程，即可通過優化方法計算得到如圖6（b）所示的頭部形狀控制參數極值。從圖6（b）可以看出，當R／L≥1．0時，優化截錐形彈體頭部形狀控制參數隨r′／L的增加呈現先增加后減小的趨勢，在曲線峰值處截錐形彈體取得最優解。

考慮到侵徹彈體的實際運用（即R／L較小的情況），利用式（23）的頭部形狀控制參數及變分優化方法，得到R／L＝0．5時的彈體頭部外形，如圖7所示。由于R／L＝0．5時球頭錐形和球頭卵形彈體的優化結果為相應的尖錐形和尖卵形優化彈體，因此圖7僅給出最大侵徹深度對應的尖卵形、截卵形、尖錐形、截錐形4種彈體的優化頭部形狀輪廓。

圖7 最優化彈體頭部形狀輪廓Fig．7 Optimized nose－shape of projectile

3 優化結構彈體侵徹混凝土時彈靶分離的數值模擬

3．1 有限元建模及彈靶分離方法

彈靶分離方法是將侵徹過程中的靶體阻力直接施加在彈體受力表面，以代替彈靶接觸響應。彈靶分離方法省略了靶體建模和彈靶接觸計算，極大地提高了運算速率。該方法已在侵徹分析中得到了廣泛運用，在模擬計算中的適用性較好［3032］。

本文中基于ABAQUS開展彈靶分離方法研究，建立彈體三維全模型，如圖8所示，彈體網格采用8節點六面體線性減縮積分單元進行劃分，任意單元節點的阻力用式（5）表示。給定彈體模型和邊界條件，并編寫VDLAOD子程序，在任意一個時間步，由子程序計算彈體表面正應力，并將該時刻的彈體表面正應力施加于符合條件的彈體表面單元上。在每一時間步調用所有選定單元，并將靶體響應力反饋至ABAQUS／Explicit顯式動態分析主程序，通過疊加所有單元所受的表面正應力，確定該時刻彈體的合阻力。

［24，26－27］的實驗數據，驗證彈靶分離方法的有效性。對比尖卵形、尖錐形及截卵形彈體對混凝土侵徹深度的實驗和模擬結果，如圖9所示。可以看出，模擬結果與實驗數據吻合較好，說明基于彈靶分離方法的數值模擬能夠較好地預測不同頭部形狀彈體侵徹混凝土靶的侵徹深度。

圖8 基于彈靶分離方法的彈體模型Fig．8 Projectile model based on projectile－target separation method

圖9 彈體侵徹混凝土的模擬結果與實驗數據對比Fig．9 Comparison of simulation with experiment for projectiles penetrating into concrete

3．2 優化結構彈體侵徹混凝土的數值模擬

為驗證不同優化頭部形狀彈體的侵徹能力，利用彈靶分離數值模擬方法開展優化后的尖錐形、尖卵形、截錐形和截卵形彈體侵徹C35混凝土靶數值模擬研究。

利用文獻［24］中的彈體參數（長度、直徑和質量）和靶體材料參數，構造如圖7所示的優化頭部形狀彈體模型。為保證數值計算精度和彈體網格質量，同時減少計算時間，彈體網格尺寸設置為2mm。圖10顯示了數值模擬中優化彈體的頭部結構。

圖10 優化頭部形狀彈體模型Fig．10 Numerical simulation model of optimal projectiles

圖11給出了不同頭部形狀彈體以不同初始侵徹速度侵徹混凝土時侵徹深度的計算結果。可以看出：當初始侵徹速度較低時（v0≤400m／s），不同頭部形狀彈體所得侵徹深度的差異不明顯；在中、高速段（v0＞400m／s），優化截錐形彈體具有明顯的優勢，相對于尖卵形彈體，其在1 000m／s下的侵徹深度提高達11．8%；與尖錐形和尖卵形彈體相比，優化截頭形彈體的侵徹能力更好。該結果可為傳統回轉體頭部形狀侵徹彈的優化設計提供一定的參考。

為了研究彈體頭部形狀對侵徹過程量的影響，分析了加速度a和瞬時侵徹深度h隨時間t的變化。由圖12（a）可知，開坑結束后，各彈形彈體侵徹的加速度峰值及加速度衰減趨勢的差異明顯。如圖12（b）所示，侵徹深度經過開坑區的線性增長后，在不同彈體頭部阻力的影響下，各彈體的瞬時侵徹深度有所差異，截錐形和尖錐形彈體的侵徹時間相對較長，侵徹能力較卵形彈體好。

圖11 不同頭部形狀彈體速度與侵徹深度的關系Fig．11 Penetration velocity vs．penetration depth for different optimal projectiles

圖12 不同頭部形狀彈體以800m／s的初速度侵徹混凝土時加速度和瞬時侵徹深度時程曲線Fig．12 Curves of acceleration and instantaneous penetration depth for projectiles with different nose shapes penetrating into concrete at an initial velocity of 800m／s

4 結 論

基于局部相互作用模型思想，結合與彈體頭部形狀相關的開坑計算方法及歸一化彈體頭形方程，得到了任意頭部形狀彈體侵徹混凝土的侵徹深度計算模型，并通過實驗數據驗證了計算模型的有效性。在此基礎上，利用彈形優化最大侵深法，得到無量綱化彈體頭部形狀控制參數表達式及經典變分彈形優化方法，確定了典型的回轉形彈體頭部形狀控制參數最優值，并由優化結果得到了典型彈體的優化頭部形狀。采用彈靶分離方法進行模擬，對典型的優化頭部形狀彈體侵徹混凝土靶的侵徹深度進行對比分析，結果表明：（1）當彈體頭部相對半徑較小時，球頭錐形和球頭卵形彈體將分別優化為尖頭錐形和尖頭卵形彈體；（2）優化截頭彈體的侵徹深度大于優化尖頭彈體，優化截錐形彈體的侵徹深度最大；（3）優化彈體頭部形狀能有效地降低侵徹過程中的彈體阻力，提高彈體的侵徹深度。如何合理地優化彈體頭部形狀，開展基于局部相互作用模型的非回轉體復雜三維頭部形狀結構彈體的侵徹過程理論分析及彈形優化設計，使彈體在侵徹過程中達到更好的作用效能，將是下一步研究的重點。

參考文獻：

［1］ Bunimovich A I，Dubinskii A V．Mathematical models and methods of localized interaction theory［M］．Singapore：World Scientific Publishing，1995．

［2］ Ben－Dor G，Dubinsky A，Elperin T．Applied high－speed plate penetration dynamics［M］．Netherlands：Springer，2006．

［3］ Ben－Dor G，Dubinsky A，Elperin T．High－speed penetration dynamics：Engineering models and methods［M］．Singapore：World Scientific Publishing，2013．

［4］ Ben－Dor G，Dubinsky A，Elperin T．High－speed penetration modeling and shape optimization of the projectile penetrating into concrete shields［J］．Mechanics Based Design of Structures and Machines，2009，37（4）：538－549．

［5］ Ben－Dor G，Dubinsky A，Elperin T．Localized interaction models with non－constant friction for rigid penetrating impactors［J］．International Journal of Solids and Structures，2007，44（7）：2593－2607．

［6］ Ben－Dor G，Dubinsky A，Elperin T．Numerical solution for shape optimization of an impactor penetrating into a semi－infinite target［J］．Computers ＆Structures，2003，81（1）：9－14．

［7］ Ben－Dor G，Dubinsky A，Elperin T．Shape optimization of impactor penetrating into concrete or limestone targets［J］．International Journal of Solids and Structures，2003，40（17）：4487－4500．

［8］ Ben－Dor G，Dubinsky A，Elperin T．Optimization of the nose shape of an impactor against a semi－infinite FRP laminate［J］．Composites Science and Technology，2002，62（5）：663－667．

［9］ Ben－Dor G，Dubinsky A，Elperin T．Optimization of layered shields with a given areal density［J］．International Journal of Fracture，1998，91（1）：L9－L14．

［10］ Yakunina G E．The dynamics of pyramidal bodies within the framework of the local interaction model［J］．Journal of Applied Mathematics and Mechanics，2003，67（1）：11－23．

［11］ Yakunina G Y．The three－dimensional motion of optimalpyramidal bodies［J］．Journal of Applied Mathematics and Mechanics，2005，69（2）：234－243．

［12］ Yakunina G．Optimum three－dimensional hypersonic bodies within the framework of a local interaction model［C］∥10th AIAA／NAL－NASDA－ISAS International Space Planes and Hypersonic Systems and Technologies Conference，2001：11．

［13］ Yakunna G Y．Effects of sliding friction on the optimal 3D－nose geometry of rigid rods penetrating media［J］．Optimization and Engineering，2005，6（3）：315－338．

［14］ Ragnedda F，Serra M．Optimum shape of high speed impactor for concrete targets using PSOA heuristic［J］．Engineering，2010，2（4）：257－262．

［15］ Jones S E，Rule W K．On the optimal nose geometry for a rigid penetrator，including the effects of pressuredependent friction［J］．International Journal of Impact Engineering，2000，24（4）：403－415．

［16］ Chen X W，Li Q M．Deep penetration of a non－deformable projectile with different geometrical characteristics［J］．International Journal of Impact Engineering，2002，27（6）：619－637．

［17］ 皮愛國，黃風雷．基于變分法原理的侵徹彈體頭部形狀優化設計［J］．彈箭與制導學報，2007，27（4）：126－130．Pi Aiguo，Huang Fenglei．Based on variation method for the shape optimization of penetrator nose shape［J］．Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（4）：126－130．

［18］ 劉堅成，黃風雷，皮愛國，等．異型頭部彈體增強侵徹性能機理研究［J］．爆炸與沖擊，2014，34（4）：409－414．Liu Jiancheng，Huang Fenglei，Pi Aiguo，et al．On enhanced penetration performance of modified nose projectiles［J］．Explosion and Shock Waves，2014，34（4）：409－414．

［19］ Liu J，Pi A，Huang F．Penetration performance of double－ogive－nose projectiles［J］．International Journal of Impact Engineering，2015，84：13－23．

［20］ Forrestal M J，Tzou D Y．A spherical cavity－expansion penetration model for concrete targets［J］．International Journal of Solids and Structures，1997，34（31）：4127－4146．

［21］ Luk V K，Forrestal M J．Penetration into semi－infinite reinforced－concrete targets with spherical and ogival nose projectiles［J］．International Journal of Impact Engineering，1987，6（4）：291－301．

［22］ Li Q M，Chen X W．Dimensionless formulae for penetration depth of concrete target impacted by a non－deformable projectile［J］．International Journal of Impact Engineering，2003，28（1）：93－116．

［23］ Teland J A，Sjl H．Penetration into concrete by truncated projectiles［J］．International Journal of Impact Engineering，2004，30（4）：447－464．

［24］ 黃民榮．剛性彈體對混凝土靶的侵徹與貫穿機理研究［D］．南京：南京理工大學，2011．

［25］ Forrestal M J，Frew D J，Hickerson J P，et al．Penetration of concrete targets with deceleration－time measure－ments［J］．International Journal of Impact Engineering，2003，28（5）：479－497．

［26］ Qian L，Yang Y，Tong L．A semi－analytical model for truncated－ogive－nose projectiles penetration into semi－infinite concrete targets［J］．International Journal of Impact Engineering，2000，24（9）：947－955．

［27］ 石志勇，湯文輝，趙國民，等．混凝土靶中侵徹深度的相似性研究［J］．彈道學報，2005，17（1）：62－66．Shi Zhiyong，Tang Wenhui，Zhao Guomin，et al．Similarity study of the penetration depth for the concrete targets［J］．Journal of Ballistics，2005，17（1）：62－66．

［28］ Ben－Dor G，Dubinsky A，Elperin T．Shape optimization of high－speed penetrators：A review［J］．Central European Journal of Engineering，2012，2（4）：473－482．

［29］ Forrestal M J，Tzou D Y．A spherical cavity－expansion penetration model for concrete targets［J］．International Journal of Solids ＆Structures，1997，34（31）：4127－4146．

［30］ 何濤，文鶴鳴．卵形鋼彈對鋁合金靶板侵徹問題的數值模擬［J］．高壓物理學報，2006，20（4）：408－414．He Tao，Wen Heming．Numerical simulations of the penetration of aluminum targets by ogive－nosed steel projectiles［J］．Chinese Journal of High Pressure Physics，2006，20（4）：408－414．

［31］ Fang Q，Kong X，Hong J，et al．Prediction of projectile penetration and perforation by finite cavity expansion method with the free－surface effect［J］．Acta Mechanica Solida Sinica，2014，27（6）：597－611．

［32］ Li Q M，Flores－Johnson E A．Hard projectile penetration and trajectory stability［J］．International Journal of Impact Engineering，2011，38（10）：815－823．

Nose－shape optimization and simulation of projectiles penetrating into concrete target based on local interaction theory

Deng Jiajie1，Zhang Xianfeng1，2，Ge Xiankun1，3，Chen Dongdong1，Guo Lei1

（1．Ministerial Key Laboratory of ZNDY，Nanjing University of Science and Technology，Nanjing210094，Jiangsu，China；2．State Key Laboratory for Disaster Prevention ＆Mitigation of Explosion ＆Impact，PLA University of Science and Technology，Nanjing210007，Jiangsu，China；3．The Unit 95856 of PLA，Nanjing210000，Jiangsu，China）

Based on the local interaction theory，we proposed a penetration depth model for projectiles with an arbitrary nose－shape penetrating into a concrete target in consideration of the cratering stage related to nose－shape and normalized nose－shape function．Furthermore，using the method of maximum depth of penetration，we presented an expression about the normalized control parameter of the nose－shape and the classical variational optimization of the nose－shape．The local interaction model prediction and simulation results accord well with the experimental data of different projectile nose shapes．The optimal analysis and simulation show that，when the relative radius of the projectile nose is small，the optimal spherical－tip projectile is similar to corresponding optimal sharp－tip projectile，and the optimized truncated－tip projectiles have better penetration performance than that of the corresponding sharp－tip projectile．Compared with other nose－shaped projectiles，the optimized truncatedconical projectile has a relatively greater penetration depth．As the shape of the projectile nose affects its overload in the penetration process，the optimized shape of the projectile nose can effectively improve the penetration depth of the projectile．

penetration projectile；concrete target；local interaction model；nose－shape optimization of projectile

O385國標學科代碼：1303530

A

10．11883／1001－1455（2017）04－0611－10

（責任編輯 王 影）

2015－12－04；

2016－03－14

中共中央組織部青年拔尖人才支持計劃項目；爆炸沖擊防災減災國家重點實驗室（解放軍理工大學）開放基金項目（DPMEIKF201405）

鄧佳杰（1990－ ），男，博士研究生；通信作者：張先鋒，lynx＠njust．edu．cn。