火箭助推器翼傘回收動(dòng)力學(xué)仿真與試驗(yàn)分析

蔣萬(wàn)松 榮偉 滕海山 劉濤 李春

（北京空間機(jī)電研究所，北京 100094）

火箭助推器翼傘回收動(dòng)力學(xué)仿真與試驗(yàn)分析

蔣萬(wàn)松 榮偉 滕海山 劉濤 李春

（北京空間機(jī)電研究所，北京 100094）

翼傘具有良好的滑翔性、操縱性和穩(wěn)定性，能夠解決火箭助推器落點(diǎn)散布大導(dǎo)致的安全性問(wèn)題。為對(duì)翼傘回收系統(tǒng)和控制系統(tǒng)進(jìn)行優(yōu)化設(shè)計(jì)，以基于可控翼傘回收技術(shù)的火箭助推器-控制平臺(tái)—翼傘多體飛行系統(tǒng)為研究對(duì)象，采用拉格朗日乘子法建立了三體組合10自由度多體動(dòng)力學(xué)仿真模型，考慮了翼傘的表觀質(zhì)量特性和火箭助推器的氣動(dòng)力影響，對(duì)某次空投飛行試驗(yàn)進(jìn)行了動(dòng)力學(xué)過(guò)程仿真重建，通過(guò)仿真與試驗(yàn)的對(duì)比分析飛行機(jī)理和系統(tǒng)性能。分析結(jié)果表明，翼傘系統(tǒng)間存在多體相對(duì)運(yùn)動(dòng)，必須采用多體動(dòng)力學(xué)模型進(jìn)行研究；機(jī)動(dòng)飛行時(shí)，火箭助推器與翼傘間的相對(duì)運(yùn)動(dòng)角度并不大，而且火箭助推器的大尺寸對(duì)相對(duì)偏航運(yùn)動(dòng)的影響也并不顯著；航向跟蹤誤差主要來(lái)自操縱效率低，在小角度航向跟蹤誤差時(shí)，需提高操縱控制增益。研究成果可以為翼傘系統(tǒng)的工程設(shè)計(jì)與應(yīng)用提供參考。

翼傘 多體動(dòng)力學(xué) 拉格朗日乘子法 火箭助推器 航天回收

0 引言

隨著我國(guó)火箭發(fā)射活動(dòng)日益頻繁，火箭助推器殘骸及廢液等的回落對(duì)一些村莊與小鎮(zhèn)居民的生命和財(cái)產(chǎn)造成不同程度的威脅。目前，火箭及其分離體的回收技術(shù)已成為國(guó)內(nèi)研究熱點(diǎn)。

翼傘不僅像普通降落傘一樣折疊包裝方便、體積小和質(zhì)量輕，而且滑翔性、操縱性和穩(wěn)定性好，能夠解決火箭助推器落點(diǎn)散布大的問(wèn)題，在航空航天飛行器和分離體的精確定點(diǎn)回收方面有著很高的應(yīng)用價(jià)值，但目前國(guó)內(nèi)外尚無(wú)采用翼傘系統(tǒng)回收火箭助推器的先例。

針對(duì)火箭助推器的定點(diǎn)回收問(wèn)題，開(kāi)發(fā)了縮比質(zhì)量的翼傘回收系統(tǒng)，并進(jìn)行了空投飛行試驗(yàn)，如圖1（a）所示。系統(tǒng)由翼傘（包括傘衣、傘繩和吊帶等）、操縱控制系統(tǒng)和控制平臺(tái)（系統(tǒng)集成結(jié)構(gòu)）組成，操縱控制系統(tǒng)設(shè)備布置在控制平臺(tái)上，如圖1（b）所示，火箭助推器作為其有效載荷。在火箭發(fā)射時(shí)，翼傘系統(tǒng)折疊包裝在火箭助推器的頭錐部位。

為優(yōu)化系統(tǒng)總體設(shè)計(jì)和歸航控制律，對(duì)某次空投試驗(yàn)進(jìn)行了飛行過(guò)程動(dòng)力學(xué)仿真重建和機(jī)理分析。然而，翼傘系統(tǒng)與傳統(tǒng)航空飛行器不同，翼傘與有效載荷或控制平臺(tái)之間存在明顯相對(duì)運(yùn)動(dòng)，尤其是開(kāi)傘、轉(zhuǎn)彎?rùn)C(jī)動(dòng)或雀降機(jī)動(dòng)過(guò)程中更加明顯，要從多體系統(tǒng)動(dòng)力學(xué)的角度對(duì)翼傘-載荷系統(tǒng)進(jìn)行動(dòng)力學(xué)建模和分析；翼傘是一種超輕結(jié)構(gòu)，需要考慮翼傘的表觀質(zhì)量的影響；火箭助推器的外形對(duì)系統(tǒng)的影響尚不明確；試驗(yàn)表明翼傘的操縱響應(yīng)有較大的遲滯。本文在飛行過(guò)程動(dòng)力學(xué)建模時(shí)考慮了上述因素，并研究了響應(yīng)遲滯和載荷體外形氣動(dòng)力對(duì)系統(tǒng)性能的影響。

1 翼傘系統(tǒng)動(dòng)力學(xué)建模

本文主要研究火箭助推器翼傘回收系統(tǒng)從開(kāi)傘充氣張滿(mǎn)到著陸過(guò)程的動(dòng)力學(xué)行為。目前用于一般翼傘系統(tǒng)多體動(dòng)力學(xué)特性研究的仿真模型均將傘體和有效載荷分別看作兩個(gè)獨(dú)立的剛體，不同之處在于連接約束模型，歸納起來(lái)主要分為三類(lèi)：

第一類(lèi)是“兩體+彈簧”。兩體間通過(guò)彈簧相連，連接點(diǎn)的空間位置顯式求解，彈簧參數(shù)設(shè)置依賴(lài)于設(shè)計(jì)和經(jīng)驗(yàn)，增加了求解自由度且難于收斂；以文獻(xiàn)[1-3]等為代表。

第二類(lèi)是“兩體+約束方程”。兩體間通過(guò)約束方程建立關(guān)系，保證了連接點(diǎn)空間位置的一致性，建模過(guò)程程式化，便于模型的擴(kuò)展，但增加了求解自由度，以文獻(xiàn)[4-11]等為代表。

第三類(lèi)采用“共鉸點(diǎn)兩體+扭簧”。兩體間共用一個(gè)坐標(biāo)系原點(diǎn)，相對(duì)姿態(tài)關(guān)系通過(guò)扭簧建立關(guān)系，其參數(shù)的設(shè)置依賴(lài)于實(shí)際系統(tǒng)和仿真經(jīng)驗(yàn)，為最小解集系統(tǒng)，以文獻(xiàn)[12-15]等為代表。

1.1 基本假設(shè)

本文采用擴(kuò)展性好的拉格朗日乘子法對(duì)一般可控翼傘—控制平臺(tái)—載荷系統(tǒng)建立了三體10DOF（自由度）動(dòng)力學(xué)仿真模型，翼傘表觀質(zhì)量計(jì)算采用Barrows方法[16-17]，類(lèi)似的兩體8DOF模型已得到了驗(yàn)證[18]。在建立系統(tǒng)動(dòng)力學(xué)仿真模型時(shí)，做如下基本假設(shè)：

1）大地是水平的，忽略地球自轉(zhuǎn)，且重力加速度恒定；

2）翼傘完成充氣張滿(mǎn)后幾何形狀不變，左右對(duì)稱(chēng)，后緣操縱只影響氣動(dòng)力；

3）翼傘、控制平臺(tái)和火箭助推器均看作6DOF剛體，兩體間通過(guò)剛性吊帶連接約束；

4）控制平臺(tái)和火箭助推器的質(zhì)量特性恒定不變，但翼傘含有表觀質(zhì)量，且隨大氣密度變化；

5）火箭助推器的氣動(dòng)力模型簡(jiǎn)化為圓柱體擾流模型，忽略控制平臺(tái)的氣動(dòng)力影響。

1.2 坐標(biāo)系選用

1）坐標(biāo)系

慣性坐標(biāo)系：固定于地球表面的東-北-天坐標(biāo)系，坐標(biāo)原點(diǎn)在著陸目標(biāo)點(diǎn)地面位置，x軸指向當(dāng)?shù)貣|向，y軸指向當(dāng)?shù)乇毕颍瑉軸由右手定則確定；

翼傘坐標(biāo)系：固定翼傘上的本體坐標(biāo)系，坐標(biāo)原點(diǎn)位于翼傘等效c/4（c為平均氣動(dòng)弦長(zhǎng)），x軸在翼傘縱向?qū)ΨQ(chēng)面內(nèi)與平均氣動(dòng)弦線平行并指向開(kāi)口方向，z軸在翼傘縱向?qū)ΨQ(chēng)面上并與 x軸正交并指向上表面，y軸由右手定則確定，如圖1所示；

控制平臺(tái)坐標(biāo)系：固定在有效載荷平臺(tái)上的本體坐標(biāo)系，坐標(biāo)原點(diǎn)位于有效載荷平臺(tái)的質(zhì)心位置，x軸與穩(wěn)定飛行前方一致，z軸與x軸垂直并指向上方，y軸由右手定則確定；

有效載荷坐標(biāo)系：固定在火箭助推器上的本體坐標(biāo)系，坐標(biāo)原點(diǎn)位于火箭助推器的質(zhì)心位置，x軸指向頭錐，z軸與x軸垂直并處于吊點(diǎn)一側(cè)，y軸由右手定則確定，如圖1所示；

翼傘氣流坐標(biāo)系：坐標(biāo)原點(diǎn)位于翼傘等效c/4處，x軸指向氣流的來(lái)流方向，z軸在翼傘的縱向?qū)ΨQ(chēng)面內(nèi)且與x軸垂直，y軸由右手定則確定。

2）坐標(biāo)系間關(guān)系

從慣性坐標(biāo)系到本體坐標(biāo)系采用z-y-x轉(zhuǎn)序的歐拉角（偏航、俯仰和滾轉(zhuǎn)）來(lái)描述姿態(tài)，記為(ψ, θ, φ)，通過(guò)下角標(biāo)區(qū)分（翼傘為 p；控制平臺(tái)為 C；有效載荷為 B），慣性系到本體系的轉(zhuǎn)換矩陣定義[19]為S =Sx(φ) Sy(θ)Sz(ψ)，且有 S-1=ST其( )T為轉(zhuǎn)置矩陣。其中，

從氣流坐標(biāo)系到翼傘本體坐標(biāo)系采用z-y-x轉(zhuǎn)序的攻角α和側(cè)滑角β來(lái)描述，氣流系到本體系的轉(zhuǎn)換矩陣定義[19]為 Sa=Sy(- α) Sz(β)。

1.3 系統(tǒng)動(dòng)力學(xué)方程

翼傘系統(tǒng)中，翼傘、控制平臺(tái)和火箭助推器各看作6DOF剛體，多體系統(tǒng)動(dòng)力學(xué)方程為

式中 q為廣義坐標(biāo)；˙q為廣義速度；λ為拉格朗日乘子；Q為廣義力；f為約束方程向量；T為系統(tǒng)動(dòng)能，表示為

式中 M為質(zhì)量矩陣；J為慣量矩陣；H為慣量交叉矩陣；S本體系到慣性系的坐標(biāo)轉(zhuǎn)換矩陣；ω為本體角速度；ix為慣性系下位置；i˙x為慣性系下速度。

根據(jù)方程（1），三體系統(tǒng)的動(dòng)力學(xué)方程可以表示為

即式（3）簡(jiǎn)寫(xiě)為

式中 轉(zhuǎn)換矩陣 STT=diag(Sp,E, SC,E, SB,E)，為氣動(dòng)力；L?為氣動(dòng)力矩；E為單位矩陣；V為本體系下平動(dòng)速度，

下面給出方程（4）的約束方程及拉格朗日乘子的求解方法。翼傘系統(tǒng)多體間的約束模型可以看作一個(gè)復(fù)合約束副，如圖2所示。其中，A1和A2代表翼傘連接點(diǎn)；A0為A1A2的中點(diǎn)，在翼傘縱向?qū)ΨQ(chēng)面內(nèi)；B1和B2代表控制平臺(tái)的2個(gè)上連接點(diǎn)；B0為B1B2的中點(diǎn)，在控制平臺(tái)縱向?qū)ΨQ(chēng)面內(nèi)；C1，C2，C3和C4為控制平臺(tái)4個(gè)下連接點(diǎn)；D1和D2為助推器上兩個(gè)連接點(diǎn)。

1）翼傘—控制平臺(tái)的連接特征線A0B0與B1B2（平行于控制平臺(tái)y軸）正交，即約束f1

式中 ε=（- s in θ,0,-cosθ ）T； θ為翼傘安裝角； e ( j=1,2,3)為單位矢量基，滿(mǎn)足 E =(e, e, e )。

2）翼傘—控制平臺(tái)連接特征線A0B0總是在翼傘縱向?qū)ΨQ(chēng)面內(nèi)，但沿A0B0線可移動(dòng)，即f2和f3分別為

式中 rB0為B0點(diǎn)在控制平臺(tái)本體坐標(biāo)系下的位置向量。

3）翼傘—控制平臺(tái)間沿A0B0線移動(dòng)受單個(gè)吊帶長(zhǎng)度約束，假設(shè)其不發(fā)生變化，即f4表示為

式中 rA1和 rB1分別為連接吊索兩端點(diǎn)在翼傘和控制平臺(tái)坐標(biāo)系下的向量；l1為連接吊索長(zhǎng)度。

4）控制平臺(tái)與有效載荷間約束與式（7）和式（8）類(lèi)似，即f5～ f8表示為

式中1Dr ，2Dr ，2Cr 和3Cr 為連接吊索兩端點(diǎn)在有效載荷和控制平臺(tái)本體坐標(biāo)系下向量；l2和 l3為控制平臺(tái)與有效載荷（助推器）間連接吊索長(zhǎng)度，如圖2所示。

為得到方程（1）第三項(xiàng)，并直接求解出拉格朗日乘子，對(duì)約束方程f求導(dǎo)

式中 拉格朗日方程廣義坐標(biāo) q =（xip,θp,xiC,θC,xiB,θB）T；=（Vp, ωp, VC,ωC, VB,ωB）T為本體系下表達(dá)的廣義速度； f=(f1, f2,f3, f4,f5, f6, f7,f8)T為約束方程；N為約束方程對(duì)本體系廣義速度的導(dǎo)數(shù)矩陣；K為余項(xiàng)列陣。

式中 S =STS； S =STS ； S˙ =S ω×-ω×S ； S˙ =S ω×-ω×S ；( )×為反對(duì)稱(chēng)矩陣。1Cp2 BC 11pC122CB2ρ x S r x S r ；Br和Cr分別為ρ x S r x S r；121CCpp= + --i BiA11ρ x S r x S r ；232 BBCC= + --i DiC3BBCC= + --i DiC單根吊帶兩端點(diǎn)在載荷和控制平臺(tái)本體坐標(biāo)系下的位置向量；

應(yīng)用式（4）和式（13），可求解出拉格朗日乘子

從而最終得到的系統(tǒng)動(dòng)力學(xué)方程為

以上方程可通過(guò)通常數(shù)值積分方法進(jìn)行求解。

1.4 表觀質(zhì)量估算

本文所述翼傘沿展向展開(kāi)后為矩形的圓弧形翼傘，采用Barrows估算方法[16]給出的翼傘的表觀質(zhì)量矩陣如式（18）所示，計(jì)算時(shí)加到方程（3）中與翼傘相關(guān)質(zhì)量項(xiàng)中。

=0.055；*h為翼傘比高度（翼傘頂點(diǎn)到翼傘兩側(cè)邊緣的高度與展長(zhǎng)之比）；b為翼傘展長(zhǎng)；c為翼傘弦長(zhǎng)；w為傘繩匯聚點(diǎn)；0e為翼型剖面百分比厚度；下標(biāo)k為俯仰中心；下標(biāo)r為滾動(dòng)中心；γ為展弦比；kA和kB為系數(shù)；aρ為大氣密度；R0為系統(tǒng)長(zhǎng)度；SA=bc為翼傘參考面積。

1.5 氣動(dòng)模型

翼傘氣動(dòng)力計(jì)算采用經(jīng)典飛行力學(xué)方法，計(jì)算式及相關(guān)氣動(dòng)系數(shù)如表1所示。升阻力氣動(dòng)系數(shù)參考了 lingard[20]文獻(xiàn)，靜導(dǎo)數(shù)系數(shù)和橫向氣動(dòng)參數(shù)參考了 Prakash[13]和 Iacomini[21]文獻(xiàn)，瞬時(shí)飛行狀態(tài)大氣密度（GJB 365.1-1987）和氣動(dòng)參數(shù)均通過(guò)樣條插值計(jì)算。

表1 翼傘氣動(dòng)力模型Tab.1 Aerodynamic model for parafoil

在考慮有效載荷氣動(dòng)力時(shí)，將火箭助推器簡(jiǎn)化為圓柱體擾流模型，不考慮兩端圓形端面的氣動(dòng)力，圓柱面受到氣動(dòng)阻力和氣動(dòng)升力作用，如圖2所示，采用經(jīng)典飛行力學(xué)計(jì)算方法，主要與來(lái)流總攻角有關(guān)，阻力系數(shù)和升力系數(shù)如圖3所示[22]。

1.6 歸航控制律說(shuō)明

翼傘系統(tǒng)完整的飛行過(guò)程包括定向飛行段、盤(pán)旋管理段、逆風(fēng)調(diào)整段和雀降機(jī)動(dòng)段。定向飛行段根據(jù)翼傘系統(tǒng)的當(dāng)前位置及目標(biāo)落點(diǎn)位置，自動(dòng)調(diào)整航向，使系統(tǒng)向著目標(biāo)點(diǎn)飛行；盤(pán)旋管理段在落點(diǎn)的目標(biāo)上空進(jìn)行盤(pán)旋機(jī)動(dòng)，對(duì)飛行高度進(jìn)行管理，使之在落點(diǎn)上空附近飛行；逆風(fēng)調(diào)整段根據(jù)當(dāng)前飛行高度、位置、風(fēng)向等信息，計(jì)算欲落點(diǎn)位置，并在該段結(jié)束時(shí)使系統(tǒng)飛至預(yù)落點(diǎn)位置，且飛行方向處于逆風(fēng)飛行狀態(tài)；雀降機(jī)動(dòng)段通過(guò)雙邊操縱制動(dòng)實(shí)施精確軟著陸。

本文采用具有基準(zhǔn)下偏量的簡(jiǎn)單線性下偏操縱歸航控制律，即翼傘后緣下偏量輸出量指令與航向偏差量 Δψ 成正比關(guān)系，如表2所示。其中h(t)和R(t)分別為系統(tǒng)在任意時(shí)刻t，離目標(biāo)點(diǎn)高度和水平距離，h1、h2、R1和R2為模式轉(zhuǎn)換設(shè)置的定值，下標(biāo)m和n分別表示翼傘左、右后緣。

根據(jù)事先預(yù)置或地面通過(guò)遙控上傳的風(fēng)向數(shù)據(jù)（優(yōu)先級(jí)高于計(jì)算值），計(jì)算實(shí)際航向與風(fēng)向的夾角Δψ 。飛行試驗(yàn)中，逆風(fēng)調(diào)整段和雀降著陸段因地著陸點(diǎn)高度偏差沒(méi)有實(shí)施。

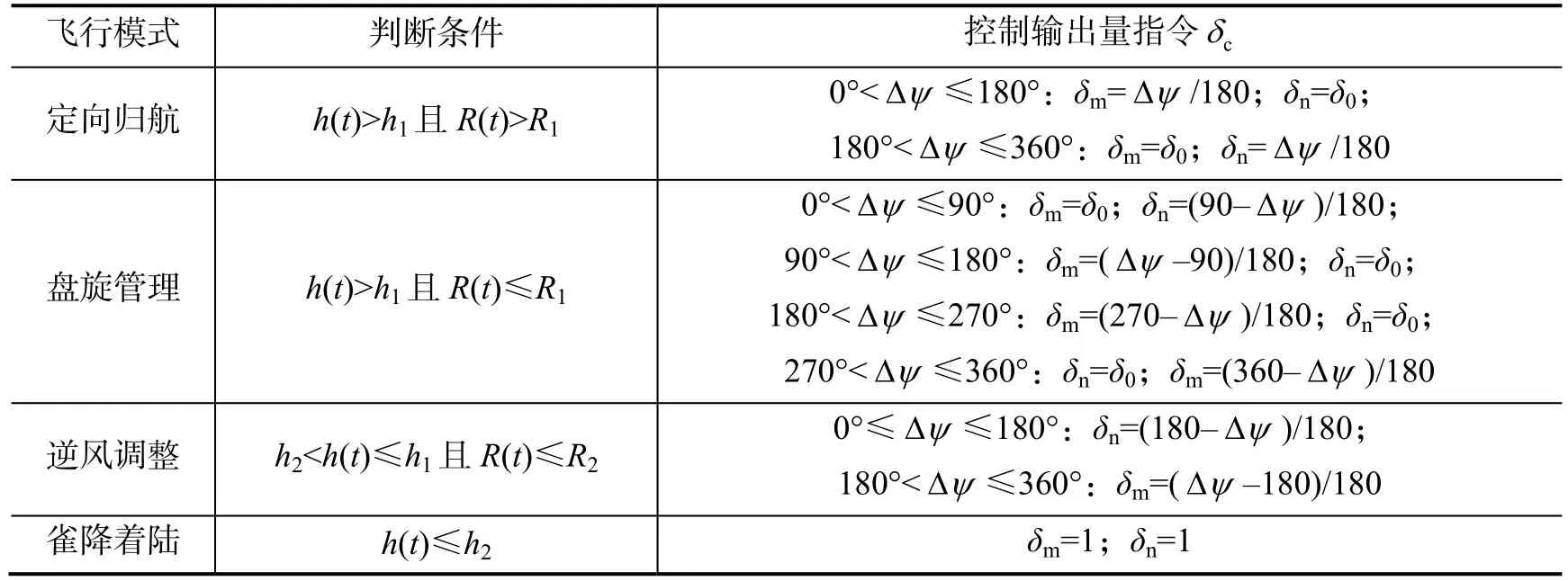
表2 各飛行模式歸航控制算法Tab.2 Homing control algorithm in all types of flight modes

1.7 操縱響應(yīng)延遲模型

翼傘操縱機(jī)構(gòu)對(duì)操縱控制指令執(zhí)行需要一定的響應(yīng)時(shí)間，大型翼傘更加明顯，長(zhǎng)達(dá)數(shù)秒。動(dòng)力學(xué)建模時(shí)有必要考慮操縱響應(yīng)的延遲，建立與操縱率和操縱指令有關(guān)的簡(jiǎn)單模型

式中max˙ 為最大操縱速率；Δt為步長(zhǎng)；cδ 根據(jù)表2計(jì)算得到。

2 動(dòng)力學(xué)仿真

2.1 仿真條件說(shuō)明

翼型Clark-Y，弦長(zhǎng)5.55m，翼展14.4m，厚度0.15m，系統(tǒng)長(zhǎng)度11.5m，安裝角6°（不含剖面4°），翼傘凈質(zhì)量35kg；助推器模型長(zhǎng)5.6m，直徑0.9m，質(zhì)量800kg，重心距噴口1.8m；航向定義為東偏北為正，角度范圍為（-180°,180°）。

仿真初始條件：東向477m，北向1 002m，高度3 980m，航向-160°，飛行時(shí)間258s，盤(pán)旋半徑550m，無(wú)風(fēng)。著陸目標(biāo)點(diǎn)（0,0,1 575）。

2.2 仿真與試驗(yàn)結(jié)果對(duì)比

仿真與試驗(yàn)結(jié)果的對(duì)比如圖4所示。

2.3 結(jié)果分析

通過(guò)以上仿真與試驗(yàn)結(jié)果的對(duì)比，經(jīng)分析得到以下基本結(jié)論：

從圖 4（a）和（b）可以看出，翼傘系統(tǒng)整體上至少經(jīng)歷了定向飛行和盤(pán)旋管理段，是經(jīng)過(guò)飛行模式轉(zhuǎn)變的復(fù)合運(yùn)動(dòng)。從圖4（c）看出，翼傘系統(tǒng)的下降速度基本穩(wěn)定在一個(gè)恒值，約9.5m/s；仿真得到的水平速度與試驗(yàn)結(jié)果有所差別，仿真結(jié)果是逐漸減小的，約20～23m/s，而試驗(yàn)測(cè)得水平速度有波動(dòng)，系統(tǒng)滑翔比為2.2左右；結(jié)合圖4（d），水平速度與操縱量存在關(guān)聯(lián)性。圖4（d）中仿真得到的操縱量比試驗(yàn)記錄的操縱量略小，試驗(yàn)曲線沒(méi)有體現(xiàn)定向飛行到盤(pán)旋管理段的轉(zhuǎn)換過(guò)程，而仿真結(jié)果在60～70s左右出現(xiàn)了零操縱狀態(tài)到50%操縱量峰值突變，明顯體現(xiàn)了該轉(zhuǎn)換過(guò)程。

圖5給出了仿真分析結(jié)果，包括氣流角、姿態(tài)角和相對(duì)姿態(tài)角。圖示均表明了在60～70s出現(xiàn)了飛行模式轉(zhuǎn)變，攻角、側(cè)滑角、俯仰角、滾轉(zhuǎn)角及相對(duì)俯仰角和滾轉(zhuǎn)角均有所變化，在進(jìn)入盤(pán)旋管理段后趨于穩(wěn)定。圖 5（c）和（d）中，翼傘與平臺(tái)間存在相對(duì)運(yùn)動(dòng)，在機(jī)動(dòng)時(shí)表現(xiàn)得比較明顯，說(shuō)明系統(tǒng)間存在相對(duì)運(yùn)動(dòng)，但是角度比較小，進(jìn)一步說(shuō)明了采用多體動(dòng)力學(xué)仿真模型的必要性，也說(shuō)明至少應(yīng)采用 7或8自由度以上的模型才能較真實(shí)反映物理過(guò)程。從圖5（c）初步得到，火箭助推器的大尺寸對(duì)相對(duì)偏航運(yùn)動(dòng)的影響并不大。

結(jié)合歸航控制律和飛行過(guò)程，定向飛行階段存在大角度的跟蹤誤差，始終沒(méi)有朝向目標(biāo)點(diǎn)（原點(diǎn)），以致于定向飛行到盤(pán)旋管理段的過(guò)度過(guò)程比較平緩，但按照控制律邏輯應(yīng)有明顯的界限，原因可能是轉(zhuǎn)彎操縱控制效率低、較大的相對(duì)偏航運(yùn)動(dòng)或航向測(cè)量誤差。從仿真結(jié)果來(lái)看，翼傘與控制平臺(tái)間的相對(duì)偏航運(yùn)動(dòng)較小（＜4°）；航向測(cè)量誤差不超過(guò)±10°，都不是航向跟蹤誤差的主因，因此航向大角度跟蹤誤差更可能是轉(zhuǎn)彎操縱控制效率低導(dǎo)致，這就要求在小角度航向誤差時(shí)，增大操縱控制增益，但同時(shí)需改進(jìn)航向飛行到盤(pán)旋管理段的過(guò)度過(guò)程控制律。

3 結(jié)束語(yǔ)

本文針對(duì)火箭助推器翼傘回收多體飛行動(dòng)力學(xué)系統(tǒng)為研究對(duì)象，采用拉格朗日乘子法建立了三體10DOF動(dòng)力學(xué)仿真模型，考慮了翼傘的表觀質(zhì)量特性。對(duì)某次空投飛行試驗(yàn)過(guò)程進(jìn)行了動(dòng)力學(xué)仿真重建，驗(yàn)證了仿真模型的有效性，分析了飛行過(guò)程機(jī)理和性能，提出小角度操縱時(shí)應(yīng)增大操縱控制增益。

References)

[1]VISHNYAK A. Simulation of the Payload-parachute-wing System Flight Dynamics[C]//Aerospace Design Conference, Irvine, CA, U.S.A. AIAA 93-1250.

[2]熊菁. 翼傘系統(tǒng)動(dòng)力學(xué)與歸航方案研究[D]. 長(zhǎng)沙： 國(guó)防科技大學(xué)博士學(xué)位論文, 2005. XIONG Jing. Research on Dynamics and Homming Control of Parafoil System[D]. Changsha： National University of DefenseTechnology, 2005. (in Chinese)

[3]熊菁, 宋旭民, 秦子增. 翼傘系統(tǒng)兩體相對(duì)運(yùn)動(dòng)分析[J]. 航天返回與遙感, 2004, 25(2)： 10-16. XIONG Jing, SONG Xuming, QIN Zizeng. Study on Relative Motion of Two-body Parafoil System[J]. Spacecraft Recovery & Remote Sensing, 2004, 25(2)： 10-16. (in Chinese)

[4]YAKIMENKO O A. On the Development of a Scalable 8-DOF Model for a Generic Parafoil-payload Delivery System[C]// 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany. AIAA 2005-1665.

[5]PILLASCH D W, SHEN Y C, VALERO N. Parachute/Submunition System Coupled Dynamics[C]//8th Aerodynamic Decelerator and Balloon Technology Conference, Hyannis, MA, U.S.A. AIAA 84-0784.

[6]WISE K A. Dynamics of a UAV with Parafoil under Powered Flight[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, Colorado. AIAA 2006-6795.

[7]STRICKER G, WITTE L. Analysis of the Relative Motion in a Parafoil-load System[C]//16th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Boston, MA, U.S.A. AIAA 2001-2013.

[8]CHRISTIAAN R. A Flight Simulation Algorithm for a Parafoil Suspending an Air Vehicle[J]. Journal of Guidance, Control and Dynamics, 2007, 30(3)： 791-803.

[9]MOOIJ E, WIJNANDS Q G, et al. 9 DOF Parafoil/ Payload Simulator Development and Validation[C]//AIAA Modeling and Simulation Technologies Conference and Exhibit, Austin, Texas. AIAA 2003-5459.

[10]陳建平, 寧雷鳴, 張紅英, 等. 基于多體動(dòng)力學(xué)的大型翼傘系統(tǒng)飛行仿真分析[J]. 飛行力學(xué), 2015, 33(6)： 486-490. CHEN Jianping, NING Leiming, ZHANG Hongying, et al. Flight Simulation and Analysis of Large Parafoil System Based on Multibody Dynamics[J]. Flight Dynamics, 2015, 33(6)： 486-490. (in Chinese)

[11]陳建平, 張紅英, 童明波, 等. 翼傘系統(tǒng)縱向飛行性能仿真[J]. 中國(guó)空間科學(xué)技術(shù), 2015, 35(2)： 25-32. CHEN Jianping, ZHANG Hongying, TONG Mingbo, et al. Longitudinal Flight Performances Simulation for Parafoil System[J]. Chinese Space Science and Technology, 2015, 35(2)： 25-32. (in Chinese)

[12]BARROWS T M. Multibody Parafoil Model[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Seattle, Washington. AIAA 2009-2945.

[13]PRAKASH O, ANANTHKRISHNAN N. Modeling and Simulation of 9-DOF Parafoil-payload System Flight Dynamics[C]// AIAA Atmospheric Flight Mechanics Conference and Exhibit, Keystone, Colorado. AIAA 2006-6130.

[14]MULLER S, WAGNER O, SACHS G. A High-fidelity Nonlinear Multibody Simulation Model for Parafoil System[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Monterey, California. AIAA 2003-2120.

[15]GORMAN C M, SLEGERS N J. Comparison and Analysis of Multi-body Parafoil Models with Varying Degrees of Freedom[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland. AIAA 2011-2615.

[16]BARROWS T M. Apparent Mass of Parafoils with Spanwise Camber[C]//16th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Boston, MA, U.S.A. AIAA 2001-2006.

[17]LISSAMAN B S, BROWN G J. Apparent Mass Effects on Parafoil Dynamics[C]//Aerospace Design Conference, Irvine, CA, U.S.A. AIAA 93-1236.

[18]蔣萬(wàn)松, 榮偉, 滕海山, 等. 翼傘載荷系統(tǒng)多體動(dòng)力學(xué)仿真分析[J]. 南京航空航天大學(xué)學(xué)報(bào), 2016, 48(4)： 474-481. JIANG Wansong, RONG Wei, TENG Haishan, et al. Multibody Dynamical Simulation Analysis for Parafoil-payload System[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(4)： 474-481. (in Chinese)

[19]趙育善, 師鵬. 航天器飛行動(dòng)力學(xué)建模理論與方法[M]. 北京： 北京航空航天大學(xué)出版社, 2012. ZHAO Yushan, SHI Peng. Spacecraft Flight Dynamics Modeling Theory and Methods[M]. Beijing： Beijing University of Aeronautics & Astronautics Press, 2012. (in Chinese)

[20]LINGARD J S. Ram Airparachute Design[C]//13th AIAA Aerodynamic Decelerator Systems Technology Conference, Clearwater Beach. AIAA 1995.

[21]IACOMINI C S, CERIMELE C J. Lateral-directional Aerodynamics from a Large Scale Parafoil Test Program[C]//15th Aerodynamic Decelerator Systems Technology Conference, Toulouse, France. AIAA 99-1731.

[22]夏雪湔, 鄧學(xué)鎣. 工程分離流動(dòng)力學(xué)[M]. 北京： 北京航空航天大學(xué)出版社, 1991. XIA Xuejian, DENG Xueying. Engineering Separation Flow Dynamics[M]. Beijing： Beijing University of Aeronautics & Astronautics Press, 1991. (in Chinese)

Dynamical Simulation and Test Analysis for Booster Recovery with Parafoil System

JIANG Wansong RONG Wei TENG Haishan LIU Tao LI Chun
（Beijing Institute of Space Mechanics and Electricity, Beijing 100094, China）

Controllable parafoil system could solve the security problem resulted from large dispersion of deserted boosters with its favorable gliding, manueverability and stability. To optimize the parafoil recovery system and its control system, taking a multibody dynamic system of booster-controller-parafoil based on parafoil recovery technology as a researching object, a three-body simulation model with 10-degree-of-freedom is established with Lagrange multiplier method, which considers the apparent mass characteristics of parafoil and aerodynamic impact of the booster. The process of an airdrop test is reconstructed with this model, and flight mechanism and performances are analyzed. The results show that multibody relative motion does exist among parafoil-payload systems, thus it is essential to establish a mutltibody model for simulation. While in maneuvering, the relative attitudes are not so large, and the aerodynamic of large size of rocket on parafoil system is not so profound. The tracking errors mainly come from low steering efficiency of parafoil, thus it is necessary to increase the gain of steering. The results provide a reference for the parafoil system engineering and application.

parafoil; multibody dynamics; Lagrange multiplier method; booster; spacecraft recovery

V275

A

1009-8518(2017)03-0013-11

10.3969/j.issn.1009-8518.2017.03.002

蔣萬(wàn)松，男，1981年生，2010年獲中國(guó)空間技術(shù)研究院飛行器設(shè)計(jì)專(zhuān)業(yè)碩士學(xué)位，高級(jí)工程師，中國(guó)空間技術(shù)研究院博士在讀。研究方向?yàn)楹教旆祷嘏c著陸技術(shù)。E-mail： skylingy24@sina.com。

（編輯：劉穎）

2017-03-20