基于蒙特卡洛有限元算法的建筑節(jié)約用材研究?

申琳 李曉剛

（1.楊凌職業(yè)技術(shù)學(xué)院楊凌712100）（2.西安協(xié)鑫新能源管理有限公司西安733000）

基于蒙特卡洛有限元算法的建筑節(jié)約用材研究?

申琳1李曉剛2

（1.楊凌職業(yè)技術(shù)學(xué)院楊凌712100）（2.西安協(xié)鑫新能源管理有限公司西安733000）

針對(duì)建筑用材在現(xiàn)實(shí)生活中過度消耗的問題，該研究以建筑結(jié)構(gòu)節(jié)約用材為切入點(diǎn)，深入分析結(jié)構(gòu)荷載可靠性指標(biāo)，通過攝動(dòng)有限元算法結(jié)合隨機(jī)場效應(yīng)在計(jì)算可靠性指標(biāo)的基礎(chǔ)上，構(gòu)建了解決建筑節(jié)約用料的蒙特卡洛有限元算法。利用Hasofer迭代和Orthogonal變換分別優(yōu)化功能函數(shù)和隨機(jī)變量轉(zhuǎn)換，將標(biāo)準(zhǔn)正態(tài)變量空間與中心原點(diǎn)距離最小值的點(diǎn)作為算法的核心，給出了節(jié)約條件下建筑用材的結(jié)構(gòu)可靠性求解。通過建筑過程中的梁可靠度進(jìn)行分析，結(jié)果表明：該研究提出的算法在隨機(jī)參數(shù)較小的條件下，建筑結(jié)構(gòu)強(qiáng)度仍具有可靠性，對(duì)減少建筑用材的需求具有參考性。

有限元算法；蒙特卡洛方法；建筑用料；結(jié)構(gòu)可靠性；節(jié)約用材

Class NumberTP391.7

1 引言

隨著計(jì)算機(jī)技術(shù)的迅速發(fā)展，建筑節(jié)約用材及其帶動(dòng)的數(shù)據(jù)分析量在不斷擴(kuò)大。建筑材料是建筑業(yè)建設(shè)的物質(zhì)基礎(chǔ)保障，并且眾多的原材料作為不可再生資源令我國耗材巨大。為了解決建筑節(jié)能設(shè)計(jì)，利用計(jì)算機(jī)技術(shù)與軟件信息對(duì)建筑設(shè)計(jì)起到了至關(guān)重要的輔助功能［1］。目前常用的建筑輔助軟件有建筑信息模型（BIM）［2］、計(jì)算機(jī)輔助建筑設(shè)計(jì)（CAAD）［3］和谷歌草圖大師（Google Sketchup）［4］等。同時(shí)，計(jì)算機(jī)技術(shù)處理建筑節(jié)約用材主要運(yùn)用了DTAC算法［5］、遺傳算法［6］和粒子群算法［7］等。本研究以有限元算法為主線，利用建筑結(jié)構(gòu)勢能泛函數(shù)、極限狀態(tài)分別分析了結(jié)構(gòu)隨機(jī)參數(shù)、結(jié)構(gòu)可靠性，將隨機(jī)場加入到模型中，結(jié)合攝動(dòng)隨機(jī)有限元法和可靠指標(biāo)共同建立蒙特卡洛有限元優(yōu)化迭代算法求解建筑節(jié)約用材可靠指標(biāo)。該算法重點(diǎn)分析了建筑節(jié)約用材后的可靠性，為集約化建筑用料提供改了計(jì)算參考意義。

2 蒙特卡洛有限元算法

2.1 攝動(dòng)隨機(jī)有限元法

利用建立在隨機(jī)場的S(x，θ)，對(duì)滿負(fù)結(jié)構(gòu)荷載以及充滿彈性參數(shù)的模量進(jìn)行處理［8］，并通過采用空間離散的方法，對(duì)隨機(jī)場S(x，θ)內(nèi)的隨機(jī)變量S=[S1，S2，…，SM]T實(shí)行轉(zhuǎn)化。利用變分法［9］，同時(shí)在構(gòu)建結(jié)構(gòu)勢能泛函數(shù)的開始就將結(jié)構(gòu)隨機(jī)參數(shù)以隨機(jī)性的方式加入到模型之中，從而來構(gòu)建隨機(jī)有限元法控制方程，構(gòu)建的方程如下：

在上述方程中，K-，a-和P-分別表示隨機(jī)矩陣K，a和P在均值S-處的值，Ki，ai和Pi分別表示K，a和P對(duì)Si的一階偏導(dǎo)數(shù)在S-處之值。

2.2 結(jié)構(gòu)可靠性

對(duì)結(jié)構(gòu)的可靠性進(jìn)行分析的過程中，我們能夠利用功能函數(shù)Z對(duì)結(jié)構(gòu)的極限狀態(tài)進(jìn)行描述［10］，這樣的情況下將會(huì)影響自變量，當(dāng)結(jié)構(gòu)工作中的基礎(chǔ)隨機(jī)變量成為自變量，Z可寫為

在上述的函數(shù)中，S表示在建筑結(jié)構(gòu)中施工過程以及使用材料的過程中幾何參數(shù)、材料參數(shù)以及荷載參數(shù)等變量。關(guān)于建筑過程中的結(jié)構(gòu)可將其定義為［11］

在上述的公式中，σz以及Z-分別表示功能函數(shù)Z的標(biāo)準(zhǔn)差和均值。

2.3 優(yōu)化迭代算法

從優(yōu)化迭代算法的角度來看，可以從幾何意義的角度出發(fā)來對(duì)結(jié)構(gòu)可靠的指標(biāo)進(jìn)行求解。在標(biāo)準(zhǔn)的正態(tài)隨機(jī)變量空間中，隨機(jī)變量的幾何意義代表著極限狀態(tài)曲面到坐標(biāo)原點(diǎn)之間距離的最小值。因此，在標(biāo)準(zhǔn)的正態(tài)隨機(jī)變量空間中［12］，獲得可靠指標(biāo)的途徑，需要通過在功能函數(shù)面G(x)上找到與坐標(biāo)原點(diǎn)之間距離最小值的點(diǎn)P*。而實(shí)際上，對(duì)于尋找的點(diǎn)P*是一個(gè)優(yōu)化的問題：

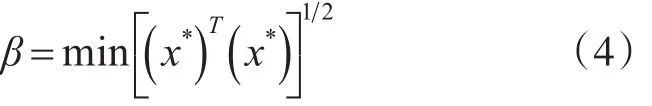
在上述的公式中，x*=(x1*，x*2，…，x*n)代表著功能函數(shù)Z面上的隨機(jī)驗(yàn)算點(diǎn)。通過Hasofer的優(yōu)化迭代算法進(jìn)行采用后［13］，還需要對(duì)式（4）進(jìn)行求解。通過式（5）的方法，能夠得出驗(yàn)算點(diǎn)x*的位置：

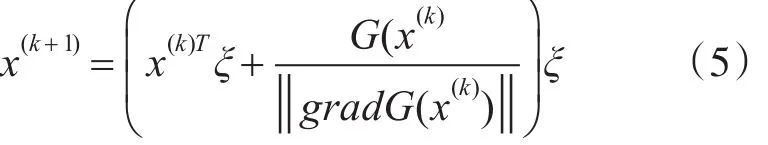
如上所示，x(k+1)表示第k+1次的優(yōu)化迭代算法而計(jì)算得到的驗(yàn)算點(diǎn)，‖gradG(x(k))‖和gradG(x(k))則分別代表著由第k次優(yōu)化迭加而計(jì)算出的功能函數(shù)的范數(shù)以及梯度，而ξ則表明了迭代中驗(yàn)算點(diǎn)移動(dòng)的總體方向。

3 建筑節(jié)約用材可靠性指標(biāo)

3.1 梯度函數(shù)求解

人們常用的RMCS方式主要是通過分析抽樣的方法來對(duì)一些可靠的指標(biāo)數(shù)據(jù)進(jìn)行獲取［14］，而本文選取的優(yōu)化迭代算法是建立在攝動(dòng)隨機(jī)有限元法求解的方法上對(duì)可靠指標(biāo)進(jìn)行獲取。本文選取的優(yōu)化迭代算法之所以能夠?qū)崿F(xiàn)與攝動(dòng)隨機(jī)有限元法相結(jié)合，其最為關(guān)鍵的原因在于，根據(jù)前部分提出的式（5），在得知隨機(jī)有限元法控制方程的情況下很容易推算出式子中的梯度向量gradG(x(k))。一般情況下得到的信息僅僅限于一些僅能夠表現(xiàn)出變量結(jié)構(gòu)的隨機(jī)變量S，而實(shí)際上并不能通過在非標(biāo)準(zhǔn)的空間下對(duì)處于非正態(tài)分布的隨機(jī)變量空間的隨機(jī)變量進(jìn)行推算，因此能夠得出gradG(x(k))為

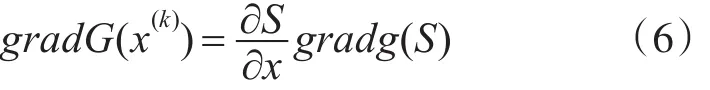
對(duì)于一般難以用隨機(jī)變量進(jìn)行表達(dá)的功能函數(shù)g(S)，無法直接通過推理和計(jì)算的方式來對(duì)梯度gradg(S)進(jìn)行求解。而在我們研究的對(duì)象轉(zhuǎn)為力學(xué)的時(shí)候，在力學(xué)特性的基礎(chǔ)上將可以對(duì)功能函數(shù)進(jìn)行劃分，將其中的隨機(jī)變量劃分為結(jié)構(gòu)抗力R以及隨機(jī)變量S等兩類與作用效應(yīng)F有關(guān)類別。根據(jù)上述的描述，可以得到如下的功能函數(shù)的梯度為

式（7）中，gR，gF代表中間變量R，F(xiàn)的梯度向量，JR，JF分別表示R，F(xiàn)的Jacobi矩陣。對(duì)于無法解決S顯式表示的結(jié)構(gòu)隨機(jī)響應(yīng)F，我們能夠利用Jacobi矩陣來進(jìn)行求解，但是在整體過程中，求解JF的過程非常繁雜。相對(duì)來說gF以及JR，gR都是比較容易求解得出的。這幫助了我們來確定下一步，即需要確定JF的第i行的轉(zhuǎn)置是隨機(jī)響應(yīng)F的一階偏導(dǎo)數(shù)，因此取結(jié)點(diǎn)位移為{ai}時(shí)能夠得到下式

3.2 變量變換

對(duì)于一階偏導(dǎo)數(shù)?S/?x的確定，首先需要確定的就是隨機(jī)變量S如何進(jìn)行處理的問題，首先將采取Orthogonal的變換［15］，在利用正交變換的方法得出非相關(guān)隨機(jī)變量Y：

上式中的A是通過正交規(guī)范化特征向量形成的矩陣，再將Y進(jìn)行標(biāo)準(zhǔn)化處理，得出非相關(guān)性的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量X：

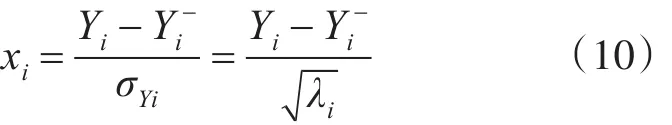
上式中，Y-i，σYi代表著Yi的均值和標(biāo)準(zhǔn)差。

3.3 算法求解流程

將優(yōu)化迭代算法以及攝動(dòng)隨機(jī)有限元法的方法相結(jié)合，計(jì)算出標(biāo)準(zhǔn)正態(tài)變量空間與中心原點(diǎn)距離最小值的點(diǎn)，這種基于驗(yàn)算點(diǎn)的迭代算法記為RPSFEM1。其具體的步驟如下：

Step1：首先需要將隨機(jī)場進(jìn)行離散處理，離散成為隨機(jī)變量S，同時(shí)計(jì)算出S的協(xié)方差矩陣CS，此時(shí)還需要計(jì)算出CS的特征向量和特征值；

Step2：參照功能函數(shù)式F分別求出一階導(dǎo)數(shù)?g/?R和?g/?F；

Step3：將初始的迭代點(diǎn)設(shè)定為S(0)，一般情況下一般將均值點(diǎn)S-設(shè)立為初始迭代點(diǎn)，此時(shí)，β0=0；

Step4：在優(yōu)化迭代算法開始時(shí)，再形成剛度矩陣S-以及荷載列陣P-，解剛度方程得a-，形成驗(yàn)算點(diǎn)處的Ki，Pi，由式（1）求得ai；

Step5：通過計(jì)算建筑材料結(jié)構(gòu)控制面撓度σ求解變量結(jié)構(gòu)的隨機(jī)變量Si的一階偏導(dǎo)數(shù)，利用式（6）、（7）和（10）計(jì)算功能函數(shù)梯度的gradG(S)；

Step6：最后通過計(jì)算功能函數(shù)g(S)對(duì)迭代效果進(jìn)行算法收斂判斷，若g(S)≤ε，則對(duì)尋找的點(diǎn)可靠性指標(biāo)繼續(xù)進(jìn)行判別：如Δβ＞ε，則算法轉(zhuǎn)至Step3，繼續(xù)進(jìn)行迭代計(jì)算；若Δβ≤ε，則算法滿足收斂條件，停止迭代。

從上述的優(yōu)化迭代算法的基本步驟中看到，在Step4時(shí)，當(dāng)變異系數(shù)處于較低值的時(shí)候，能夠計(jì)算出驗(yàn)算點(diǎn)位移的大小。還可以計(jì)算出在均值處a，ai，aij位移發(fā)生后，再利用a*i=Si*-Si-的公式來求出位移a*。這種基于均值點(diǎn)的迭代算法記為RPSFEM2。

4 實(shí)驗(yàn)?zāi)M

在實(shí)驗(yàn)?zāi)M的部分將分三種情況來考慮設(shè)定的隨機(jī)參數(shù)的隨機(jī)性。首先是對(duì)彈性模量進(jìn)行的隨機(jī)性考察，在處理中將均布荷載當(dāng)作已經(jīng)確定的參數(shù)；再者需要對(duì)均布荷載的隨機(jī)性進(jìn)行考察；最后還需要將前兩者的情況同時(shí)考察。在這三種不同的建筑情況下，可以分別利用RPSFEM1和RPS?FEM2對(duì)建筑過程中的梁可靠度進(jìn)行分析，同時(shí)還需要將這些結(jié)果進(jìn)行比較并且做出誤差分析，分析如圖1～圖3所示。

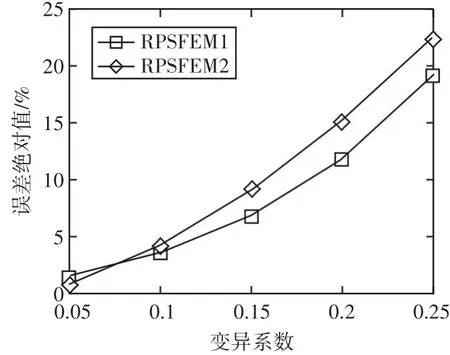
圖1建筑材料彈性模量隨機(jī)性

圖2建筑材料均布荷載隨機(jī)性

圖3建筑材料彈性模量和均布荷載隨機(jī)性

從圖1中不難發(fā)現(xiàn)，在彈性模量設(shè)定隨機(jī)的情況下，在變異系數(shù)低于0.10的情況下，采用RPS?FEM1以及RPSFEM2得出的演算結(jié)果未呈現(xiàn)出明顯的差異，同時(shí)通過RMCS的計(jì)算以及前者的計(jì)算均低于5%。在變異系數(shù)高于0.10時(shí)，與RPS?FEM1，RPSFEM2的計(jì)算方法相比，得出的結(jié)果與之前的計(jì)算方法得出的計(jì)算結(jié)果相對(duì)誤差較小。當(dāng)隨機(jī)系數(shù)開始變大的時(shí)候，RPSFEM1以及RPS?FEM2得出的演算結(jié)果的誤差也在相應(yīng)的增加，并且當(dāng)變異系數(shù)高于0.10時(shí)，兩者之間的誤差較大，而在變異系數(shù)為0.15時(shí)，誤差高達(dá)7%。

從圖2中不難發(fā)現(xiàn)，當(dāng)處于荷載隨機(jī)的狀態(tài)下，當(dāng)?shù)贸龅淖儺愊禂?shù)在逐步增加時(shí)，采用RPS?FEM1以及RPSFEM2得出的演算結(jié)果未呈現(xiàn)出明顯的差異。還發(fā)現(xiàn)，盡管采用RPSFEM1、RPSFEM2與RMCS方法得出的誤差和變異系數(shù)的增加呈現(xiàn)正相關(guān)，但是這樣的誤差并不超過1%。

從圖3中不難發(fā)現(xiàn)，在兩者同時(shí)隨機(jī)的情況下，當(dāng)?shù)贸龅淖儺愊禂?shù)在逐步增加時(shí)，采用RPS?FEM1以及RPSFEM2得出的演算結(jié)果未呈現(xiàn)出明顯的差異。但是與前者不同的在于，隨著變異系數(shù)的增大，它們的誤差也會(huì)增大。當(dāng)計(jì)算出的變異系數(shù)低于0.10時(shí)，采用前者計(jì)算方法得出的結(jié)果與后者得出的計(jì)算結(jié)果誤差小于5%。當(dāng)計(jì)算出的變異系數(shù)等于0.10時(shí)，采用前者計(jì)算方法得出的結(jié)果與后者得出的計(jì)算結(jié)果誤差都比較大。當(dāng)計(jì)算出的變異系數(shù)高于0.10時(shí)，采用前者計(jì)算方法得出的結(jié)果與后者得出的計(jì)算結(jié)果誤差高達(dá)6.6%。通過對(duì)比，能夠得出的結(jié)論是，在荷載隨機(jī)影響的情況下，利用RPSFEM1和RPSFEM2得出的計(jì)算結(jié)果是吻合得相對(duì)較好的。通過將第一種情況與第三種情況相對(duì)比我們也不能發(fā)現(xiàn)，在彈性模量的隨機(jī)影響下，當(dāng)變異系數(shù)高于0.15時(shí)，采用前者計(jì)算方法得出的結(jié)果與后者得出的計(jì)算結(jié)果誤差相對(duì)較高，高于5%，因此只能應(yīng)用于隨機(jī)參數(shù)較小的可靠度分析。

5 結(jié)語

本文以建筑結(jié)構(gòu)可靠性為出發(fā)點(diǎn)，重點(diǎn)分析了外荷載隨機(jī)性條件下的建筑材料彈性模量，旨在減少建筑用料。利用攝動(dòng)有限元算法結(jié)合隨機(jī)場效應(yīng)在計(jì)算可靠性指標(biāo)，構(gòu)建了蒙特卡洛有限元算法的結(jié)構(gòu)可靠性求解，分別利用Hasofer迭代和Or?thogonal變換優(yōu)化了算法的求解，并且通過建立基于驗(yàn)算點(diǎn)和均值點(diǎn)的迭代算法給出了節(jié)約條件下建筑用材的結(jié)構(gòu)可靠性。最后通過對(duì)建筑材料彈性模量的演算結(jié)果表明：利用細(xì)化后的兩種算法方式可為建筑節(jié)約用材條件下的可靠性進(jìn)行計(jì)算，這為減少建筑用材提供了數(shù)據(jù)計(jì)算保證。

［1］王鵬飛.淺談?dòng)?jì)算機(jī)輔助建筑設(shè)計(jì)與綠色建筑設(shè)計(jì)的結(jié)合［J］.計(jì)算機(jī)光盤軟件與應(yīng)用，2013（7）：40-41. WANG Pengfei.Discussion on the Combination of Comput?er Aided Architectural Design and Green Building Design［J］.Computer CD-ROM Software and Application，2013（7）：40-41.

［2］周春波.BIM技術(shù)在建筑施工中的應(yīng)用研究［J］.青島理工大學(xué)學(xué)報(bào)，2013，34（1）：51-54. ZHOU Chunbo.Application of BIM Technology in Build?ing Construction［J］.Journal of Qingdao Technological University，2013，34（1）：51-54.

［3］孫曉峰，魏力愷，季宏.從CAAD沿革看BIM與參數(shù)化設(shè)計(jì)［J］.建筑學(xué)報(bào)，2014（8）：41-45. SUN Xiaofeng，WEI Likai，JI Hong.Evolution of CAAD from BIM and Parametric Design［J］.Journal of Architec?tural Education，2014（8）：41-45.

［4］張瑞菊.SketchUp結(jié)合Google Earth在虛擬校園中的應(yīng)用［J］.計(jì)算機(jī)應(yīng)用，2013，33（1）：271-272. ZHANG Ruiju.The Application of SketchUp in Virtual Campus［J］.Computer Application，2013，33（1）：271-272.

［5］黃志煒，駱世廣，李綿升.動(dòng)態(tài)目標(biāo)的建筑供冷自適應(yīng)控制機(jī)制研究［J］.建筑節(jié)能，2013（5）：8-11. HUANG Zhiwei，LUO Shiguang，LI Jinsheng.Research on Adaptive Cooling Mechanism of Buildings with Dynamic Targets［J］.Building Energy Efficiency，2013（5）：8-11.

［6］諶文武，張宇翔，和法國.基于FLAC和遺傳算法的斜坡加固方案優(yōu)化方法［J］.中南大學(xué)學(xué)報(bào)（自然科學(xué)版），2011，42（11）：3507-3514. KAN Wenwu，ZHANG Yuxiang，HE Faguo.Optimization of Slope Reinforcement Schemes Based on FLAC and Ge?netic Algorithm［J］.Journal of Central South University（Natural Science），2011，42（11）：3507-3514.

［7］吳洲，葉倩，羅堃.基于粒子群算法的室內(nèi)環(huán)境節(jié)能優(yōu)化控制［J］.微計(jì)算機(jī)信息，2010，26（7）：159-161. WU Zhou，YE Qian，LUO Kan.Energy-saving optimiza?tion control of indoor environment based on particle swarm optimization［J］.Microcomputer information，2010，26（7）：159-161.

［8］張傳巖，洪曉光，彭朝暉.基于SVM和擴(kuò)展條件隨機(jī)場的Web實(shí)體活動(dòng)抽取［J］.軟件學(xué)報(bào)，2012，23（10）：2612-2627. ZHANG Chuanyan，HONG Xiaoguang，PENG Chaohui. Extraction of Web Entities Based on SVM and Extended Conditional Random Fields［J］.Journal of Software，2012，23（10）：2612-2627.

［9］丁光濤.變分法逆問題研究的若干進(jìn)展［J］.北京大學(xué)學(xué)報(bào)（自然科學(xué)版），2016，52（4）：732-740. DING Guangtao.Some Advances in Inverse Problem of Variational Method［J］.Journal of Peking University（Nat?ural Science），2016，52（4）：732-740.

［10］馮興中.工程結(jié)構(gòu)承載力極限狀態(tài)與正常使用極限狀態(tài)可靠度的比較分析［J］.西北水電，2011（2）：66-71. FENG Xingzhong.Comparison and Analysis of Bearing Capacity Limit State and Normal Service Limit State Reli?ability of Engineering Structures［J］.Northwest Hydro?power，2011（2）：66-71.

［11］劉國承，秦訓(xùn)鵬，魏青松.單軸壓縮金屬粉末材料屈服準(zhǔn)則研究［J］.華中科技大學(xué)學(xué)報(bào)（自然科學(xué)版），2016，44（7）：96-99. LIU Guocheng，QIN Xunpeng，WEI Qingsong.Study on Yield Criterion of Uniaxial Compression Metal Powder［J］.Journal of Huazhong University of Science and Tech?nology（Nature Science），2016，44（7）：96-99.

［12］楊綠峰，楊顯峰，余波.基于Nataf變換的層遞響應(yīng)面法分析結(jié)構(gòu)可靠度［J］.計(jì)算力學(xué)學(xué)報(bào)，2014（2）：155-160. YANG Lvfeng，YANG Xianfeng，YU Bo.Analysis of Structural Reliability by Layered Response Surface Meth?od Based on Nataf Transform［J］.Chinese Journal of Computational Mechanics，2014（2）：155-160.

［13］毛力奮.考慮可靠性和魯棒性的機(jī)械接頭有限元設(shè)計(jì)優(yōu)化［J］.計(jì)算機(jī)輔助工程，2010，19（3）：101-105. MAO Lifen.Optimization of Mechanical Joint Finite Ele?ment Design Considering Reliability and Robustness［J］. Computer Aided Engineering，2010，19（3）：101-105.

［14］練秋生，肖瑩.基于小波樹結(jié)構(gòu)和迭代收縮的圖像壓縮感知算法研究［J］.電子與信息學(xué)報(bào)，2011，33（4）：967-971. LIAN Qiusheng，XIAO Ying.Research on Image Com?pression Sensing Algorithm Based on Wavelet Tree Struc?ture and Iterative Shrinkage［J］.Electronics and Infor?matics，2011，33（4）：967-971.

［15］吳迪，王奎民，趙玉新.分段正則化正交匹配追蹤算法［J］.光學(xué)精密工程，2014，22（5）：1395-1402. WU Di，WANG Kuimin，ZHAO Yuxin.Piecewise Regu?larized Orthogonal Matching Pursuit［J］.Optics and Pre?cision Engineering，2014，22（5）：1395-1402.

Building Material Saving Based on Monte Carlo Finite Element Method

SHEN Lin1LI Xiaogang2
（1.Yangling Vocational&Technical College，Yangling712100）（2.Xi'anXiexinNewEnergyManagementCo.，Ltd，Xi'an733000）

In order to solve the problem of excessive consumption of building materials in real life，this paper takes the build?ing material saving material as the starting point，analyzes the structural load reliability index，and calculates the reliability index by the perturbation finite element method combined with the random field effect.The Monte Carlo finite element method for solving the problem of building material saving is constructed.By using the Hasofer iteration and the Orthogonal transformation，the func?tion function and the random variable transformation are optimized respectively.The point where the standard normal variable space and the central origin distance are minimum is taken as the core of the algorithm.The structural reliability of the building material is saved under the saving condition.The results show that the proposed algorithm is reliable in the case of small stochastic parameters and can be used as a reference for reducing the demand of building materials in the construction process.

finite element method，Monte Carlo method，building materials，structural reliability，material saving

TP391.7

10.3969/j.issn.1672-9722.2017.07.006

2017年1月7日，

2017年2月11日

申琳，女，碩士，講師，研究方向：建筑結(jié)構(gòu)。李曉剛，男，工程師，研究方向：工程管理。