可證安全的廣播多重盲簽名方案?

楊青 張惠玲 吳成晶

（西安航空學院理學院西安710077）

可證安全的廣播多重盲簽名方案?

楊青 張惠玲 吳成晶

（西安航空學院理學院西安710077）

對已有多重簽名方案進行了安全性分析，提出了可證安全的廣播多重盲簽名方案。給出了改進的廣播多重盲簽名算法和驗證算法，并證明了改進方案滿足盲性和不可偽造性。比較和分析了改進方案的復雜度和安全性，改進方案的運算量減少了37.2n+447.8TML。改進方案所需運算量少，安全性高且易于實現。

超橢圓曲線；約化除子；盲簽名；雙線性對

Class NumberTP309

1 引言

多個人合作對同一份消息進行簽名稱為多重數字簽名。Harn L在1989年提出了多重簽名方案，改進了RSA數字簽名方案［1］。在1994年，Harn L又提出了基于Meta-ElGamal方案的多重簽名方案［2］。根據簽名過程的不同，多重簽名可分為有序多重簽名和廣播多重簽名。有序多重簽名是指簽名者按照串行的順序進行簽名，廣播多重簽名對簽名順序沒有要求，簽名者可以同時進行簽名，不必遵循先后次序。2005年Harn L提出了基于RSA的有序和廣播多重簽名方案［3］。近年來，人們在超橢圓曲線上建立密碼系統［4］，并將雙線性對用于多重簽名方案［5～7］。

盲簽名是指簽名人在不知道消息內容的情況下對消息進行簽名。它在電子投票和銀行電子現金系統方面具有廣泛的應用［8］。盲簽名應滿足以下幾條性質：1）不可偽造性，任何第三方都不能偽造盲簽名；2）盲性，簽名人不知道所簽文件或消息的具體內容；3）不可追蹤性，簽名人無法將有效的簽名和被簽名的消息聯系起來。

本文對文獻［7］的多重簽名方案進行了改進，提出了高效的基于超橢圓曲線雙線性對的廣播多重盲簽名方案。首先提出改進的廣播多重盲簽名方案，給出簽名算法和驗證算法。其次，證明了算法的正確性和安全性。最后，比較和分析了改進方案的安全性和復雜度，并應用于超橢圓曲線密碼系統。改進算法克服了原方案不具有盲性的安全隱患，還保留了原方案的優點，并具有快速、高效且易于實現的特點。

2 雙線性映射

定義1設G1為循環加法群，G2為循環乘法群，G1，G2的階均為大素數q。設雙線性映射e:G1×G1→G2，它滿足以下三個性質：

1）雙線性：如果對于任意P，Q，R∈G1，a，b∈，e(P，Q+R)=e(P，Q) e(P，R)，e(P+Q，R)= e(P，R) e(Q，R)和e(aP，bQ)=e(abP，Q)=e(P，abQ)= e(P，Q)ab。

2）非退化性：存在P∈G1，使得e(P，P)≠1。

3）可計算性：若P，Q∈G1，則e(P，Q)可在多項式時間內有效計算。

3 改進的廣播多重盲簽名

該算法由n個簽名者A1，…，An，消息發送者I和簽名驗證者C組成。n個廣播簽名者A1，…，An可以同時進行簽名，不必遵循先后次序。

3.1 系統參數的設定

設G1，G2分別是階為q（q為大素數）加法群和乘法群。加法群G1的生成元為D，雙線性映射e:G1×G1→G2。H1和H2是兩個哈希函數：H1:{0，1}*×G1→Zq*，H2:{0，1}*→G1。系統公開參數Ω={G1，G2，H1，H2，e，q，D}。

3.2 簽名者密鑰的生成

n個簽名者A1，…，An的公鑰和私鑰生成：Ai隨機選取xi∈Zq*，計算公鑰Yi=xiD，私鑰為xi，(i=1，…，n)，若公鑰相同，則重新選取xi∈Zq*。

3.3 簽名的生成

對消息m產生一個廣播多重盲簽名，每個簽名者Ai(1≤i≤n)作如下運算：

1）簽名者Ai隨機選取ti∈Z*q，計算Ti=tiD，并將Ti發送給消息發送者I。

2）消息發送者I隨機選取αi，βi∈Zq*，首先計算αi-1∈Zq*，然后計算Ri=αiTi+βiYi+βiD，，h=H1(m，R)，h′i=αi-1h-αi-1βimodq， Q=H2(m∥R)，并將Q和h′i分別發送給簽名者Ai，將Q和h發送給簽名-驗證者C。-

3）簽名者Ai計算Wi=(ti-h′ixi)Q，并發送Wi給消息發送者I。-

4）消息發送者I驗證等式：e(D，Wi)= e(Ti-h′iYi，Q)是否成立。若不成立，則消息發送者I向簽名者Ai發出拒絕信息，或要求重新簽名。若成立，則I計算Wi=αiWi+βiQ，，則(R，W)為消息m的盲簽名，并發送(R，W)給簽名驗證者C。

3.4 簽名的驗證

3.5 正確性證明

證明：

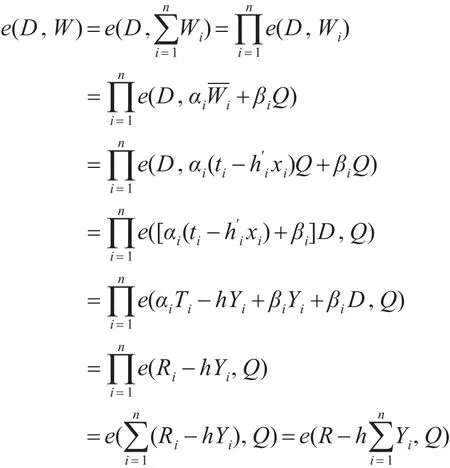
4 方案分析

4.1 安全性分析

1）盲性分析。改進方案具有盲性，即簽名人不能將消息與簽名聯系，從而判斷出消息和對應的盲簽名是否是他所簽。改進方案中，給定任意一個有效的廣播多重盲簽名(m，R，W)，，在盲簽名過程中產生的

i1， βi。總之，任何一個簽名者Ai都不能得出αi， βi。改進方案中任何一個簽名者Ai都不能將所簽消息和對應的盲簽名聯系起來，從而改進方案具有盲簽名的盲性。

2）方案具有不可偽造性。若攻擊者企圖冒充簽名者Ai的簽名-Wi=(ti-h′ixi)Q，需求解xi。這必需求解超橢圓曲線離散對數問題，在計算上是不可行的。若攻擊者企圖偽造消息m的盲簽名(R，W)，由于攻擊者無法得到αi，βi（見盲性分析），就不能計算出。所以，方案具有不可偽造性。

3）防止簽名集體內部人員偽造盲簽名。若簽名集體內部的某個簽名者想偽造Ai的簽名，那他必須通過消息發送者I的驗證。假設他可以獲得αi，βi，但需要計算-Wi=(ti-h′ixi)Q，這需要求解xi，等同于求解超橢圓曲線離散對數問題，這在計算上是不可行的。所以改進方案能夠防止簽名集體內部人員偽造盲簽名。

4.2 效率分析

本文的方案與文獻［9］進行了效率比較，不同密碼體制下的運算量轉換關系（表1），選取虧格為2的超橢圓曲線，且特征為2。高效的超橢圓曲線除子加法和倍點運算的計算公式，參見文獻［10～11］。除子加法運算的運算量為1I+3S+22M，并且除子倍點運算的運算量為1I+5S+22M，其中I，S，M分別表示有限域上的求逆、平方和乘法，并有1I= 30M，1S=0.8M。假定簽名者人數均為n，改進方案總的計算量為(n+1)TBP+(8n+1)THEM+(7n-2)THEA，由表1中可得，轉換后運算量為(922.8n+32.2)TML。文獻［9］方案的總計算量為(4n+2)TEX，即轉換后運算量為(960n+480)TML。因此，本文的運算時間量減少了(37.2n+447.8)TML，改進方案具有運算量少，效率高等優點。

表1 不同密碼體制下的操作運算轉換關系

5 結語

本文提出了基于超橢圓曲線雙線性對的廣播多重盲簽名方案，廣泛應用于匿名電子投票系統，電子現金交易、網絡職稱評審及電子銀行系統等。比較和分析了改進方案的安全性和效率，與文獻［9］的計算效率相比較，改進方案的運算量減少了(37.2n+447.8)TML。改進方案具有運算量低，高安全性能以及易于實現等優點。

［1］Harn L，Kiesler T.New schem for digital multisignatures［J］.Electronics letters，1989，25（15）：1002-1003.

［2］Harn L.New digital signature scheme based on discrete logarithm［J］.Electronics letters，1994，30（5）：396-398.

［3］Harn L，Lin CY，Wu C T.Structured multisignature algo?rithms［J］.IEE computers and digital techniques，2004，151（3）：231-234.

［4］Yang Siman，Wu Hongfeng，LI Jiyou.Access structures of hyperelliptic secret sharing schemes［J］.Finite Fields and Their Applications，2016，37（1）：46-53.

［5］Islam S.H.，Biswas G.P.A provably secure identity-based strong designated verifier proxy signature scheme from bi?linear pairings［J］.Journal of King Saud University--Com?puter and Information Sciences，2014，26（1）：55-67.

［6］Islam S.H.，Biswas G.P.Provably secure certificateless strong designated verifier signature scheme based on ellip?tic curve bilinearpairings［J］.Journal of King Saud Univer?sity--Computer and Information Sciences，2013，25（1）：51-61.

［7］Islam S.H.，Biswas G.P.Certificateless short sequential and broadcast multisignature schemes using elliptic curve bilinear pairings［J］.Journal of King Saud Universi?ty--Computer and Information Sciences，2014，26（1）：89-97.

［8］Li Fagen，Zhang Mingwu，Takagi Tsuyoshi.Identity-based partially blind signature in the standard model for electron?ic cash［J］.Mathematical and computer modeling，2013，58（1）：196-203.

［9］Debasis Giri，Srivastava P.D..An improved efficient mul?tisignature scheme in group communication systems［C］// Proceedings of the 2007 International Conference on Ad?vanced Computing and Communications（ICACC'07），2007：447-435.

［10］李明，孔凡玉，朱大銘.超橢圓曲線上Montgomery標量乘的快速計算公式［J］.軟件學報，2013，24（10）：2275-2288. LI Ming，KONG Fanyu，ZHU Daming.Fast addition for?mulae for Montgomery Ladder scalar multiplication on hyperelliptic curves［J］.Journal of Software，2013，24（10）：2275-2288.

［11］Lange T.Formulae for arithmetic on genus 2 hyperellip?tic curves［J］.Applicable algebra in engineering，com?munication and computing，2005，15（5）：295-328.

Provably Secure Broadcast Blind Multisignature Scheme

YANG QingZHANG HuilingWU Chengjing
（Faculty of Science，Xi'an Aeronautical University，Xi'an710077）

Multisignature algorithm by reference is analyzed.Provably secure broadcast blind multisignature scheme is pre?sented.Specific signature and verification algorithms of Improved broadcast blind multisignature scheme are given.And the Im?proved scheme meets the properties of both blindness and non-forgery.The complexity and security of improved scheme are com?pared and analyzed.Improved scheme reduces computation costs 37.2n+447.8TML.Improved scheme has the advantages of low com?putation complexity，high security and easy to achieve.

hyperelliptic curve，reduced divisors，blind signature，bilinear pairings

TP309

10.3969/j.issn.1672-9722.2017.07.026

2017年1月10日，

2017年2月27日

國家自然科學基金（編號：11302158；11626182）；陜西省科技廳項目（編號：2013JM1019；2014K05-43）；陜西省教育廳項目（編號：14JK1310）；西安航空學院基金項目（編號：2015KY1218；2016GJ1004）資助。

楊青，女，碩士，講師，研究方向：密碼學。張惠玲，女，博士，副教授，研究方向：科技評價、信息安全。吳成晶，女，碩士，助教，研究方向：數論和密碼學。