錯距旋壓工藝參數對輪轂輪輞成形影響規律探究

文／李萍，劉國凱，吳信濤，謝瑞，杜勇，薛克敏·合肥工業大學

錯距旋壓工藝參數對輪轂輪輞成形影響規律探究

文／李萍，劉國凱，吳信濤，謝瑞，杜勇，薛克敏·合肥工業大學

為系統地研究汽車輪轂強力旋壓成形規律，在對輪轂強力旋壓工藝分析的基礎上，建立符合實際的力學模型。利用有限元分析軟件對輪轂的錯距旋壓過程進行數值模擬，得到旋壓成形過程中的應力應變分布情況，分析變形區金屬流動規律和塑性成形機理，并對軸向錯距量、徑向壓下量等重要工藝參數進行優化分析，找出最優工藝參數。

輪轂是車輛行駛時的主要部件之一，發揮著承載車輛重量、體現車輛外觀、轉向和驅動等重要作用。旋壓是一種綜合了鍛造、擠壓、拉深、彎曲和滾壓等工藝特點的先進制造工藝方法，在航空航天、通用機械、汽車和化工等金屬精密加工技術領域得到了日益廣泛的應用。作為一種先進的制造技術，旋壓也開始逐漸應用到汽車輪轂的制造和生產中去。

國外生產鋁合金輪轂已經開始廣泛采用強力旋壓和普通旋壓復合的生產工藝，但其需兩臺旋壓機床，兩道次工序增加了影響零件質量的因素，使其精度更難控制。錯距旋壓采用三旋輪錯距分布同時對工件進行加工，可以將需要多道次完成的工序在一道次中完成，生產效率得到了大幅度提高，且工件質量更容易控制。

有限元模型建立

圖1(a）為輪轂鑄坯，輪輞部分壁厚為10mm，圖1(b）為最終零件，輪輞壁厚為5mm，輪輞厚度減薄率達到了50%。采用一道次普通旋壓成形工藝，輪輞復雜曲母線勢必為成形難點，且零件的精度和成形質量難以得到保證。采用錯距旋壓工藝，可大大降低每道次坯料減薄率，避免材料在變形過程發生拉裂、過度減薄等問題，且零件表面質量良好。本文輪轂材料選用A356，所用工藝參數如表1所示。

圖1 輪轂模型

輪轂錯距旋壓成形模擬結果與分析

錯距旋壓應力分析

如圖2(a）、(b）所示，在錯距旋壓初期，隨著旋輪在軸向的進給運動和徑向的往復運動，坯料受到等效應力逐漸增大，隨后呈現減小趨勢。外表面的等效應力呈環形分布于變形區，此時，等效應力最大值分布于旋輪作用區，這是因為在旋壓初期，已變形區域相對未變形區域還比較小，旋壓過程中已變形區受到未變形區凸緣“剛端”的影響，將更大的偏離正弦律，造成附加的徑向拉應力和周向壓應力。在旋壓成形的后期，如圖2(c）、(d）所示，已變形區比未變形區要大，所受到凸緣“剛端”的影響變小，偏離正弦律變小，因此等效應力的分布區域相對減小，內表面等效應力分布規律與外表面的規律相同。內外表面等效應力的最大值始終出現在旋輪的作用區域范圍。

表1 模擬實驗方案

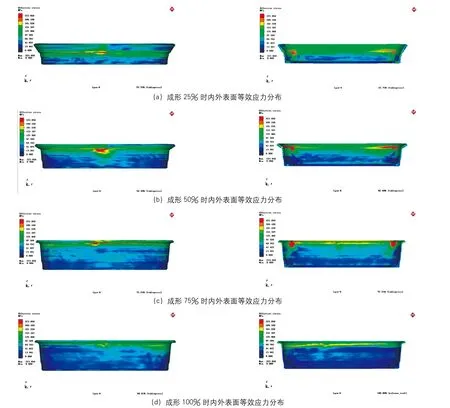
圖2 成形過程中內外表面的等效應力分布

錯距旋壓應變分析

如圖3所示，在旋壓變形過程中，外表面的等效塑性應變在變形初期呈現增大的趨勢，隨后隨著變形的進行逐漸減小，由圖可見，在坯料的中間部位出現了一個塑性應變極大值集中區——應變環，且應變分布比較均勻。

應變環產生與材料減薄率有關，主要由以下兩方面原因造成：

⑴旋壓成形初、中期，已變形區相比凸緣“剛端”較小，變形區受到凸緣“剛端”的影響較大，坯料的內錐角會相對增大，如圖3(a）、(b）所示，壁厚減薄率與坯料內錐角正相關，此時旋壓件的壁厚減薄率亦增大；在旋壓成形中后期，變形區受到凸緣的影響逐漸減小，內錐角變化將隨之減小，如圖3(c）、(d）所示，旋壓成形逐漸恢復正常，實際的減薄率也相應減小。

圖3 成形過程中內外表面的等效塑性應變分布

⑵旋壓變形中以剪切變形為主，變形金屬向旋輪后方流動，但在金屬流動阻力的作用下，少量變形區金屬將流向旋輪前方，在旋輪前方產生隆起。變形初期，已變形區相比凸緣“剛端”較小，變形區受到凸緣“剛端”的影響較大，形成的隆起較高，如圖3(a）、(b）所示，坯料隆起使得工件變形區的坯料厚度增大，厚度減薄率增大，即旋壓變形程度增大，等效塑性應變相應增大。隨著旋壓變形的進行，變形區受凸緣“剛端”的影響逐漸減小，旋輪前方形成的隆起逐漸減少，如圖3(c）、(d）所示，金屬堆積減小，使得等效塑性應變相應減小。

錯距值對輪轂旋壓成形的影響

⑴軸向錯距量對旋壓力的影響。

軸向錯距值的合理分配，在保證金屬的正常流動時，還需保證各個旋輪的受力均勻。圖4為旋輪間錯距值與各個旋輪軸向、徑向、切向旋壓力之間的關系。由圖4(a）、(b）、(c）可知，在三個方向上的旋壓力均在錯距值為2mm時取的最小值。在三個方向上旋壓力的變化趨勢相同，當錯距值由1mm增大到2mm時，三個方向上的旋壓力均由大變小；而后當錯距值由2mm增大到3mm時，三個方向上的旋壓力均由小變大。且三個方向上的旋壓力分配均為：1號旋輪＞2號旋輪＞3號旋輪，可見各個旋輪的負荷較為均勻。因此在鋁合金輪轂錯距旋壓數值模擬時，錯距值選擇為2mm較為合理，有助于降低旋壓力。

⑵軸向錯距量對等效應力的影響。

軸向錯距量對等效應力的影響如圖5所示。由等效應力云圖可以看出，當軸向錯距量為2mm時，等效應力分布區域相對較小，且較為均勻。軸向錯距量為1mm和3mm時，等效應力分布區域相對較大且不均勻，易導致坯料變形失穩。

各旋輪下壓量對旋壓成形的影響

⑴徑向壓下量對旋壓力的影響。

各旋輪壓下量的不同分配勢必引起旋壓力的不同。表2中第一組壓下量采用等量分配法，Δt1=Δt2=Δt3=1.67mm，錯距旋壓過程中三旋輪的徑向力F1＞F2＞F3，這是由于坯料經前一個旋輪成形后造成坯料加工硬化，坯料的強度得到一定提高，后道次旋壓力增加。此外在第一組壓下量的分配下，旋輪徑向力的均方差為三組中最大，各旋輪之間的徑向力分配不平衡導致成形時工件的變形不均勻。

圖4 旋輪間錯距值對三旋輪旋壓力的影響

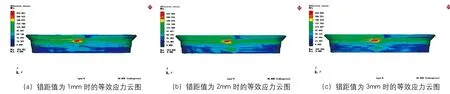
圖5 旋輪間錯距值對等效應力的影響

第二組壓下量分配為Δt1＞Δt2=Δt3，因為1#旋輪的壓下量明顯大于2#、3#旋輪的壓下量，所以1#旋輪所受的徑向力最大；2#旋輪和3#旋輪的壓下量相同，但2#旋輪的徑向力要比3#旋輪的徑向力略大，這與第一組的原因相同；但在第二組壓下量分配下，各旋輪徑向力的均方差為三組中最小，各旋輪之間的徑向力分配相對平衡，有利于坯料的均勻變形。

表2 不同壓下量對徑向旋壓力的影響

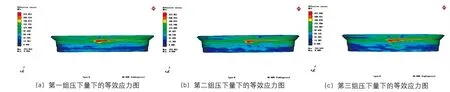
圖6 壓下量對等效應力的影響圖

第三組壓下量分配為Δt1＞Δt2＞Δt3，三旋輪的徑向力F1＞F2＞F3，徑向力的均方差略大，各旋輪之間的徑向力分配相對不平衡。

⑵徑向壓下量對等效應力的影響。

圖6為不同壓下量2#旋輪變形區的等效應力狀態。2#旋輪作為中間旋輪，其作用區的應力狀態能夠較好的反映整個坯料的變形情況。圖6(b）和(c）的紅色區域分布較為相似，且明顯比圖(a）中的區域分布要小，等效應力狀態更加均勻，坯料變形亦更為均勻；而圖(b）中的紅色區域相對于圖(c）更均勻一點，即變形更均勻。這與在徑向旋壓力對比中得到的結論相同。

試驗驗證

選用錯距量為2mm，壓下量選擇第二組的工藝參數下進行試驗驗證，將A356鑄坯輪輞進行錯距旋壓成形，得到工件如圖7所示，輪輞在成形過程中無折疊、起皺，表面質量良好。

圖7 輪轂錯距旋壓實物圖

結論

⑴在錯距旋壓過程中，應力值由坯料的外表面向內表面逐漸減小；等效應力隨著變形程度的增加而增大，而等效應變的分布則經歷了先增大后減小的過程。

⑵旋輪作用區受到三向壓應力作用，由于在三個方向上受力的不同，迫使變形坯料在軸向上以伸長變形為主，徑向上坯料以發生壓縮變形為主。作用區的下方區域，坯料在軸向處于伸長變形，作用區的上方區域，坯料在徑向上發生伸長變形，軸向上發生壓縮變形。

⑶旋壓力隨著錯距值的增大先變小后增大，在錯距值為2mm時旋壓力最小；徑向壓下力在徑向壓下量為2mm、1.5mm、1.5mm時均方差最小，此時坯料變形均勻，變形區等效應力亦在此組壓下量作用下最為均勻。