偏心布筋曲梁振動微分方程推導和求解

何文正, 陳 晨, 李鵬程, 文競舟

(1. 重慶廣播電視大學 城市建設工程學院，重慶 400052；2. 宜賓職業技術學院 建筑工程系，四川 宜賓 644000；3. 重慶交通科研設計院 道路所，重慶 400067；4. 云南省公路科學技術研究院 巖土所，云南 昆明 650051)

?

偏心布筋曲梁振動微分方程推導和求解

何文正1, 陳 晨2, 李鵬程3, 文競舟4

(1. 重慶廣播電視大學 城市建設工程學院，重慶 400052；2. 宜賓職業技術學院 建筑工程系，四川 宜賓 644000；3. 重慶交通科研設計院 道路所，重慶 400067；4. 云南省公路科學技術研究院 巖土所，云南 昆明 650051)

為研究預應力筋偏心距和半徑等參數對曲梁振動特性的影響，以自由振動狀態下的曲梁微段為研究對象，考慮偏心布筋產生的初始曲率對振動的影響，推導了偏心布筋曲梁振動偏微分方程，并求解方程得到了簡支曲梁面內振動1階頻率理論計算公式；最后通過實例分析驗證了所提理論公式的正確性。

橋梁工程；曲梁；偏心布筋；初始曲率；自振頻率

預應力曲梁在工程中已經得到廣泛的應用，其動力特性是曲梁設計所關注的重要內容，良好的動力特性是滿足曲線梁橋抗震、抗風性能的前提，也是保證結構安全營運的關鍵[1-2]。

目前，國內外已有不少學者對曲梁的動力特性進行了理論研究。C．H．KOU等[3]提出了薄壁曲梁的有限梁段法進行了曲梁自振頻率的分析；單德山[4]應用積分變換法求解了移動荷載作用下的曲梁振動方程，并研究了曲梁彎扭耦合振動機理和薄壁曲線箱梁的振動特性；Y．B．YANG等[5]對曲梁強迫振動進行了研究；葉康生等[6]則采用動力剛度法求解了曲梁面外振動問題；宋郁民等[7-8]采用數學物理方法推導了曲梁振動微分方程組，求解得到了半解析表達式。但是，曲梁的試驗研究較少，動力特性試驗研究數據相對缺乏。

在以往的曲梁動力特性研究中，基本沒有考慮預應力的作用，也未研究力筋布置方式對曲梁動力特性的影響，而目前工程中使用的曲梁基本上為偏心布筋預應力曲梁，其動力特性的計算基本上采用有限單元法進行[9-10]，雖然有限元法功能強大，幾乎能夠求解所有數學模型的初值問題，但采用解析法更能深入研究曲梁振動內在規律。

筆者采用達朗貝爾原理推導了偏心布筋曲梁振動微分方程，并考慮了預應力以及偏心布筋產生的初始曲率對振動特性的影響。提出了偏心布筋曲梁一階面內自振頻率計算公式，并通過實例分析驗證了該公式。

1 偏心布筋曲梁振動微分方程

1.1 推導假定

在進行偏心布筋曲梁振動微分方程的推導前，筆者做了以下基本假定：①曲梁為等截面勻質圓弧曲梁，半徑為常數R；②預應力筋直線偏心布置，其預應力大小為P，橫向和豎向偏心距為e1和e2；③曲率半徑遠大于橫截面尺寸，忽略梁曲率影響。

采用三維流動直角坐標系，坐標系符合右手螺旋法則規定，正方向規定如圖1。

圖1 三維流動坐標系Fig. 1 Three-dimensional flow coordinate system

1.2 力筋偏心布置產生的初始彎矩

在曲線預應力筋的預加力P作用下，在L(切向)、M(徑向)、N(豎向)產生3個外荷載[11]，如圖2。

圖2 截面內的預應力和內力Fig. 2 Prestress and internal force in section

1.3 建立振動微分方程

對于預應力筋偏心布置的無黏結預應力混凝土梁，在自由振動時，取出梁上的一段微元體進行受力分析，微元體內力如圖3。

圖3 曲梁微段截面內力Fig. 3 Internal force of the micro segment of the curved beam

利用彎曲梁段的6個空間平衡條件，考慮軸向力與梁曲率的乘積在力矩平衡方程中形成的附加項，根據達朗貝爾原理得出6個平衡方程：

(1)

(2)

(3)

(4)

(5)

(6)

式中：m為曲梁單位長度質量；N為軸向內力；T為扭矩；Mx為豎向彎矩；My為橫向彎矩；ρ為曲梁密度；u，v，w分別為縱向、徑向和豎向位移；φ為扭角。

化簡可得到以下4個基本方程：

(7)

(8)

(9)

(10)

代入幾何、物理方程可建立曲梁內力與變形之間的關系[12]，將幾何、物理方程代入式(7)～(10)中可得

(11)

(12)

(13)

(14)

式中：A為曲梁截面面積；Ix為繞x軸的抗彎慣矩；E為梁的彈模；Iy為繞y軸的抗彎慣矩；G為剪切模量；Id為抗扭慣矩；Iw為梁的扇性慣矩。

分析式(11)～(14)可知，此時方程組中并不包含力筋的橫向和豎向坐標e1和e2；但需要注意到當預應力筋偏心布置時，預應力會對曲梁產生橫向和豎向附加彎矩，從而使梁體產生初始撓度。而此時梁體是以該初始撓度為平衡位置進行自由振動，因此，梁上各點的振動位移為附加彎矩產生初始位移以及自由振動產生的位移增量之和[13]，即

(15)

(16)

(17)

式中：腳標Δ表示振動產生的位移增量。

預應力產生的初始位移可用靜力學方法得到，將式(15)～(17)對z和t求導，并代入式(11)～(14)可得到考慮偏心布筋的曲梁振動方程組：

(18)

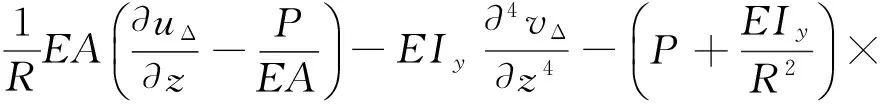
(19)

(20)

(21)

式(18)～(21)即為偏心布筋曲梁振動微分方程。令：e1=e2=0，P=0；則式(18)～(21)退化為宋郁民等[7]所提出的方程，即不考慮預應力效應的曲梁振動微分方程。

當e1=e2=0、曲梁半徑R→∞，式(18)～(21)則退化為考慮軸力影響的直梁振動方程[14]。

2 方程求解

2.1 邊界條件

筆者考慮單跨超靜定簡支曲梁的情況，如圖4。

其邊界條件為：

u(0)=0，u′(l)=0

(22)

v(0)=v(l)=0，v″(0)=v″(l)=0

(23)

w(0)=w(l)=0，w″(0)=w″(l)=0

(24)

φ(0)=φ(l)=0，φ′(0)=φ′(l)=0

(25)

圖4 單跨曲梁支承布置Fig. 4 Support arrangement of a single span curved beam

2.2 微分方程求解

考察微分方程式(18)和式(19)，方程中徑向振動和縱向振動相互耦合，由于橋梁結構軸向拉壓剛度極大，軸向變形很小，可忽略軸向變形，在忽略曲梁縱向振動的情況下面內振動方程可以解耦，從而實現方程的求解。但面外振動由于彎扭耦合的影響，求解方法還需要進一步研究。

僅考慮曲梁面內的振動，在忽略軸向變形的情況下有

(26)

將式(15)和式(16)代入式(26)，再將所得方程式代入式(19)，可得：

(27)

在預應力筋偏心布置的情況下，梁體振動時預應力大小也為一個變化量，可通過平截面假定推導出振動中的預應力值為[13]：

(28)

式中：P0為預應力筋的初始張拉力；Et，At分別為鋼束的彈性模量和鋼束面積。

將式(28)代入式(27)，并化簡得到：

(29)

式(29)為非齊次非線性偏微分方程，可采用Galerkin法求得近似解。

選取形狀函數φr(x)和權函數qr(t)，構造橫向振動位移函數：

(30)

將式(30)代入式(29)，并對得到的算式在區間(0≤x≤l)上進行加權積分，取簡支梁1階振型函數φ1(x)=sin(πx/l)作為形狀函數和權函數代入算式，簡化得到：

(31)

對式(31)進行積分得：

(32)

式(32)為一個單自由度自治系統，仍用Galerkin法求解體系自振頻率，構造方程的近似解為：

q(t)=acos(ωt)

(33)

式中：ω=2π/T，a為振幅，T為周期。

將q(t)代入式(32)得到殘差力：

(34)

(35)

式(35)為偏心布筋曲梁面內振動1階自振頻率近似計算公式。令偏心距e1=0且曲梁半徑R趨于無限大，則式(35)就退化為軸心布筋直線梁1階自振頻率公式[14]：

(36)

通過對式(35)的分析，可知：①偏心布筋曲梁1階面內振動頻率除了與自身的質量和剛度分布有關以外，還與曲線半徑、軸力大小以及偏心距有關，當R趨于無限大時且偏心距為0時，曲梁的頻率則退化為直梁的頻率；②偏心直線布筋會對曲梁自振頻率產生影響，偏心距越大，自振頻率越大。

3 數值驗證

3.1 建立有限元分析模型

采用有限元程序驗證所提的近似計算公式的正確性。算例采用矩形截面實心梁；梁高h=1.6 m，寬b=0.8 m，l=30 m，偏心直線布筋，曲梁半徑分別取60、100、200、500、10 000 m；混凝土彈性模量E=3.5×1010N/m2，混凝土密度ρ=2 500 kg/m3，預應力筋彈性模量Et=2.1×1011N/m2，面積At=2.8×10-3m3，密度ρ=7 800 kg/m3；預應力采用降溫法進行模擬，力筋分別按照偏心距e分別取0、0.2、0.3 m布置。分別采用有限元程序和式(35)計算預應力大小為P0分別取0、10、20 kN時的曲梁面內1階自振頻率。二者計算結果比較如表1～表3和圖5。

表1 自振頻率計算結果對比(P0=0 kN)

表2 自振頻率計算結果對比(P0=10 kN)

表3 自振頻率計算結果對比(P0=20 kN)

圖5 不同偏心距(P0=0 kN)和預應力(e=0.3 m)下的1階頻率Fig. 5 First order frequency with different eccentricities (P0=0 kN) and prestress values (e=0.3 m)

3.2 計算結果及相關參數的影響分析

按照式(35)計算的偏心布筋曲梁面內自振頻率與有限元計算結果較為吻合，最大的誤差為3.38%；自振頻率隨著預應力值增大而減小，公式計算和數值計算結果都表明預應力值對頻率的影響極小。

在偏心布筋情況下，曲梁自振頻率隨著半徑的增加而逐漸降低。在半徑小于200 m時，曲梁半徑對頻率影響較明顯；當半徑過200 m時，對頻率的影響較小。

曲梁的1階面內自振頻率隨偏心距的增加而增大，與有限元分析結果吻合，其直梁頻率變化趨勢與李榮[15]所得出的結論一致，相對于預應力值和半徑來說，偏心距對頻率的影響更為明顯。

根據對比分析結果可知，采用筆者所提出的計算公式能較好地進行偏心布筋曲梁的1階面內振動頻率計算，公式能較好的地反映曲梁的頻率隨偏心距、半徑及預加力大小變化的趨勢。

4 結 論

筆者推導了偏心布筋曲梁的自由振動微分方程組；并求解面內振動方程得出了曲梁面內振動1階頻率近似計算公式；分析了偏心距、預加力和半徑等參數對自振頻率的影響；數值分析結果與理論公式計算結果吻合，證明了方程的推導及求解的正確性。

結果表明：①預應力值對曲梁動力特性影響極小，計算中可以不考慮；②曲梁半徑對動力特性影響較預應力值明顯，但是當半徑大于200時，曲梁半徑對動力特性影響較小；③偏心距對頻率的影響較明顯，計算中不宜忽略。

[1] 趙躍宇，康厚軍，馮銳，等．曲線梁研究進展[J]．力學進展，2006，36(2)：170-186． ZHAO Yueyu, KANG Houjun, FENG Rui, et al. Advances of research on curved beams[J].AdvancesinMechanics, 2006, 36(2): 170-186.

[2] 謝秉敏，向中富，王小松，等．基于ANSYS的車橋耦合動力分析[J]．重慶交通大學學報(自然科學版)，2012，31(5)：935-938． XIE Bingmin, XIANG Zhongfu, WANG Xiaosong, et al. Dynamic analysis method of vehicle-bridge coupling based on ANSYS[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2012, 31(5): 935-938.

[3] KOU C H, BENZLEY S E, HUANG J Y, et al. Free vibration analysis of curved thin-walled girder bridges[J].JournalofStructuralEngineering, 1992, 118(10): 2890-2910.

[4] 單德山．高速鐵路曲線梁橋車橋耦合振動分析及大跨度曲線梁橋設計研究[D]．成都：西南交通大學，1999：14-46． SHAN Deshan.Curved-GirderBridgesandVehiclesCoupledVibrationAnalysisandDesignStudyoftheLong-SpanCurved-GirderBridgesinHigh-SpeedRailway[D]. Chengdu: Southwest Jiaotong University, 1999:14-46.

[5] YANG Y B, WU C M, YAU J D. Dynamic response of a horizontally curved beam subjected to vertical and horizontal moving loads[J].JournalofSoundandVibration,2001,242(3):519-537.

[6] 葉康生，趙雪健．動力剛度法求解平面曲梁面外自由振動問題[J]．工程力學，2012，29(3)：1-8． YE Kangsheng, ZHAO Xuejian. Dynamic stiffness method for out-of-plane free vibration analysis of planar curved beams[J].EngineeringMechanics, 2012, 29(3):1-8.

[7] 宋郁民，吳定俊，李奇．圓弧曲梁振動微分方程推導及振動特性分析[J]．沈陽建筑大學學報(自然科學版)，2012，28(3)：400-404． SONG Yumin, WU Dingjun, LI Qi. Derivation of vibration differential equation and analysis of vibration properties about ARC-curved beam [J].JournalofShenyangJianzhuUniversity(NaturalScience), 2012, 28(3): 400-404.

[8] 宋郁民．曲梁振動微分方程組求解[C]//中國力學學會《工程力學》編委會．第23屆全國結構工程學術會議論文集：第Ⅰ冊．2014：258-264． SONG Yumin. Solving the differential equations of curved beams [C]//Editorial Board of Engineering Mechanics, Chinese Society of Mechanics.Proceedingsofthe23rdNationalConferenceonStructuralEngineering:VolumeI. 2014:258-264.

[9] 馮東明，李愛群，李建慧，等．獨塔斜拉與連續剛構組合橋梁動力特性及參數影響分析[J]．重慶交通大學學報(自然科學版)，2010，29(3)：329-332． FENG Dongming, LI Aiqun, LI Jianhui, et al. Research on dynamic behavior and parameter influence of single pylon cable-stayed and continuous rigid-frame composite bridge[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2010, 29(3): 329-332.

[10] 梁甜甜，向中富，卞明智，等．曲梁預應力摩阻損失試驗研究[J]．重慶交通大學學報(自然科學版)，2008，27(增刊)：871-874． LIANG Tiantian, XIANG Zhongfu, BIAN Mingzhi, et al. Test and study of attrition loss of pre-stressed wire of curved box girder[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2008, 27(Sup): 871-874.

[11] 邵容光，夏淦．混凝土彎梁橋[M]．北京：人民交通出版社，1996：212-216． SHAO Rongguang, XIA Gan.ConcreteCurvedGirderBridge[M]. Beijing: China Communication Press, 1996: 212-216.

[12] 姚玲森．曲線梁[M]．北京：人民交通出版社，1989：1-14． YAO Lingsen.CurvedBeam[M]. Beijing: China Communications Press, 1989:1-14.

[13] 王龍林．簡支梁自振頻率的預應力效應分析[D]．長春：吉林大學，2013: 53-77． WANG Longlin.AnalysisofPrestressingEffectonNaturalFrequencyforSimplySupportedBeam[D]. Changchun: Jilin University, 2013: 53-77.

[14] 劉晶波，杜修力．結構動力學[M]．北京：機械工業出版社，2005：160-169． LIU Jingbo, DU Xiuli.StructuralDynamics[M]. Beijing: China Machine Press, 2005: 160-169.

[15] 李榮．無粘結預應力混凝土梁動力特性研究[D]．包頭：內蒙古科技大學，2013：7-33． LI Rong.StudyonDynamicPeculiarityforUnbondedPre-stressedConcreteBeam[D]. Baotou: Inner Mongolia University of Science and Technology, 2013:7-33.

(責任編輯：劉 韜)

Derivation and Solution of Vibration Differential Equation of theCurved Beam with Eccentric Reinforce

HE Wenzheng1, CHEN Chen2, LI Pengcheng3, WEN Jingzhou4

(1. School of Urban Construction Engineering, Chongqing Radio & TV University, Chongqing 400052, P. R. China;2. Department of Architecture Engineering, Yibin Vocational and Technical College, Yibin 644000, Sichuan, P. R. China; 3. Road Research Institute, Chongqing Communications Research and Design Institute, Chongqing 400067, P. R. China;4. Rock and Soil Engineering Institute, Yunnan Science & Technology Research Institute of Highway, Kunming 650051, Yunnan, P. R. China)

In order to study the influence of tendon eccentricity and radius on the vibration characteristics of the curved beam, the differential equation of the vibration of the prestressed curved beam considering the influence of initial curvature on vibration was derived by analyzing the micro section of the curved beam under the condition of free vibration. Then the theoretic calculation formula of the first order natural frequency vibration of the eccentric reinforcement simply supported curved beam was deduced by solving the equation. Finally, the correctness of the proposed theoretic formula was verified by the case study.

bridge engineering; curved beam; eccentric reinforce; initial curvature; natural frequency of vibration

10.3969/j.issn.1674-0696.2017.07.03

2015-12-02；

2016-07-16

交通運輸部建設科技項目(2013318791440)；重慶廣播電視大學重點基金項目(ZD2015-02)

何文正(1982—)，男，重慶人，講師，碩士，主要從事橋梁檢測加固方面的研究。E-mail：hewenzheng1982@126.com。

U441.2

A

1674-0696(2017)07-015-06