黃土隧洞變形及穩定性分析

馮 興，姚仰平，霍海峰

(1. 中國民航大學 機場學院，天津 300300；2. 北京航空航天大學 交通科學與工程學院，北京 100191)

?

黃土隧洞變形及穩定性分析

馮 興1，姚仰平2，霍海峰1

(1. 中國民航大學 機場學院，天津 300300；2. 北京航空航天大學 交通科學與工程學院，北京 100191)

以黃土隧洞的應力變形及穩定性分析為研究目標，首先基于考慮黏聚力c值的SMP準則，對原UH模型進行改進，建立了考慮c值的UH模型，使得UH模型能夠用于隧洞開挖等問題的分析；然后應用半隱式回映算法對應力進行更新，采用Newton-Raphson算法進行非線性問題的解答，編制了考慮c值UH模型的有限元程序，并將初始超固結比OCR作為參數引入到有限元程序中；進而對一無襯砌黃土隧洞進行了三維有限元分析，比較分析了應用原UH模型、考慮c值的UH模型和Mohr-Coulomb模型計算得到隧洞周圍土體的位移。說明了應用考慮c值的UH模型進行隧洞計算分析的合理性，得出了隧洞周圍土體的位移變化規律，并應用考慮c值的UH模型研究了隧洞周圍土體的應力應變規律，而且應用有限元強度折減法，對隧洞的安全穩定性進行了分析，研究了超固結比與安全穩定性的關系。

隧道工程；黃土隧洞；UH模型；黏聚力；變形；穩定性

0 引 言

隨著我國經濟建設及基礎設施的發展，西部地區修建了大量的鐵路與公路隧道、輸油輸氣及輸水管道和地下工程。這些工程所處土層多為黃土，土體多處于超固結狀態，在施工影響下，易風化，易滑塌，因此隧洞工程的應力變形及穩定性分析越來越受到人們的重視。國內外眾多學者對其進行了深入研究，如：鄭穎人等[1-4]將有限元強度折減法應用于土體隧洞中，對隧洞進行安全穩定分析，并提出了黃土隧洞的剪切破壞與拉裂破壞安全系數；張貴忠等[5]根據引馮濟羊工程隧洞開挖施工實踐，對黃土地區隧洞開挖襯砌技術進行了研究；大西有三等[6]和足立紀尚等[7]分別對隧洞開挖問題進行了二維彈性有限元計算。

近年來，數值計算技術發展迅速，有限元方法已成為分析隧洞工程的一種非常有效的手段。有限元法的關鍵是本構模型，若在有限元中采用合適的本構模型，就可利用有限元強大的非線性求解平臺，對隧洞工程的應力變形及穩定性進行合理分析。由姚仰平等[8-10]提出的統一硬化模型(UH模型)能夠合理考慮土的復雜應力路徑和應力歷史對土體變形和強度的影響，它不僅能夠描述正常固結土的特性，而且能夠描述超固結土的硬化、軟化、剪縮和剪脹等應力應變特性。而且它與Cam-clay模型的參數相同，可由常規三軸試驗確定，簡單、實用，利于模型在工程中的廣泛應用。

黏聚力是黃土抗剪強度的一個重要指標。若不考慮土的黏聚力，在分析隧洞開挖等工程問題時，隧洞開挖面上部土體強度會受到影響，導致坍塌，從而造成分析結果的不合理和有限元分析的不收斂問題。因此，筆者基于黏聚力c值的SMP準則，推導了考慮c值的變換應力，并在兩者的基礎上對原UH模型進行改進，建立了考慮c值UH模型，使其能考慮土的黏聚力，可用于隧洞工程問題分析。以半隱式回映算法作為應力更新算法，采用Newton-Raphson算法進行非線性問題的解答，編制了考慮c值UH模型的有限元程序。然后應用所編制的有限元程序，對無襯砌黃土隧洞工程進行了三維有限元分析，應用原UH模型、考慮c值UH模型和Mohr-Coulomb模型比較分析了隧洞周圍土體位移曲線。結果證明：考慮c值的UH模型對隧洞計算分析的合理性。并分析了隧洞周圍土體應力應變曲線，并應用有限元強度折減法對隧洞安全穩定性進行了分析，分析了不同超固結比OCR下隧洞的安全穩定系數。

1 考慮c值的SMP準則

c=0的SMP準則[11]可表示為：

I1I2/I3=C

(1)

式中：C為常數。

式(1)給出的SMP準則適用于粒狀體材料，當c≠0時，可通過坐標平移的方法轉化，如圖1。

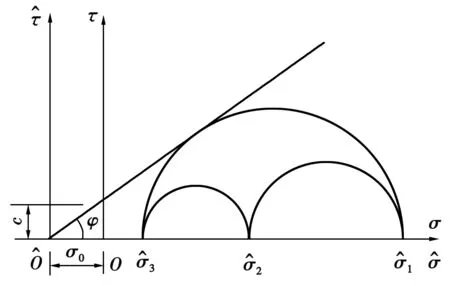
圖1 擴展SMP面上的剪應力和正應力Fig.1 Shearing stress and normal stress on the extended SMP surface

坐標平移公式為

(2)

應力不變量為

(3)

由圖1可知

σ0=c/tanφ

(4)

則考慮c值的SMP準則，可表示為

(5)

2 基于考慮c值SMP準則的變換應力

變換應力方法[12-15]假定在三軸壓縮條件下的變換應力與普通應力相同，將普通應力空間的π平面上為外凸三角形的SMP準則轉換為變換應力空間內的圓形，如圖2。圖2為θ=0°～60°范圍內的兩種屈服面。變換應力如式(6)：

(6)

式(6)為c=0情況下變換應力。當考慮c≠0情況時，變換應力為：

(7)

c=0時，原應力空間平均主應力p為

(8)

(9)

將式(2)和式(8)代入式(9)得

(10)

(11)

將式(2)、(10)、(11)代入式(7)，可得考慮c≠0下的變換應力為

(12)

圖2 變換應力Fig.2 Diagram of transform stress

3 考慮c值的UH模型

3.1 屈服函數

基于考慮c值SMP準則，在三維化的變換應力空間中采用相關聯流動法則，考慮c值UH模型屈服函數和塑性勢函數可統一表示為：

(13)

(14)

其中：

(15)

式(13)的屈服函數可寫為：

(16)

3.2 應變增量

根據廣義Hooke定律，應力增量和彈性應變增量的關系為：

dσ=Dedεe=De(dε-dεp)

(17)

式中：dεp為塑性應變增量；De為彈性剛度矩陣。

(18)

(19)

式中：ν為泊松比。

(20)

根據流動法則，塑性應變增量為

(21)

3.3 塑性因子

考慮c值UH模型的塑性因子為

(22)

式中：

(23)

(24)

3.4 彈塑性剛度矩陣

考慮c值UH模型的彈塑性矩陣為

(25)

為改善有限元分析收斂性，將切線剛度矩陣變為對稱矩陣，參照切線剛度矩陣對稱化方法[16]對彈塑性矩陣進行對稱化處理。塑性因子Λ變為

(26)

式中：

(27)

彈塑性矩陣變為：

(28)

顯然，式(28)所示彈塑性剛度矩陣是對稱的。

4 考慮c值UH模型有限元實現

4.1 非線性問題整體求解方法

應用考慮c值UH模型的有限元方法是應用Newton-Raphson算法獲得非線性問題的解答，如圖3。在非線性分析中，它是增量地施加給定的載荷，逐步獲得最終解答，并對于每一個荷載增量步，進行若干次迭代以確定一個收斂于真實解的解，整個流程融合了增量和迭代的過程[17]。每個增量步中的迭代流程如圖4。

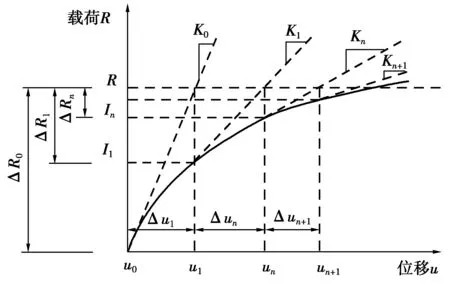
圖3 每個增量步中的迭代過程Fig. 3 Iteration process for each incremental step

圖4 每個增量步中的迭代流程Fig. 4 Iterative flow of each incremental step

4.2 應力更新算法

采用半隱式回映應力更新算法[18]，該方法關于塑性參數增量Δλ采用隱式，而關于塑性流動方向r和塑性模量D采用顯示的算法，即在步驟結束時計算塑性參數增量，而在步驟開始時計算塑性流動方向和塑性模量。

(29)

根據加卸載準則，進行彈塑性狀態的判別：

(30)

(31)

(32)

(33)

(34)

(35)

4.3 考慮c值UH模型有限元程序中OCR的引入

初始超固結比OCR是土體歷史上的最大豎向有效應力和初始豎向有效應力的比值，是反映土層天然固結狀態的一個定量指標。為研究OCR與隧洞安全穩定性的關系，可將OCR作為一個參數引入考慮c值UH模型的有限元程序，對隧洞進行有限元分析，引入流程如圖5[19]。

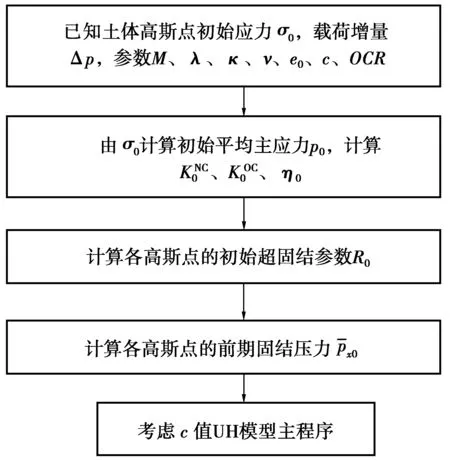
圖5 OCR引入流程Fig. 5 Flow chart of the introduction of OCR

(36)

5 無襯砌黃土隧洞有限元分析

5.1 有限元計算模型及參數

該無襯砌黃土隧洞有限元計算模型，采用三維實體模型，高為61 m，寬為51 m，隧洞高為3.5 m，跨度為3 m，矢跨比為0.5，側墻高2 m。設置邊界條件為：上表面為自由邊界，其它面為法向位移約束。采用1階8節點的三維實體單元類型(C3D8)，有限元網格如圖6(a)。考慮模型對稱性，選取隧洞周圍計算結點1～10點，如圖6(b)所示來進行分析。采用考慮c值UH模型、不考慮c值UH模型(原UH模型)和Mohr-Coulomb模型分別進行計算，計算參數[20]如表1。

圖6 網格劃分及計算節點Fig. 6 Meshing and computation nodes

參 數取 值M1λ0.158κ0.06ν0.30e01c/kPa50OCR10φ/(°)25E/MPa28.06

有限元分析步驟：

1)初始分析步，定義模型的邊界條件；

2)地壓應力場分析步，定義土體的重力，進行初始地應力平衡；

3)靜力分析步，進行隧洞的開挖，開挖總長度10 m。

5.2 結果分析

5.2.1 隧洞周圍土體位移

圖7和圖8分別為應用考慮c值UH模型、不考慮c值UH模型和Mohr-Coulomb模型計算得到的開挖后隧洞周圍土體的位移云圖和計算結點的位移量。方向3即豎直方向，方向2即水平方向。

由圖7可知，應用3種模型計算得到的位移云圖均表現出，隧洞底部和拱頂部產生的豎向位移較其余地方大，隧洞側墻部位產生的水平位移較其余地方大。比較3種模型計算的位移云圖可知，應用UH模型計算得到的位移變化影響范圍較Mohr-Coulomb模型更大一些。

由圖8可知，應用3種模型計算得到的隧洞關鍵點的位移變化規律基本相同，從總體來看UH模型所計算得到的位移較小，這是由于Mohr-Coulomb模型是理想彈塑性模型，它計算的土體一直處于彈塑性狀態，所計算產生的變形較大；而UH模型在加載時表現為彈-塑性，卸載時為彈性，所計算的變形相對較小。當用不考慮c值UH模型進行隧洞的計算分析時，計算不收斂發生中斷，說明當用不考慮c值UH模型計算的隧洞土體已經承受不了拉力作用從而發生破壞，而當用考慮c值UH模型進行隧洞計算分析時，計算收斂，說明當用考慮c值UH模型由于考慮了土體的黏聚力，從而使得計算的隧洞土體可以承受拉力作用沒有發生破壞。而且由于考慮c值UH模型考慮了土的黏聚力，提高了土體的抗剪強度，考慮c值UH模型所計算的位移較不考慮c值UH模型計算的位移小。由此說明應用考慮c值UH模型進行隧洞的計算分析較為合理。

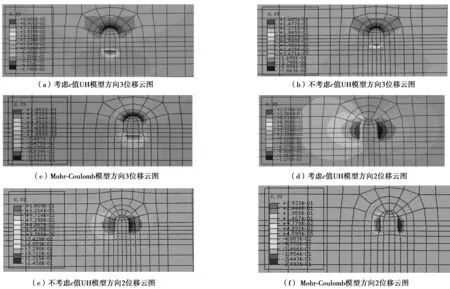
圖7 隧洞周圍土體位移云圖Fig.7 The displacement nephogram of the soil around the tunnel

圖8 隧洞周圍計算結點位移Fig. 8 The displacement of the computation nodes around the tunnel

由圖8(a)的UH模型所計算的結果可知：隧洞底部結點1～3的豎向位移為正值，說明這3個點產生向上的豎向位移，并且在底部中心點1產生最大豎向位移；側墻的結點4的豎向位移約為0，側墻和拱的結點5～10的豎向位移為負值，說明這6個點產生向下的豎向位移，并且在拱頂的點10產生最大豎向位移。由圖8(b)的UH模型所計算的結果可知，這10個點均產生正向的水平位移，點4～6的水平位移較大。由此可以得出當隧洞開挖之后，洞頂土體出現了下沉，側墻土體和洞底土體有一定程度的隆起，較大位移出現在拱頂、拱腳和洞底中央部位附近，說明這些部位是隧洞的薄弱環節和危險部位，在隧洞開挖過程中，要特別注意這些部位安全穩定情況。

5.2.2 隧洞周圍土體應力應變

圖9為應用考慮c值UH模型開挖后隧洞周圍土體剪應變云圖。圖10為開挖后土體結點的應力應變曲線，η為應力比，εv為體積應變，εd為剪應變。

圖9 隧洞周圍土體剪應變云圖Fig. 9 The shear strain nephogram of the soil around the tunnel

圖10 土體結點應力應變曲線Fig. 10 Stress-strain curves of soil nodes

由圖9可知，隧洞底部角點3和拱點8附近土體的剪應變較其余地方大。由圖10可知，點4、6的應力比遠還沒達到峰值，從趨勢來看，點6應力比峰值>點4應力比峰值>點1應力比峰值>點10應力比峰值，點1、4、6的體積應變為負值，說明在這3個點產生了明顯的剪脹現象，點10的體積應變為正值，但是有向負值轉變的趨勢，說明了該點也有剪脹現象。

5.2.3 安全穩定系數

在隧洞的安全穩定分析方面，有限元強度折減法[21]的基本原理是在隧洞的有限元計算中，通過不斷折減土體的強度參數，直到隧洞發生破壞為止，這時的折減系數即隧洞的安全穩定系數。它的具體做法是將土體的實際強度參數c和φ同時除以一個折減系數Ftrail(大于1的系數)，得到一組折減后的新系數c′和φ′值，即

(37)

將折減后的c′和φ′值作為新的材料參數代入有限元進行試算。當有限元計算收斂時，取Ftrail稍大一些后再試算，直到有限元計算不收斂時為止，這時土體達到極限平衡狀態，對應的Ftrail即為安全系數。

表2為不同OCR下應用考慮c值UH模型計算的隧洞安全系數。由表2可知：隨著隧洞土體超固結比OCR增大，安全系數也越大，這也說明了隧洞穩定性是隨著超固結比的增大而越來越高。

表2 不同OCR下隧洞安全系數

6 結 論

1)將土的黏聚力c值引入到UH模型，建立了考慮c值的UH模型，實現了原UH模型的改進，使得UH模型能夠對隧洞開挖等問題進行分析；

2)通過對無襯砌黃土隧洞開挖進行數值模擬，比較了應用考慮c值UH模型、不考慮c值UH模型和Mohr-Coulomb模型所計算的隧洞周圍土體位移曲線，得出考慮c值UH模型較合理地反映了隧洞周圍土體的變形情況；應用考慮c值UH模型對無襯砌黃土隧洞進行有限元分析，由計算所得到的位移曲線可以看出拱頂、拱腳和洞底中央部位附近土體產生較大位移，說明這些部位是隧洞的薄弱環節和危險部位，在隧洞開挖過程中，要特別注意這些部位安全穩定情況；由應力應變曲線可以看出考慮c值UH模型合理反映了黃土隧洞周圍超固結土體的剪脹現象；

3)應用有限元強度折減法對無襯砌黃土隧洞進行安全穩定性分析，得到了不同OCR下的隧洞的安全穩定系數，可以看出隨著隧洞土體超固結比OCR的增大，安全系數也越大，說明了隧洞的安全穩定性是隨著超固結比的增大而越來越高。

[1] 鄭穎人，邱陳瑜，張紅，等．關于土體隧洞圍巖穩定性分析方法的探索[J]．巖石力學與工程學報，2008，27(10)：1968-1980． ZHENG Yingren, QIU Chenyu, ZHANG Hong, et al. Exploration of stability analysis methods for surrounding rocks of soil tunnel[J].ChineseJournalofRockMechanicsandEngineering, 2008, 27(10): 1968-1980.

[2] 鄭穎人，邱陳瑜，宋雅坤，等．土質隧洞圍巖穩定性分析與設計計算方法探討[J]．后勤工程學院學報，2009，25(3): 1-9． ZHENG Yingren, QIU Chenyu, SONG Yakun, et al. Exploration of stability analysis and design calculation methods of surrounding rocks in soil tunnel[J].JournalofLogisticalEngineeringUniversity, 2009, 25(3): 1-9.

[3] 鄭穎人．有限元極限分析法在隧洞工程中的應用[J]．重慶交通大學學報(自然科學版)，2011，31(增刊2)：1127-1137． ZHENG Yingren. The application of FEM limit analysis in tunnel engineering[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2011, 31(Sup 2): 1127-1137.

[4] 向鈺周，王成，鄭穎人，等．無襯砌淺埋隧洞松散壓力的數值分析法[J]．重慶交通大學學報(自然科學版)，2012，31(3)：380-384． XIANG Yuzhou, WANG Cheng, ZHENG Yingren, et al. Numerical analysis of surrounding rock pressure on shallow buried tunnel[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2012, 31(3): 380-384.

[5] 張貴忠，付仕保，劉隹，等．淺談黃土地區隧洞開挖技術[J]．西北水資源與水工程，1998，9(1)：56-60． ZHANG Guizhong, FU Shibao, LIU Wei, et al. Introduction to tunnel excavation technology in the loess area[J].WaterResourcesandWaterEngineering, 1998, 9(1): 56-60.

[6] 大西有三，岸本英明．トンネル切羽進行の影響を近似的に考慮レた二次元有限要素解析[J]．トンネルと地下，1980，11：859-864．

[7] 足立紀尚，矢野隆夫．トンネル掘削を伴j地山變位計測結果の簡易解析法[C]．日本土木學會論文集，1987，388：207-216．

[8] YAO Yangping, HOU Wei, ZHOU Annan. UH model: three-dimensional unified hardening model for over-consolidated clays[J].Géotechnique, 2009, 59(5): 451-469.

[9] 姚仰平，侯偉，周安楠．基于Hvorslev面的超固結土本構模型[J]．中國科學(E輯)，2007，37(11):1417-1419． YAO Yangping, HOU Wei, ZHOU Annan. Constitutive model of over-consolidated clay based on improved Hvorslev envelope[J].ScienceinChina(SeriesE), 2007, 37(11):1417-1429.

[10] 姚仰平，李自強，侯偉，等．基于改進伏斯列夫線的超固結土本構模型[J]．水利學報，2008，39(11)：1244-1250． YAO Yangping, LI Ziqiang, HOU Wei, et al. Constitutive model of over-consolidated clay based on improved Hvorslev envelope[J].JournalofHydraulicEngineering, 2008, 39(11): 1244-1250.

[11] MATSUOKA H, YAO Yangping, SUN De’an. The cam-clay models revised by the SMP criterion[J].JournaloftheJapaneseGeotechnicalSocietySoilsandFoundations, 1999, 39(1): 81-95.

[12] YAO Yangping, LUO Ting, SUN De’an, et al. A simple 3-D constitutive model for both clay and sand[J].ChineseJournalofGeotechnicalEngineering, 2002, 24(2): 240-246.

[13] YAO Yangping, ZHOU Annan, LU Dechun. Extended transformed stress space for geo-materials and its application[J].JournalofEngineeringMechanics, 2007, 133(10): 1115-1123.

[14] 姚仰平，路德春，周安楠，等．廣義非線性強度理論及其變換應力空間[J]．中國科學(E輯)，2004，34(11)：1283-1299． YAO Yangping, LU Dechun, ZHOU Annan, et al. Generalized nonlinear failure theory transformed stress space for geo-materials[J].ScienceinChina(SeriesE), 2004, 34(11): 1283-1299.

[15] 姚仰平，路德春，周安楠．巖土類材料的變換應力空間及其應用[J]．巖土工程學報，2005，27(1)：24-29． YAO Yangping, LU Dechun, ZHOU Annan. Transformed stress space for geo-materials and its application[J].ChineseJournalofGeotechnicalEngineering, 2005, 27(1): 24-29.

[16] 羅汀，秦振華，姚仰平，等．UH模型切線剛度矩陣對稱化及其應用[J]．力學學報，2011，43(6)：1186-1190． LUO Ting, QIN Zhenhua, YAO Yangping, et al. Symmetrization and applications of tangent stiffness matrix for UH model[J].ChineseJournalofTheoreticalandMechanics, 2011, 43(6): 1186-1190.

[17] 朱伯芳．有限單元法原理與應用[M]．北京：中國水利水電出版社，1998． ZHU Bofang.PrincipleandApplicationofFiniteElementMethod[M]. Beijing: China Waterpower Press, 1998.

[18] 姚仰平，馮興，黃祥，等．UH模型在有限元分析中的應用[J]．巖土力學，2010，31(1)：237-245． YAO Yangping, FENG Xing, HUANG Xiang, et al. Application of UH model to finite element analysis[J].RockandSoilMechanics, 2010, 31(1): 237-245.

[19] 馮興，姚仰平，李春亮，等．UH模型在雙層地基受力變形分析中的應用[J]．巖土工程學報，2012，34(5)：805-811． FENG Xing, YAO Yangping, LI Chunliang, et al. Application of UH model to analysis of deformation of double-layer subgrade[J].ChineseJournalofGeotechnicalEngineering,2012,34(5): 805-811.

[20] 肖強，鄭穎人，葉海林．靜力無襯砌黃土隧洞穩定性探討[J]．地下空間與工程學報，2010，6(6)：1136-1141． XIAO Qiang, ZHENG Yingren, YE Hailin. Stability analysis of static unlined loess tunnel[J].ChineseJournalofUndergroundSpaceandEngineering, 2010, 6(6): 1136-1141.

[21] 陳林杰，鄭曉衛．基于有限元強度折減法的地震區三維邊坡穩定性分析[J]．重慶交通大學學報(自然科學版)，2013，32(3)：415-418． CHEN Linjie, ZHENG Xiaowei. Three-dimensional slope stability of earthquake zone based on strength reduction FEM[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2013, 32(3): 415- 418.

(責任編輯：劉 韜)

Deformation and Stability of Loess Tunnel

FENG Xing1, YAO Yangping2, HUO Haifeng1

(1. School of Airport, Civil Aviation University of China, Tianjin 300300, P. R. China; 2. School of Transportation Science and Engineering, Beihang University, Beijing 100191, P. R. China)

The stress deformation and stability analysis of the loess tunnel engineering was taken as the study objective. Firstly, on the basis of SMP criterion considering the cohesion valuec, the original UH model was improved and UH model consideringcvalue was established, which made UH model could analyze the tunnel excavation problems. Secondly, the semi-implicit return mapping algorithm was adopted to update the stress, and Newton-Raphson algorithm was adopted to solve the nonlinear problems. The finite element program of UH model consideringcvalue was compiled, and the initial over-consolidated ratio OCR as one parameter was also introduced into the finite element program. Finally, the three dimensional finite element analysis of an unlined loess tunnel was performed. The displacement of the clay around the tunnel calculated by the original UH model, the UH model consideringcvalue and Mohr-Coulomb model were compared. And the UH model consideringcvalue was used to carry out the calculation analysis of tunnel, whose rationality was declared. Furthermore, the displacement variation law of the clay around the tunnel was attained. The stress-strain law of the clay around the tunnel was studied by using the UH model consideringcvalue. In addition, the security and stability of tunnel was analyzed by using the strength reduction FEM, and the relationship between over-consolidated ratio and security-stability was studied.

tunnel engineering; loess tunnel; UH model; cohesion; deformation; stability

10.3969/j.issn.1674-0696.2017.07.04

2016-04-07；

2016-08-13

國家自然科學基金項目(11672015；51308534)；中央高校基本科研業務專項基金項目(3122014C014)；中國民航大學機場工程科研基地開放項目(JCGC2015KFJJ004)；中國民航大學科研啟動基金項目(2013QD12X)

馮 興(1980—)，女，河北石家莊人，講師，博士，主要從事巖土工程方面的研究。E-mail：fxing_sjz@foxmail.com。

U451；TU43

A

1674-0696(2017)07-021-08