基于模糊信息粒與SVM的道路交通狀態波動分析

陸百川,李曉璐,郭桂林,黃梨力

(1. 重慶交通大學 交通運輸學院，重慶 400074；2. 重慶交通大學 重慶山地城市交通系統與安全實驗室，重慶 400074)

?

基于模糊信息粒與SVM的道路交通狀態波動分析

陸百川1,2,李曉璐1,郭桂林1,黃梨力1

(1. 重慶交通大學 交通運輸學院，重慶 400074；2. 重慶交通大學 重慶山地城市交通系統與安全實驗室，重慶 400074)

為分析道路交通狀態波動范圍，提出了一種基于模糊信息粒化與支持向量機組合預測的建模方法。分析了道路交通狀態波動特點和交通參數選擇原則，以模糊理論和時間序列預測為基礎，通過模糊信息粒以15 min時間窗將樣本數據模糊化，得到Low、R、Up這3組時間序列；并利用支持向量機模型分別對其進行預測，獲得道路交通狀態的波動范圍與變化趨勢。實例分析時，在驗證數據采集路段屬性相近的前提下，用該組合模型對早、晚高峰和平峰等3個時段的交通波動狀態進行驗證，驗證結果有較高精度，能有效預測交通狀態波動情況。

交通工程；交通狀態；波動范圍；模糊信息粒化；支持向量機

0 引 言

對交通狀態的波動進行準確估計與分析能夠為相關部門有針對性地制定交通管控措施提供可靠依據，提高路網的利用率，保障道路交通更加通暢；同時也將為出行者提供路段交通狀態變化趨勢，從而合理規劃出行路線。隨著信息技術的發展，通過對海量的道路交通數據挖掘，分析道路交通狀態波動范圍成為當前的研究熱點之一。

劉曉玲等[1]在對多維時空參數進行分析的基礎上，提出利用支持向量機(SVM)對不同維數的路段交通狀態進行短時預測；董宏輝等[2]通過提取對道路交通狀態有顯著影響的時空特征，利用最大熵模型訓練獲得不同影響特征的權重，從而對路段交通狀態等級進行直接預測；劉擎超等[3]通過構建神經網絡分類器的能力區域，通過計算樣本數據與交通狀態類簇之間的空間距離，對道路交通狀態進行預測；錢民等[4]提出了一種從系統的角度出發，通過定性動態概率網絡方法對交通狀態進行預測及改進；康海貴等[5]提出基于混沌Logistic映射和云自適應機制對標準的遺傳算法進行改進，建立了基于混沌云自適應遺傳算法進行SVR參數優選CCLGA-SVR城市主干道短時交通流量預測模型。上述研究多以提高狀態預測的準確性為主，若可對交通狀態變化范圍進行有效預測，則能提前評估其對路網造成的影響，從而使交通管理部門采取有效措施分擔路網交通壓力。

目前對道路交通狀態的研究只是停留在點時間的預測，而忽視了交通狀態的波動情況，筆者提出了基于模糊信息粒化和SVM的預測模型對交通狀態波動進行分析。首先，以15min為操作窗口，利用三角型模糊信息粒將樣本數據模糊化，得到Low、R、Up等3組時間序列；然后分別以Low、R、Up作為輸入，通過支持向量機模型分別對其進行預測，從而獲得路段交通狀況的波動范圍及其變化趨勢；最后，經重慶市龍騰大道部分路段實測數據仿真分析，證明了筆者提出模型的有效性。

1 交通狀態波動特征與參數選擇

1.1 交通狀態波動特征

交通狀態波動是指在一定時間內交通狀態變化的范圍，交通狀態波動分析可從不同層次、不同維度定量地分析交通流運行的狀況，能夠有效的識別交通流運行中的薄弱環節，掌握交通流演變的規律，為交通管理部門制定合理的交通管控措施提供可靠依據。

交通狀態波動反映的是某路段整個交通流運行的情況，通常交通狀態波動變化具有以下幾個特征：

1)時間屬性。交通狀態波動是交通流在一段時間內運行變化的客觀反映，在相同路段，不同時間交通狀態波動也不盡相同，具有時間屬性。

2)空間屬性。交通狀態波動隨空間變化而變化，在相同時間，不同路段交通狀態波動也不盡相同，具有空間屬性。

3)對象屬性。交通狀態波動是從宏觀層面分析交通情況，是以路段中所有交通流為一個整體而言。

4)條件屬性。交通狀態波動反映的是交通流的運行情況，只有交通流行為改變才能產生新的交通狀態波動。

5)結果屬性。交通狀態波動是衡量交通流運行優劣的定量指標，可以根據交通流行為預測波動范圍，具有可預測性。

1.2 交通參數選擇原則

選擇合理且可靠的交通參數進行路段交通狀態的預測，不僅減少了前期數據處理的工作量，同時能夠提高后續預測模型的精度。筆者通過以下幾個原則進行交通參數的選取：

1)直觀性。即交通參數的變化容易被覺察和理解。如：車速，當行駛路段暢通時，車輛能夠以較快的速度通行；反之，車輛行駛緩慢；

2)便捷性。即所選交通參數能夠直接獲取。如：密度，該參數直觀性較好，然而，目前的檢測技術，只能通過計算間接得到該參數。這樣不僅增加數據準備的工作量，還使實時性大打折扣；

3)靈敏性。即所選的交通參數對當下的交通狀態反映迅速，大體上能實時響應道路交通狀態的波動變化。

考慮上述3個原則的分析，交通流速度參數能夠及時、直觀地反映交通狀態的變化情況。故而，筆者以交通流速度為研究對象，對交通狀態的波動及其變化趨勢進行分析。

2 交通狀態波動需求

交通狀態波動分析是以交通流理論為基礎，研究交通流的時空變化特征。通過對交通狀態波動分析，可以發現交通流運行模式及變化規律，以便建立相應模型深入研究。

從需求者角度而言，交通狀態波動分析主要服務于兩類需求者，一類是交通出行者，如乘客和駕駛員；另一類是交通管理者，如交通管理部門、公交公司，道路建設部門等。兩類需求者對交通狀態波動分析功能需求如表1。

表1 不同對象交通信息需求分析

交通管理者通過對交通流運行情況進行分析、判斷及預測，從而采取相應措施，影響出行者的交通行為。同時，出行者通過獲取的交通狀態波動情況，選擇合適的出行路線、出行時間及出行方式，以致于又影響了交通流運行狀況。因此，兩者相互聯系，又相互影響。由表1中兩者需求目的可以看出：交通出行者更關注個體的出行成本，通過對交通狀態波動情況分析，選擇適當的出行路線，使得自身的出行延誤最小；而交通管理者更注重整個路網的運行情況，通過分析交通狀態波動情況，及時、科學地制定交通管控措施，最大限度的提高路網的利用率。

同時，對交通狀態波動情況的分析，將道路交通狀態識別由點擴展到了面。一般地，預測道路交通狀態都是通過分析歷史交通數據，建立數學模型，然后對點時間的預測。然而，出行者的出行時間通常是模糊的，是在一個時間段內。因此，精確時間點交通狀態預測的應用就受到了很大的限制。而分析交通狀態波動情況，則可將交通狀態的判斷由點時間拓展到一個時間段內，通過分析一定時間段的交通狀態波動范圍，從而為交通出行者和管理者的決策提供依據，提高了交通狀態預測的價值。

3 模糊信息粒化和SVM原理

3.1 模糊信息粒化

L．A．ZADEH[6]提出了信息粒化的概念，其核心思想為：通過分析事物內部特征，將屬性相似，功能相同的部分視為一個個體，從而將整體劃分為多個個體，這些個體稱為信息粒。其本質就是將事物整體劃分為獨立的個體進行研究。

在實際采集的交通數據中通常存在不同的數據類型，表征的屬性也不同，往往很難用特定的模型對其進行表示。模糊信息粒化用模糊集的形式表達信息粒，通過模糊集的方法對時間序列進行信息粒化，主要分為兩個過程：窗口劃分和模糊化。所謂窗口劃分，即將給定的一段完整的時間序列按實際需求的時間間隔劃分為若干子序列，作為操作窗口；模糊化處理，即將操作窗口中的數據進行模糊處理，生成相應模糊集，結合上述兩個過程就是模糊信息粒化[7]。

目前實際分析中常用的模糊信息粒形式有：三角型、梯形、高斯型和拋物線型等，不同模糊信息粒形式如圖1。

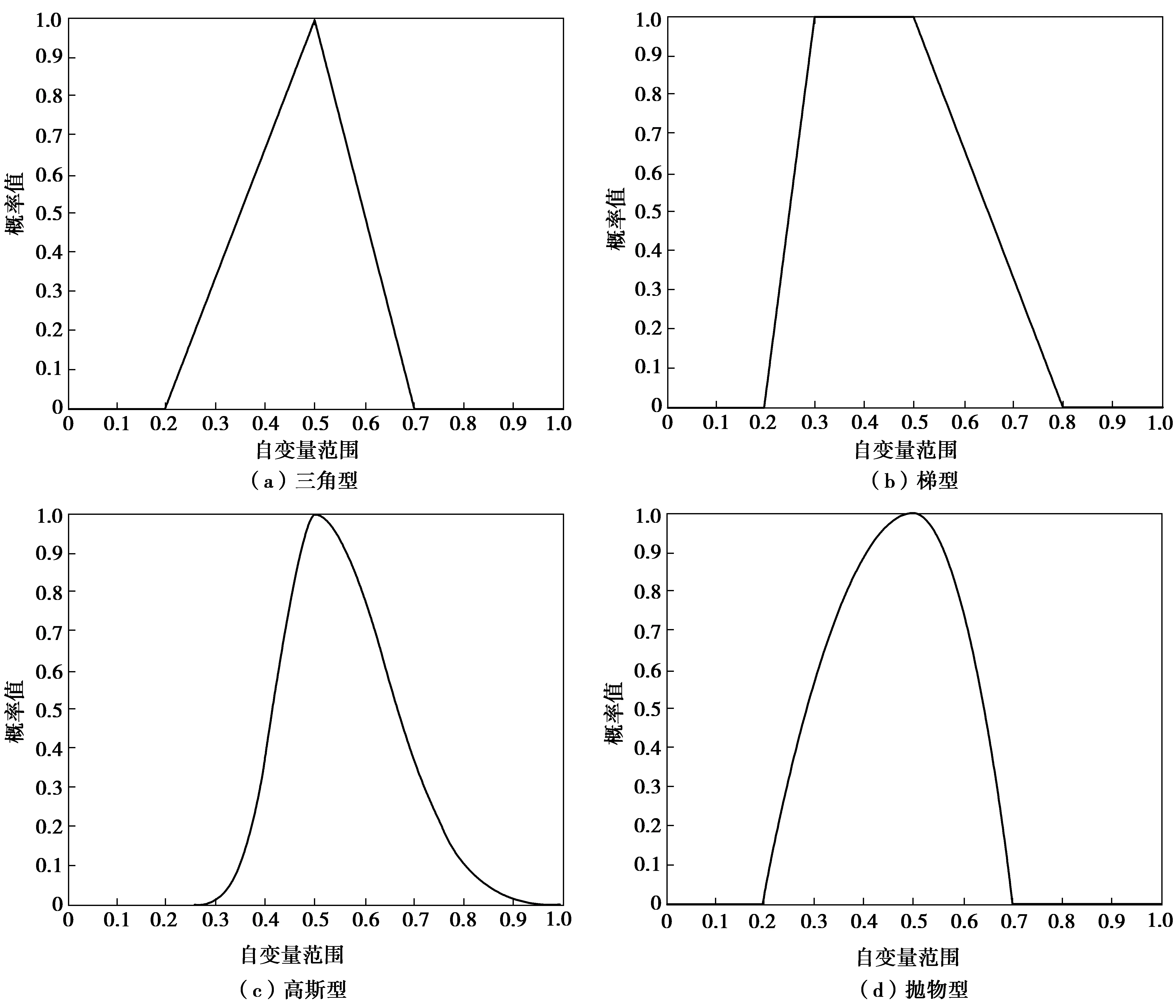
圖1 不同模糊信息粒隸屬度函數Fig. 1 Different membership functions of fuzzy information granules

3.2 支持向量機

交通流速度序列具有高度的非線性、復雜性和隨機性，若以傳統的數學方法來對其進行趨勢預測，往往難以滿足后續應用的要求。支持向量機(support vector machines，SVM)具有以下幾個方面優勢：

1)理論基礎完善。以統計學為理論基礎，具有較強的學習能力。

2)能夠獲得全局最優解。該方法將傳統優化問題轉化成對凸二次規劃的求解問題，其中，二次規劃問題的解通常是唯一的全局最優解，避免了局部最優解的困擾。

3)結構風險最小原則。該原則提高了模型的泛化能力，在各領域有廣泛的應用。

4)克服了維數災難。通過核函數學習機制，在分析非線性、高維模式識別問題時很大程度上克服了“維數災難”和“過學習”等問題。

4 交通狀態波動范圍預測模型

模糊信息粒化是將一個整體中屬性相似、功能相近的個體劃分在同一操作窗口內，利用個體間的信息共享和相互協作找出最優解[8]；支持向量機以結構風險最小化原則，在小樣本、隨機性較強的時間序列預測中有突出的表現，結合兩者的優勢，針對交通狀態波動范圍分析，建立基于模糊信息粒化與支持向量機的組合預測模型。

4.1 交通流速度數據模糊化

4.1.1 窗口劃分

在構建模糊信息粒子之前，需要選擇一定長度的窗口，將原始時間序列劃分為多個小的子序列，由于窗口長度的確定存在一定的主觀性，不同的劃分方式對實際的預測也會產生不同的影響。根據交通狀態波動特征，以15 min時間窗將樣本數據進行分割，設置操作窗口的長度為3，即每個粒化窗口中包含3個周期的數據，那么，原數據長度除以3后取整為最終粒化窗口個數。

4.1.2 數據模糊化處理

在每個子序列窗口建立模糊粒子是模型中的關鍵。由于筆者要對道路交通狀態波動范圍進行分析預測，通過窗口內的最大值和最小值信息能夠獲得波動區間。故而筆者選取三角型模糊信息粒對數據進行處理，其隸屬度函數表示為：

(1)

式中：x為論域中的變量；a、m、b分別為各窗口進行模糊信息粒化處理后所得3個變量Rlow、Raverage和Rup參數，其中RLow表示交通狀態波動的最小值，Raverage表示交通狀態波動的平均值，Rup表示交通狀態波動的最大值。

采用三角型模糊信息粒計算參數Rlow，得到交通狀態波動最小值。

(2)

采用三角型模糊信息粒計算參數Raverage，得到交通狀態波動平均值。

(3)

采用三角型模糊信息粒計算參數Rup，得到交通狀態波動最大值。

(4)

4.2 支持向量機預測過程

4.2.1 樣本數據預處理

為避免數值較大的數據覆蓋數值較小的數據情況的發生，使得數據之間具有可比性，需要對訓練數據進行預處理。首先分別對模糊信息粒化后得到的交通狀態波動最小值Rlow、平均值Raverage和最大值Rup進行歸一化處理[9]，如式(5)：

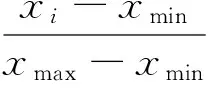
(5)

式中：xmin為原始數據最小值；xmax為原始數據最大值；xi為原始數據；pi為歸一化后的數據。

4.2.2 模型參數確定

由于SVM屬于“黑箱操作”模式，難以直接求得最優解，因此，采用模式搜索算法，訓練SVM，并確定最優參數C和g，構建交通狀態波動預測模型。

4.2.3 模型預測

利用最優參數C和g建立SVM預測模型，以預測數據為輸入，預測下一個時間窗口內交通狀態波動的最小值Rlow、平均值Raverage和最大值Rup。

4.2.4 檢驗模型預測效果

對SVM的預測結果進行分析，分析預測值與真實值的誤差情況，評估預測模型的優劣。

4.3 分析交通狀態波動范圍

由SVM回歸模型分別對模糊粒子參數Rlow，Raverage和Rup進行預測，從而得到交通狀態波動的最小值、平均值和最大值，分析3者之間的關系，進而確定交通狀態波動范圍。

基于模糊信息粒化的SVM組合預測模型預測過程如圖2。模糊信息粒化以粒子為單位處理信息，通過對交通流速度數據進行有效挖掘，并以挖掘得到的有效數據建立交通狀態波動預測模型。

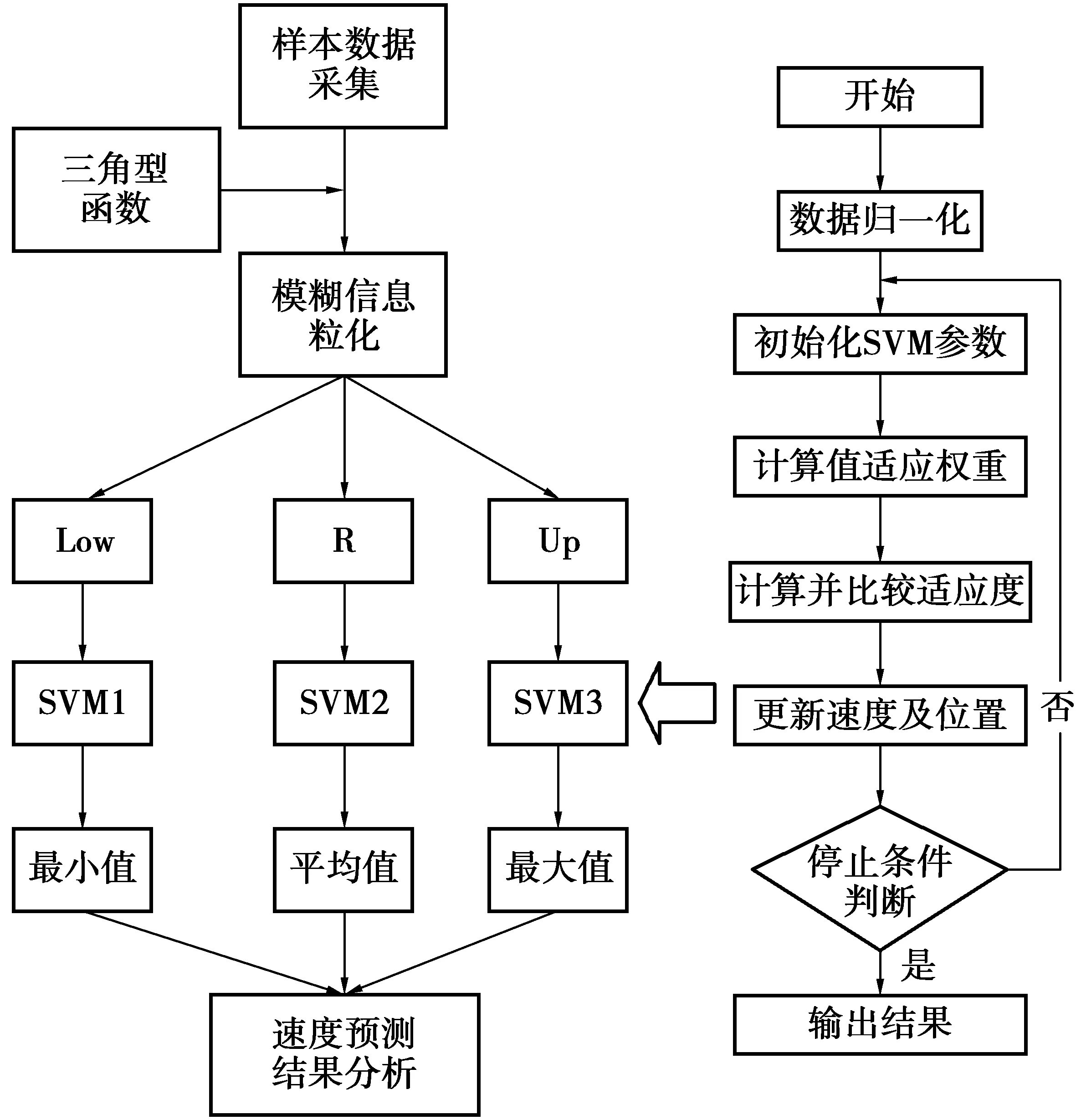
圖2 基于模糊信息粒化的SVM組合模型流程Fig.2 Flow chart of the combined model based on fuzzy information granulation and SVM

5 案例分析

5.1 路段屬性相似性分析

筆者選取了重慶市龍騰大道，它是重慶市主干道之一，約為4 km，途經陳家坪立交、大公館立交、謝家灣立交和多個交叉口，雙向6車道。首先以交叉口為節點簡單將干道分為5段： 陳家坪立交—科園四路—科園六路—大公館立交—謝家灣立交—鵝公巖大橋。然而，簡單的以交叉口為節點的分段方式并不合理，這里文章選取了道路固有屬性，如路段長度、路面情況、坡度、車道數和路段動態影響因素，如路段平均行駛速度，道路的交通管控措施等，進一步將各路段以屬性相似性為依據進行重新聚類。具體步驟為：①對選取的各影響因素進行歸一化處理，如表2；②構建5個行向量，向量分別為各路段影響因素歸一化后的數據；③計算各向量間距離同時進行聚類，并繪制聚類譜系圖。

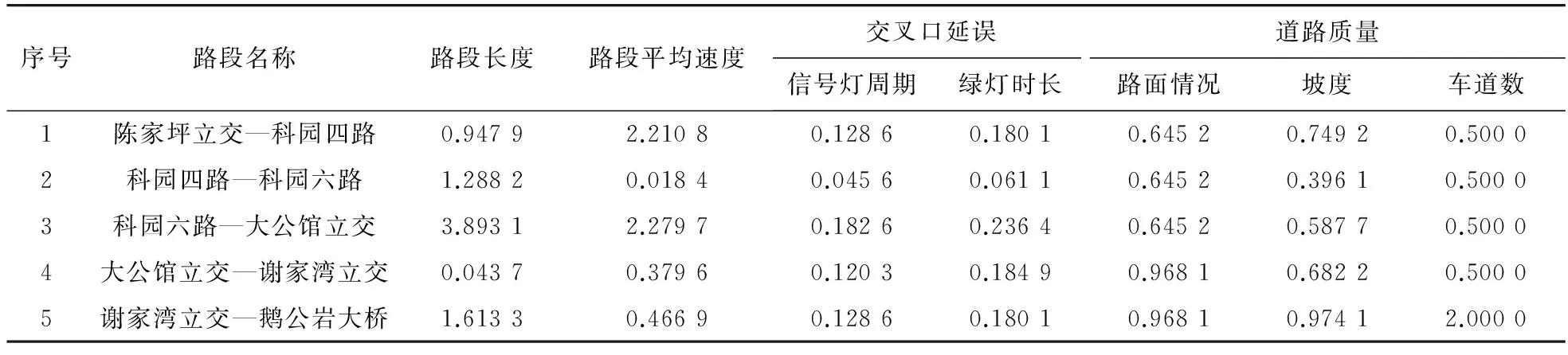
表2 各影響因素數據歸一化結果

在SPSS統計軟件中，將5組行向量以組間聯接的方式進行系統聚類，用平方Euclidean距離作為度量標準，根據路段各不同影響因素進行聚類分析，得到聚類譜系數圖，如圖3。由路段間各屬性相似性為依據，將龍騰大道各路段分為3類：路段2、4、5；路段1；路段3。

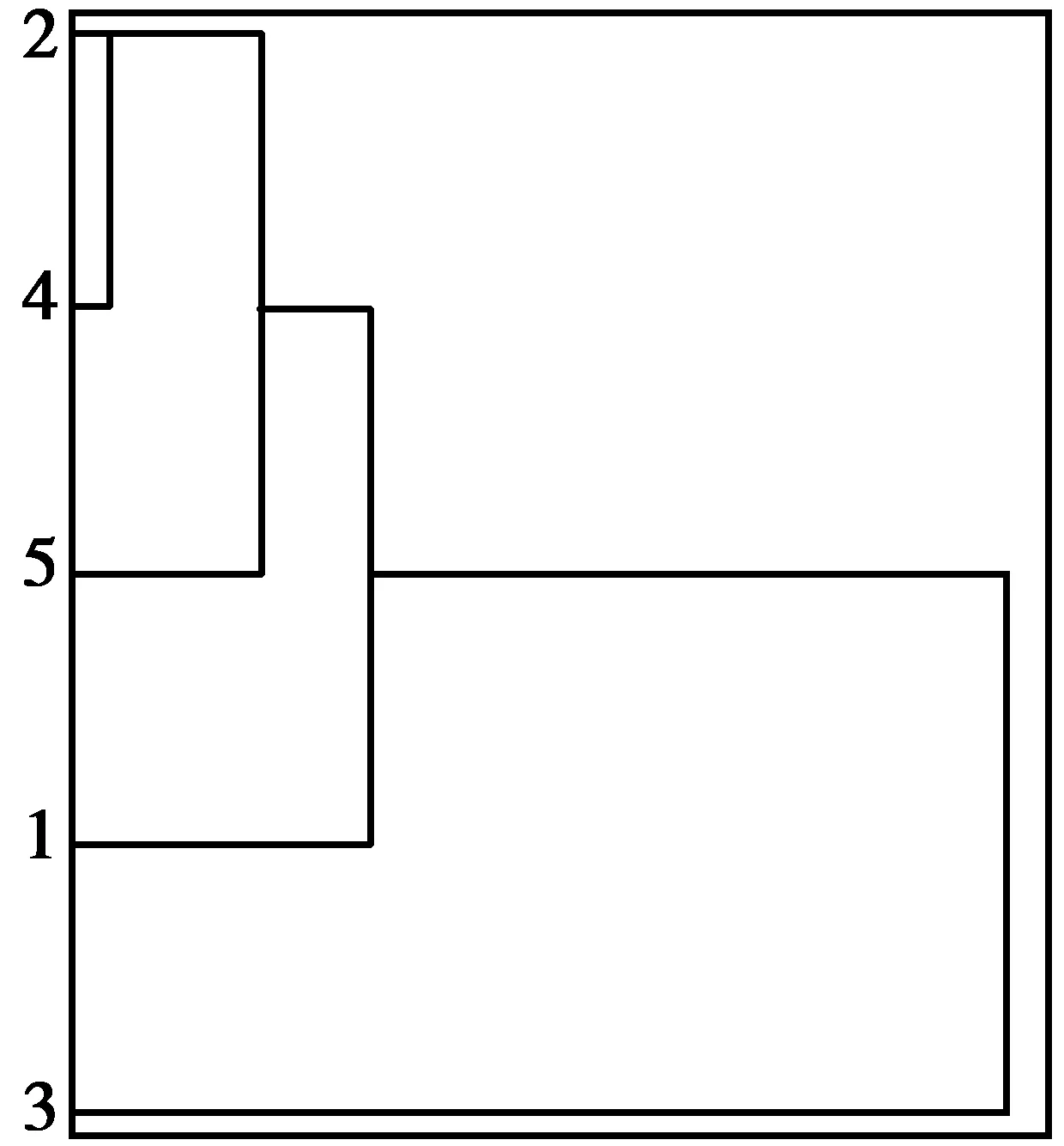
圖3 路段聚類譜系圖Fig. 3 Cluster spectrum diagram of road segment

顯然，考慮多因素后將龍騰大道以相似性分為3類的路段分類方式比單一的以交叉口為節點分段方式減少了計算量，同時，由于聚類時考慮了路段上的動靜態因素，因此在理論上更具有可信度。所以筆者選取聚類后的分段結果來對所提出的模型進行驗證。

5.2 數據準備與結果分析

筆者進一步選擇3段中的一段，科園六路—大公館立交，2014年12月15日—19日的出租車GPS數據為基礎。由于所采集數據的時間屬性有較大變化，分為3個時段“早高峰時段—平峰時段—晚高峰時段”進行分析，數據以5 min為周期，以前4 d的3個時段的數據作為訓練樣本，19日的數據作為預測樣本。模糊信息粒化以3為數據窗口長度，即以3個周期為一個操作窗口。前4 d每個時段的數據均被分成了96個時間窗口，分別對每個時段時間窗口的數據進行驗證。限于篇幅，在每個時間段內，筆者分別隨機抽取兩個時間窗口記為win_num1，win_num2。通過三角型模糊粒子對交通流速度序列進行信息粒化處理，得到3組時間序列Rlow、Raverage和Rup，如圖4。

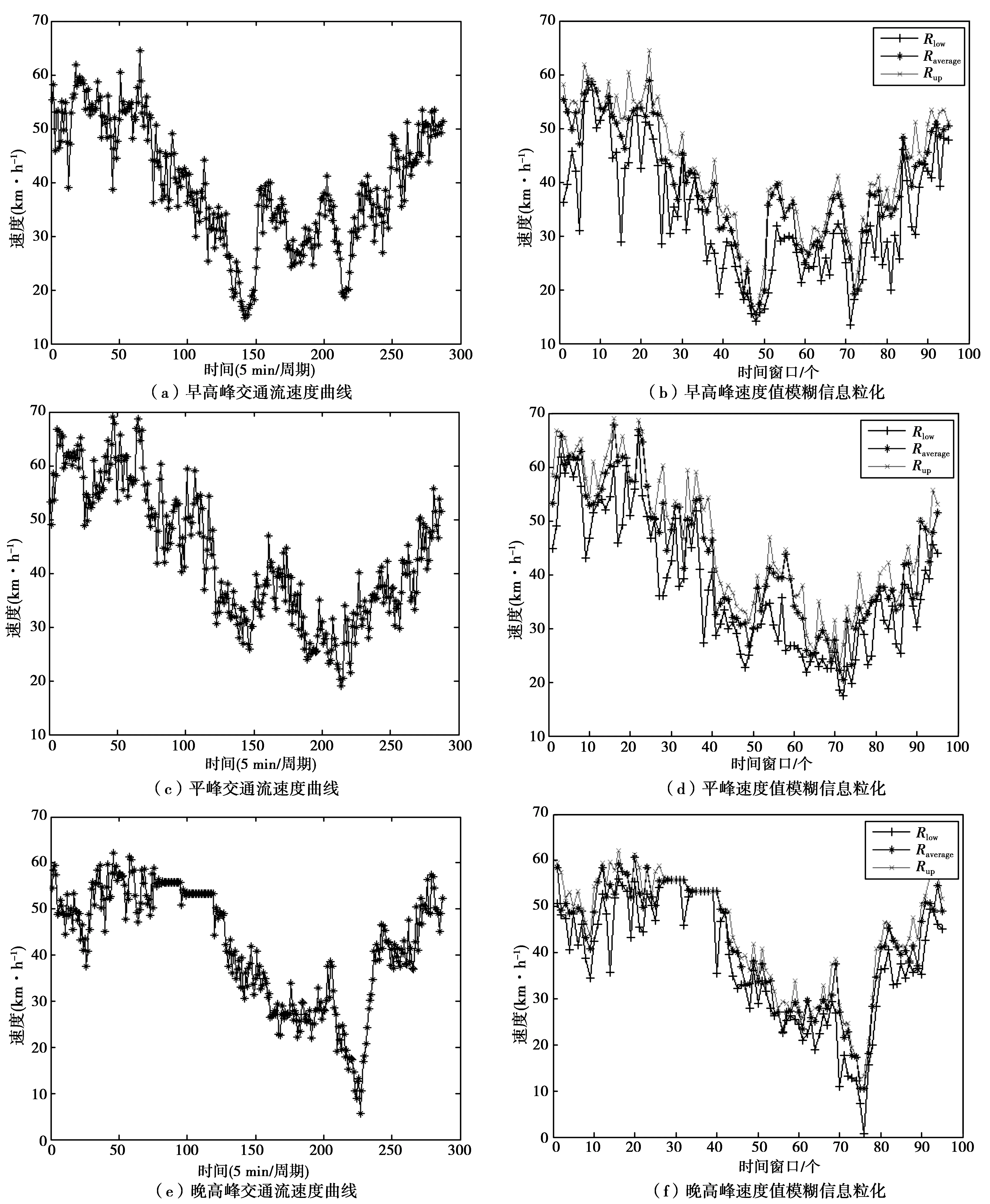
圖4 交通流速度曲線與速度值模糊信息粒化Fig. 4 Traffic flow velocity curve and fuzzy information granulation of traffic flow velocity

圖4中：當車輛在路段上勻速行駛時，將其進行模糊信息粒化處理后，獲得的Rlow、Raverage和Rup這3個參數的值高度吻合，表明該時段內交通運行穩定，交通流速度沒有明顯波動。而當道路上交通流速度明顯變化時，其模糊信息粒化后所得的Rlow、Raverage和Rup這3參數值也有明顯波動。

依次分別將3個時段速度值進行模糊信息粒化處理后得到的Rlow、Raverage和Rup三序列分別作為SVM的輸入，同時，對SVM模型進行參數尋優，最后利用此模型對路段交通狀態短時變化趨勢進行預測。限于篇幅，筆者選擇早晚高峰對所提模型進行驗證，同時為了說明文中提出模型的有效性，在使用同樣的樣本數據條件下，在模糊信息粒化后使用Elman神經網絡進行相應的回歸預測，其預測結果見表3。

根據表3可知，基于模糊信息粒的SVM模型能夠準確地描述速度波動范圍。就晚高峰時段，將時間窗口win_num1和win_num2中實際數據由小到大排列，分別為[50.290 1 54.496 4 56.995 3]、[45.062 3 49.112 3 49.803 0]。參數Rlow、Raverage和Rup準確地對實際交通流速度波動范圍進行了描述，窗口win_num1的預測結果中下限溢出即路段交通狀態有惡化趨勢，而窗口win_num2的預測結果中上限溢出，說明路段交通狀態未達到最佳狀態，仍有較大的改善空間。在時間窗口win_num1內，交通狀態波動范圍為9.33 km/h；而在時間窗口win_num2內，交通狀態波動范圍為10.49 km/h。在這兩個時間窗口內，道路交通運行穩定，波動較小。同理可以分析早高峰時段和平峰時段的交通狀態波動情況。

通過對比SVM和Elman預測結果可知，在早高峰兩個時間窗口內SVM對Rlow、Raverage和Rup預測其平均誤差分別為0.497%、2.541%、0.875%；而Elman預測結果平均誤差分別為1.621%、3.184%、2.064%。

在晚高峰兩個時間窗口內SVM對Rlow、Raverage和Rup預測其平均誤差分別為1.715%、2.189%、3.744%，而Elman預測結果平均誤差分別為4.029%、5.096%、2.319%。由此可見，筆者提出的模型具有更高的精度。

表3 SVM和Elman預測結果對比

6 結 論

筆者對道路交通狀態波動情況進行了研究，分3個時段“早高峰時段—平峰時段—晚高峰時段”進行分析。

首先，以模糊集理論為基礎，以3個周期數據為操作窗口，利用三角型模糊信息粒將樣本數據模型化，得到分別表示交通狀態變化的最小值Rlow、平均值Raverage和最大值Rup；之后將Rlow、Raverage和Rup作為SVM模型和Elman神經網絡的輸入，并對SVM進行參數尋優，得到交通狀態波動情況；最后經實例分析，比較SVM模型和Elman神經網絡預測結果可知：筆者所提出的模型具有更高的預測精度，能夠有效預測交通狀態波動范圍。

[1] 劉曉玲，賈鵬，鄔珊華，等．基于多維時空參數的道路短期交通狀態預測[J]．交通運輸系統工程與信息，2011，11(4)：140-146． LIU Xiaoling, JIA Peng, WU Shanhua, et al. Short-term traffic flow forecasting based on multi-dimensional parameters [J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2011, 11(4): 140-146.

[2] 董宏輝，賈利民，孫曉亮，等．基于最大熵模型的城市快速路交通狀態預測方法研究[J]．交通運輸系統工程與信息，2010，10(2)：112-116． DONG Honghui, JIA Limin, SUN Xiaoliang, et al. Traffic state forecasting towards urban freeway based on the maximum entropy model [J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2010, 10(2): 112-116.

[3] 劉擎超，陸建，陳淑燕．基于能力區域的交通狀態預測方法[J]．物理學報，2014，63(14)：94-101． LIU Qingchao, LU Jian, CHEN Shuyan. Traffic state prediction based on competence region [J].ActaPhysicaSinica, 2014, 63(14): 94-101.

[4] 錢民，唐克生．基于定性動態概率網絡的交通狀態預測及改進[J]．云南大學學報(自然科學版)，2012，34(2)：165-168． QIAN Min, TANG Kesheng. Traffic state prediction and improvement based on qualitative dynamic probabilistic networks [J].JournalofYunnanUniversity(NaturalSciencesEdition), 2012, 34(2): 165-168.

[5] 康海貴，莫仁杰，李明偉，等．基于云遺傳算法優選的SVR交通量預測模型[J]．武漢理工大學學報(交通科學與工程版)，2013，37(2)：225-229． KANG Haigui, MO Renjie, LI Mingwei. Urban traffic flow forecasting base on CCLGA algorithm optimizes parameters of SVR [J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering), 2013, 37(2): 225-229.

[6] ZADEH L A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic [J].FuzzySetsandSystem, 1997, 90(2): 111-127.

[7] PEDRYCY W.GranularComputing:AnIntroduction[M].Dodrecht: Kluwer Academic Publishers, 2003.

[8] 彭勇，陳俞強．基于信息粒化的SVM時序回歸預測[J]．計算機系統應用，2013，22(5)：163-167． PENG Yong, CHEN Yuqiang. Time series regression and prediction based on information granulation and SVM [J].ComputerSystems&Applications, 2013, 22(5): 163-167.

[9] 黃艷國，許倫輝，鄺先驗．基于模糊C均值聚類的城市道路交通狀態判別[J]．重慶交通大學學報(自然科學版)，2015，34(2)：102-107． HUANG Yanguo, XU Lunhui, KUANG Xianyan. Urban road traffic state identification based on fuzzy C-mean clustering [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2015, 34(2): 102-107.

[10] 史峰，王輝，胡斐，等．MATLAB智能算法30個案例分析[M]．北京：北京航空航天大學出版社，2011． SHI Feng, WANG Hui, HU Fei, et al. 30IntelligentAlgorithmCaseAnalysisBasedonMATLAB[M]. Beijing: Beihang University Press, 2011.

[11] 田保慧，郭彬．基于時空特征分析的短時交通流預測模型[J]．重慶交通大學學報(自然科學版)，2016，35(3)：105-109． TIAN Baohui, GUO Bin. A short-term traffic flow prediction model based on spatio-temporal characteristics analysis [J].JournalofChongqingJiaotongUniversity(NatureScience), 2016, 35(3): 105-109.

(責任編輯：劉 韜)

Fluctuation Analysis on Road Traffic State Based on Fuzzy InformationGranulation and Support Vector Machine

LU Baichuan1, 2, LI Xiaolu1, GUO Guilin1, HUANG Lili1

(1. School of Traffic & Transportation, Chongqing Jiaotong University, Chongqing 400074, P. R. China;2. Key Lab of Traffic System & Safety in Mountain Cities, Chongqing Jiaotong University, Chongqing 400074, P. R. China)

In order to analyze the range of traffic state fluctuation, a combined modeling method of forecasting the range of traffic state fluctuation based on fuzzy information granulation and support vector machine was put forward. The fluctuation characteristics of road traffic state and the selection principles of traffic parameters were analyzed on the basis of fuzzy theory and time series prediction. The sample data were fuzzed by 15 min time window through the fuzzy information granules, and three sets of time series, including Low, R and Up, were obtained. The support vector machine was used to forecast each set of time series, and the traffic state fluctuation range and variation tendency were obtained. In case studies, in the premise of verification data acquisition segment with similar attributes, the proposed model was used to analyze the fluctuation of traffic state in morning, evening peak periods and peace period, whose results were of high accuracy and could effectively predict the fluctuation of traffic state.

traffic engineering; traffic state; fluctuation range; fuzzy information granulation; support vector machine

10.3969/j.issn.1674-0696.2017.07.14

2016-05-02；

2016-09-07

陸百川(1961—)，男，江蘇南通人，教授，博士生導師，主要從事交通信息工程及控制方面的研究。E-mail：baichuan@cqjtu.edu.cn。

李曉璐(1992—)，女，新疆烏魯木齊人，碩士研究生，主要從事交通信息工程及控制方面的研究。E-mail：rolista1120@163.com。

U491.1+23

A

1674-0696(2017)07-083-07