領導-跟隨多智能體系統的部分分量一致性?

吳彬彬1)2) 馬忠軍1)2)? 王毅3)

1)(桂林電子科技大學數學與計算科學學院,桂林 541004)

2)(桂林電子科技大學,廣西高校數據分析與計算重點實驗室,桂林 541004)

3)(浙江財經大學數學與統計學院,杭州 310012)

(2016年6月29日收到;2016年11月30日收到修改稿)

領導-跟隨多智能體系統的部分分量一致性?

吳彬彬1)2) 馬忠軍1)2)? 王毅3)

1)(桂林電子科技大學數學與計算科學學院,桂林 541004)

2)(桂林電子科技大學,廣西高校數據分析與計算重點實驗室,桂林 541004)

3)(浙江財經大學數學與統計學院,杭州 310012)

(2016年6月29日收到;2016年11月30日收到修改稿)

首先給出多智能體系統的部分分量一致性概念,然后探討有向網絡拓撲結構下的一階非線性領導-跟隨多智能體系統的部分分量一致性問題.通過設計合適的牽引控制器,建立相應的誤差系統,將多智能體系統的部分分量一致性轉化為誤差系統的部分變元穩定性,并運用矩陣理論和穩定性理論,導出該多智能體系統實現部分分量一致性的充分條件.數值模擬驗證了理論結果的正確性.

多智能體系統,一致性,部分分量一致性

1 引 言

近年來,隨著人工智能技術的快速發展,多智能體系統的研究引起了物理、通信與控制等各領域學者的興趣.一致性作為多智能體系統協調控制中最基本的問題之一,也受到多個領域中研究者的持續關注[1?4].一致性是指由多個智能體組成的一個系統在控制協議的作用下,其位置或速度等狀態變量漸近趨同.多智能體系統的一致性研究[5,6]在蜂擁問題、群集問題、編隊控制和分布式傳感器網絡等領域都有著廣泛應用.

目前,已有很多研究無領導者的多智能體系統一致性問題的文獻[7?12].例如,文獻[7]將系統的通信拓撲建模成有向圖,首先證明了在有向固定拓撲強連通的情況下,系統能夠達到一致;文獻[8]考慮了廣義的線性和非線性多智能體系統的一致性問題;文獻[9]考察了同時具有通信時延和輸入時延的一階與二階多智能體系統的運動一致性問題.此外,文獻[10,11]分別考慮了一階和二階非線性多智能體系統模型的一致性問題;通過給出一個新的李雅普諾夫函數,文獻[12]獲得了固定通信拓撲結構下的三階非線性多智能體系統一致性的一個充分條件.領導-跟隨多智能體系統的一致性問題也獲得了一些研究成果[13?17].例如,文獻[13]考察了有向網絡拓撲結構下非線性多智能體系統的局部和全局一致性問題;基于一個新的T-S模糊模型方法,文獻[14]考慮了在任意拓撲結構下非線性多智能體系統模型的H∞一致性控制問題;運用線性矩陣不等式方法,文獻[15]在其基礎上獲得了領導-跟隨多智能體系統模型一致性的一個模糊算法;文獻[16]研究了在固定和切換拓撲結構下高階多智能體系統的一致性問題;此外,文獻[17]提出了多智能體系統的滯后一致性,并基于矩陣理論和穩定性理論,給出了幾個實現滯后一致性的充分條件.

以上研究考慮的一致性(或聚類一致性)是所有(或部分)智能體的所有狀態變量(如位移和速度)漸近趨于恒同.一些學者從另外的角度,針對二階多智能體系統,研究了部分狀態變量的一致性問題.例如,文獻[18]研究了二階多智能體系統的部分狀態一致性問題,這意味著每個智能體的部分狀態(如速度)達到一致,其他的狀態(如位移)不一定達到一致.然而,在多智能體網絡中,因為一些因素或需要,系統中智能體的位移(或速度)也許只在某一個方向上的分量達到一致,而在其他方向上的分量并不一定一致.例如,飛機在飛行表演時,幾架飛機保持一字橫隊并排(或射線狀)飛行,就位移這個三維矢量來說,在其飛行前進方向上的位移分量是一致的,而位移在另外方向上的分量并不是一致的.從本質上來說,這就是一種關于位移的部分分量一致性問題.受上述研究結果和現象的啟發,本文考慮多智能體系統的部分分量一致性問題.與狀態中全部分量達到一致的已有研究結果相比較,部分分量一致性更具有一般性,是一種比通常意義下的一致性要弱的群體動力學行為.因此,部分分量一致性的研究具有較強的理論意義和潛在的應用價值.

本文第2節給出文中要用到的部分變元穩定性、圖論以及矩陣相關知識和引理;第3節先給出部分分量一致性概念,然后研究領導-跟隨非線性多智能體系統的部分分量一致性問題,通過設計合適的控制項,并運用矩陣理論和穩定性理論,導出該多智能體系統實現部分分量一致性的充分條件;第4節數值模擬驗證了理論結果的正確性;第5節給出結論和討論.

2 預備知識

首先給出文中要用到的有關穩定性理論的一些結果.考慮n維非自治常微分方程組

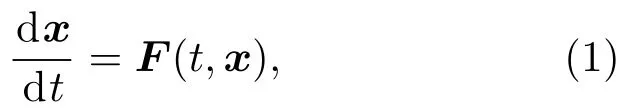
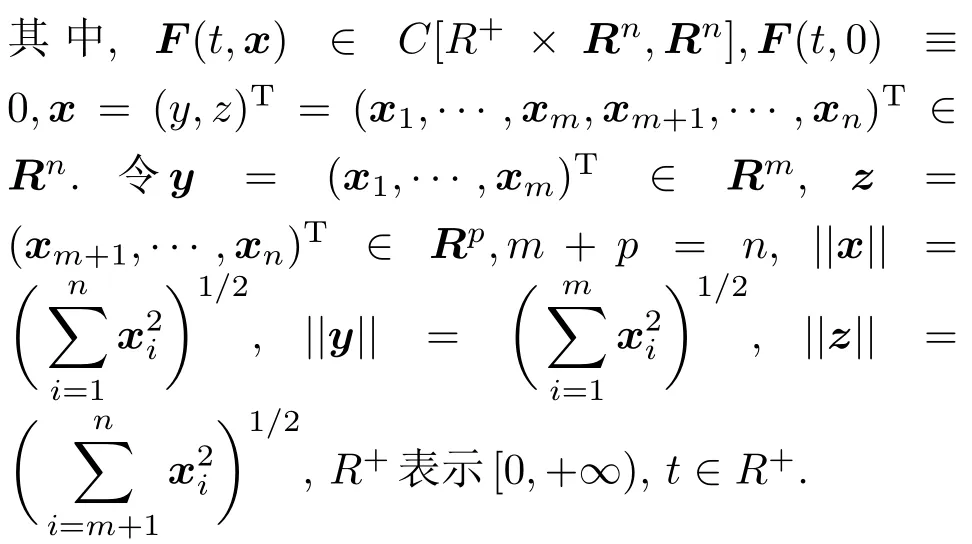
定義1[19]稱(1)式的平凡解關于部分變元y是穩定的,若?ε＞ 0,?t0∈ R+,?δ(t0,ε)＞0,?x0∈Sδ(n)={x|||x||＜δ},有

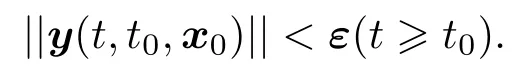
定義2[19]稱(1)式的平凡解關于部分變元y是吸引的,若?t0∈R+,?σ(t0)＞0,?ε＞0,?x0∈Sδ(t0)={x|||x||≤ σ(t0)},?T(t0,x0,ε)＞ 0,當t≥t0+T時,有

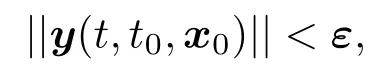
其中Sσ(t0)稱為關于y的吸引區域.

定義3[19]稱(1)式的平凡解關于部分變元y漸近穩定,若它關于y穩定且吸引.

定義4[19]若函數φ∈C[R+,R+](或C[(0,r), R+])是連續的嚴格單調上升函數,且有φ(0)=0,則稱φ屬于K類函數,記為φ∈K.

引理1[19]令?,ψ和α都是K類函數.若存在函數V(t,x)滿足

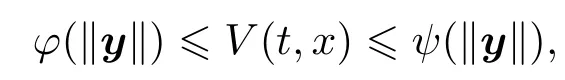
它的導數

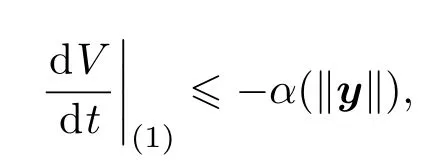
則(1)式的平凡解關于y漸近穩定.

接著,給出一個文中需要用到的有關矩陣的引理.

引理2 設H=(hij)∈RN×N,B=(bij)∈Rn×n,則存在nN階置換矩陣(即每一行和每一列都只有一個元素為1而其余元素均為0的方陣) P=Ps···P1,其中Pi是第一類初等行變換矩陣(即將單位矩陣的某兩行進行對換后的矩陣),使得等式成立.其中, i=1,···,s,s為正整數,為克羅內克積.

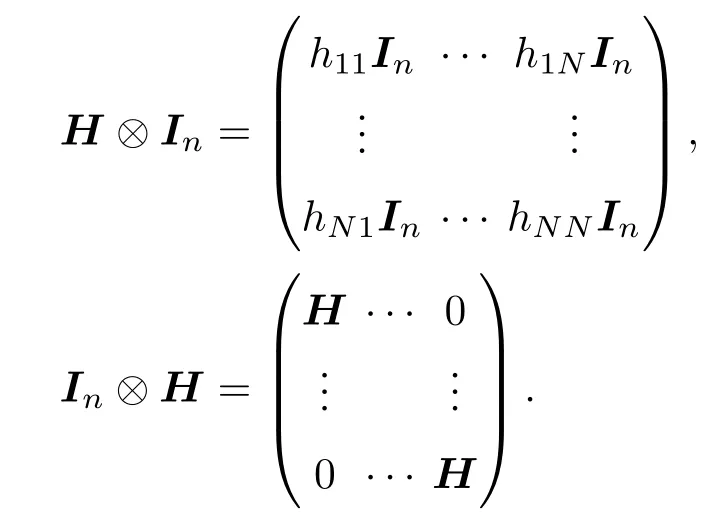
通過簡單計算可知,存在nN階置換矩陣P=Ps···P1,其中Pi是第一類初等行變換矩陣,使得.同理,

于是,

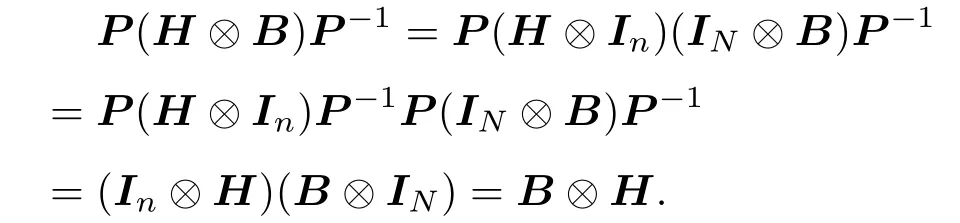
然后,介紹文中要用的圖論基礎知識.

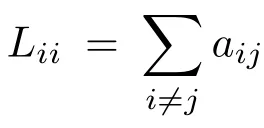
3 主要結果

本文將部分變元的穩定性理論運用到多智能體系統.考慮由N個智能體和一個領導者組成的一階多智能體系統,由文獻[13]的模型,可設每個跟隨智能體的動力學方程為

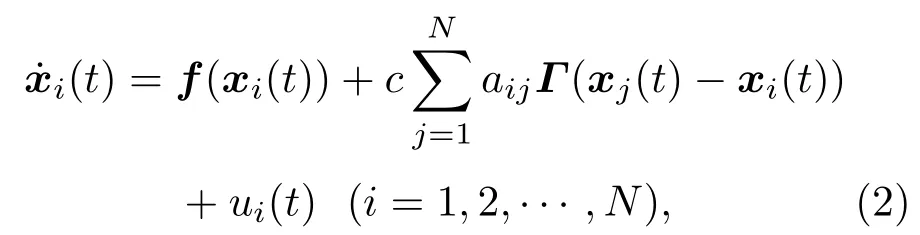
其中,xi=(xi1,···,xin)T∈Rn表示第i個智能體的狀態;f(xi)=(f1(xi),···,fn(xi))T是非線性連續函數;c＞ 0表示耦合強度;Γ = diag(r1,···,rn)∈Rn×n(rk≥0,k=1,···,n)表示內部耦合矩陣.

設領導智能體的狀態方程為

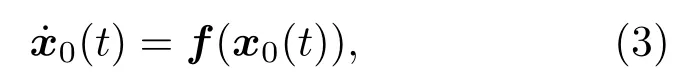
其中,x0=(x01,···,x0n)T∈Rn表示領導智能體的狀態,f(x0)=(f1(x0),···,fn(x0))T是非線性連續函數.

考慮有向網絡拓撲下的領導-跟隨多智能體系統部分分量一致性問題.類似于文獻[15]中的一致性協議,設計牽引控制器

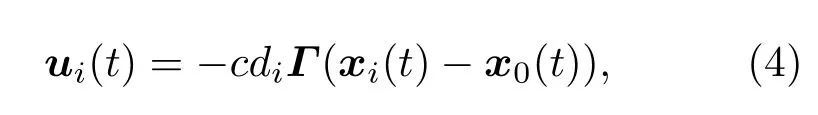
其中,c和Γ的意義與(2)式中的相同.當第i個智能體能接收到領導者的信息時,di＞0,否則di=0.

令ei(t)=xi(t)?x0(t).由(2),(3)和(4)式可以得到誤差系統

上式可以寫成向量形式

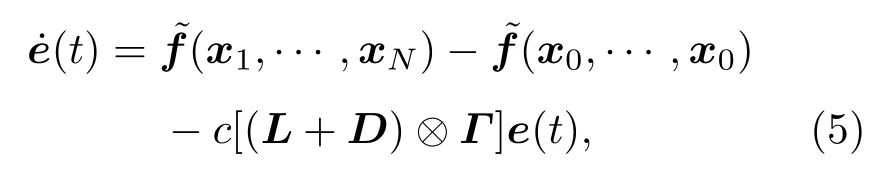
其中,

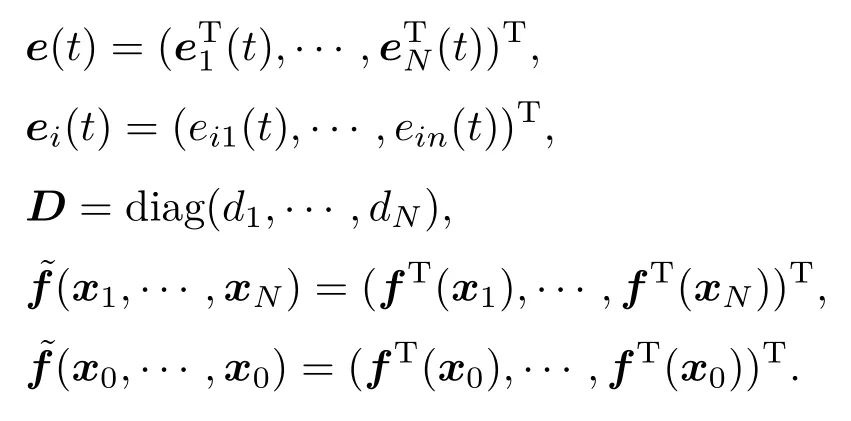
為了研究誤差系統(5)的平凡解關于部分變元的漸近穩定性,我們做如下變換:令= P e(t),其中P是引理2中的置換矩陣.令εk(t)= (e1k(t),···,eNk(t))T,k=1,···,n,通過計算可得因此,(5)式可以轉化為

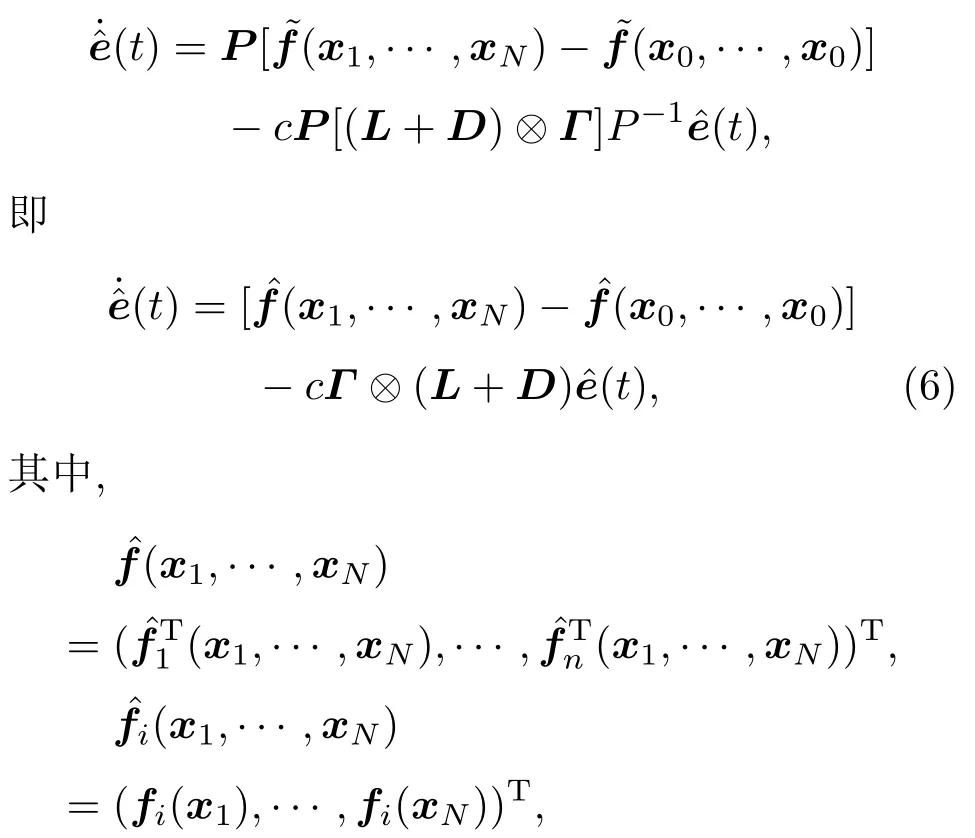
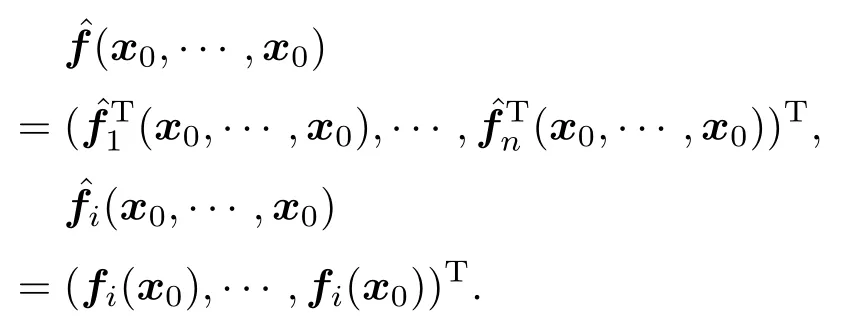
首先給出文中要用到的一個假設條件.

注: 與利普希茨條件相比,假設1的條件是弱化的條件.

然后,給出文中要用到的一個定義.

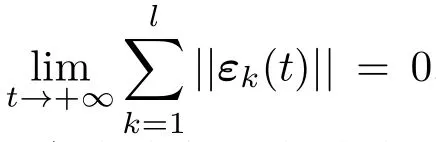
明顯地,若l=n,則定義5中的一致性就是通常意義下的一致性.這就是說,部分分量一致性是一種更一般化的群體動力學行為.

定理1 有向網絡拓撲結構下,對于控制項(4),若系統(2)和(3)滿足假設1,且滿足條件

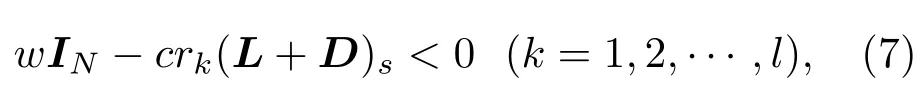
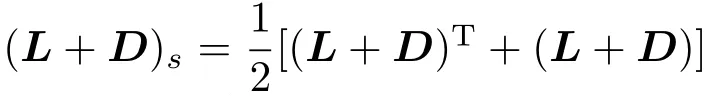
令

注1: 控制器(4)是牽引控制器.當網絡拓撲為平衡圖[7](即滿足條件:任何一個節點的入度等于出度,也就是L的行和與列和都等于0;無向圖是平衡圖的特例)時,只需牽制根節點就可以保證(L+D)s正定,故當c充分大時定理的條件可以成立.這就是說,對于平衡圖,只需牽制控制根節點即可.

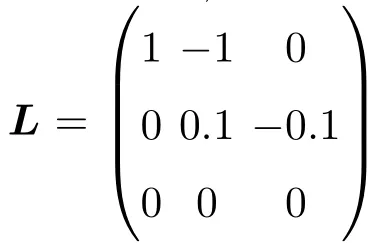
4 數值模擬

本節通過例子表明上一節中部分分量一致性理論結果的有效性.

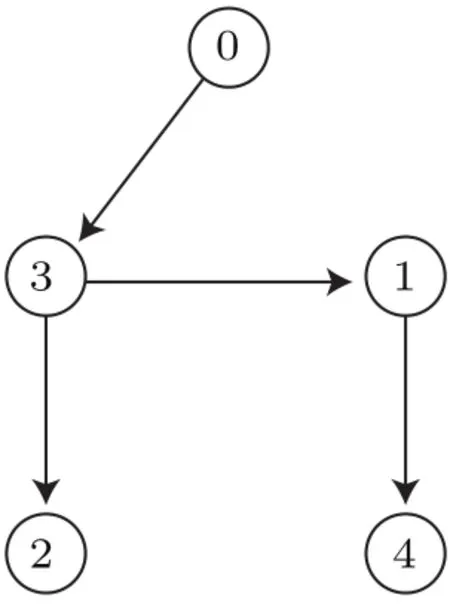
圖1 智能體連接的拓撲圖Fig.1.The ad jacent topology graph of agents.

例 令系統(2)中的N=4,n=3(圖1).下面我們考慮多智能體系統關于前兩個分量的一致性問題(即l=2).設領導智能體狀態的下標用0表示.令第i個智能體的狀態方程為

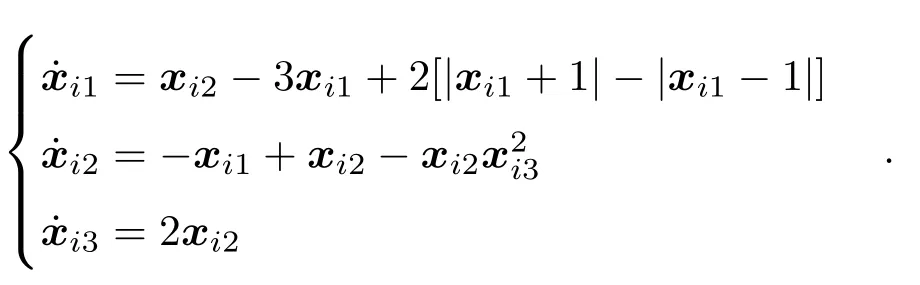
通過簡單計算,取w=1時假設1成立.取L和D分別為

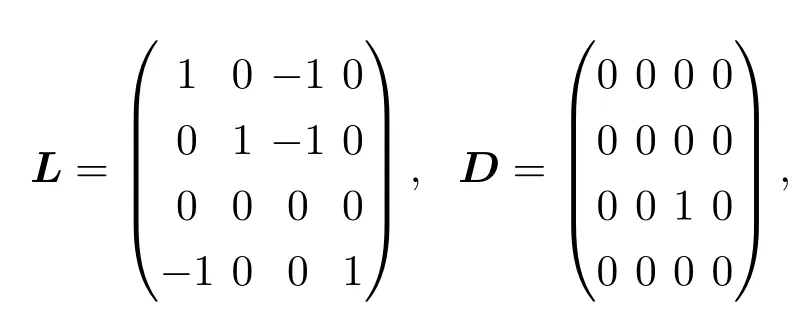
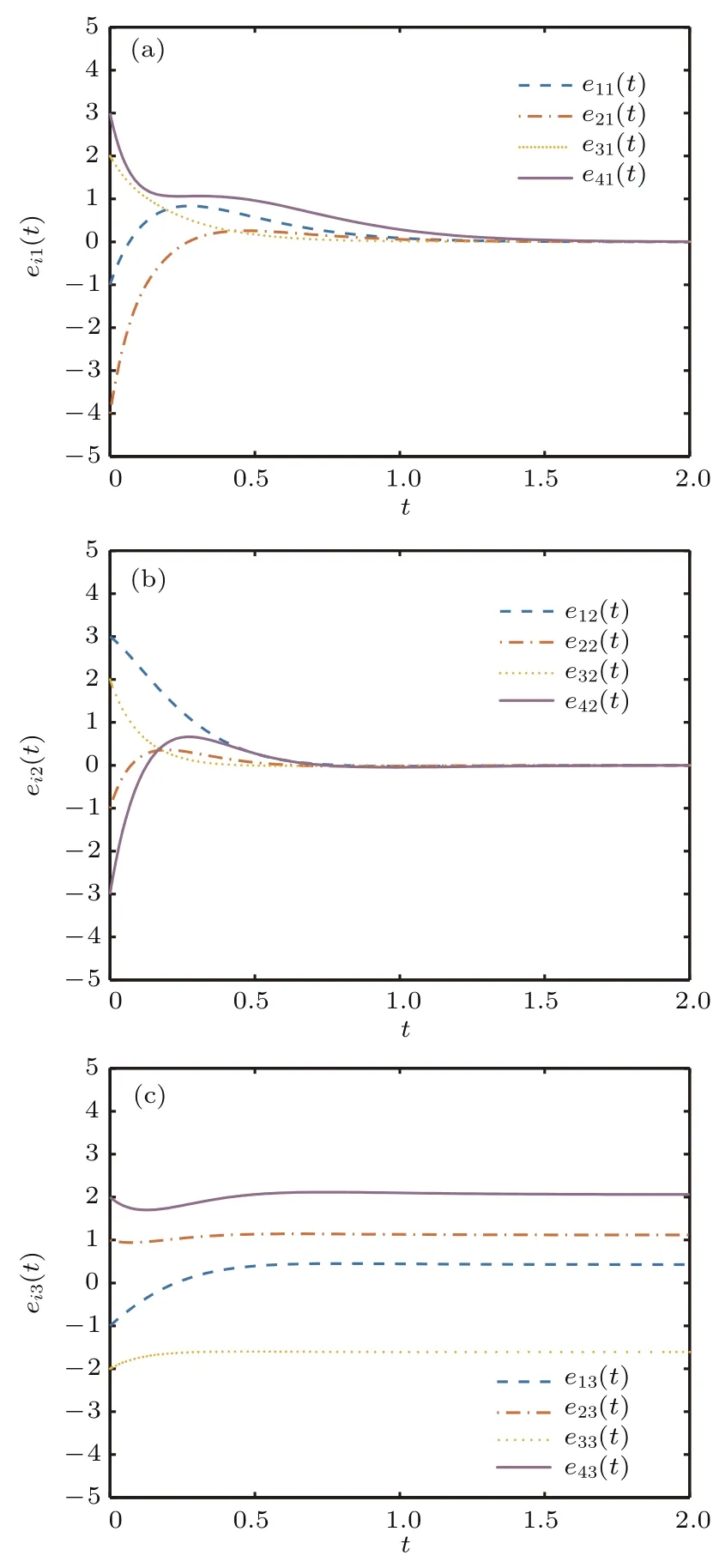
圖2 (網刊彩色)跟隨者與領導者的狀態誤差演化Fig.2.(color on line)The tim e evolution of the state errors between the leader and the followers.

則(L+D)s的最小特征值為λmin=0.1910.取Γ =diag(1,1,0)與c=6,不等式(7)成立.運用M atlab軟件計算,得到誤差軌跡如圖2所示.圖2(a)與圖2(b)表明了在牽制根節點(第3個節點)時系統(2)和(3)中所有智能體的前兩個分量都能達到一致,而圖2(c)說明另一個分量沒有達到一致.這就是說,與通常意義下的一致性比較,部分分量一致性是一種較弱的群體動力學行為.

5 結 論

本文考慮了具有領導者的一階非線性多智能體系統的部分分量一致性,在有向網絡拓撲結構下,給出了一個有效的牽引控制器,獲得了該系統達成部分分量一致性的一個充分條件,并運用矩陣理論和穩定性理論證明了該充分條件的正確性.然而,現實中還有一些現象是關于速度的部分分量一致性的,這就需要對二階甚至是高階多智能體系統的一致性進行研究.下一步,我們將討論二階多智能體系統的多個分量一致性問題.

[1]V icsek T,Czirok A,Ben-Jacob E,Cohen I,Shochet O 1995 Phys.Rev.Lett.75 1226

[2]Jadbabaie A,Lin J,M orse A S 2003 IEEE Trans.Autom.Con trol 48 988

[3]Qu Z H,W ang J,Hu ll R A 2008 IEEE Trans.Au tom. Con trol 53 894

[4]Cortes J,Bu llo F 2005 SIAM J.Con trol Optim ization 44 1543

[5]W ang N,W u Z H,Peng L 2014 Chin.Phys.B 23 108901

[6]Fax JA,M urray R M 2004 IEEE Trans.Autom.Control 49 1465

[7]O lfati-Saber R,M urray R M 2004 IEEE Trans.Autom. Con trol 49 1520

[8]Guo L X,Hu M F,Hu A H,Xu Z Y 2014 Chin.Phys. B 23 050508

[9]Ji L H,Liao X F 2012 Acta Phys.Sin.61 150202(in Chinese)[紀良浩,廖曉峰2012物理學報61 150202]

[10]X ie D S,X ie J Q,Zhao H Y 2015 Proceedings of the 34th Chinese Con trol Conference Hangzhou,China, Ju ly 28–30,2015 p7529

[11]Yu W W,Chen G R,Cao M,K urths J 2010 Autom atica 46 1089

[12]X in Y M,Li Y X,Huang X,Cheng Z S 2015 Neurocomputing 159 84

[13]Yu W W,Chen G R,Cao M 2011 IEEE Trans.Autom. Control 56 1436

[14]Zhao Y,Li B,Qin JH,Gao H J,Karim iH R 2013 IEEE Trans.Cybernet.43 2157

[15]Saad i P T,M ardani M M,Shasadeghi M,Safarinezhad ian B 2015 4th Iranian Join t Congress on Fuzzy and In telligen t System s Zahedan,Iran,Sep tem ber 9–11, 2015 p1

[16]N iW,Cheng D Z 2010 System Con trol Lett.59 209

[17]X ie Y Y,Wang Y,M a Z J 2014 Acta Phys.Sin.63 040202(in Chinese)[謝媛艷,王毅,馬忠軍2014物理學報63 040202]

[18]X iao F,Wang L,Chen J 2010 System Contro l Lett.59 775

[19]Liao X X 2001 M athem atica l Theory of Stability and Its Application(W uhan:Central China Norm al University Press)pp19,321,336(in Chinese)[廖曉昕2001穩定性的數學理論及應用(武漢:華中師范大學出版社)第19,321, 336頁]

PACS:02.30.Yy,02.30.Ks,05.65.+bDOI:10.7498/aps.66.060201

Partial com ponen t consensus o f leader-follow ing m u lti-agent system s?

Wu Bin-Bin1)2)Ma Zhong-Jun1)2)?Wang Yi3)

1)(School ofM athem atics and Com puting Science,Guilin University of Electronic Technology,Guilin 541004,China)
2)(Guangxi Colleges and Universities K ey Laboratory of Data Analysis and Com pu tation,Guilin University of E lectronic Technology,Guilin 541004,China)
3)(School ofM athem atics and Statistics,Zhejiang University of Finance and Econom ics,Hangzhou 310012,China)
(Received 29 June 2016;revised m anuscrip t received 30 Novem ber 2016)

Consensus prob lem s,as basic topics in distributed coordination ofmulti-agent system s,have d rawn a great deal of attention from diff erent research fields.Generally,consensus refers to the asym ptotic convergence of state variables of all agentsw ith tim e evolution.In this paper,a concep t on partial com ponent consensus in multi-agent system is fi rst given, which is a weaker dynam ic behavior of group than the consensus in general,and then the problem of partial com ponent consensus in leader-follow ing fi rst-ordermulti-agent system w ith the directed network topology is discussed.By designing an approp riate pinning control protocol and building corresponding error system,partial com ponent consensus in mu ltiagent system is transformed into the partial variable stability of the error system.Using matrix theory and stability theory,a suffi cient condition is given to realize partial com ponent consensus inmulti-agent system.Numericalsimu lations are given to illustrate the theoretical resu lts.

multi-agent system,consensus,partial component consensus

10.7498/aps.66.060201

?國家自然科學基金(批準號:11562006,61663006)、廣西自然科學基金(批準號:2015GXNSFAA 139013)、桂林電子科技大學研究生教育創新計劃(批準號:YJCXS201555)、廣西優秀中青年骨干教師培養工程項目(批準號:gxqg022014025)和浙江省自然科學基金(批準號:LY 17A 020007)資助的課題.

?通信作者.E-m ail:m zj1234402@163.com

*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.11562006,61663006),the Natu ral Science Foundation of Guangxi,China(G rant No.2015GXNSFAA 139013),the Innovation Pro ject of GUET G raduate Education,China(G rant No.YJCXS201555),the Outstanding Young Teachers Training in H igher Education Institutions of Guangxi,China(G rant No.gxqg022014025),and the Zhejiang Provincial Natural Science Foundation of China(Grant No.LY 17A 020007).

?Corresponding author.E-m ail:m zj1234402@163.com