強(qiáng)迫Lorenz系統(tǒng)的可預(yù)報性研究?
李保生1)2) 丁瑞強(qiáng)1)3)? 李建平4)5) 鐘權(quán)加1)2)
1)(中國科學(xué)院大氣物理研究所,大氣科學(xué)和地球流體力學(xué)數(shù)值模擬國家重點實驗室,北京 100029)
2)(中國科學(xué)院大學(xué)地球科學(xué)學(xué)院,北京 100049)
3)(成都信息工程大學(xué),高原大氣與環(huán)境四川省重點實驗室,成都 610225)
4)(北京師范大學(xué)全球變化與地球系統(tǒng)科學(xué)研究院,北京 100875)
5)(全球變化研究協(xié)同創(chuàng)新中心,北京 100875)
(2016年11月11日收到;2016年12月15日收到修改稿)
強(qiáng)迫Lorenz系統(tǒng)的可預(yù)報性研究?
李保生1)2) 丁瑞強(qiáng)1)3)? 李建平4)5) 鐘權(quán)加1)2)
1)(中國科學(xué)院大氣物理研究所,大氣科學(xué)和地球流體力學(xué)數(shù)值模擬國家重點實驗室,北京 100029)
2)(中國科學(xué)院大學(xué)地球科學(xué)學(xué)院,北京 100049)
3)(成都信息工程大學(xué),高原大氣與環(huán)境四川省重點實驗室,成都 610225)
4)(北京師范大學(xué)全球變化與地球系統(tǒng)科學(xué)研究院,北京 100875)
5)(全球變化研究協(xié)同創(chuàng)新中心,北京 100875)
(2016年11月11日收到;2016年12月15日收到修改稿)
根據(jù)非線性局部Lyapunov指數(shù)方法,分別以常數(shù)強(qiáng)迫Lorenz系統(tǒng)和準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)為例,研究了在外強(qiáng)迫存在的條件下混沌系統(tǒng)可預(yù)報性的改變.結(jié)果表明:外強(qiáng)迫會影響混沌系統(tǒng)的可預(yù)報性,兩種不同類型的強(qiáng)迫Lorenz系統(tǒng)的可預(yù)報期限都隨著外強(qiáng)迫的增強(qiáng)而增加,但是大小相等方向相反的外強(qiáng)迫對系統(tǒng)可預(yù)報性的影響不同,其中正值強(qiáng)迫比負(fù)值強(qiáng)迫作用下的可預(yù)報期限更長,并且這種差異隨著強(qiáng)度的增加而增大;不同形式的外強(qiáng)迫對可預(yù)報性的影響也不同,常數(shù)強(qiáng)迫的影響主要體現(xiàn)在誤差增長的線性階段,準(zhǔn)周期強(qiáng)迫的影響除了線性階段還必須考慮到非線性階段;當(dāng)強(qiáng)度相等的常數(shù)強(qiáng)迫和準(zhǔn)周期強(qiáng)迫驅(qū)動Lorenz系統(tǒng)時,常數(shù)強(qiáng)迫作用下的系統(tǒng)可預(yù)報性更高.本文基于混沌理論模型的研究,對于實際大氣的可預(yù)報性研究具有一定的啟示意義.
非線性局部Lyapunov指數(shù),可預(yù)報性,外強(qiáng)迫,Lorenz系統(tǒng)
1 引 言
大氣是一個復(fù)雜的非線性系統(tǒng),具有內(nèi)在隨機(jī)性[1,2],因此其可預(yù)報時效有一定的范圍,超出范圍,預(yù)報將失去技巧.雖然混沌系統(tǒng)對初值十分敏感,但是系統(tǒng)的短期行為仍是可預(yù)測的[3?7].大氣系統(tǒng)存在可預(yù)報性是其固有屬性,確定和估計這種預(yù)報時效的長短,研究誤差增長和傳播規(guī)律等是可預(yù)報性理論研究的主要內(nèi)容,其中定量的估計可預(yù)報時效也是一個重要課題.當(dāng)前關(guān)于可預(yù)報性的研究工作中,丁瑞強(qiáng)和李建平[8?10]提出的非線性局部Lyapunov指數(shù)(NLLE)的方法,克服了傳統(tǒng)Lyapunov指數(shù)的局限,不做任何線性近似,考慮到非線性項對誤差增長的貢獻(xiàn),而且能夠定量地估計混沌系統(tǒng)的可預(yù)報期限,該方法已經(jīng)被應(yīng)用到實際天氣和氣候的可預(yù)報性研究中,并取得了很好的效果[11?18].
在可預(yù)報性問題的研究中,除了要考慮初值的不確定性,外強(qiáng)迫的影響也很重要[19].大量的研究結(jié)果表明,強(qiáng)迫項在真實大氣中是不可忽視的,例如在氣候研究中常關(guān)注海表溫度或海冰對環(huán)流的強(qiáng)迫作用[20?22],尤其是準(zhǔn)周期為3—7年的ENSO循環(huán)對全球氣候變化的貢獻(xiàn)[23?25].外強(qiáng)迫條件的變化和異常會影響大氣內(nèi)部的動力過程,從而影響天氣和氣候的可預(yù)報性.但在以往有關(guān)強(qiáng)迫項的研究中,較少的工作涉及外強(qiáng)迫影響混沌系統(tǒng)可預(yù)報性的問題.外強(qiáng)迫的改變會使得混沌系統(tǒng)的可預(yù)報期限產(chǎn)生怎樣的變化,尚需進(jìn)一步的研究.同時,大氣作為非線性動力系統(tǒng),常用非線性理論模型來體現(xiàn)大氣系統(tǒng)運動的非周期性和運動軌跡對初值的敏感性,但以往的研究主要集中探討其動力結(jié)構(gòu)和動力學(xué)統(tǒng)計性質(zhì)等內(nèi)容[26,27],涉及可預(yù)報性方面的研究工作還較少.
本文借助于Lorenz理論模型,并利用NLLE的方法,給出了定常強(qiáng)迫Lorenz模型[28]和準(zhǔn)周期強(qiáng)迫Lorenz模型[29]在外強(qiáng)迫強(qiáng)度改變的條件下混沌系統(tǒng)誤差增長規(guī)律和可預(yù)報期限的變化,以及外強(qiáng)迫對Lorenz系統(tǒng)混沌性質(zhì)的影響.
2 方 法
本文采用NLLE方法定量地估計混沌系統(tǒng)的可預(yù)報期限.由于傳統(tǒng)的Lyapunov方法[30?32]都假設(shè)初始誤差無限小,誤差發(fā)展?jié)M足切線性近似,因而忽略了非線性項對誤差增長的貢獻(xiàn),使得傳統(tǒng)方法無法描述有限尺度大小的初始誤差對可預(yù)報性的貢獻(xiàn),因此存在很大的缺陷和不足.NLLE方法不做任何線性近似,保留所有的非線性項,直接對誤差演化的非線性方程進(jìn)行積分求解.
對于一個n維非線性動力系統(tǒng),其原始誤差演化方程表示如下:
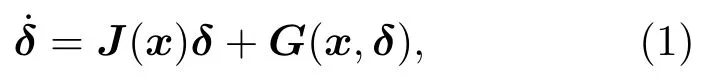
其中x是t時刻系統(tǒng)的狀態(tài)向量,δ是狀態(tài)x上疊加的誤差,J(x)δ是切線性項,G(x,δ)是關(guān)于誤差的高階非線性項.將誤差演化方程(1)的解從t=t0到t0+τ進(jìn)行數(shù)值積分,得到
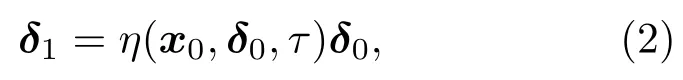
其中δ1= δ(t0+τ),x0=x(t0),δ0= δ(t0), η(x0,δ0,τ)為非線性誤差傳播算子. NLLE被定義為
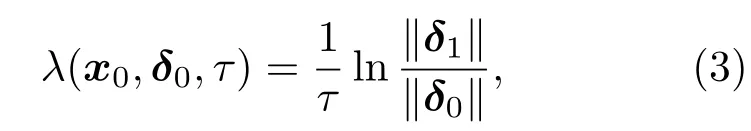
這里λ(x0,δ0,τ)不僅依賴于相空間中參考軌道的初始狀態(tài)x0和演化時間τ,還與初始誤差δ0有關(guān).系統(tǒng)全局吸引子上的整體集合平均的非線性局部Lyapunov指數(shù)可表示為

這里?代表系統(tǒng)全局吸引子的區(qū)域范圍,〈·〉N表示N(N→∞)個樣本的集合平均.在此基礎(chǔ)上可以獲得初始誤差的平均相對增長,

由(3),(4)和(5)式可得
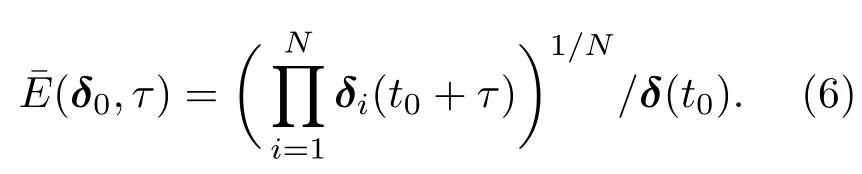
對于一個混沌系統(tǒng),隨著τ→ ∞,δ1(t0+τ), δ2(t0+τ),···,δN(t0+τ)相互獨立,并且收斂到同一分布,根據(jù)Ding和Li[8]證明的飽和定理,誤差的平均相對增長以概率意義收斂到一個常數(shù),即
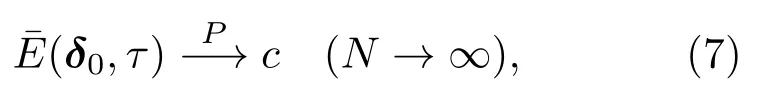
3 試驗設(shè)計
本文選取兩個簡單的強(qiáng)迫Lorenz系統(tǒng)來研究不同類型的強(qiáng)迫以及外強(qiáng)迫強(qiáng)度的改變對其可預(yù)報性的影響.
3.1 常數(shù)強(qiáng)迫Lorenz系統(tǒng)
在經(jīng)典Lorenz模型基礎(chǔ)上,Palmer[28]引入常數(shù)強(qiáng)迫的Lorenz模型,其方程為
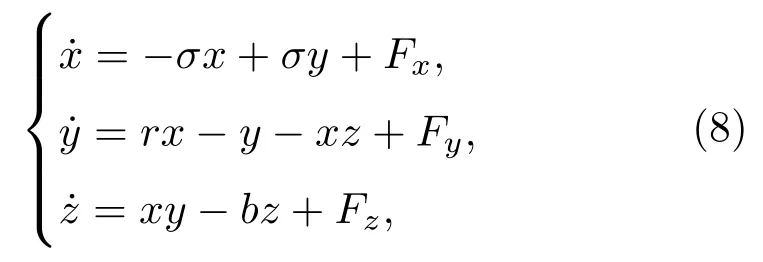
其中σ=10,r=28,b=8/3,分別為Prandtl數(shù)、Rayleigh數(shù)以及表示與對流尺度相聯(lián)系的參數(shù).強(qiáng)迫參量的選取,利用M ittal等[33]研究的情形,其中Fx=σF,Fy=?F,Fz=0.當(dāng)強(qiáng)迫項存在時, Lorenz系統(tǒng)出現(xiàn)混沌現(xiàn)象除了與自身參數(shù)σ,r,b有關(guān),還受到F的限制.這種條件下,強(qiáng)迫項存在臨界值Fc=1.61,僅當(dāng)|F|<Fc時,系統(tǒng)表現(xiàn)出混沌.本文在保證系統(tǒng)混沌性的前提下,通過變化強(qiáng)迫項F的大小來研究系統(tǒng)可預(yù)報性的改變.
3.2 準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)
本文選取的準(zhǔn)周期外力強(qiáng)迫的Lorenz方程如下:

方程中的參數(shù)σ,r,b與常數(shù)強(qiáng)迫情形下相同,A為準(zhǔn)周期外強(qiáng)迫的振幅;v為常數(shù),v=2π;w為無理數(shù),取值為,計算中采用有理數(shù)來近似表示,w=0.618.本文通過變化外強(qiáng)迫振幅A的大小來研究Lorenz系統(tǒng)的可預(yù)報期限對外力強(qiáng)迫的響應(yīng).
由于強(qiáng)迫Lorenz系統(tǒng)的控制方程已知,我們采用直接積分誤差演化方程的方法來計算NLLE,從而定量地確定不同強(qiáng)迫條件與系統(tǒng)可預(yù)報性的關(guān)系.
4 結(jié)果分析
4.1 常數(shù)強(qiáng)迫Lorenz系統(tǒng)
圖1給出了常數(shù)強(qiáng)迫Lorenz系統(tǒng)分別在有強(qiáng)迫和無強(qiáng)迫的條件下,初始誤差(δ0=10?6,下文同)的增長規(guī)律和可預(yù)報期限的變化情況.從圖1(a)可以看出:無論是否存在強(qiáng)迫,Lorenz系統(tǒng)的ˉλ都在最初階段表現(xiàn)出突然增加為較大的正值,這段時間可以認(rèn)為是初始誤差隨時間調(diào)整到誤差最快增長方向的適應(yīng)階段;隨后ˉλ逐漸趨于常數(shù),該階段為誤差增長的線性階段,誤差增長率在此階段表現(xiàn)出明顯的分離現(xiàn)象,其中有常數(shù)強(qiáng)迫條件下的ˉλ相比無強(qiáng)迫時的情形下要小;當(dāng)進(jìn)一步發(fā)展到非線性階段后,有強(qiáng)迫和無強(qiáng)迫系統(tǒng)的誤差增長率逐漸趨于一致.與之對應(yīng)的有強(qiáng)迫存在的情形下,lnˉE的增長也更為緩慢;盡管進(jìn)入到非線性階段后,最終達(dá)到的飽和值相等,但是有強(qiáng)迫存在時的lnˉE達(dá)到飽和需要的時間更長,即可預(yù)報期限增加(圖1(b)).以上結(jié)果表明,當(dāng)常數(shù)強(qiáng)迫存在時, Lorenz系統(tǒng)的誤差增長規(guī)律和可預(yù)報期限會發(fā)生改變.常數(shù)強(qiáng)迫的驅(qū)動使得系統(tǒng)的誤差增長更加緩慢,造成可預(yù)報性的增加,同時外強(qiáng)迫對誤差增長的影響主要體現(xiàn)在線性階段.
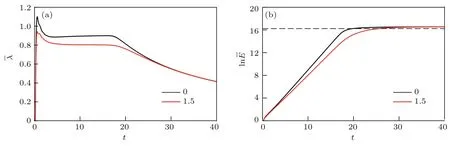
圖1 (網(wǎng)刊彩色)常數(shù)強(qiáng)迫Lorenz系統(tǒng)的(a)NLLE和(b)誤差的自然對數(shù)lnˉE隨t的變化(黑色實線,F=0;紅色實線,F=1.5;黑色水平虛線,飽和值的98%)Fig.1.(color on line)Tem poral evolution of(a)the NLLE and(b)the error grow th of the Lorenz system w ith constant forcing(b lack solid cu rves,F=0;red solid curves,F=1.5;b lack dashed horizontal cu rve m eans the value correspond ing to the 98%satu rated bias).
為了進(jìn)一步分析不同大小和方向的常數(shù)強(qiáng)迫對Lorenz系統(tǒng)的影響規(guī)律,圖2給出了Lorenz系統(tǒng)的誤差增長率和誤差增長曲線隨著不同常數(shù)強(qiáng)迫的變化.從圖2(a)可以看出:ˉλ在最開始經(jīng)過短時的調(diào)整之后,進(jìn)入到線性階段,在該階段表現(xiàn)出明顯的分離現(xiàn)象,隨著|F|的增大,線性階段的ˉλ隨之減小;當(dāng)發(fā)展到非線性階段之后,不同強(qiáng)迫條件下的誤差增長率趨于一致.誤差增長曲線(圖2(b))也顯示了相應(yīng)的發(fā)展情況,雖然混沌系統(tǒng)的初值誤差在各強(qiáng)迫條件下達(dá)到的飽和值相等,但是lnˉE的增長速度并不相同,|F|越大,增長曲線的曲率越大,意味著最終達(dá)到飽和所需的時間越長.此外,我們還可以注意到,大小相等方向相反的外強(qiáng)迫對可預(yù)報期限影響不同.當(dāng)F=±0.5時,誤差增長曲線比較接近;隨著F增加到±1.0時,兩條誤差增長曲線在線性增長階段有較為明顯的分離,并且F=1.0的誤差增長速度更為緩慢;當(dāng)F進(jìn)一步擴(kuò)大到±1.5時,誤差增長曲線的分離表現(xiàn)更為明顯,其中F=1.5的增長速度更慢.可見,大小相同方向相反的常數(shù)強(qiáng)迫并不都對誤差增長產(chǎn)生相同的影響,正值強(qiáng)迫對于可預(yù)報性增加的影響更為顯著.

圖2 (網(wǎng)刊彩色)不同強(qiáng)迫條件下,常數(shù)強(qiáng)迫Lorenz系統(tǒng)的(a)NLLE和(b)誤差的自然對數(shù)lnˉE隨t的變化(黑色水平虛線:飽和值的98%)Fig.2.(color on line)Tem poral evolution of(a)the NLLE and(b)the error grow th of the Lorenz system w ith d iff erent constant forcings(b lack dashed horizontal curve m eans the value corresponding to the 98% satu rated bias).
為了更加直觀地分析不同強(qiáng)迫對Lorenz系統(tǒng)可預(yù)報期限的影響,圖3給出了可預(yù)報性期限TP隨不同強(qiáng)度的常數(shù)強(qiáng)迫的變化曲線.首先,從圖3可以看出,隨著外強(qiáng)迫強(qiáng)度的增強(qiáng),可預(yù)報性也隨之增加;其次,曲線的非對稱性更明顯地表述出大小相等、方向不同的|F|對混沌系統(tǒng)產(chǎn)生著不同的影響,也說明了Lorenz系統(tǒng)對正負(fù)強(qiáng)迫的響應(yīng)不同. Lorenz系統(tǒng)可預(yù)報性的增加對正值強(qiáng)迫的響應(yīng)要比負(fù)值強(qiáng)迫更加明顯,隨著強(qiáng)迫強(qiáng)度的增加,這種差異越為顯著.
傳統(tǒng)Lyapunov指數(shù)常用來表示混沌系統(tǒng)的改變,Ding和Li[18]在研究中曾指出線性階段的NLLE與傳統(tǒng)Lyapunov指數(shù)大致相等,因此本文利用誤差增長率在其線性平穩(wěn)階段的平均值ˉλL來估計系統(tǒng)的內(nèi)部變化.從圖4給出的誤差增長線性階段的平均值ˉλL隨外強(qiáng)迫的變化曲線可以看出,不存在常數(shù)強(qiáng)迫時的ˉλL最大.隨著正強(qiáng)迫值的增加,ˉλL隨之減小,負(fù)值亦然.但不同的是,強(qiáng)迫為正值時,ˉλL曲線的下降趨勢比強(qiáng)迫為負(fù)值時更加明顯,意味著正值強(qiáng)迫下ˉλL減小速度更快,與圖3中的結(jié)論相符合.由此可見,外強(qiáng)迫的存在改變了系統(tǒng)的誤差增長規(guī)律,強(qiáng)迫越強(qiáng),誤差增長越慢,可預(yù)報期限越長;同時,對于強(qiáng)度相等的外強(qiáng)迫,正值強(qiáng)迫比負(fù)值強(qiáng)迫下的可預(yù)報期限更長.
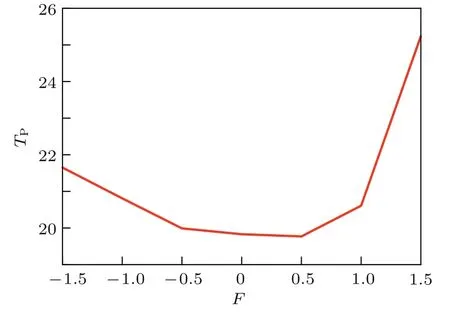
圖3 常數(shù)強(qiáng)迫Lorenz系統(tǒng)的可預(yù)報期限TP隨強(qiáng)迫F的變化Fig.3.The p redictability lim it TPof the Lorenz system w ith constant forcing variesw ith the ex ternal forcing strength F.
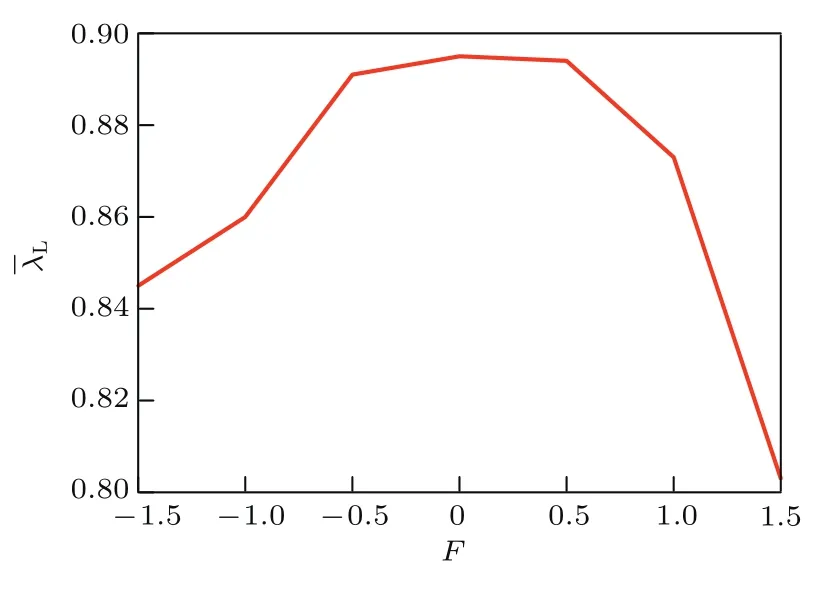
圖4 常數(shù)強(qiáng)迫Lorenz系統(tǒng)的ˉλL隨強(qiáng)迫F的變化Fig.4.The average NLLE of the linear phaseˉλLof the Lorenz system w ith constant forcing varies w ith the ex ternal forcing strength F.
4.2 準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)
圖5給出了Lorenz系統(tǒng)在準(zhǔn)周期強(qiáng)迫條件下的誤差增長率與誤差增長曲線.同常數(shù)強(qiáng)迫Lorenz系統(tǒng)一樣,系統(tǒng)誤差增長率在經(jīng)過短時間的調(diào)整后進(jìn)入到線性階段,此時系統(tǒng)受到準(zhǔn)周期強(qiáng)迫驅(qū)動的相比無強(qiáng)迫情形下的小,隨著時間發(fā)展,由于非線性作用的增強(qiáng),增長率最終趨于一致(圖5(a)).圖5(b)的誤差發(fā)展曲線也顯示出,系統(tǒng)存在準(zhǔn)周期外強(qiáng)迫時,初始誤差的增長速度要更加緩慢,達(dá)到飽和的時間更加長,可預(yù)報期限增加.由此可見,準(zhǔn)周期強(qiáng)迫增加了Lorenz系統(tǒng)的可預(yù)報性.

圖5 (網(wǎng)刊彩色)準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)的(a)NLLE和(b)誤差的自然對數(shù)lnˉE隨t的變化(黑色實線,A=0;紅色實線,A=15;黑色水平虛線,飽和值的98%)Fig.5.(color on line)Tem poral evolution of(a)the NLLE and(b)the error grow th of the Lorenz system w ith quasi-periodic forcing(b lack solid cu rves,A=0;red solid cu rves,A=15;b lack dashed horizontal curvem eans the value correspond ing to the 98%satu rated bias).
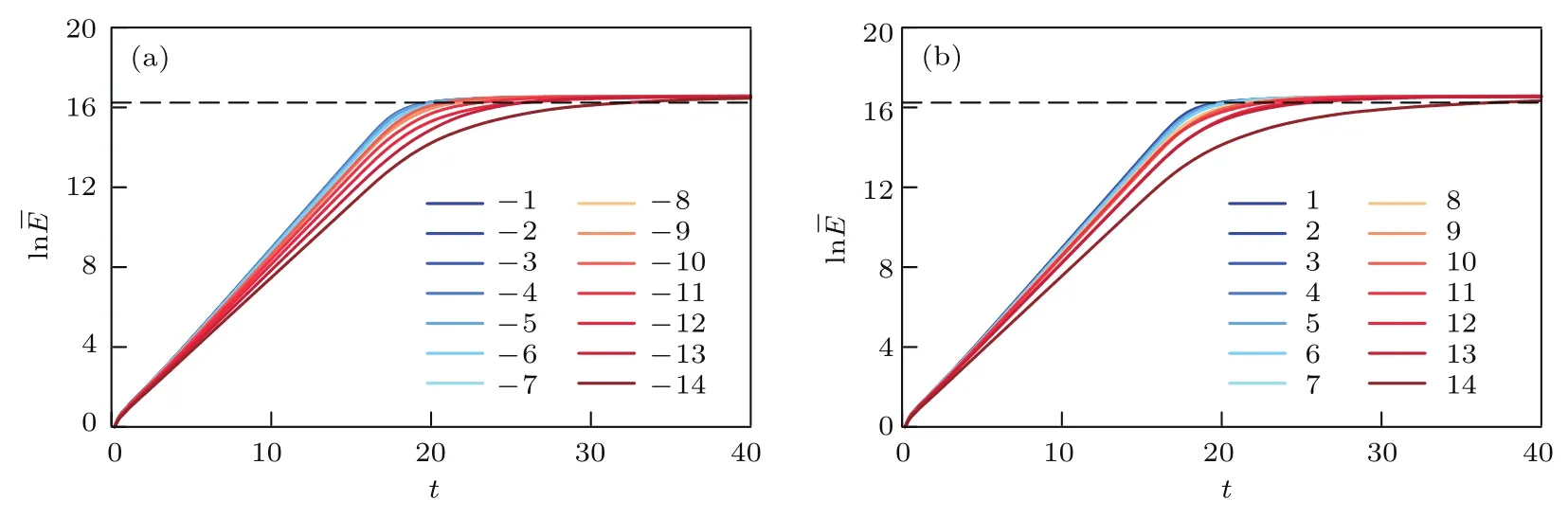
圖6 (網(wǎng)刊彩色)不同強(qiáng)迫條件下準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)的誤差自然對數(shù)lnˉE隨t的變化(黑色水平虛線:飽和值的98%) (a)準(zhǔn)周期強(qiáng)迫振幅A為負(fù)值;(b)準(zhǔn)周期強(qiáng)迫振幅A為正值Fig.6.(color on line)Tem poral evolution of the error grow th of the Lorenz system w ith diff erent quasiperiodic forcings(b lack dashed horizontal cu rvesm ean the value corresponding to the 98%saturated bias): (a)The quasi-period ic forcings are negative;(b)the quasi-periodic forcings are positive.
圖6給出的準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)在不同強(qiáng)迫振幅A作用下的誤差增長曲線,可以從中進(jìn)一步分析系統(tǒng)可預(yù)報期限隨強(qiáng)迫振幅的變化情況.外強(qiáng)迫振幅為負(fù)值的變化過程中(圖6(a)),當(dāng)A在?9內(nèi)變動時,誤差增長達(dá)到飽和需要的時間有增加的趨勢,但是尚不明顯,比較接近無強(qiáng)迫條件下的情形;但當(dāng)A從?10開始增加,隨著|A|的增加,誤差增長速度減小趨勢顯著,達(dá)到飽和所需要的時間也明顯增加;外強(qiáng)迫為較小的正值時(圖6(b)),誤差增長同樣比較接近無強(qiáng)迫的情形;當(dāng)A從7開始增加,可以看出誤差增長曲線的曲率依此增大,即誤差增長速度依此減小,達(dá)到飽和的時間增加.以上結(jié)果表明,在不考慮外強(qiáng)迫方向的前提下,初始誤差的增長速度在整體上表現(xiàn)出隨著外強(qiáng)迫振幅的增加而減小,從而使得可預(yù)報期限增加.
圖7給出了準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)的可預(yù)報期限在不同的振幅作用下的變化曲線.從圖7可以更明顯地看出,在A=0時的可預(yù)報期限最短,隨著|A|的增加,可預(yù)報期限增加,這一趨勢隨著外強(qiáng)迫的增強(qiáng)變的明顯;在|A|較小時,TP的增長過程存在一定的波動,這與圖6分析的誤差增長曲線分離不明顯結(jié)果對應(yīng);可預(yù)報期限變化曲線的非對稱性表明,大小相等方向不同的外強(qiáng)迫對系統(tǒng)可預(yù)報性的影響效果不同,當(dāng)外強(qiáng)迫的振幅較小時,外強(qiáng)迫方向的影響尚不顯著,但是當(dāng)振幅較大時,外強(qiáng)迫方向的作用使得正值強(qiáng)迫驅(qū)動下的系統(tǒng)可預(yù)報期限更長.
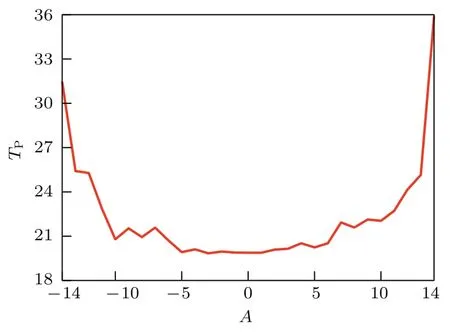
圖7 準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)的可預(yù)報期限TP隨強(qiáng)迫振幅A的變化Fig.7.The p redictability lim it TPof the Lorenz system w ith quasi-periodic forcing varies w ith the ex ternal forcing m agnitude A.
圖8給出了準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)的NLLE在線性平穩(wěn)階段的平均值ˉλL隨強(qiáng)迫振幅A的變化曲線.首先,隨著|A|的增加,ˉλL呈現(xiàn)減小趨勢,即系統(tǒng)誤差增長速度依此減緩,圖7得出的可預(yù)報性增加的結(jié)論與之對應(yīng);其次,ˉλL在減小的過程中存在波動,尤其當(dāng)|A|較小時表現(xiàn)明顯,解釋了可預(yù)報期限的波動增加趨勢;圖8中大小相等的外強(qiáng)迫,負(fù)值時的ˉλL比正值時的小,這時負(fù)值下的可預(yù)報期限應(yīng)該更大,但圖7中的結(jié)果顯示正值時較大.這可能是因為隨著外強(qiáng)迫的增強(qiáng),準(zhǔn)周期強(qiáng)迫對于非線性階段的影響開始顯著,不再局限于誤差增長的線性階段,這是與常數(shù)強(qiáng)迫不同的地方,即不同形式的外強(qiáng)迫對系統(tǒng)誤差增長的影響階段是不同的.
為進(jìn)一步說明不同形式的外強(qiáng)迫對系統(tǒng)誤差增長的影響不同,圖9給出了外強(qiáng)迫的強(qiáng)度相等(外強(qiáng)迫強(qiáng)度都選取為?1)時,常數(shù)強(qiáng)迫Lorenz系統(tǒng)和準(zhǔn)周期外強(qiáng)迫Lorenz系統(tǒng)的誤差增長率和誤差增長曲線.從圖9可以看出,常數(shù)強(qiáng)迫情形下的誤差增長在其線性階段更加緩慢,最終達(dá)到飽和的時間更久,可預(yù)報期限更長.這種結(jié)果顯示出,強(qiáng)度相等形式不同的外強(qiáng)迫對系統(tǒng)的影響是不同的,系統(tǒng)受到常數(shù)強(qiáng)迫影響的可預(yù)報期限更長,因此當(dāng)我們考慮外強(qiáng)迫對可預(yù)報性的影響時,也應(yīng)該考慮到外強(qiáng)迫的不同形式.
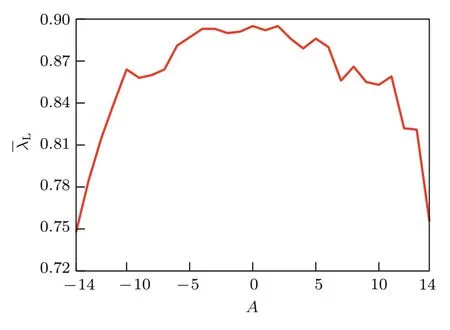
圖8 準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng)的ˉλL隨強(qiáng)迫振幅A的變化Fig.8.The average NLLE of the linear phaseˉλLof the Lorenz system w ith quasi-periodic forcing variesw ith the external forcing m agnitude A.
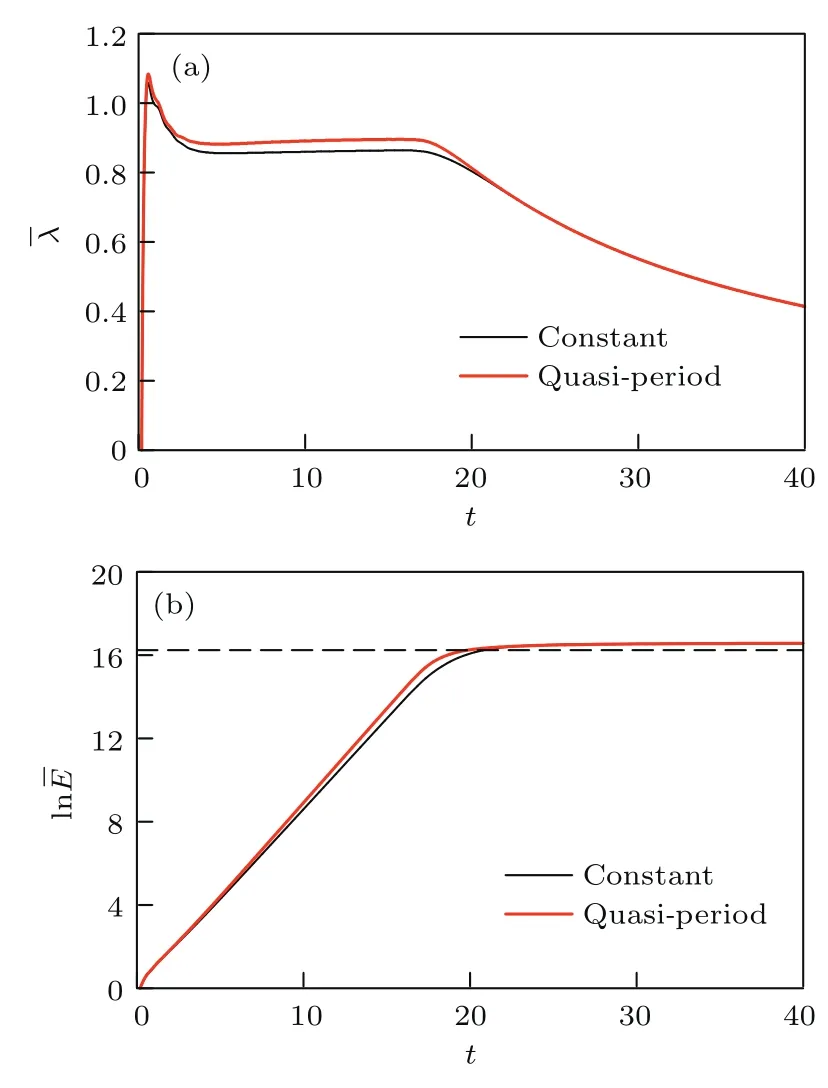
圖9 (網(wǎng)刊彩色)不同強(qiáng)迫Lorenz系統(tǒng)的(a)NLLE和(b)誤差的自然對數(shù)隨t的變化(黑色實線,準(zhǔn)周期強(qiáng)迫Lorenz系統(tǒng);紅色實線,常數(shù)強(qiáng)迫Lorenz系統(tǒng);黑色水平虛線,飽和值的98%)Fig.9.(color on line)Tem poral evolution of(a)the NLLE and(b)the error grow th of the d iff erent forced Lorenz system(b lack solid cu rves,the Lorenz system w ith constant forcing;red solid curves,the Lorenz system w ith quasi-period ic forcing;b lack dashed horizontal curve m eans the value corresponding to the 98% satu rated bias).
5 討論與結(jié)論
本文基于兩個不同類型的強(qiáng)迫Lorenz理論模型,利用NLLE方法考察了在外強(qiáng)迫改變的情況下混沌系統(tǒng)的可預(yù)報性問題,主要研究結(jié)論如下.
1)外強(qiáng)迫會對系統(tǒng)的可預(yù)報性產(chǎn)生影響.兩種不同強(qiáng)迫類型的系統(tǒng)可預(yù)報期限都隨著外強(qiáng)迫的增強(qiáng)而增加;大小相同方向不同的外強(qiáng)迫作用不同,系統(tǒng)可預(yù)報性對正值強(qiáng)迫的響應(yīng)要比負(fù)值強(qiáng)迫更加明顯,系統(tǒng)在正值強(qiáng)迫作用下的誤差增長率更小,可預(yù)報期限更長,并且這種差異隨著強(qiáng)迫的增強(qiáng)而增加.
2)不同類型的外強(qiáng)迫對于系統(tǒng)誤差增長的影響不同.常數(shù)強(qiáng)迫的影響主要體現(xiàn)在誤差增長的線性階段;準(zhǔn)周期強(qiáng)迫作用下,隨著強(qiáng)迫的增加,誤差增長的非線性階段同樣受到影響;在外強(qiáng)迫強(qiáng)度相等時,混沌系統(tǒng)在常數(shù)強(qiáng)迫驅(qū)動下的可預(yù)報期限比準(zhǔn)周期強(qiáng)迫時更長.
本文雖然基于簡單的理論模型進(jìn)行研究,但是其結(jié)果對于實際天氣具有一定的啟示意義.首先,大氣可預(yù)報性的研究中,選取外強(qiáng)迫的強(qiáng)度對大氣可預(yù)報性有重要影響,外強(qiáng)迫增強(qiáng)會使得大氣可預(yù)報性增加,因此外強(qiáng)迫大小的選取在實際研究中要合理.其次,強(qiáng)迫的類型不同對于可預(yù)報性的影響不同,比如在大氣可預(yù)報性的研究工作中,經(jīng)常將海溫作為外強(qiáng)迫驅(qū)動大氣,但是選擇海溫作為常數(shù)外強(qiáng)迫或準(zhǔn)周期外強(qiáng)迫的不同情形下,大氣可預(yù)報性是不同的;此外,強(qiáng)度相等方向不同的強(qiáng)迫對于可預(yù)報性的作用效果不一致,這種非對稱性隨著外強(qiáng)迫的增強(qiáng)變得更加明顯,可能是由于非線性的作用使得正負(fù)強(qiáng)迫條件下的信號強(qiáng)度表現(xiàn)不同,但是關(guān)于系統(tǒng)內(nèi)部的動力行為仍有待深入研究.這對于實際研究同樣重要,過去研究中我們常將強(qiáng)迫項作為一個整體去考慮,然而大氣和海洋中存在著許多正負(fù)相反的氣象要素和位相不同的模態(tài),如海溫的正負(fù)異常、ENSO的正負(fù)位相等,由于方向不同的外力對于實際大氣或海洋的動力過程影響是不同的,所以應(yīng)該分別考慮不同位相驅(qū)動下的可預(yù)報性問題.總之,大氣和海洋的研究中存在著多種不同的準(zhǔn)周期強(qiáng)迫項和常數(shù)強(qiáng)迫項,探索實際可預(yù)報性仍需要進(jìn)一步的努力.
[1]Lorenz E N 1963 J.A tm os.Sci.20 130
[2]Chou J F 2002 Non linearity and Com plexit in A tm ospheric Sciences(Beijing:China M eteorological Press) p131(in Chinese)[丑紀(jì)范2002大氣科學(xué)中的非線性和復(fù)雜性(北京:氣象出版社)第131頁]
[3]Lorenz E N 1965 Tellus A 17 321
[4]Lorenz E N,Palm er T N,Hagedorn R 1995 Proceedings of a Sem inar Held at ECMW F on Predictability(I), 1995 p1
[5]Li J P,Chou J F 2003 Chin.J.Atm os.Sci.27 653(in Chinese)[李建平,丑紀(jì)范2003大氣科學(xué)27 653]
[6]Duan W S,M u M 2006 Chin.J.Atm os.Sci.30 759(in Chinese)[段晚鎖,穆穆2006大氣科學(xué)30 759]
[7]Duan W S,Ding R Q,Zhou F F 2013 C lim atic Environ. Res.18 524(in Chinese)[段晚鎖,丁瑞強(qiáng),周菲凡 2013氣候與環(huán)境研究18 524]
[8]D ing R Q,Li J P 2007 Phys.Lett.A 364 396
[9]Ding R Q,Li J P 2007 Chin.J.Atm os.Sci.31 571(in Chinese)[丁瑞強(qiáng),李建平2007大氣科學(xué)31 571]
[10]D ing R Q,Li J P 2008 Acta Phys.Sin.57 7494(in Chinese)[丁瑞強(qiáng),李建平2008物理學(xué)報57 7494]
[11]Li J P,D ing R Q 2008 Chin.J.A tm os.Sci.32 975(in Chinese)[李建平,丁瑞強(qiáng)2008大氣科學(xué)32 975]
[12]D ing R Q,Li J P 2009 Acta M eteor.Sin.67 343(in Chinese)[丁瑞強(qiáng),李建平2009氣象學(xué)報67 343]
[13]D ing R Q,Li J P,Seo K H 2010 M on.Wea.Rev.138 1004
[14]D ing R Q,Li J P,Seo K H 2011 M on.Wea.Rev.139 2421
[15]D ing R Q,Li J P 2011 M on.W ea.Rev.139 3265
[16]Ding R Q,Li J P 2013 Int.J.Clim atol.33 1936
[17]D ing R Q,Li J P,Zheng F,Feng J,Liu D Q 2015 C lim ate Dyn.46 1563
[18]Ding R Q,Li J P 2012 Adv.Atm os.Sci.29 1078
[19]Reich ler T J,Roads J O 2003 Non linear Proc.Geoph. 10 211
[20]Yang X Q,X ie Q,Huang T S 1992 Acta M eteor.Sin. 50 349(in Chinese)[楊修群,謝倩,黃士松1992氣象學(xué)報50 349]
[21]Li C Y,Zhu J H,Sun Z B 2002 Clim atic Environ.Res. 7 209(in Chinese)[李崇銀,朱錦紅,孫照渤2002氣候與環(huán)境研究7 209]
[22]LiW J,Li Y,Chen L J,Zhao Z G 2013 J.Appl.M eteor. Sci.24 385(in Chinese)[李維京,李怡,陳麗娟,趙振國2013應(yīng)用氣象學(xué)報24 385]
[23]Charles C D,Hunter D E,Fairbanks R G 1997 Science 277 925
[24]W ang B,W u R G,Fu X H 2000 J.C lim ate 13 1517
[25]Zhang Z S,Hu P,Feng G L 2016 Acta M eteor.Sin.74 165(in Chinese)[張志森,胡泊,封國林2016氣象學(xué)報74 165]
[26]Gong Z Q,Feng G L,Dong W J,Li J P 2006 Acta Phys. Sin.55 3180(in Chinese)[龔志強(qiáng),封國林,董文杰,李建平2006物理學(xué)報55 3180]
[27]Gong Z Q,Zhou L,Zhi R,Feng G L 2008 Acta Phys. Sin.57 5351(in Chinese)[龔志強(qiáng),周磊,支蓉,封國林2008物理學(xué)報57 5351]
[28]Palm er T N 1994 Proceedings-Indian National Science Academ y Part A 60 57
[29]He W P,Feng G L,Gao X Q 2006 Acta Phys.Sin.55 3175(in Chinese)[何文平,封國林,高新全2006物理學(xué)報55 3175]
[30]W olf A,Sw ift J B,Sw inney H L,Vastano J A 1985 Physica D 16 285
[31]Eckm ann J P,Ruelle D 1985 Rev.M od.Phys.57 617
[32]Lacarra J F,Talagrand O 1988 Tellus 40A 81
[33]M ittal A K,Dw ived i S,Pandey A C 2005 Non lin.Pro. Geophy.12 707
PACS:05.45.–a,92.60.WcDOI:10.7498/aps.66.060503
P red ictab ility of forced Lorenz system?
Li Bao-Sheng1)2)Ding Rui-Qiang1)3)?Li Jian-Ping4)5)Zhong Quan-Jia1)2)
1)(State Key Laboratory of Num erical M odeling for A tm ospheric Sciences and Geophysical F luid Dynam ics(LASG),Institu te of
A tm ospheric Physics,Chinese Academ y of Sciences,Beijing 100029,China)
2)(College of Earth Sciences,University of Chinese Academ y of Sciences,Beijing 100049,China)
3)(Plateau Atm osphere and Environm ent K ey Laboratory of Sichuan Province,Chengdu University of Inform ation Technology, Chengdu 610225,China)
4)(College ofG lobal Change and Earth System Science(GCESS),Beijing Norm al University,Beijing 100875,China)
5)(Joint Center for G lobal Change Studies,Beijing 100875,China)
(Received 11 Novem ber 2016;revised m anuscrip t received 15 Decem ber 2016)
In recent years,the actual atm ospheric p redictability has attracted w idespread attention.Im proving our understanding of weather p redictability is vital to developing num ericalm odels and im p roving our forecast skill in weather and climate events.Given that the atmosphere is a com p lex and non linear system,taking the Lorenz system as an exam p le is a better way to understand the actual atm osphere predictability.Up to now,som e p redictability p roblem s of the Lorenz system have been investigated,such as the relative eff ects of the initial error and themodel error.Previous advances in the research of predictability m ainly focus on the relationship between the predictability lim it and the initial error.As iswell known,the external forcing can also resu lt in the change of the predictability.Therefore,it is significant to investigate the predictability changing w ith the external forcing.The nonlinear local Lyapunov exponent(NLLE)is introduced to m easure the average grow th rate of the initial error of non linear dynam icalm odel,which has been used for quantitatively determ ining the predictability lim it of chaos system.Based on the NLLE app roach,the infl uences of external forcing on the p redictability are studied in the Lorenz system w ith constant forcing and Lorenz system w ith quasi-periodic forcing in this paper.The results indicate that for the Lorenz system s w ith constant and quasi-periodic forcings respectively,their predictability lim its increase w ith forcing strength increasing.In the case of the sam e m agnitude but diff erent directions,the constant and quasi-periodic forcing both show diff erent eff ects on the predictability lim it in the Lorenz system,and these eff ects becom e significant w ith the increase of forcing strength.Generally speaking, the positive forcing leads to a higher predictability lim it than the negative forcing.Therefore,when we consider the eff ects of positive and negative elem ents and phases in the atm osphere and ocean research,the p redictability problem s driven by diff erent phases should be considered separately.In addition,the infl uences of constant and quasi-periodic forcings on the p redictability are diff erent in the Lorenz system.The eff ect of the constant forcing on the predictability ism ainly refl ected in the linear phase of error grow th,while the non linear phase should also be considered additionally for the case of the quasi-periodic forcing.The p redictability of the system under constant forcing is higher than that of the system under quasi-periodic forcing.These resu lts based on sim p le chaoticmodel could provide an insight into the predictability studies of com p lex system s.
nonlinear local Lyapunov exponent,predictability,external forcing,Lorenz system
10.7498/aps.66.060503
?國家自然科學(xué)基金優(yōu)秀青年科學(xué)基金(批準(zhǔn)號:41522502)、“全球變化與海氣相互作用”專項(批準(zhǔn)號:GASI-IPOVA I-06)和國家重點研發(fā)計劃(批準(zhǔn)號:2016YFA 0601801)資助的課題.
?通信作者.E-m ail:d rq@m ail.iap.ac.cn
*Pro ject supported by the National Natural Science Foundation of China for Excellent Young Scholars(G rant No.41522502), the National Programm e on G lobalChange and A ir-Sea Interaction,China(G rant No.GASI-IPOVA I-06),and the National Key Research and Developm ent P lan of China(G rant No.2016YFA 0601801).
?Corresponding au thor.E-m ail:d rq@m ail.iap.ac.cn

