多層動態分簇的WSN時間同步算法*

杜永文,馮 珂,彭 沖

(蘭州交通大學電子與信息工程學院,蘭州 730070)

?

多層動態分簇的WSN時間同步算法*

杜永文*,馮 珂,彭 沖

(蘭州交通大學電子與信息工程學院,蘭州 730070)

無線傳感器網絡受多跳傳輸延遲和節點中的晶振準確度的影響,造成時間同步誤差較大。為了減小同步誤差,傳統解決方法提高了同步算法的頻率,這使得算法面臨兩個問題:①通信能耗較高;②精度與能耗之間的不平衡。針對以上問題,結合單向廣播機制和雙向成對機制,提出一種多層動態分簇的無線傳感器網絡時間同步算法。采用節點分層策略減少了同步通信開銷;采用同步誤差補償機制降低了算法同步誤差的影響,使用時鐘補償機制減少了傳感器節點運行的累積誤差。實驗測試表明:在保證精度的前提下,本算法降低了同步次數,減少了同步通信開銷,從而延長了網絡的生命周期。

無線傳感器網絡;時間同步;傳輸延遲;晶振

無線傳感器網絡WSN(Wireless Sensor Network)是一種分布式的自組織網絡,時間同步作為關鍵技術之一發揮著重要作用。傳感器網絡內部節點只有保持時間同步,才能互相協作完成相應的任務。數據融合、節點定位、休眠周期的同步、介質訪問控制(MAC)鏈路調度等都需要統一的時鐘基準。所以研究一種精準、高效的時間同步算法具有重要的科研意義和實用價值。

目前常用的無線傳感器網絡時間同步算法主要可分為2類:單向廣播同步和雙向成對同步。單向廣播時間同步算法采用單向報文進行時間同步,以參考廣播同步(RBS)[1]算法為例,該類算法在排除了發送端的不確定性后,它的到達時間被接收節點用作參考來對比本地時鐘,從而實現接收者彼此同步,但為提高單向報文的時間精度,往往需要提高報文發送頻率,這會致使同步報文發送過多,能耗較大。雙向成對時間同步算法采用雙向報文交換機制實現節點間的時間同步,以時間同步協議(TPSN)[2]算法為例,雙向報文可以較準確的估計無線傳輸延遲,但雙向報文使得時間同步報文交互數量增加,增大節點能耗,且同步時間存在累積誤差。除此之外,時間同步算法還有仿生時間同步算法,如螢火蟲同步算法[3]。螢火蟲同步算法要求每個傳感器節點安裝一個RC振蕩器(由電阻R和電容C構成的適用于產生低頻信號的電路),增大了傳感器節點的成本,增加了節點能耗,不利于大規模傳感器網絡的布置。

本文針對傳感器網絡能量的特點,提出了一種基于多層動態分簇的主次分級時間同步算法——PSLTS(Primary-Secondary Layered Time Synchronization)。PSLTS算法采用多層動態分簇的策略,將網絡節點劃分為主次兩層網絡,在簇首通信的主網絡中使用傳感器網絡TPSN的思想進行時間同步;簇內通信的次網絡在不降低時間精度的前提下降低簇首節點能量消耗,采用延遲測量時間同步(DMTS)算法的思想進行時間同步。同時采用同步誤差補償機制修正由于跳數距離增加造成的同步誤差,采用時鐘補償機制減少長時間工作由于晶振頻率不穩造成的誤差,從而提高時間同步精度。同TPSN算法以及ATSP算法比較,PSLTS算法降低了時鐘同步的頻率,降低能量消耗。

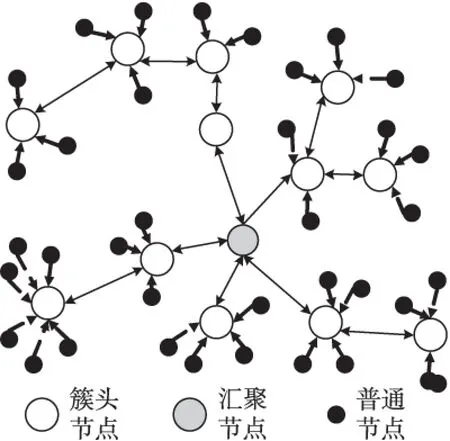
圖1 網絡拓撲結構

1 多層動態分簇的PSLTS算法

1.1 網絡拓撲結構

PSLTS算法采用動態分簇方式對網絡拓撲進行層次式劃分,將網絡節點劃分為主次兩種網絡。主網絡中簇首節點將數據融合后再采用多跳通信方式把數據傳送到匯聚節點,次網絡中同一簇的簇首節點和簇內成員節點通過單跳通信,進行信息匯聚[4]。基于動態分簇的無線傳感器網絡拓撲結構如圖1所示[5]。

1.2 主網絡-簇間通信網絡

圖1所示網絡的簇首節點形成了主網絡,其拓撲如圖2所示。

圖2 主網絡拓撲結構

采用多跳網絡的TPSN算法思想將主網絡時間同步分成兩個階段。①第1階段為層次發現階段[6],該階段在網絡分簇后將網絡簇首節點層次化,將匯聚節點作為第0層參考節點;根據簇首節點到匯聚節點的跳數分為1到n層;②第2階段為時鐘同步階段,層次結構建立后,通過時間同步包,從1層到n層逐層時鐘同步。

PSLTS算法中的簇首節點避免了TPSN中節點要與多個上層節點同步,而只與其直接父節點同步,減少了消息交換數目和同步時間。

主網絡簇間通信算法采用基于雙向報文的時間同步算法。上層節點廣播發送信標消息,下一層各節點接收到信標消息并立即記下本地的時間戳,將其發送到上層節點進行處理,節點計算和保存節點與參考節點時間的誤差值,并將其發送到對應節點完成時鐘誤差的修正。

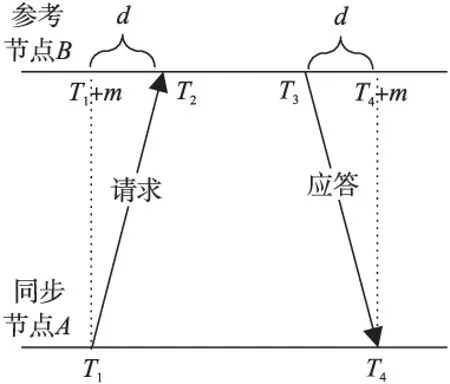
圖3 簇間通信算法

如圖3所示,T1、T4用來記錄同步節點的本地時間,T2、T3用來記錄參考節點的本地時間。同步節點A在T1時刻向參考節點B發送一個同步請求報文,報文中包含了同步節點的級別和T1,當參考節點B收到報文后,記錄下接收時刻T2,并立即向同步節點A回復一個同步應答報文,該報文中包含了參考節點B的級別和T1、T2以及回復時刻T3,同步節點A收到參考節點的回復后,記下時刻T4,假設來回報文的傳輸延遲相同為d,同步節點在T1時刻的時鐘偏差m為:

(1)

1.3 次網絡-簇內通信網絡

圖1中每個簇首節點與簇內節點形成的網絡稱為次網絡,次網絡拓撲如圖4所示,簇首節點使用單跳方式直接與簇內節點通信。由于接收簇內節點信息會消耗大量能量,簇首節點應在同步時盡量減少與簇內節點通信的次數,采用單向報文算法進行時間同步,如圖5所示。

圖4 次網絡拓撲

圖5 簇內通信算法

簇首節點在MAC層打時間戳t0的辦法去除發送延遲和訪問延遲。然后,簇首節點發送前導碼和起始字符等接收同步信息,再廣播時間分組。前導碼和起始字符的發送時間等于發送信息位的個數n和發送單位比特需要的時間t的乘積;接收節點在t1時刻收到廣播抵達時刻,并在修改本地時鐘之前保存時間t2,則接收處理延遲為t2-t1。假設忽略傳播延遲,接收節點與簇首節點同步,傳感器節點需要進行的時鐘調整為:

T=t0+nt+(t2-t1)

(2)

1.4 同步誤差補償機制

無線傳感器網絡時間同步協議中,消息傳輸延遲的計算精度決定了時間同步的精度。消息傳輸的非確定性延遲是影響父節點和子節點之間時間同步精度的主要因素[7]。節點通過交互同步信息估算相應的參數,然而同步信息在網絡上傳輸會產生一定時延,導致算法同步誤差與跳數距離成正比增長。同步誤差補償機制采用基于延遲估算的方法,使用線性回歸分析節點隨跳數變化造成的時間延遲變化情況,獲得時間延遲變化數據。傳感器節點根據自身到匯聚節點的跳數和獲得的時間延遲數據修正由于跳數距離增加造成的非確定性延遲增大[8]。

假設在一定時間范圍內節點時鐘晶振頻率是穩定的,給發送的每個字節標記時間,接收節點在接收完字節也做同樣的標記,如圖6所示。這樣在接收節點處獲得了多個時間標記對,對獲得的時間標記對構造最佳擬合直線T(time)。在誤差允許的時間間隔內,節點可直接通過T(time)計算某一時間節點間的時鐘偏移量,而不必通過發送時間同步消息來計算,從而減少了消息的發送次數并降低了系統能量開銷。

圖6 時間標記格式

通過線性回歸模型可以得到時鐘偏移量與同步時間的轉換公式[9]。

傳感器節點的時鐘偏移量如式(3)所示:

(3)

傳感器節點的同步時間修正如式(4)所示:

(4)

式(3)、式(4)中:發送端時戳為tbegin,接收端時戳為tend,那么同步節點與時鐘源節點的時間ttime=tend-tbegin,tlate是某一時刻節點間的時鐘延遲量,T是節點全局同步時間。

圖7 誤差補償包消息格式

未同步節點接收到已同步節點廣播的誤差補償包后,從消息包中得到本地時間與全局時間的同步誤差,調整自己的本地時間,使之與全局時間達到一致。

同步誤差補償機制解決了:①傳統分層或分簇算法中的時延增加;②時間同步精度降;③及節點不停地在監聽和發送之間轉換導致的能耗增加問題。

1.5 時鐘補償機制

網絡中每個節點維護各自的本地時鐘,節點利用晶體振蕩器驅動微處理器中的計數器以晶振振蕩頻率進行計數。無線傳感器網絡通常部署于室外環境中,溫度敏感的特性使得節點晶振頻率會隨著環境溫度的動態變化變得極不穩定。現實環境中無線傳感器網絡節點所處環境溫度的變化大,節點晶振輸出頻率會隨著其所處環境溫度的變化而變化。室外環境下節點晶振的不穩定性迫使節點必須頻繁地進行時鐘相偏的估計以及補償,以保證較高的時間同步精度[10]。然而,大多數時間同步算法的相偏估計過程主要依賴于節點間頻繁的時間戳交換,這種依賴于時戳交換的時間同步方法勢必會造成節點能量的迅速流失。

溫度-頻偏變化規律表現為一個二次函數[11],如式(5)所示。

f(t)=f0[1-k(T(t)-T0)2]

(5)

式中:f(t)為當前節點輸出頻率;fo為標稱頻率;k為溫度系數,即頻偏對溫度的敏感度,反映了節點晶振當前的穩定程度,通常情況下,k=-0.034±0.006ppm/℃;T0表示晶振測試時的標準溫度;T(t)代表當前溫度。頻率隨溫度的變化趨勢如圖8所示。

圖8 頻率隨溫度的變化趨勢圖

從圖8可以看出,溫度因素對節點頻偏值的影響十分巨大,比如:當溫度從25 ℃下降至10 ℃時,相應的頻偏變化為4ppm(即每秒4μs)。當傳感器節點長時間工作時,節點頻偏值的累積會十分巨大,所以節點在對頻偏進行估計時,為了提高估計精度,同步算法需要將溫度對頻偏的影響考慮在內。

節點頻偏主要是由其晶振頻率的漂移造成的,節點頻偏α(t)的獲取使得節點能夠根據當前溫度變化情況預測未來時鐘漂移的范圍,從而使節點可以通過數學計算補償時鐘漂移,對時間同步周期進行調節。因此節點頻偏為:

(6)

式中:f0為標準頻率,f(t)為節點當前頻率相關的函數。節點的當前頻偏可以通過對節點當前所處溫度的測量,并將測量結果代入式(5)、式(6)獲得。通過實驗獲得溫度-頻偏變化規律函數,在同步過程中,依賴于函數進行同步,無需時戳交換過程,因此有效地降低了通信開銷。

PSLTS算法基于以上幾種方法對無線傳感器網絡時間同步中的誤差進行兩次修正,算法整體流程如圖9所示。

圖9 算法流程圖

傳統時間同步算法的節點同步時間為:

T=tlocal+tlate

(7)

PSLTS算法的節點同步時間為:

TPSLTS=tlocal+tlate+f(Δt)

(8)

式(7)、式(8)中:tlocal為傳感器節點本地時間,tlate為同步延遲誤差時間,f(Δt)為晶振隨時間變化誤差函數。從公式可以看出,隨著節點運行時間的增加,傳統時間同步算法和PSLTS算法的同步時間差距越來越大,PSLTS算法可以更加準確的修正同步時間。

傳統算法如果需要長時間的全網節點時間同步,需要周期性執行算法進行重同步。時鐘補償機制通過對節點時間漂移進行估計,使得算法能夠在滿足特定同步精度的前提下只需要一次同步就可以長時間保持全網節點時間同步,可以有效的減少周期性同步造成的能耗損失。

2 實驗分析

針對PSLTS算法的時間同步性能,主要從2個方面描述PSLTS算法的性能特征:①時間同步精度;②通信報文開銷[12]。參與對比實驗的時間同步方法包括:①TPSN算法,②ATSP[13]算法。

2.1 算法復雜度分析

傳統時間同步算法在進行時間同步時,傳感器節點要與上層節點同步,并且需要周期性執行算法進行重同步,每一個傳感器節點T(n)=O(n2)。

PSLTS算法只需要在傳感器組網時獲取自身到匯聚節點的跳數,就可以自身進行修改。算法執行時間與傳感器節點的數量無關,時間復雜度為T(n)=O(1)。

2.2 同步精度分析

本文使用基于CC2530芯片的ZigBee節點進行實驗驗證本文算法的同步精度。算法每10min進行一次同步,進行五十次同步后,對每次同步后的時間誤差求取平均值。

PSLTS算法和ATSP算法、TPSN算法隨周期增加的誤差如圖10所示。

圖10 相同時間下同步誤差對比

PSLTS算法和ATSP算法、TPSN算法隨跳數增加的同步精度如圖11所示。由于采用了同步誤差補償機制,減小了多跳網絡中同步誤差的累積,時間偏移隨著跳數增加的幅度比較緩和,平均每跳的同步誤差控制在4μs以內。

圖11 不同跳數下同步誤差對比圖

2.3 時間漂移分析

使用CC2530芯片自帶的片上溫度傳感器獲取溫度信息。在不同溫度下PSLTS算法的時間漂移誤差如圖12所示。

PSLTS算法采用時鐘補償機制,減小了晶振由于時間漂移造成的誤差累積,時間漂移隨著時間增加的幅度比較緩和,使得算法可以長時間運行,不需要進行周期性同步。

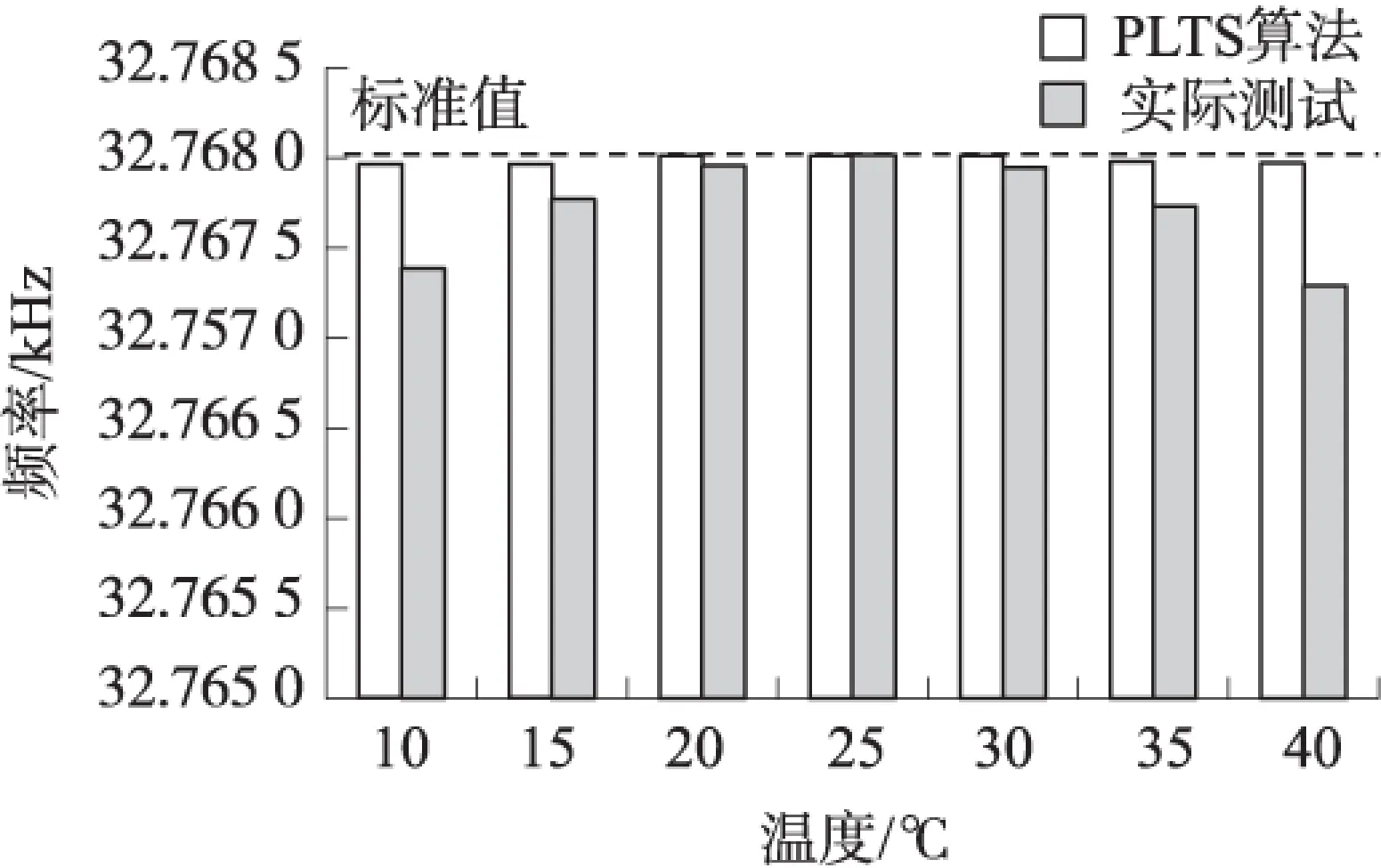
圖12 不同溫度時間漂移誤差對比

2.4 同步能耗分析

本節驗證PSLTS在無線傳感器網絡中的同步能耗。采用TinyOS2仿真軟件驗證本文算法的能量消耗。通過對不同跳數的ZigBee節點的時間誤差進行測量,仿真實驗中本文將節點的通信半徑設為20m,在100m×100m的區域內隨機布置了100個節點,簇首節點數量為10個,運行時間50min[10]。將RBS算法、TPSN算法同步周期設為10min。通過對同步報文開銷的計算得到傳感器節點的同步能耗。

圖13給出了平均同步能耗隨著節點數增加的變化趨勢,從圖13可以看出,隨著節點數的增多,PSLTS的能耗明顯小于ATSP和TPSN,且節點越多優勢越明顯。

平均能耗隨著運行時間增加的變化趨勢如圖14所示,隨著運行時間的增多,PSLTS的能耗開銷明顯小于ATSP和TPSN算法,且運行時間越長優勢越明顯。

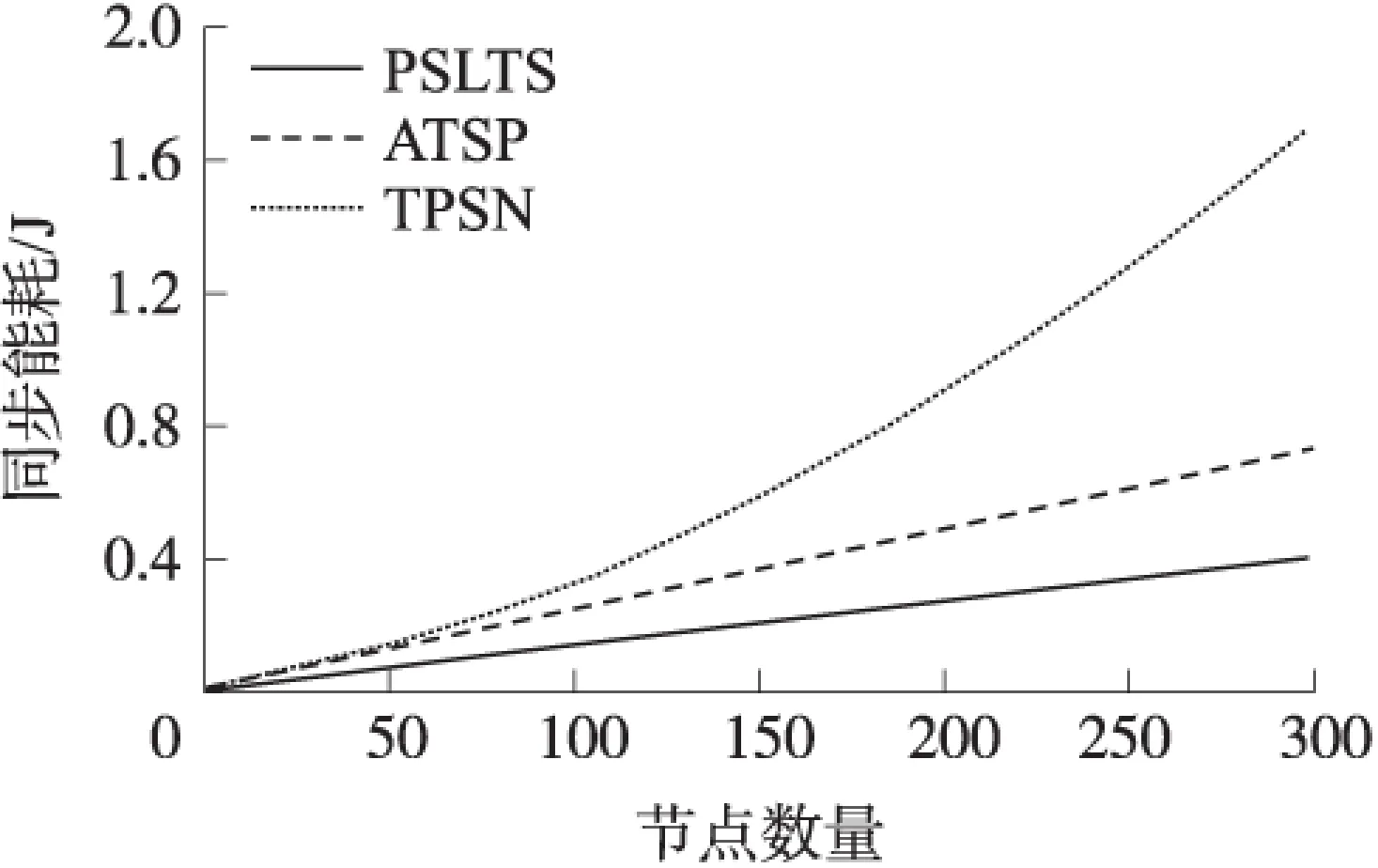
圖13 同步能耗隨節點數變化趨勢

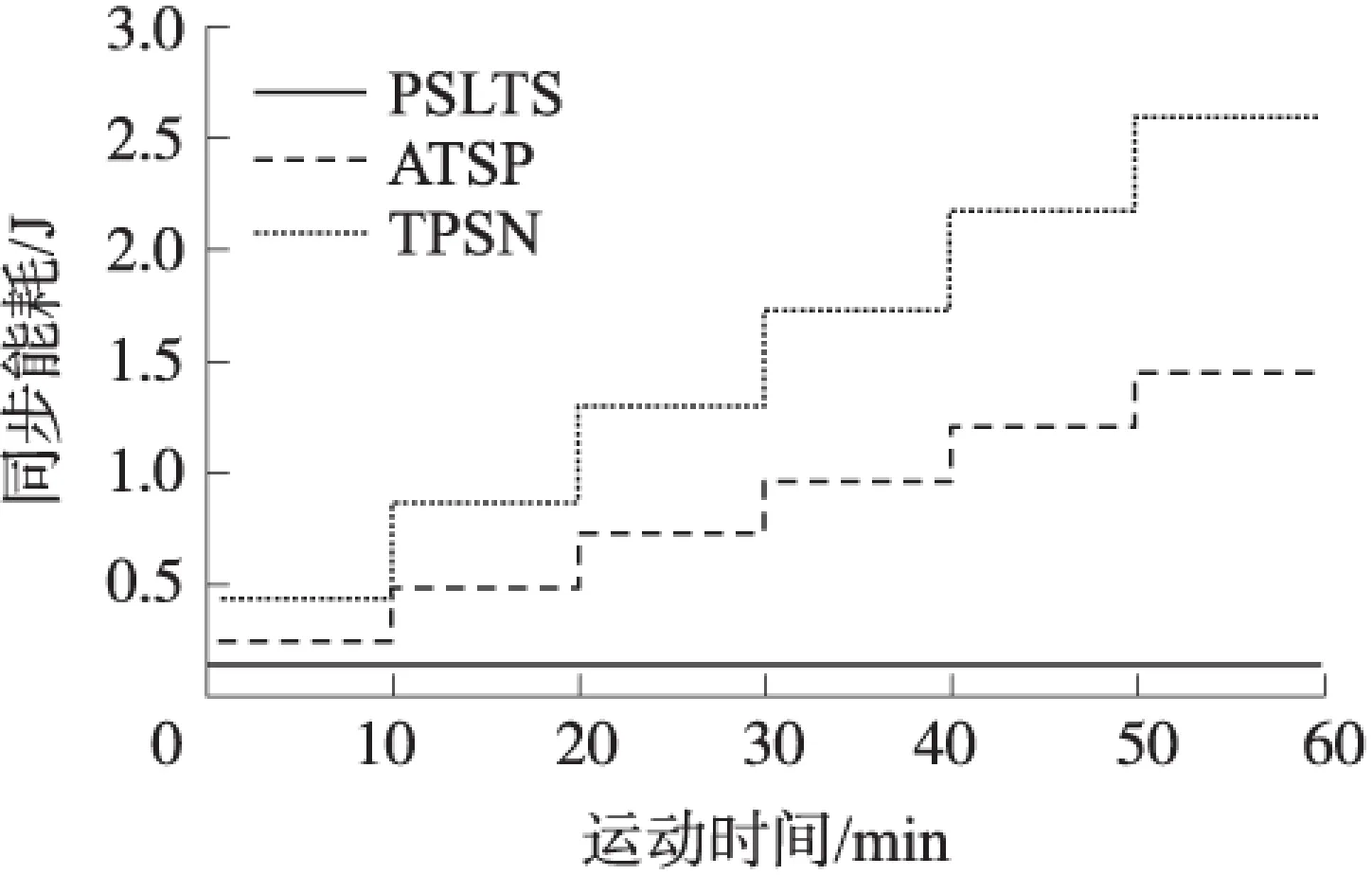
圖14 同步能耗隨運行時間變化趨勢

3 結論

針對無線傳感器網絡能量受限的特點和典型同步機制的不足,PSLTS算法結合單向廣播機制和雙向成對機制,并采用晶振補償策略,降低了同步次數,減少了同步通信開銷,延長了網絡的生命周期,更適用于能量受限的無線傳感器網絡的應用。由于時間延遲的不確定性,為獲得最優延遲時間,進行了大量實驗,并對獲取到的數據進行分析。算法中對晶振的影響因素只是考慮溫度,對于其他因素的影響還有待下一步繼續研究。

[1] 陶志勇,胡明. 基于等級層次結構的TPSN算法改進[J]. 傳感技術學報,2012,25(5):691-695.

[2] 許萬,楊光友,周晶晶. 基于RBS的無線傳感器網絡時間同步仿真研究[J]. Scientific Journal of Control Engineering,2013(3):64-70.

[3] 劉建娟. 基于改進螢火蟲群優化的無線自組網路由算法[J]. 傳感技術學報,2016,29(12):1905-1911.

[4] 李建洲,王海濤,陶安. 一種能耗均衡的WSN分簇路由協議[J]. 傳感技術學報,2013,26(3):396-401.

[5] Leva A,Terraneo F,Rinaldi L,et al. High-Precision Low-Power Wireless Nodes’ Synchronization via Decentralized Control[J]. IEEE Transactions on Control Systems Technology,2015,24(4):1-15.

[6] Sakuru K L V S P,Kondapalli S R R. Performance Evaluation of Sink Node Selection for Time Synchronization in WSN[C]//International Conference on Devices,Circuits and Communications. 2014:1-5.

[7] 孫子文,吳夢蕓,白勇. 抗延遲攻擊的WSN時間同步方法[J]. 傳感技術學報,2014,27(7):982-987.

[8] 吳寶明,李聲飛. 基于最優線性擬合的WSN時間同步算法研究[J]. 傳感技術學報,2010,23(12):1787-1791.

[9] Maggs M K,O’Keefe S G,Thiel D V. Consensus Clock Synchronization for Wireless Sensor Networks[J]. IEEE Sensors Journal,2012,12(6):2269-2277.

[10] Berger A,Pichler M,Klinglmayr J,et al. Low-Complex Synchronization Algorithms for Embedded Wireless Sensor Networks[J]. IEEE Transactions on Instrumentation and Measurement,2015,64(4):1032-1042.

[11] 金夢,陳曉江,房鼎益,等. 一種溫度自適應無線傳感網絡時間同步方法[J]. 軟件學報,2015,26(10):2667-2683.

[12] 徐久強,畢偉偉,朱劍,等. WSN中多跳均勻分簇路由算法的設計與仿真[J]. 系統仿真學報,2011,23(5):992-997.

[13] Wu J,Jiao L,Ding R. Average Time Synchronization in Wireless Sensor Networks by Pairwise Messages[J]. Computer Communications,2012,35(2):221-233.

杜永文(1974-),男,博士,副教授,研究領域為嵌入式系統;

馮 珂(1989-),碩士,研究生,研究領域為無線傳感器網絡;

彭 沖(1992-),碩士,研究生,研究領域為嵌入式系統。

WSN Time Synchronization Algorithm Based onHierarchical Dynamic Clustering*

DU Yongwen*,FENG Ke,PENG Chong

(Lanzhou Jiaotong University,The School of Electronics and Information Engineering,Lanzhou 730070,China)

Delay caused by multi-hop transmission and the inaccuracy crystal lead to a larger time synchronization error in WSN. In order to reduce the synchronization error,the traditional solution improves the frequency synchronization algorithm. It makes the traditional algorithm faces two problems:①high energy consumption used in the process of synchronization;②the imbalance between accuracy and energy consumption. Aiming at the above problems,a multi-layer dynamic clustering time synchronization algorithm for wireless sensor networks is proposed by combining one-way broadcast mechanism and bidirectional pairing mechanism. The algorithm reduces the cost of synchronous communication by adopting nodes stratification strategy. The synchronization error compensation mechanism is adopted to reduce the influence of synchronization errors. The clock compensation mechanism is used to reduce the accumulated error of the sensor nodes. Experimental results show that the proposed algorithm can prolong the life cycle of the network,reduce the frequency of synchronization and the consumption of communication under the premise of guaranteeing the accuracy.

wireless sensor network;time synchronization;delay;crystal oscillator

項目來源:甘肅省科技計劃項目(144NKCA040);國家自然科學基金項目(61163009)

2016-12-26 修改日期:2017-03-14

TP 212

A

1004-1699(2017)07-1070-06

C:7230

10.3969/j.issn.1004-1699.2017.07.017