吊艙推進的小型水面無人船航跡控制系統設計

燕聃聃,文元橋,肖長詩,張帆,周春輝

(武漢理工大學 a.航運學院; b.內河航運技術湖北省重點實驗室, 武漢 430063)

?

吊艙推進的小型水面無人船航跡控制系統設計

燕聃聃,文元橋,肖長詩,張帆,周春輝

(武漢理工大學 a.航運學院; b.內河航運技術湖北省重點實驗室, 武漢 430063)

為解決適應內河通航環境的小型水面無人船(USV)航跡控制的快速性和魯棒性問題，以小型水面無人船為研究對象，設計一種基于吊艙推進的USV航跡控制系統，該航跡控制系統由航跡控制器、航向控制器、轉向操作機構、電羅經、D-GPS，以及角度檢測傳感器組成。其中航跡控制采用改進的LOS(Line of Sight)導航算法；航向控制器由兩級模糊控制器構成，可同時滿足大角度轉向控制和小角度航向保持的性能要求。仿真和實船試驗結果皆表明，該控制系統能夠滿足內河復雜通航條件下USV對航跡控制的要求。

USV；LOS；模糊控制；航跡控制；吊艙

由于內河水域船舶通航密度大，航道彎曲，淺窄航段較多，氣象和水文環境復雜，對無人船航跡控制的要求很高。考慮到船舶操縱模型具有時變、非線性、時滯性和不確定性，以及內河通航環境的復雜性，模糊控制以其不需建立被控對象精確模型的優點被多數人采用[1-6]。與傳統的螺旋槳推進方式相比，吊艙推進具有機動性好、推進效率高、布置空間小等優點[7]，更適合內河水域船舶使用。針對吊艙推進式水面無人艇，以武漢理工大學iNav-Ⅰ無人船為研究對象，利用間接航跡控制方法設計船舶航跡控制系統。

1 系統原理

1.1 吊艙推進航跡控制系統基本框架

航跡控制系統原理見圖1。系統由2個閉環即航跡控制環(制導環)和航向控制環組成。航跡控制環將船位反饋裝置接收的船位信息與計劃航線比較，獲得船位偏差信息，通過制導算法得到命令航向作為航向控制環的期望值，用以消除航跡偏差；航向控制環將航向反饋裝置接收的航向信息與命令航向比較，求出舵令給船舶以消除航向偏差，從而實現船舶航跡控制。

1.2 吊艙推進航跡控制系統機械結構

控制系統機械結構見圖2。

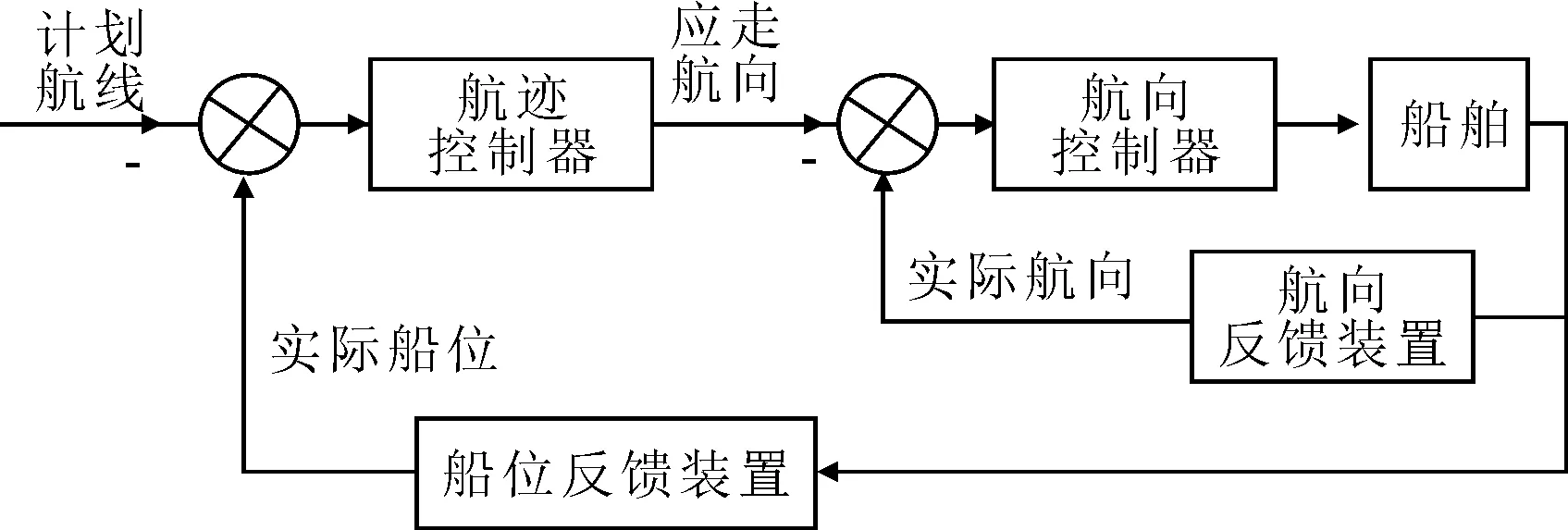
圖1 系統基本框架

圖2 控制系統機械結構示意

吊艙推進系統具有垂直貫穿于無人艇尾部甲板的主軸，主軸頂端裝有舵角測量儀，可直接測量舵角。舵角測量儀下面的主軸上套裝有聯軸器，聯軸器連接有圓錐齒輪，大小齒輪齒數比為5∶1，圓錐齒輪中的小齒輪連接有步進電機。步進電機與控制器構成驅動連接。主軸位于甲板下方的軸體上連接有吊艙，吊艙內置驅動電機，驅動電機輸出軸通過傳動軸連接螺旋槳。系統由步進電機提供轉向驅動力，吊艙內置驅動電機提供前進動力。

2 無人船航跡控制數學模型

2.1 響應型非線性無人艇數學模型

無人船轉艏運動一階非線性K-T方程為

(1)

式中：T為穩定性指數；K為回轉性指數；α為非線性系數。

考慮到橫向速度較小，其平面運動數學模型[8]可簡化為

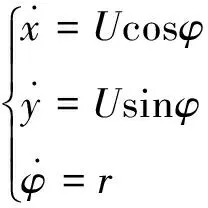
(2)

式中：(x,y)為重心坐標；φ為艏向角；U為船前進合速度；r為偏航角速度。

2.2 吊艙系統數學模型

吊艙推進航跡控制系統中，由步進電機給舵系統提供轉向驅動力。吊艙系統數學模型的建立主要取決于步進電機的轉速n、從上位機發出舵角控制命令到下位機控制單元接收到命令的時間t1，從下位機發出控制指令到步進電機開始反應的時間t2，從步進電機開始轉動到吊艙轉至設定值的時間t3。

假設期望吊艙轉向角的值為δpre，初始吊艙轉向角為δ0，且步進電機轉速一定，那么吊艙從δ0轉到δpre的時間為

(3)

經過實際測量計算，t1的數量級為100 ms，t2的數量級為10 ms。

3 航跡控制

3.1 航跡控制器

采用改進LOS(line-of-sight)導航算法，通過目標位置求得船舶的航向指令，船舶只要跟蹤指令航向即可有效地保持航跡。其實質就是把航跡劃分成一系列直線航跡段，當作直線航跡控制來對待，從而相應地簡化航跡控制器設計的復雜程度。原理見圖3，將船舶的航跡看成由關鍵點[X(k),Y(k)](k=1,2,3,…,N)組成的折線。

圖3 改進的LOS算法示意

d為t時刻船舶位置[x(t),y(t)]與計劃航線的距離。

1)如果滿足d>l,那么船舶的期望航向為

(4)

2)如果滿足d≤l,那么船舶的期望航向為

(5)

當船舶位置位于以關鍵點為圓心，ρ0為半徑的圓域時，對k值進行更新。

3.2 航向控制器

采用的航向控制器由2級模糊控制器[9]構成，當航向偏差(Δφ)大于某一角度時，采用第一級模糊控制器控制，實現船舶快速轉向；當航向偏差(Δφ)小于某一角度時，采用第二級模糊控制器控制，實現精確轉向。

圖4 e的隸屬函數

圖5 ec的隸屬函數

圖6 δ1的隸屬函數

輸出δ1的隸屬函數見圖6，論域[-35,35]。模糊規則見表1。

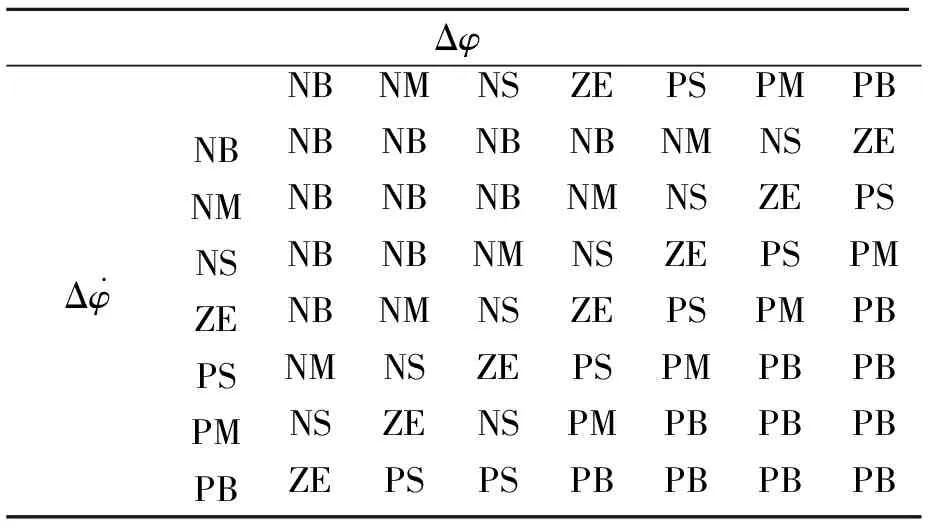
表1 第一級模糊控制規則

2)第二級模糊控制器。由于第一級模糊控制器輸入為偏差和偏差變化率，存在控制死區，會產生控制誤差，需要增加一個積分環節。如果只用一級模糊控制器，也就是說第一級模糊控制器中采用三輸入，即偏差、偏差變化率、偏差積分，那么模糊規則將有7×7×7=343條。如果采用雙極控制器，并且第二級控制器由一個模糊PD控制器和一個模糊PI控制器，那么模糊規則數量將大量減少，并且能夠消除部分誤差，獲得較好的控制效果。模糊PD控制器輸入的隸屬度函數見圖7、8，量化因子分別為0.133和0.02。輸出的隸屬度函數見圖9。控制規則與第一級模糊控制器相同。

圖7 Δφ的隸屬度函數

圖的隸屬度函數

圖9 δ21的隸屬度函數

模糊PI控制的輸入為航向偏差Δφ和航向偏差積分，將Δφ，∫Δφ和輸出控制量的數量范圍劃分為5個語言變量表述的模糊集，即負大(NB)、負小(NS)、零(ZE)、正小(PS)、正大(PB)。∫Δφ的論域為[-8,8]，量化因子為0.02。輸出量δ22的論域為[-10,10]。其隸屬函數見圖10～12。模糊規則見表2。

圖10 Δφ的隸屬函數

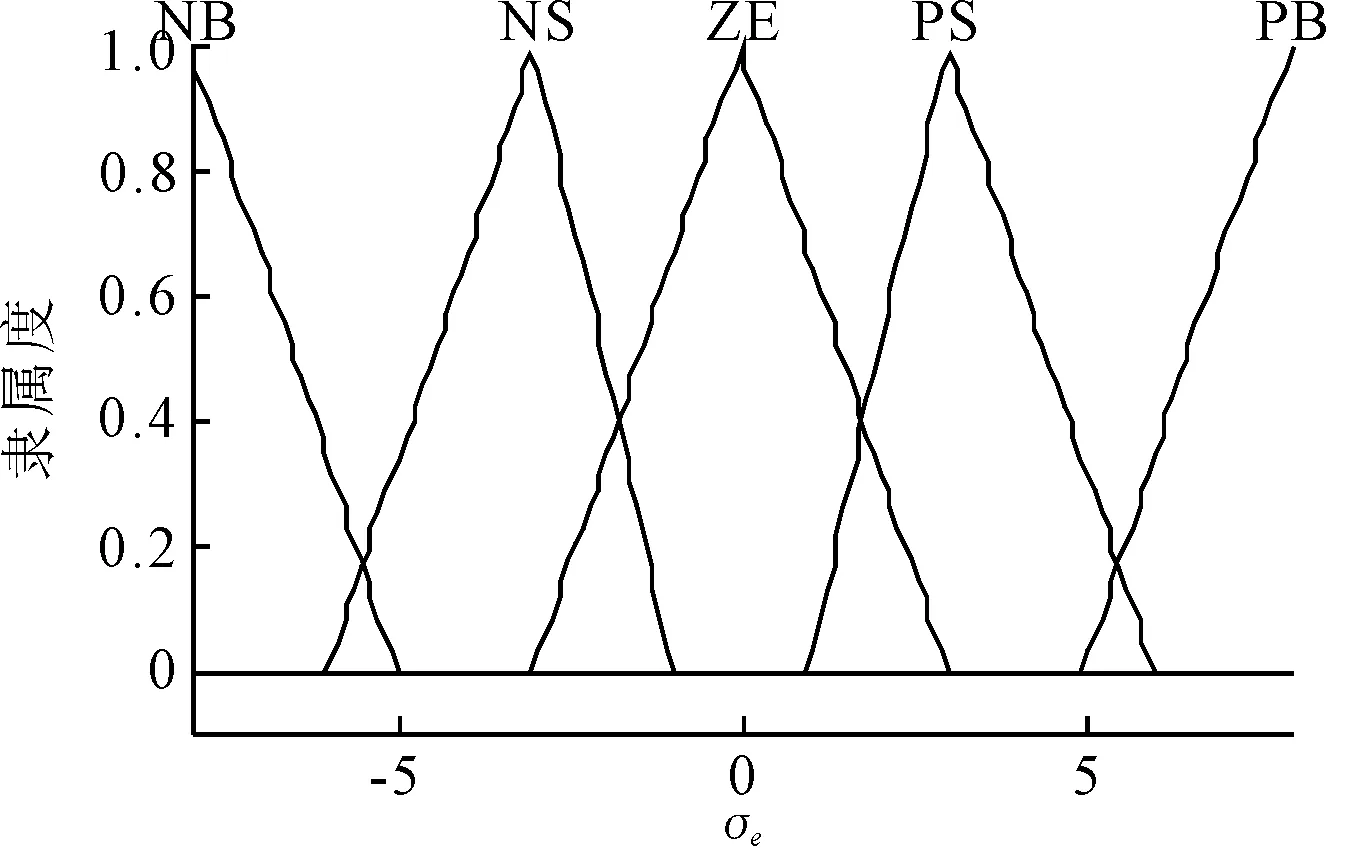
圖11 ∫Δφ隸屬函數

圖12 δ22的隸屬函數

表2 第二級模糊控制器模糊積分控制規則

4 仿真實驗

為了驗證無人船航跡控制系統的控制效果，選擇武漢理工大學iNav-Ⅰ無人船進行航跡跟蹤控制實驗，無人船相關參數見表3。

表3 iNav-I無人船基本參數

表中參數K、T由Z型實驗和旋回實驗結果進行參數辨識求得。無人船的初始位置為坐標原點(0,0)，初始艏向角為正北方向，ρ0和l都取值5 m。無人艇的航路點設置見表4。

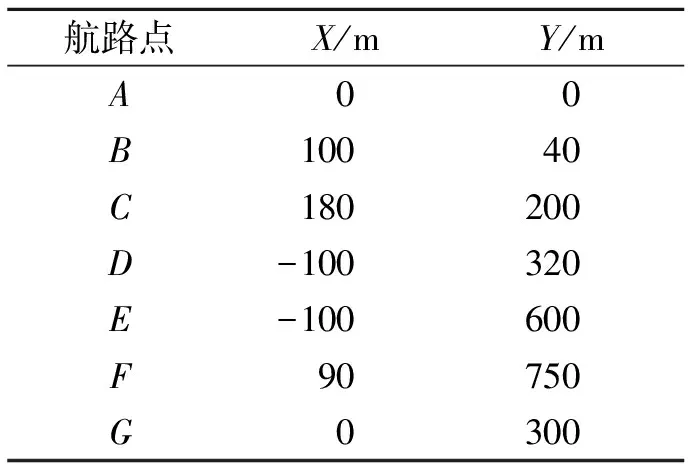
表4 設計航路點

為了使得仿真效果更真實，加入風浪流的干擾。將海流的干擾作用等效為10°的恒值干擾，風浪的干擾作用則通過白噪聲和一個二階波浪傳遞函數來模擬。

設定仿真海況為風力四級，大浪，具體參數[10]為Kω=0.1979,σm=0.544，ω0=0.606。仿真結果見圖13～15。

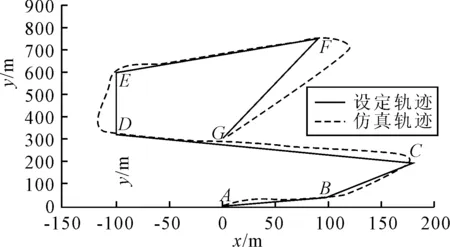
圖13 干擾條件下的無人船航跡保持軌跡

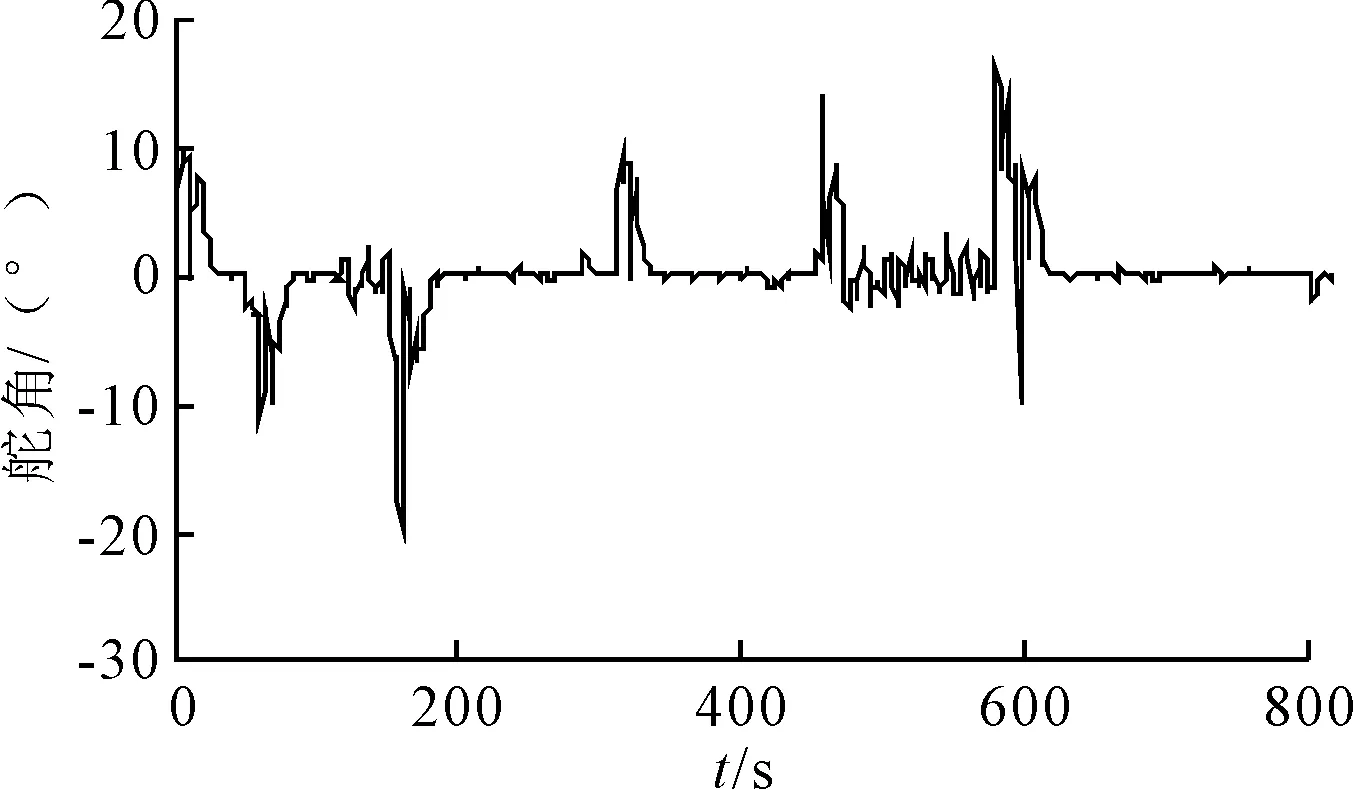
圖14 干擾條件下控制器的輸出舵角

圖15 有干擾條件下局部放大航跡

根據以上仿真結果可以看出，在上述干擾條件下，所設計的基于雙極模糊控制和改進LOS航跡制導的航跡控制器基本能夠完成航跡控制任務。由圖13可見，無人船能夠沿著設定航跡航行。在穩定階段，航跡與設定航跡的垂直誤差約為5 m，這個距離剛好與改進LOS算法中d的距離相同，說明航跡控制效果良好。但是在轉向點F附近轉向時，轉向角較大，有將近30 m以上的誤差。分析其原因，一方面由于d設置為5 m，只有當無人船在距離F點5 m的圓域內，才判定無人船到達F點，繼而進行轉向，打舵時間較晚；另一方面由于吊艙式推進器的響應具有一定的延時，實際舵角并沒有達到控制器的輸出值。

由圖14可見，無人船舵角的變化規律是：無人船在轉向角進行轉向時，會先打出較大舵角，在轉向即將結束時，航向逐漸趨于穩定，無人船的舵角也趨向于0°，基本符合實際情況。

6 實船驗證

無人船航跡控制的實船試驗在武漢東湖水域進行，試驗中船舶的平均航速1 m/s，湖面稍有風浪。

設定航跡關鍵點見表5。

進入航跡控制后，無人船的運動軌跡見圖16。

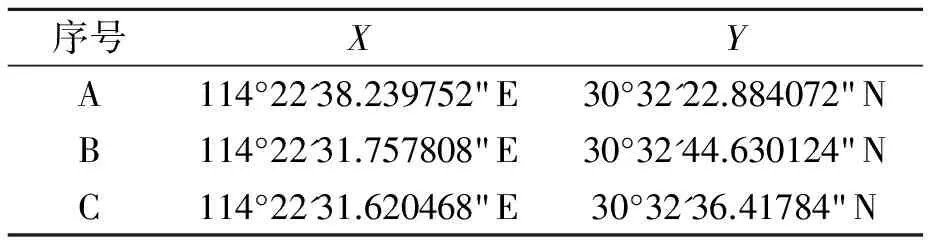
表5 設計航路點

圖16 無人船航跡控制實船試驗結果

由圖16可見，所設計的航跡控制器在實際中可以完成航跡控制目標，說明所設計的間接控制系統是有效的，可行的。但就控制效果而言，AB段和CA段誤差較大，最大誤差甚至達到43 m左右，BC段誤差較小，但最大也有20 m。

7 結論

1)以吊艙推進型小型無人船為研究對象，采用改進的LOS制導算法和雙極模糊算法對船舶航跡控制進行系統研究，并應用于實船實驗中，為解決內河環境下無人船路徑規劃、避碰等問題奠定了理論和實踐基礎。

2)仿真時，當轉向角較大時，航跡偏差較大，一方面與ρ0值相關，另一方面由于模糊規則和隸屬函數一旦確定，便不可調節，下一步應從這兩方面進行改進。

3)針對實船實驗誤差較大的問題，可考慮增加舵角控制環，對吊艙的轉向進行反饋控制，便于進一步減小誤差。

[1] VUKIC Z, OMERDIC E, KULJACA L. Improved fuzzy autopilot for track-keeping[C]. Proceedings of the IFAC Conference on Control Applications in Marine Systems.1998.

[2] OMERDIC E, ROBERTS G N, VUKIC Z. A fuzy track-keeping autopilot for ship steering[J]. Journal of marine engineering and technology,2003(2):23-35.

[3] FRAGA R, SHENG L. Double fuzzy logic control for the ship path following[C]. Intelligent Control and Information Processing(ICICIP),2011 2ndInternational Conference on. IEEE,2011.

[4] FRAGA R, SHENG L. Fuzzy technique tracking control for multiple unmanned ships[J]. Research Journal of Applied Sciences,2013,5(2)：538-545.

[5] 郝陽,趙新華.船舶航跡自校正模糊自動駕駛儀設計[J].控制工程,2014(增刊1):73-75.

[6] 董早鵬,劉濤,萬磊,等.基于Takagi-Sugeno模糊神經網絡的欠驅動無人艇直線航跡跟蹤控制[J].儀器儀表學報,2015,36(4):863-870.

[7] 馬騁.吊艙推進技術[M].上海：上海交通大學出版社，2009.

[8] 王波.基于滑模的船舶直線航跡控制設計及優化[D].大連：大連海事大學,2014.

[9] YAN Dandan, XIAO Changshi. Pod propulsion small surface USV heading control research[C].Proceedings of the International Offshore and Polar Engineering Conference.2016：630-635.

[10] 葛增魯.無人艇航向運動控制器的設計與實現[D].大連：大連海事大學，2016.

Development of Tracking Control System for the Pod Propulsion Small Surface USV

YAN Dan-dan, WEN Yuan-qiao, XIAO Chang-shi, ZHANG Fan, ZHOU Chun-hui

(a.School of Navigation; b.Hubei Key Laboratory of Inland Waterway Transport Technology;Wuhan university of technology, Wuhan 430063, China)

To solve the problems of speed and robustness of track control for small unmanned surface vehicle (USV) in the inland water navigation environment, a USV track control system was designed based on the pod propulsion, which was compose of track controller, course controller, steering mechanism, electronic compass, D-GPS and rudder angle measuring instrument. The improved LOS (Line of Sight) navigation algorithm was used by the track controller. The heading controller included two fuzzy controllers, which can meet the requirements of large-angle steering control and small-angle course keeping. The simulation results of real ship sailing experiments showed that this control system can meet USV’s requirement of track control under complex conditions of inland navigation.

USV; LOS; fuzzy control; track control; POD

10.3963/j.issn.1671-7953.2017.04.048

2016-12-05

國家自然科學基金(51579204)

燕聃聃(1992—)，女，碩士生

研究方向：智能航海與船舶控制

U675.79

A

1671-7953(2017)04-0210-06

修回日期：2017-01-18