聚乙烯單鏈量子熱輸運的同位素效應?

吳宇1)2) 蔡紹洪1)3)? 鄧明森3)4) 孫光宇2) 劉文江1)3) 岑超2)

1)(貴州大學大數據與信息工程學院,貴陽550025)

2)(貴州師范學院物理與電子科學學院,應用物理研究所,貴陽 550018)

3)(貴州財經大學貴州省經濟系統仿真重點實驗室,貴陽 550025)

4)(貴州師范學院貴州省納米材料模擬與計算重點實驗室,貴陽 550018)

聚乙烯單鏈量子熱輸運的同位素效應?

吳宇1)2) 蔡紹洪1)3)? 鄧明森3)4) 孫光宇2) 劉文江1)3) 岑超2)

1)(貴州大學大數據與信息工程學院,貴陽550025)

2)(貴州師范學院物理與電子科學學院,應用物理研究所,貴陽 550018)

3)(貴州財經大學貴州省經濟系統仿真重點實驗室,貴陽 550025)

4)(貴州師范學院貴州省納米材料模擬與計算重點實驗室,貴陽 550018)

(2017年1月20日收到;2017年3月27日收到修改稿)

高分子導熱材料的有效調控受到了日益廣泛的關注.應用密度泛函理論(DFT)、中央插入延展(central insertion scheme,CIS)方法及非平衡格林函數(NEGF)理論,對包含432個原子、長18.533 nm的聚乙烯單鏈量子熱輸運的同位素效應進行了研究.計算結果表明,室溫下長100 nm的純12C聚乙烯單鏈的熱導率理論上限高達314.1 W·m?1·K?1;對于12C聚乙烯單鏈,其他條件一定時,14C摻雜引起的熱導同位素效應比13C更為顯著;室溫下純12C聚乙烯單鏈中14C摻雜原子百分數為50%時同位素效應最顯著,此時平均熱導比未摻雜時下降了51%.這對探索聚乙烯材料熱輸運的同位素影響機理具有十分積極的意義.

聚乙烯單鏈,量子熱輸運,平均熱導,同位素效應

1 引言

隨著納米電子技術的進步,有機聚合物分子器件的制備與應用取得了極大的進展.目前世界上最小的發光二極管已由聚噻吩分子鏈實現[1],而良好的導熱能力是提高其性能的必要條件.事實上,聚噻吩鏈具有十分優異的導熱性能及良好的熱穩定性[2],已用于汽車表面散熱材料中.有機聚合物分子鏈的導熱能力及其可調控性受到了越來越廣泛的關注.

聚合物塊體通常被視為絕熱材料,熱導率約為0.1 W·m?1·K?1[3].室溫下,聚乙烯塊體的熱導率約為0.35 W·m?1·K?1[4];用納米孔模板浸潤法制備的聚乙烯納米線陣列的熱導率可比聚乙烯塊體提高一個數量級,室溫下約為2.2 W·m?1·K?1[5];而有序化程度更高的超高分子量聚乙烯材料,表現出更好的導熱特性,如沿纖維方向彈性模量為134 GPa的高強度聚乙烯在140 K溫度下的熱導率可達到50 W·m?1·K?1.超高分子量聚乙烯與環氧樹脂組成的復合材料在140 K溫度下的熱導率可達100 W·m?1·K?1,已用于高溫超導線圈的傳導冷卻[6].文獻[7]理論探討了聚乙烯單鏈與碳納米管復合后導熱性能的提升,這些都與聚乙烯單鏈的熱輸運性質緊密相關.

實驗發現,超拉伸后晶體化的聚乙烯納米纖維的熱導率甚至可高達104 W·m?1·K?1[4],比聚乙烯塊體材料的熱導率提高了約300倍,遠高于鉛、鎳、鐵等一般金屬的熱導率,與黃銅(含鋅30%)的熱導率108.9 W·m?1·K?1相當[8].這說明聚乙烯單鏈本身的熱導率相當高,影響聚乙烯塊體熱導率的主要因素是各聚乙烯單鏈的有序程度、晶鏈長度、雜質含量、缺陷以及微觀接觸狀態等.

實際測試過程中接觸形變、雜質、缺陷等因素的存在,會使測量得到的聚乙烯單鏈的熱導率偏低,因而實驗確定純12C聚乙烯單鏈熱導率的上限難以實現.另外,單一因素(如同位素摻雜)條件下實現聚乙烯單鏈熱導率的測定十分困難.事實上,同位素效應是影響材料熱輸運性質不容忽視的因素.將1.1%(原子百分數)的13C同位素雜質從金剛石晶體中去除后,熱導率提高了35%[9].石墨烯的熱輸運性能呈典型的各向異性[10],且受邊緣形狀、缺陷、應變等影響[11?13],其熱輸運的同位素效應在理論[14?16]和實驗方面都有了較為深入的研究.實驗表明,室溫附近高純度的12C石墨烯帶摻入50%的13C原子后,熱導率幾乎減半[17].因此,認識純12C聚乙烯單鏈導熱能力的理論上限并討論影響其熱物理性能的同位素因素十分必要.

目前對聚乙烯單鏈導熱性能的理論研究多數集中于分子動力學(MD)方法[3,6,18,19],這對減少計算量大有裨益,但MD方法的計算結果高度依賴于勢函數的選擇.用不同的勢函數(Terso ff勢和AIREBO勢)研究同一石墨烯體系的熱導同位素效應,在某些摻雜比例下,得到的熱導率甚至相差14%[20].即使采用同一種勢函數(AIREBO勢)對聚乙烯單鏈的熱導率進行研究,結果差異也可能很大.室溫下,Green-Kubo方法結合模態分解方法得到40 nm長度以上的聚乙烯單鏈熱導率超過100 W·m?1·K?1[3],而用非平衡分子動力學(NEMD)方法計算得到160 nm長的聚乙烯單鏈熱導率僅為57 W·m?1·K?1[7].因此,采用第一性原理計算及非平衡格林函數(NEGF)方法對聚乙烯單鏈的導熱能力及其影響因素進行系統研究十分必要.文獻[21]用密度泛函理論(density functional theory,DFT)和NEGF方法計算了純12C聚乙烯單鏈的聲子透射譜,但正如該文獻所分析的那樣,由于計算誤差的存在,聲子振動的旋轉對稱性被破壞,聲子透射譜低頻極限欠準確;另外,由于沒有采取頻率校正工作,得到的聲子振動頻率整體偏高.本文第2節采用的對稱性保持和頻率校正方法有效地克服了上述兩個缺點.文獻[22]系統回顧和總結了分子動力學和第一性原理方法結合非平衡格林函數研究低維納米材料量子熱輸運的成果.通常情況下,同位素效應包含一定的隨機因素,若計算體系原子數目太少則難以體現統計效應,而直接對包含數百個原子的聚乙烯單鏈力常數張量進行第一性原理計算,則工作量極大,給精確研究導熱性能及其同位素效應帶來了巨大的困難.

本文采用密度泛函理論、中央插入延展(central insertion scheme,CIS)方法[23,24]、非平衡格林函數[25,26]理論在第一性原理的基礎上研究了聚乙烯單鏈熱導的同位素效應.第2節詳細介紹了本文計算聚乙烯單鏈熱導及其同位素效應的過程,我們可以看到該方法有效克服了級聯散射模型和標度理論只能處理低濃度同位素雜質聲子散射的不足.第3節詳細討論了分別摻雜13C與14C元素后聚乙烯單鏈熱導的同位素效應.

2 計算模型與方法

同位素摻雜的聚乙烯單鏈如圖1所示.在我們的計算模型中,散射區包含72個聚乙烯單胞,共計432個原子,散射區長度L=18.533 nm,左、右兩端為半無限長聚乙烯單鏈熱極.

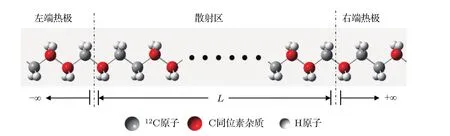
圖1 (網刊彩色)聚乙烯單鏈隨機同位素雜質構型示意圖Fig.1.(color online)Illustration of a polyethylene chain which contains random isotope con fi gurations.

由于研究的體系為納米尺度,聲子平均自由程以內體系熱導率與聲子輸運的長度成正比,這與擴散輸運的情況大相徑庭,此時的輸運過程為彈性輸運,體現出典型的量子輸運特征,通常用于描述擴散輸運的傅里葉導熱定律此時不再適用[22,27?30].若忽略聲子間相互作用與電、聲子間相互作用,且考慮到同位素雜質隨機分布的聲子透射系數的統計平均效應,平均熱導率Kph的Landauer公式為[31,32]

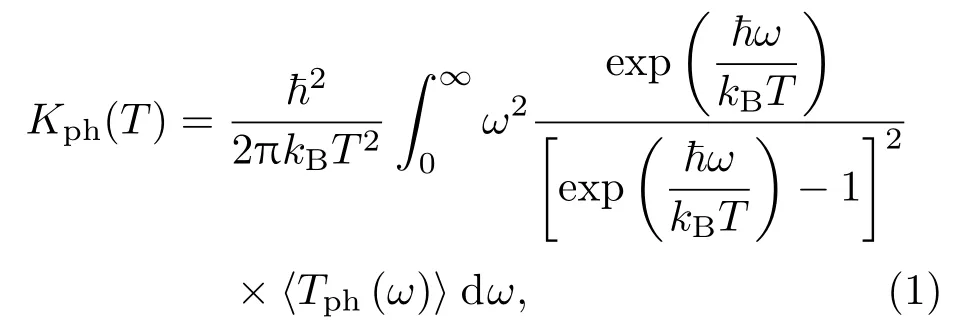
式中~為約化普朗克常數,kB為玻爾茲曼常數,ω為聲子頻率,T為體系的熱力學溫度,聲子透射系數Tph(ω)計算公式為

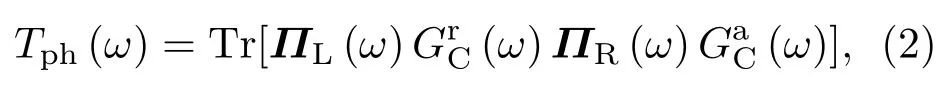
式中分別為量子輸運體系的滯后格林函數和超前格林函數,描述聲子通過中間散射區域的能力,ΠL(ω),ΠR(ω)分別表示左、右熱極的自能矩陣.

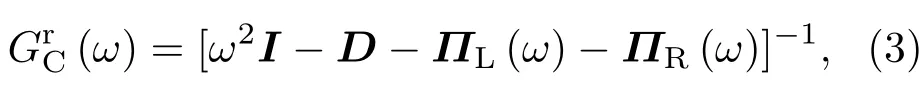
式中I為單位陣,D為散射區域的動力學矩陣,定義為

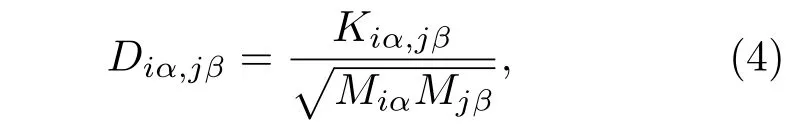
式中M為原子質量,力常數二階張量Kiα,jβ的定義為

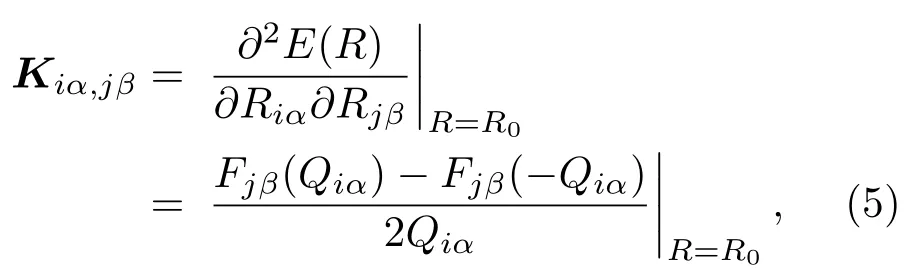
式中i,j為原子編號,α,β={x,y,z}表示空間的三個正交方向,E為微觀體系的總能量,Qiα為第i個原子α方向的小位移量,F為原子間的相互作用力,R表示體系各原子的空間位形,Riα和Rjβ分別表示第i個原子的位置矢量在α方向上的投影和第j個原子的位置矢量在β方向的投影.

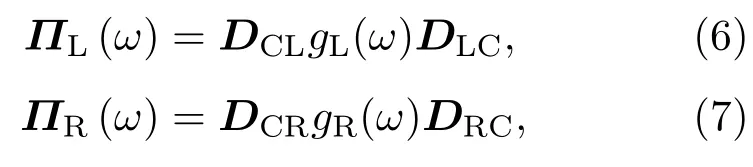
式中DCL,DLC與DCR,DRC分別為左、右熱極與中間散射區域的耦合矩陣,且DLC=DTCL,DCR=DTRC.gL(ω),gR(ω)分別是左、右熱極的表面格林函數.帶寬函數ΓL,R=?2ImΠL,R由自能函數的虛部得到,分別體現中間散射區域與左、右熱極的耦合.

為了考慮同位素隨機摻雜的平均效應,我們對每一種特定的同位素摻雜比例,選取30個隨機同位素雜質構型,逐一計算各隨機構型下的透射系數(100%摻雜除外,因為這實際就是純聚乙烯單鏈,透射系數和熱導都不存在隨機性,此時平均熱導與熱導相同),再取算術平均后得到該摻雜比例下的平均透射系數?Tph(ω)?以及平均熱導Kph.

聚乙烯單鏈的優化和力常數張量的計算采用量子化學軟件Gaussian 09[33].DFT計算選用雜化密度泛函B3LYP及6-31G基組,優化后相繼三個C原子構成的夾角為113.466?,C—C鍵長為1.539 ?(1 ?=0.1 nm),C—H鍵長為1.101 ?,沿聚乙烯單鏈方向的晶格常數為2.574 ?,與透射電子顯微鏡衍射圖像測得的晶格常數2.544 ?相當接近[4].構建的超胞含7個單胞,在周期性邊界條件(PBC)下優化后得到體系能量最低的穩定幾何結構,并保證體系中各原子最大受力均小于10?3eV/?,在此基礎上,計算體系的力常數張量,并使最終獲得的力常數張量保持原體系的物理對稱性不發生改變[34,35].

CIS方法在高效計算大型準周期結構電子體系和量子輸運中已經得到了廣泛的驗證和應用[36?38].我們在獲得超胞體系力常數張量的基礎上,通過CIS方法構造了18.533 nm聚乙烯單鏈體系的力常數張量,極大地減小了計算量.針對DFT用B3LYP雜化泛函和6-31G基組算出的振動頻率通常比實驗值偏高的情況,對CIS方法得到的聲子透射譜進行計算化學比較和基準數據庫(CCCBDB)的頻率校正[39].根據選用的泛函和基組,校正因子取為0.962,則得到的聲子透射譜以及熱導值將和實驗更加一致,具有較高的準確性.

由于同位素雜質的出現,聲子在傳播過程中會發生散射,處理納米體系聲子與雜質散射時除了常見的級聯散射模型之外[40?42],還有標度理論[43,44].雖然這兩種方法之間有些差異,但二者都假定聲子與各個同位素雜質的散射互相獨立,整個體系的散射可看作聲子同各雜質單道散射的疊加.這兩種方法直觀簡便,也能在一定程度上解釋量子熱輸運的同位素效應,但多道散射引起的關聯效應被忽略[41],僅對于隨機同位素雜質濃度較低(6 10%)時才有比較準確的結果[16,41].

為了克服該局限性,我們在獲得18.533 nm聚乙烯單鏈力常數張量的基礎上,直接隨機抽樣模擬同位素雜質隨機分布,進而獲得體系的動力學矩陣,對聚乙烯單鏈在不同摻雜比例下的平均熱導進行研究.值得注意的是,該方法完全從量子力學出發,對聲子與同位素雜質的散射條件不作任何限制,將聲子散射作為一個整體加以考慮,理論上能較為準確完整地描述任意比例摻雜的熱導同位素效應.

根據C原子的自然豐度,先研究沒有同位素雜質時純凈聚乙烯單鏈的熱導,即先考查以12C作為組分的純凈聚乙烯單鏈的熱輸運規律,再研究分別單獨摻入13C,14C雜質時熱導的同位素效應.

3 結果與討論

通過CIS方法將體系的力常數張量進行擴展,極大地提高了計算效率,從而可以在第一性原理精度上處理18.533 nm長聚乙烯單鏈的同位素摻雜聲子散射問題.這一計算量對DFT而言通常是難以直接實現的.計算結果表明,用CIS方法得到的18.533 nm長純12C聚乙烯單鏈的聲子透射譜,和用密度泛函微擾理論(DFPT)方法計算的聲子透射譜[45]完全一致,這印證了提出方法的正確性.

圖2中純12C聚乙烯單鏈聲子透射譜呈典型的臺階特征,量子化熱導的基本單元為K0=(h為普朗克常數)[46],由第一個量子化臺階特征可看出,體系在低頻極限時透射系數Tph=4,與一維無限長完好的納米管或石墨烯帶聲子透射系數的理論低頻極限一致,這是由三個剛性平動自由度和一個繞一維軸線旋轉的自由度決定的[34].根據聚乙烯拉曼光譜的測定結果,CH2基團的不對稱伸縮振動頻率在振動體系中最高,接近3000 cm?1,與此相應,圖2中數據表明CH2基團不對稱伸縮振動頻率約為2925 cm?1,與拉曼光譜實驗測定的2882 cm?1基本一致[47],這也說明了頻率校正工作的有效性.摻入25%的13C同位素雜質后,聲子透射譜的臺階特征被嚴重破壞,體現出雜質對聲子的強烈散射,各頻段聲子透射譜均出現了不同程度的削弱,聲子透射譜與橫軸包圍的面積明顯變小,聲子透射能力顯著下降.

為了考察各不同頻率聲子對熱導的貢獻,將(1)式的被積函數在T=500 K條件下作無量綱化處理,除以其在整個積分區間內的最大值,得到不同頻率聲子對熱導貢獻的相對強度r(ω).現以純凈12C聚乙烯單鏈的不同頻率聲子對熱導的貢獻為例,從圖3可以看出,隨著頻率ω的增加,如ω>1000 cm?1后,聲子對熱導的貢獻迅速減小,高于1500 cm?1的振動模式對熱導幾乎沒有貢獻.由此可見,低、中頻段聲子的透射能力對體系熱導的貢獻起決定作用,而接近3000 cm?1高頻段聲子對熱導的貢獻完全可以忽略不計.

圖2100 %12C和25%13C同位素摻雜的平均透射譜Fig.2.Average phonon transmission spectra of polyethylene chains with pure12C and with 25%13C isotope concentration.

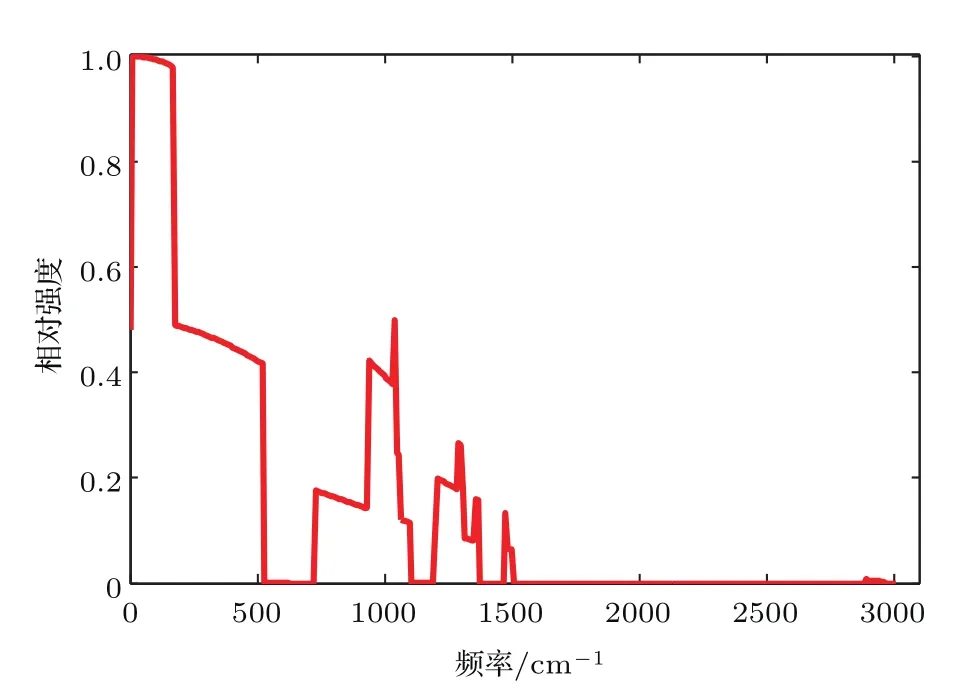
圖3 T=500 K時不同頻率聲子對熱導貢獻的相對強度Fig.3.The relative intensity of a phonon contributing to the thermal conductance at di ff erent frequencies at 500 K.

繼續摻入50%的13C原子,則聲子透射譜與橫軸包圍的面積變得更小(圖4).再增加雜質濃度,當聚乙烯單鏈中C原子全為13C時,體系又重新成為純凈的聚乙烯單鏈,此時透射譜重新恢復臺階化特征.這恰好說明了同位素雜質概念的相對性,如在純12C聚乙烯單鏈中摻雜25%的13C,與純13C聚乙烯單鏈中摻雜75%的12C是完全等價的,低摻雜與高摻雜濃度的概念也完全是相對的,故而標度理論的觀念存在局限.該透射譜形狀與純凈12C聚乙烯的透射譜非常相似,只是整個譜向低頻方向略微移動,這是由體系力常數張量保持不變,僅C原子量增加,各聲子振動頻率稍稍降低引起的.

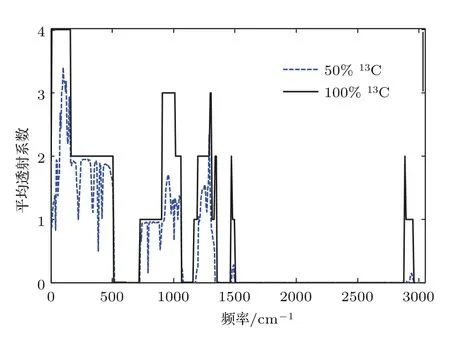
圖450 %13C同位素摻雜和100%13C的平均透射譜Fig.4.Average phonon transmission spectra of polyethylene chains with13C isotope concentrations of 50%and 100%.

從圖5可以看出,隨著體系溫度的升高,越來越多的聲子振動模式被激發出來,體系的平均熱導隨溫度升高而單調增加,但是增長率逐漸減小.相同溫度下,對于純12C聚乙烯單鏈,隨著13C摻雜濃度的逐漸增高,體系的平均熱導先變小,后變大,其中100%12C與100%13C的一對曲線、16.7%12C與83.3%13C的一對曲線十分接近,而25%12C與75%13C的一對曲線幾乎重合.純12C聚乙烯單鏈的熱導只比純13C聚乙烯單鏈略大.相同溫度下,聚乙烯單鏈中12C,13C各占50%時,平均熱導達到最小值.

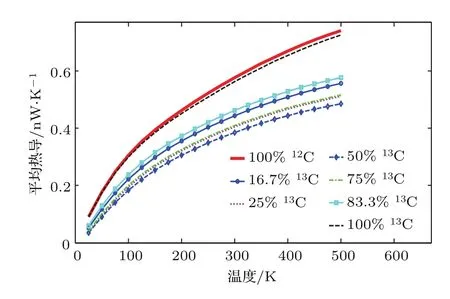
圖5 (網刊彩色)聚乙烯單鏈中各種同位素摻雜比例下的平均熱導溫度曲線Fig.5.(color online)Average thermal conductance versus temperature for polyethylene chains with different isotope compositions.

從圖6可以看出,在彈性輸運條件下,溫度為300 K時,純12C聚乙烯單鏈的熱導Kph=0.577 nW·K?1,且不隨鏈長改變,在聲子平均自由程內熱導率σ與散射區長度L成正比,σ=KphL/A[32],其中A為聚乙烯單鏈的橫截面積.室溫下石墨烯的聲子平均自由程約為775 nm[48],本文與文獻[21]的觀點一致,即純凈的聚乙烯單鏈和石墨烯一樣具有可觀的彈性輸運長度,室溫下聲子平均自由程大于100 nm.若取L=100 nm,根據聚乙烯晶體材料的測定結果[49],可得聚乙烯單鏈的橫截面積A=18.37 ?2.從而得到室溫下100 nm長的純12C聚乙烯單鏈的熱導率為314.1 W·m?1·K?1.由于計算過程中沒有考慮聚乙烯單鏈中實際存在的缺陷、形變,以及聲子間相互作用等因素引起的聲子散射,因而該結果為100 nm長純12C聚乙烯單鏈熱導率的理論上限,與文獻[21]的結果310 W·m?1·K?1基本一致.

室溫下,100 nm長純12C聚乙烯單鏈的熱導率約為聚乙烯塊體熱導率的100倍,與金的熱導率317 W·m?1·K?1[8]相近.這說明聚乙烯材料的有序和晶體化使其導熱能力呈現了質的飛躍,在有機高熱導材料開發領域,聚乙烯將有廣闊的前景.

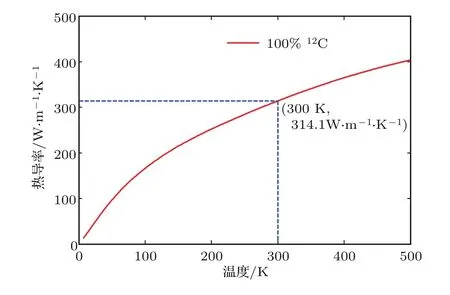
圖6 T=300 K時100 nm純12C聚乙烯單鏈的熱導率Fig.6.Thermal conductivity of pure12C polyethylene chain with a length of 100 nm at 300 K.

室溫300 K條件下,12C聚乙烯單鏈依次提高13C或14C的摻雜濃度時,體系的平均熱導先變小,后變大,最后與初始平均熱導相近,如圖7所示.該變化趨勢與石墨烯帶及硅納米線熱輸運的同位素效應規律相似[17,50,51].從圖中可以看出,相同摻雜比例下,14C元素熱導的同位素效應比13C元素更為顯著.聚乙烯單鏈12C,13C熱導的同位素效應在等比例摻雜時最為突出,平均熱導比純凈的12C聚乙烯單鏈降低了33%;同樣,聚乙烯單鏈12C,14C熱導的同位素效應也在等比例摻雜時最為突出,平均熱導比未摻雜時降低了51%.由此可見,其他條件一定時,聚乙烯單鏈同位素效應在等比例隨機摻雜時聲子散射最強烈,此時單、多道散射并存,呈現整體散射行為,體系的平均熱導出現最小值.

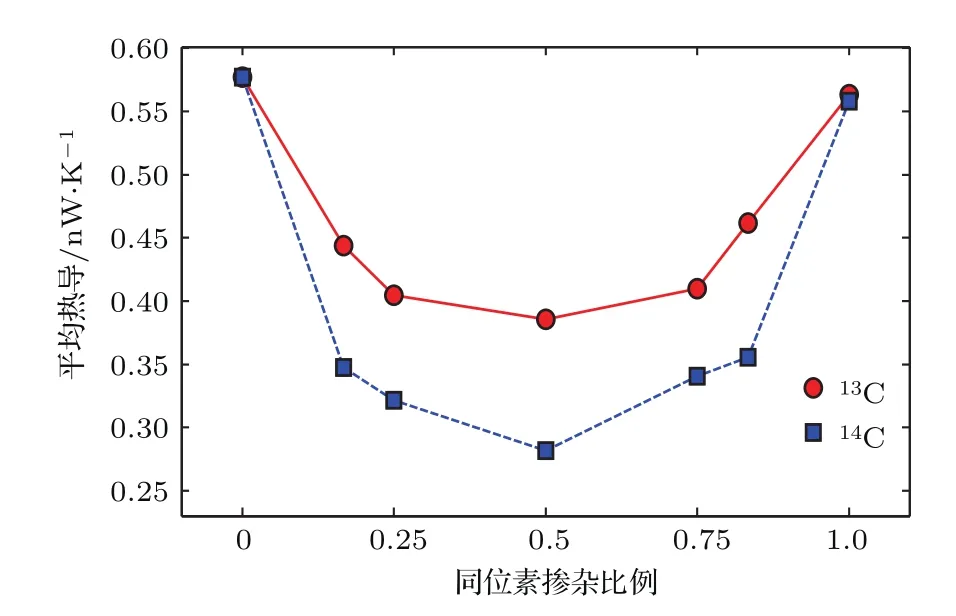
圖7 T=300 K時12C聚乙烯單鏈分別摻入不同比例13C,14C雜質的平均熱導Fig.7.Average thermal conductance of isotope-doped polyethylene chains with various13C and14C ratios at 300 K.

聚乙烯熱導的同位素效應可作為熱導調節的一種實現方式.從傳熱角度考慮,可通過降低同位素雜質含量的方法,提高聚乙烯的熱導率,這對設計聚乙烯高熱導材料、有機太陽能電池之類的納米電子器件頗為重要.

4 結論

我們應用DFT,CIS和NEGF方法計算了室溫下100 nm長純12C聚乙烯單鏈的熱導率的理論上限,并在第一性原理精度上對聚乙烯單鏈在各同位素摻雜比例下,聲子單、多道散射共存的一般情形進行了研究,克服了級聯散射模型和標度理論只能處理低摻雜濃度(6 10%)的不足.計算發現,對于純12C聚乙烯單鏈體系,13C或14C雜質引起的熱導同位素效應都在摻雜原子百分數為50%時最為顯著.這為認知聚乙烯材料導熱性能的同位素影響提供了理論依據.

感謝中國人民大學物理系2011年暑期舉辦的量子輸運理論和納米電子學模擬國際研討會暨第一屆量子輸運模擬講習班,以及那個炎夏揮汗付出的各位老師、同學,特別是不辭萬里辛勞專程趕來的郭鴻老師,朱煜、胡亦斌博士.另外,感謝南京師范大學趙玄機博士的深度討論和大力幫助.

[1]Reecht G,Scheurer F,Speisser V,Dappe Y J,Mathevet F,Schull G 2014 Phys.Rev.Lett.112 047403

[2]Singh V,Bougher T L,Weathers A,Singh V,Bougher T,Weathers A,Cai Y,Bi K,Pettes M T,McMenamin S A,Lv W,Resler D P,Gattuso T R,Altman D H,Sandhage K H,Shi L,Henry A,Cola B A 2014 Nature Nanotech.9 384

[3]Henry A,Chen G 2008 Phys.Rev.Lett.101 235502

[4]Shen S,Henry A,Tong J,Zheng R T,Chen G 2010 Nature Nanotech.10 1038

[5]Cao B Y,Dong R Y,Kong J,Chen H,Xu Y,Rong Q L,Cai A 2012 Acta Phys.Sin.61 046501(in Chinese)[曹炳陽,董若宇,孔杰,陳恒,徐雁,容啟亮,蔡岸2012物理學報61 046501]

[6]Yamanaka A,Takao T 2011 ISRN Mater.Sci.10 5402

[7]Liao Q W,Liu Z C,Liu W,Deng C C,Yang N 2015 Sci.Rep.5 16543

[8]Stocker H 2004 Physics Manual(Beijing:Peking University Press)p700(in Chinese)[斯托克2004物理手冊(北京:北京大學出版社)第700頁]

[9]Onn D G,Witek A,Qiu Y Z,Anthony T R,Banholzer W F 1992 Phys.Rev.Lett.68 2806

[10]Xu Y,Chen X B,Gu B L,Duan W H 2009 Appl.Phys.Lett.95 233116

[11]Xie Z X,Tang L M,Pan C N,Li K M,Chen K Q,Duan W H 2012 Appl.Phys.Lett.100 073105

[12]Xie Z X,Chen K Q,Duan W H 2011 Phys.Condens.Matter.23 315302

[13]Si C,Liu Z,Duan W H,Liu F 2013 Phys.Rev.Lett.111 196802

[14]Tan Z W,Wang J S,Chee K G 2011 Nano Lett.11 214

[15]Zhang H J,Lee G,Fonseca A F,Borders T L,Cho K 2010 J.Nanomater.7 537657

[16]Sevin?li H,Sevik C,?a?n T,Cuniberti G 2013 Nature.Sci.Rep.3 1228

[17]Chen S S,Wu Q Z,Mishra C,Kang J Y,Zhang H J,Cho K,Cai W W,Balandin A A,Ruo ffR S 2012 Nature Mater.10 1038

[18]Henry A,Chen G 2009 Phys.Rev.B 79 144305

[19]Hu G J,Cao B Y,Li Y W 2014 Chin.Phys.Lett.31 086501

[20]Li X Q,Chen J,Yu C X,Zhang G 2013 Appl.Phys.Lett.103 013111

[21]Jiang J W,Zhao J H,Zhou K,Rabczuk T 2012 J.Appl.Phys.111 124304

[22]Chen X B,Duan W H 2015 Acta Phys.Sin.64 186302(in Chinese)[陳曉彬,段文暉2015物理學報64 186302]

[23]Gao B,Jiang J,Liu K,Wu Z Y,Lu W,Luo Y 2007 J.Comput.Chem.29 434

[24]Jiang J,Liu K,Lu W,Luo Y 2006 J.Chem.Phys.124 214711

[25]Taylor J,Guo H,Wang J 2001 Phys.Rev.B 63 245407

[26]Wang J S,Wang J,Lü J T 2008 Eur.Phys.J.B 62 381

[27]Hou Q W,Cao B Y,Guo Z Y 2009 Acta Phys.Sin.58 7809(in Chinese)[侯泉文,曹炳陽,過增元2009物理學報58 7809]

[28]Hua Y C,Dong Y,Cao B Y 2013 Acta Phys.Sin.62 244401(in Chinese)[華鈺超,董源,曹炳陽2013物理學報62 244401]

[29]Jia X F,Du L,Tang D H,Wang T L,Chen W H 2012 Acta Phys.Sin.61 127202(in Chinese)[賈曉菲,杜磊,唐冬和,王婷嵐,陳文豪2012物理學報61 127202]

[30]Gu Y F,Wu X L,Wu H Z 2016 Acta Phys.Sin.65 248104(in Chinese)[顧云風,吳曉莉,吳宏章2016物理學報65 248104]

[31]Yamamoto T,Watanabe S,Watanabe K 2004 Phys.Rev.Lett.92 075502

[32]Mingo N,Yang L 2003 Phys.Rev.B 68 245406

[33]Frisch M J,Trucks G W,Schlegel H B,et al.2009 Gaussian 09 Revision A.02,Gaussian,Inc.,Wallingford CT

[34]Mingo N,Stewart D A,Broido D A,Srivastava D 2008 Phys.Rev.B 77 033418

[35]Nikoli? B K,Saha K K,Markussen T,Thygesen K S 2012 J.Comput.Electron.11 78

[36]Hu W P,Jiang J,Nakashima H,Luo Y,Kashimura Y,Chen K Q,Shuai Z,Furukawa K,Lu W,Liu Y Q,Zhu D B,Torimitsu K 2006 Phys.Rev.Lett.96 027801

[37]Jiang J,Gao B,Han T T,Fu Y 2009 Appl.Phys.Lett.94 092110

[38]Jiang J,Sun L,Gao B,Wu Z Y,Lu W,Yang J L,Luo Y 2010 J.Appl.Phys.108 094303

[39]NISTComputationalChemistryComparisonand Benchmark Database http://cccbdb.nist.gov/vibscalejust.asp

[40]Datta S,Cahay M,McLennan M 1987 Phys.Rev.B 36 5655

[41]Savic I,Mingo N,Stewart D A 2008 Phys.Rev.Lett.101 165502

[42]Stewart D A,Savic I,Mingo N 2009 Nano Lett.9 81

[43]Markussen T,Jauho A P,Brandbyge M 2009 Phys.Rev.B 79 035415

[44]Markussen T,Rurali R,Jauho A P,Brandbyge M 2007 Phys.Rev.Lett.99 076803

[45]Calzolari A,Jayasekera T,Kim K W,Nardelli M B 2012 J.Phys.Condens.Matter 24 492204

[46]Yamamoto T,Watanabe K 2006 Phys.Rev.Lett.96 255503

[47]Zavgorodnev Y V,Chvalun S N,Nikolaeva G Y,Sagitova E A,Pashinin P,Gordeyev S A,Prokhorov K A 2015 J.Phys.Conf.Ser.594 012010

[48]Ghosh S,Calizo I,Teweldebrhan D,Pokatilov E P,Nika D L,Balandin A A,Bao W,Miao F,Lau C N 2008 Appl.Phys.Lett.92 151911

[49]Smith P,Chanzy H D,Rotzinger B P 1987 J.Mater.Sci.22 523

[50]Jiang J W,Lan J H,Wang J S,Li B W 2010 J.Appl.Phys.107 054314

[51]Yang N,Zhang G,Li B W 2008 Nano Lett.8 276

PACS:65.80.–g,66.30.hk,61.41.+eDOI:10.7498/aps.66.116501

Isotope e ff ect on quantum thermal transport in a polyethylene chain?

Wu Yu1)2)Cai Shao-Hong1)3)?Deng Ming-Sen3)4)Sun Guang-Yu2)Liu Wen-Jiang1)3)Cen Chao2)
1)(College of Big Data and Information Engineering,Guizhou University,Guiyang 550025,China)
2)(School of Physics and Electronic Science,Institute of Applied Physics,Guizhou Normal University,Guiyang 550018,China)
3)(Guizhou Provincial Key Laboratory of Economic System Simulation,Guizhou University of Finance and Economics,Guiyang 550025,China)
4)(Guizhou Provincial Key Laboratory of Computational Nano-Material Science,Guizhou Normal University,Guiyang 550018,China)

20 January 2017;revised manuscript

27 March 2017)

E ff ective control of thermal conductive property of polymeric materials is now attracting more and more attention from both the theoretical and the experimental aspects.Bulk polyethylene is regarded as a thermal insulator because its thermal conductivity is typically on the order of 0.35 W·m?1·K?1.However,recent studies demonstrate that a polyethylene chain has an extremely high thermal conductivity and the reported thermal conductivity of ultra-drawn polyethylene nano fi bers is as high as 104 W·m?1·K?1,about 300 times higher than that of bulk polyethylene.In order to cast o ffthis dilemma,several simulation methods are used to detect the unusually high thermal conductivity of a polyethylene chain.Molecular dynamics(MD)simulation results are highly sensitive to the choice of empirical potential or simulation method.Even using the same potential(AIREBO potential),the obtained thermal conductivity of a polyethylene chain is di ff erent.By combining the Green-Kubo method with a modal decomposition approach,equilibrium molecular dynamics(EMD)indicates that the thermal conductivity is able to exceed 100 W·m?1·K?1while the polyethylene chain is longer than 40 nm at room temperature.Compared with the simulation result obtained by equilibrium molecular dynamics,the simulation result provided by using the non-equilibrium molecular dynamics(NEMD)method is only 57 W·m?1·K?1for a 160-nm-long polyethylene chain at room temperature.We use the fi rst-principles method to calculate the force constant tensor,and the characteristics of quantum thermal transport in a polyethylene chain can be revealed.In our algorithm,several shortcomings of molecular dynamics,i.e.,di ff erent potential functions or simulation methods may lead to obviously di ff erent results for the same quantum thermal transport system,are overcome.Based on the density functional theory(DFT),the central insertion scheme(CIS)combined with nonequilibrium Green’s function(NEGF)is used to evaluate the isotope e ff ect on quantum thermal transport in a polyethylene chain,which includes 432 atoms in scattering region and has a length of 18.533 nm.It is found that the upper limit of thermal conductivity of a 100-nm-long pure12C polyethylene chain reaches a high value of 314.1 W·m?1·K?1at room temperature.Moreover,for the case of a pure polyethylene chain of12C,with other conditions unchanged,the reduction of average thermal conductance caused by14C impurity is more remarkable than that by13C.The most outstanding isotope e ff ect on quantum thermal transport can be detected in the polyethylene chain.When the doping concentration of14C in12C is 50%at room temperature,the average thermal conductance will be reduced by 51%.It is of great signi fi cance for studying the mechanism of isotope e ff ect on thermal transport in polyethylene.

polyethylene chains,quantum thermal transport,average thermal conductance,isotope e ff ect

10.7498/aps.66.116501

?國家自然科學基金(批準號:11264005)、貴州省科學技術基金(批準號:黔科合J字[2012]2292號)、貴州省教育廳自然科學研究項

目(批準號:黔教合KY字[2014]307,黔教科2008057,2007036)資助的課題.

?通信作者.E-mail:caish@mail.gufe.edu.cn

?2017中國物理學會Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.11264005),the Foundation of Science and Technology of Guizhou Province,China(Grant No.J[2012]2292),and the Natural Science Foundation of the Education Department of Guizhou Province,China(Grant Nos.[2014]307,2008057,2007036).

?Corresponding author.E-mail:caish@mail.gufe.edu.cn