含時(shí)驅(qū)動(dòng)的Dicke模型的混沌特性?
劉妮梁九卿
(山西大學(xué)理論物理研究所,太原 030006)
含時(shí)驅(qū)動(dòng)的Dicke模型的混沌特性?
劉妮?梁九卿
(山西大學(xué)理論物理研究所,太原 030006)
(2017年1月21日收到;2017年3月28日收到修改稿)
依據(jù)Dicke量子相變首次被觀測(cè)的實(shí)驗(yàn)裝置,我們通過調(diào)節(jié)抽運(yùn)激光強(qiáng)度來實(shí)現(xiàn)原子-場(chǎng)集體耦合強(qiáng)度的單頻非絕熱調(diào)制,即實(shí)現(xiàn)含時(shí)驅(qū)動(dòng)的Dicke模型.當(dāng)驅(qū)動(dòng)的耦合強(qiáng)度為零時(shí),系統(tǒng)回退到標(biāo)準(zhǔn)的Dicke模型.從刻畫的龐加萊截面圖觀測(cè)到:在臨近相變點(diǎn)附近系統(tǒng)由經(jīng)典規(guī)則軌道向混沌變化,超輻射區(qū)對(duì)應(yīng)著相空間的完全混沌;當(dāng)靜態(tài)耦合和驅(qū)動(dòng)耦合同時(shí)存在時(shí),系統(tǒng)顯示出豐富的混沌運(yùn)動(dòng).通過調(diào)節(jié)振蕩頻率,系統(tǒng)可在正常相區(qū)間從經(jīng)典規(guī)則軌道變到混沌再變到經(jīng)典規(guī)則軌道.
單頻非絕熱調(diào)制,Dicke模型,量子混沌,龐加萊截面圖
1 引言
很多量子系統(tǒng)都存在量子混沌,量子混沌是一種普遍存在的現(xiàn)象,它與相變、糾纏、隧穿等物理現(xiàn)象存在很多關(guān)聯(lián).經(jīng)典哈密頓系統(tǒng)是否可積與混沌直接相關(guān).把經(jīng)典力學(xué)中的可積性推廣到量子力學(xué)對(duì)量子混沌的研究是非常有益的.現(xiàn)在人們經(jīng)常使用的量子可積性定義都是經(jīng)典可積性的推廣.三十多年前,科學(xué)家已經(jīng)預(yù)測(cè)到標(biāo)準(zhǔn)Dicke模型存在正常相到超輻射相的量子相變[1?3].同時(shí),Dicke模型的量子混沌特性也早有研究[4?8],但是真正將其混沌特性與量子相變連接在一起的卻是從文獻(xiàn)[9]開始的.文獻(xiàn)[9]指出:標(biāo)準(zhǔn)Dicke模型會(huì)經(jīng)歷從準(zhǔn)可積到量子混沌的變化,而且這種變化是由與之完全對(duì)應(yīng)的量子相變引起的.我們考慮一組四能級(jí)原子自發(fā)地與橫向抽運(yùn)激光驅(qū)動(dòng)的單模腔場(chǎng)進(jìn)行相互作用的系統(tǒng).最近,實(shí)驗(yàn)上已在玻色-愛因斯坦凝聚(BEC)與高精細(xì)光腔組合的實(shí)驗(yàn)中實(shí)現(xiàn)了相似的裝置,而且在該裝置中觀測(cè)到了從正常相到超輻射相的Dicke量子相變[10].該裝置的一個(gè)直觀優(yōu)點(diǎn)是:通過操縱抽運(yùn)激光強(qiáng)度來實(shí)現(xiàn)可調(diào)諧的集體原子場(chǎng)耦合強(qiáng)度.本文的主要想法是:在實(shí)現(xiàn)的Dicke模型中引入含時(shí)依賴的原子場(chǎng)集體耦合項(xiàng).我們發(fā)現(xiàn):當(dāng)含時(shí)系統(tǒng)回退到標(biāo)準(zhǔn)Dicke模型時(shí),其量子混沌特性與前人的結(jié)果完全符合,在臨界相變點(diǎn)附近發(fā)生從規(guī)則周期軌道到完全混沌的變化.當(dāng)我們引入原子場(chǎng)集體耦合強(qiáng)度的單頻非絕熱調(diào)制項(xiàng)后,系統(tǒng)的混沌特性變得非常復(fù)雜.為了更好地理解靜態(tài)耦合(?g=0)和驅(qū)動(dòng)耦合(?=0),以及弱驅(qū)動(dòng)(如:?g=0.2)和強(qiáng)驅(qū)動(dòng)(如:?g=0.6)對(duì)含時(shí)Dicke系統(tǒng)混沌特性的影響,本文給出了一系列參數(shù)下系統(tǒng)的龐加萊截面圖,為研究含時(shí)Dicke系統(tǒng)提供了一種新的研究方法和研究手段.結(jié)果發(fā)現(xiàn)只有系統(tǒng)整體穩(wěn)定,局部不穩(wěn)定才會(huì)出現(xiàn)混沌.
2 含時(shí)驅(qū)動(dòng)的Dicke模型
2.1 理論模型
Dicke模型描述單個(gè)二能級(jí)原子系綜集體耦合到一個(gè)單模量子化電磁場(chǎng)的情形,當(dāng)原子-場(chǎng)集體耦合強(qiáng)度超過某個(gè)臨界值時(shí)系統(tǒng)會(huì)經(jīng)歷一個(gè)零溫量子相變,發(fā)生從正常相到超輻射相的量子相變.該相變已于2010年由Baumann等首次在實(shí)驗(yàn)上觀測(cè)到[10].這種集體量子現(xiàn)象所引起的超輻射-正常量子相變?cè)谠游锢砗土孔庸鈱W(xué)中被廣泛研究.此外量子混沌、基態(tài)糾纏、臨界行為等與量子相變相關(guān)的領(lǐng)域也為大家所關(guān)注.依據(jù)Baumann等[10]提出的實(shí)驗(yàn)裝置(即一組Rb87的四能級(jí)超冷原子與單模光場(chǎng)發(fā)生集體相互作用,外加橫向抽運(yùn)激光),每個(gè)原子有兩個(gè)穩(wěn)定的基態(tài),分別記為|0,0?和|±kpmk?,它們通過兩束拉曼通道耦合.在大失諧極限下,原子的激發(fā)態(tài)能被絕熱消除而成為有效的二能級(jí)系統(tǒng)[11?13],運(yùn)用集體自旋算符Si(i=±,z)來表示,這樣我們實(shí)現(xiàn)了Dicke類型的哈密頓量(~=1):
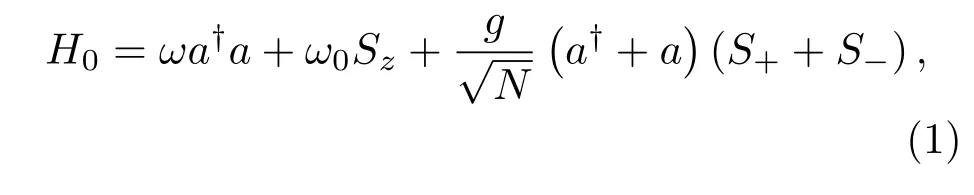
其中,N是原子數(shù);有效腔頻ω=ωc?ωp,而ωc是腔頻,ωp是橫向抽運(yùn)激光頻率;有效原子頻率ω0=2ωr,而原子的反沖能量ωr=k2/2m;集體耦合強(qiáng)度,而ξ是抽運(yùn)拉比頻率;a?和a代表光子的產(chǎn)生和湮沒算符;集體原子算符Si(i=±,z)滿足SU(2)角動(dòng)量關(guān)系.
實(shí)驗(yàn)上通過改變抽運(yùn)激光強(qiáng)度來調(diào)節(jié)橫向抽運(yùn)激光頻率ωp,進(jìn)而調(diào)節(jié)集體原子-場(chǎng)耦合強(qiáng)度.那么將原子-場(chǎng)耦合強(qiáng)度調(diào)制成g(t)=g+?g cos(ηt)這樣的形式,我們將得到含時(shí)驅(qū)動(dòng)的Dicke模型[14,15],即
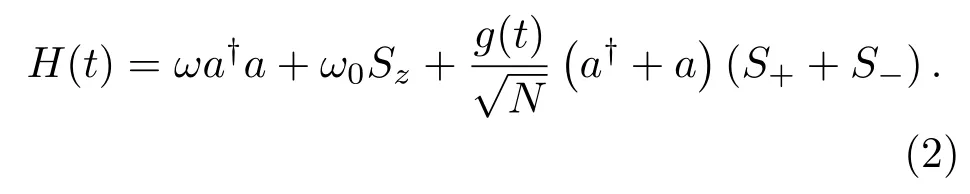
哈密頓量(2)與哈密頓量(1)具有相同的形式,只是原子-場(chǎng)耦合強(qiáng)度g被取代為g(t).g(t)的最大值和最小值分別為g+?g和g??g.在后面我們會(huì)發(fā)現(xiàn):規(guī)則軌道到量子混沌的臨界點(diǎn)并非僅僅由g+?g和g??g體現(xiàn),這是不同于標(biāo)準(zhǔn)Dicke模型的混沌特性的.在熱力學(xué)極限,N→∞,無驅(qū)動(dòng)的Dicke模型(?g=0)在臨界耦合時(shí)顯示一個(gè)量子相變,此時(shí)基態(tài)從無激發(fā)的正常相變到對(duì)稱破缺的超輻射相.在超輻射相區(qū),場(chǎng)和原子集體都具有了宏觀占據(jù).同時(shí)混沌特性也正是在相變點(diǎn)處從規(guī)則軌道變化到完全的混沌.我們通過調(diào)查無驅(qū)動(dòng)下Dicke模型的龐加萊截面圖來開始我們的分析.
我們先使用Holstein-Primako ff變換[16,17],即用單一玻色模取代自旋算符的操作:
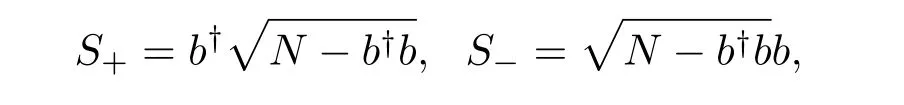

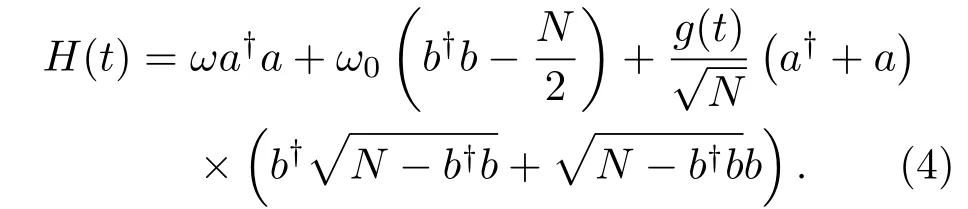
標(biāo)準(zhǔn)Dicke模型可以演化出許多不同的半經(jīng)典模型[5],而且也發(fā)展了許多不同的研究方法.廣泛討論的方法是Hartree-Fork-type的近似,它是先得到系統(tǒng)的海森伯運(yùn)動(dòng)方程,并用期待值取代方程中的算符[4].它們被看作經(jīng)典變量,并且得到它們的一系列非線性運(yùn)動(dòng)方程.依據(jù)這些運(yùn)動(dòng)方程可以得到一定參數(shù)區(qū)的經(jīng)典混沌.盡管如此,在一定程度上,上面的方法并不能完全滿足僅依賴于原子數(shù)N變化的運(yùn)動(dòng).Furuya等[5]研究了類似于Dicke模型的一個(gè)經(jīng)典模型,通過在光子和原子相干態(tài)基失構(gòu)成的態(tài)下評(píng)定系統(tǒng)的期待值,得到其半經(jīng)典哈密頓量,并且展示出系統(tǒng)出現(xiàn)混沌.盡管文獻(xiàn)中的模型與我們的無驅(qū)動(dòng)Dicke模型非常相似,但其并未完備地討論模型的混沌特性.而混沌特性是反映系統(tǒng)諸如量子相變、穩(wěn)定性等基態(tài)特性至關(guān)重要的手段或特征.
2.2 運(yùn)動(dòng)方程
通過引入兩玻色模的坐標(biāo)和位置算符關(guān)系,即兩維諧振子算符與坐標(biāo)和位置的關(guān)系
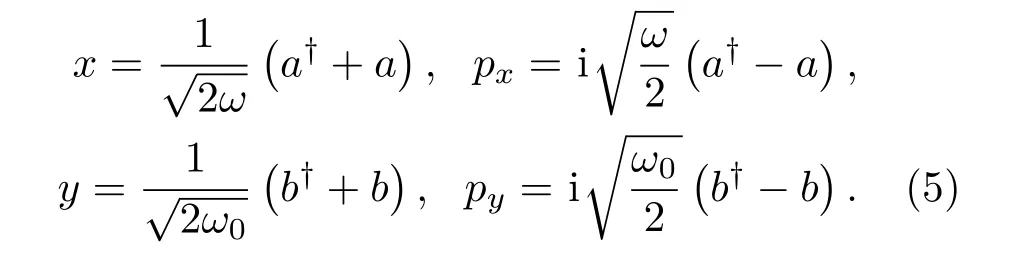
將(5)式經(jīng)過整理得到
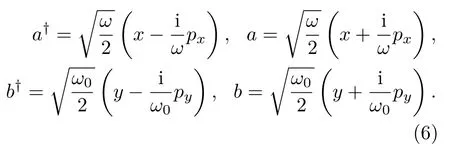
將(6)式坐標(biāo)-動(dòng)量表示代入哈密頓量(4),得到如下形式的系統(tǒng)經(jīng)典哈密頓量:
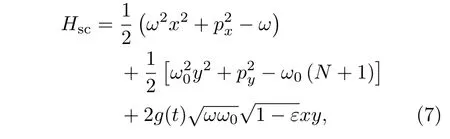
為了分析有限粒子數(shù)N的半經(jīng)典系統(tǒng)的行為,我們從Hsc的偏導(dǎo)數(shù)給出了哈密頓量的運(yùn)動(dòng)方程:
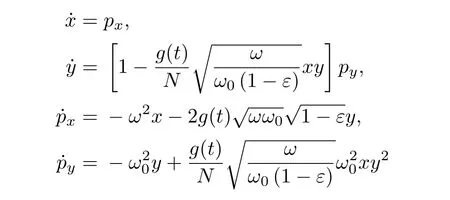
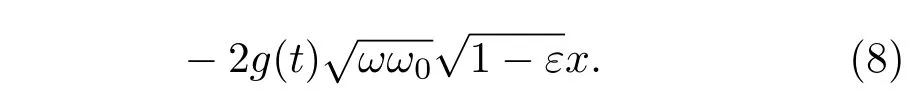
3 系統(tǒng)的混沌特性
原則上由經(jīng)典哈密頓量和運(yùn)動(dòng)方程就可以研究系統(tǒng)的混沌特性.我們?cè)诔跏紬l件和各種變化參數(shù)下數(shù)值地調(diào)研了半經(jīng)典系統(tǒng)的哈密頓量運(yùn)動(dòng)方程.為了分析系統(tǒng)的運(yùn)動(dòng)軌跡,我們使用四維相空間的龐加萊截面圖來刻畫.我們定義截面圖的表面為x=0,px由E(t)確定.作為例證,圖1給出了某參數(shù)下的無驅(qū)動(dòng)Dicke系統(tǒng)的(y,py)平面的龐加萊截面圖.

圖1 無驅(qū)動(dòng)Dicke模型隨參數(shù)變化的龐加萊截面圖,其中初始能量E=20,原子數(shù)N=1000,哈密頓量在共振情形ω=ω0=1Fig.1.The Poincaré sections of the undriven Dicke model in the resonance case of ω=ω0=1.The plotted parameters are given by the initial energy E=20 and the atomic number N=1000.
圖1清晰地描述出:在原子-場(chǎng)耦合強(qiáng)度g很小,即g 6 0.4(如圖1(a),(b))時(shí),龐加萊截面圖是由一系列規(guī)則、周期或準(zhǔn)周期軌道組成;接近臨界原子-場(chǎng)耦合強(qiáng)度,即g=0.44,g=0.50(如圖1(c),(d))時(shí),我們看到周期軌道特征的改變,并且出現(xiàn)許多混沌軌跡,即軟混沌;增加原子-場(chǎng)耦合強(qiáng)度更導(dǎo)致殘余的周期軌道解體,并且整個(gè)相空間變成混沌區(qū),即硬混沌,如原子-場(chǎng)耦合強(qiáng)度略微超過臨界值gc=0.50,即g=0.52,g=0.60(如圖1(e),(f)).該圖結(jié)果再一次驗(yàn)證了文獻(xiàn)[9]中圖14的結(jié)果,也表明無論從理論計(jì)算還是數(shù)值模擬,無驅(qū)動(dòng)結(jié)果回退的正確性,這也保證了我們后面給出驅(qū)動(dòng)Dicke模型結(jié)論的可靠性.最重要的是,圖1表明:對(duì)于標(biāo)準(zhǔn)Dicke模型,量子相變點(diǎn)是系統(tǒng)由規(guī)則軌道向混沌轉(zhuǎn)變的指標(biāo).
圖2清晰地展示出,當(dāng)靜態(tài)耦合不存在時(shí),系統(tǒng)是沒有混沌特性的.驅(qū)動(dòng)耦合的調(diào)節(jié)本質(zhì)上并沒有改變系統(tǒng)的物理特性.該組圖告訴我們,此時(shí)的原子-場(chǎng)耦合強(qiáng)度本質(zhì)上是由余旋函數(shù)?g cos(?t)調(diào)節(jié)的振蕩形式,且原子-場(chǎng)耦合強(qiáng)度取最大值g(t)max=0,0.4,0.6,0.8時(shí),并沒有顯示出規(guī)則軌道或混沌圖像.可見,混沌圖像是與我們的靜態(tài)耦合g息息相關(guān)的.
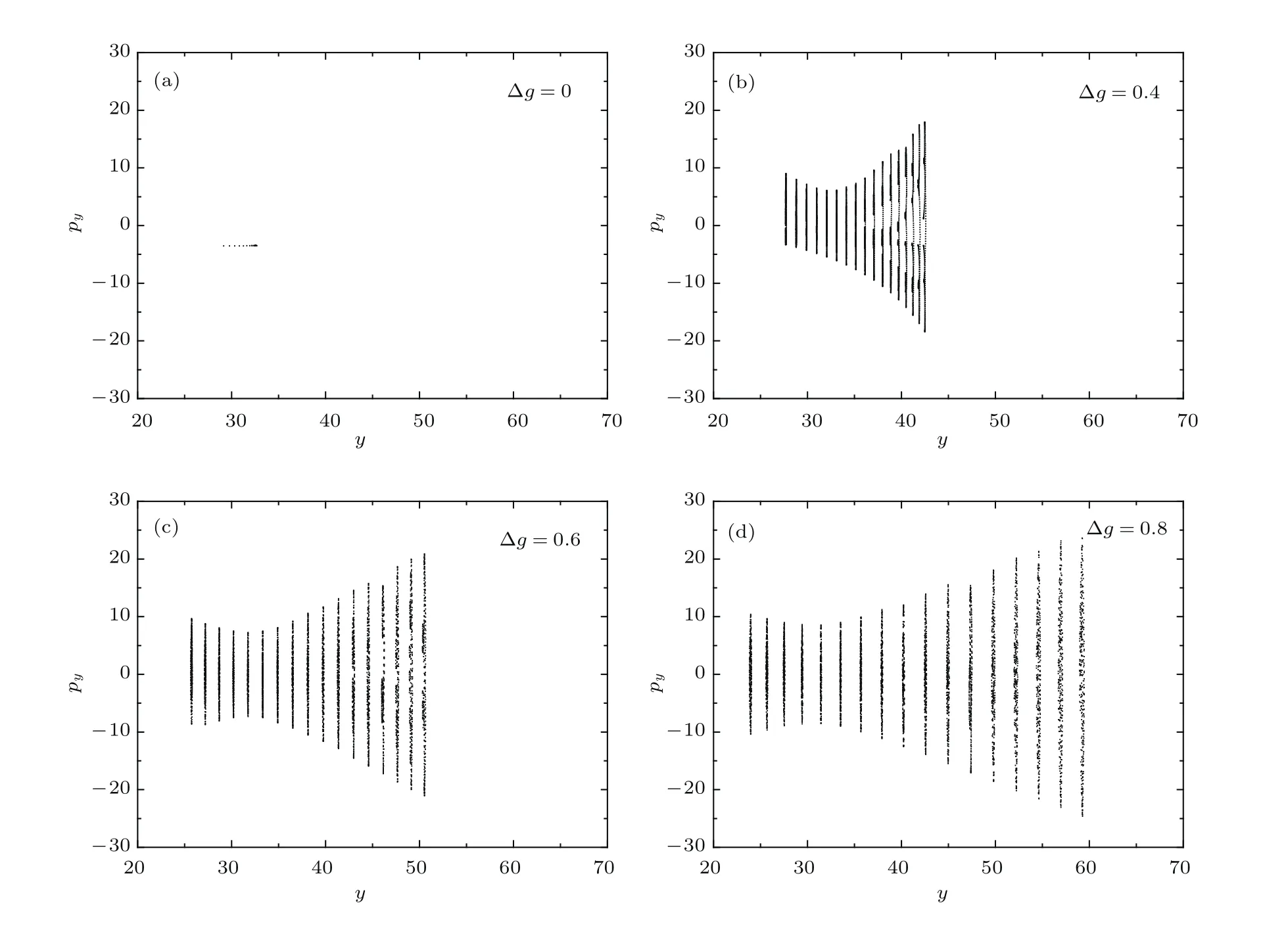
圖2 靜態(tài)耦合為零(g=0),驅(qū)動(dòng)耦合變化(?=0)時(shí)Dicke模型的龐加萊截面圖,其中初始能量E=20,原子數(shù)N=1000,振蕩頻率?=10,且哈密頓量在共振情形ω=ω0=1Fig.2.The Poincaré sections of Dicke model as the function of the driven coupling strength?g with the static coupling g=0 in the resonance case of ω=ω0=1.The plotted parameters are given by the initial energy E=20,the atomic number N=1000,and the oscillation frequency ?=10.
圖4主要展示的是不同靜態(tài)耦合和驅(qū)動(dòng)耦合下系統(tǒng)的龐加萊截面圖.由圖4(a)可以看出,當(dāng)靜態(tài)耦合g=0.2
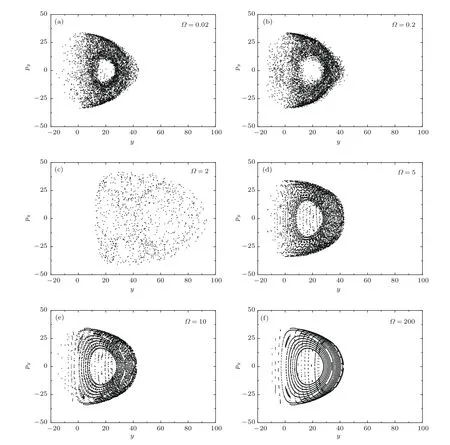
圖3 靜態(tài)耦合和驅(qū)動(dòng)耦合為定值(g=?g=0.2)時(shí)含時(shí)Dicke模型隨振蕩頻率變化的龐加萊截面圖,其中初始能量E=20,原子數(shù)N=1000,振蕩頻率?=0.02,0.2,2,5,10,200,且哈密頓量是在共振情形ω=ω0=1Fig.3.The Poincaré sections of the driven Dicke model with time-dependent as a function of the oscillation frequency ? with the given coupling g=?g=0.2 in the resonance case of ω=ω0=1.The plotted parameters are given by the initial energy E=20 and the atomic number N=1000.
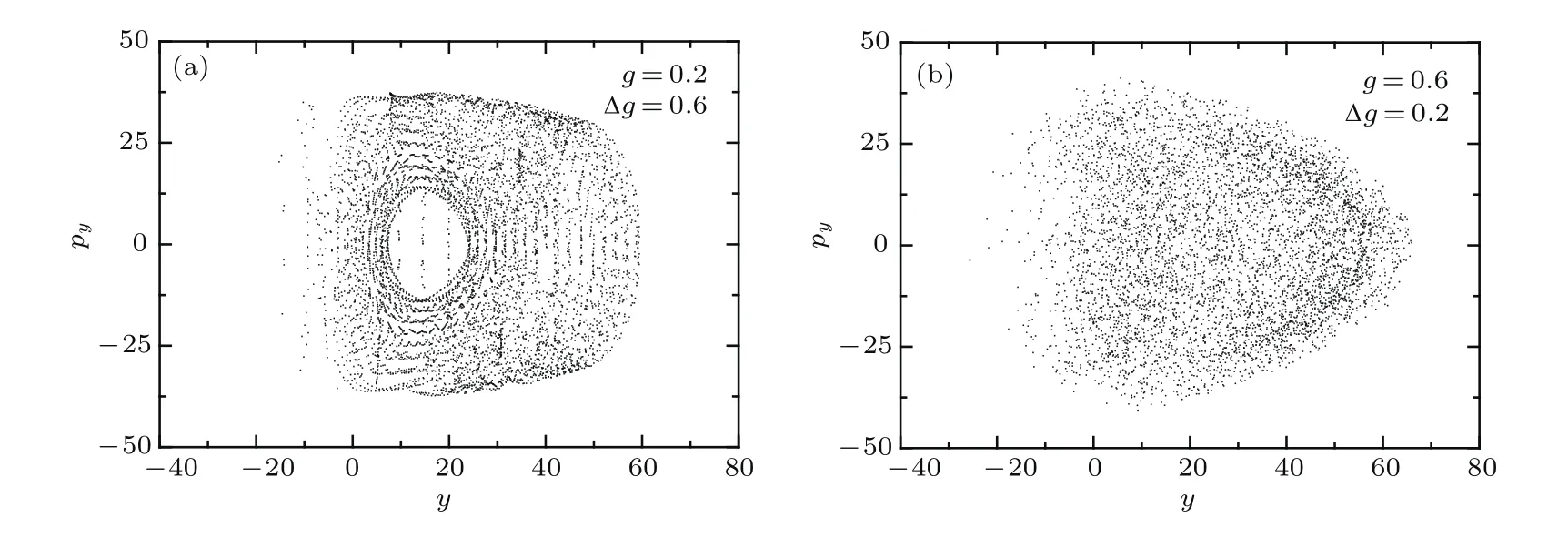
圖4 靜態(tài)耦合和驅(qū)動(dòng)耦合影響下含時(shí)Dicke模型的龐加萊截面圖,其中初始能量E=20,原子數(shù)N=1000,振蕩頻率?=10,且哈密頓量是在共振情形ω=ω0=1Fig.4.The Poincaré sections of the driven Dicke model with time-dependent as the function of the static and driven coupling strengths in the resonance case of ω=ω0=1.The plotted parameters are given by the initial energy E=20,the atomic number N=1000 and the oscillation frequency ?=10.

圖5 給定的靜態(tài)耦合(g=0.6)下變化的驅(qū)動(dòng)耦合對(duì)含時(shí)Dicke模型龐加萊截面圖的影響,其中初始能量E=20,原子數(shù)N=1000,振蕩頻率?=10,且哈密頓量是共振情形ω=ω0=1Fig.5.The Poincaré sections of the driven Dicke model with time-dependent as a function of the driven coupling strength with the given static coupling strength g=0.6 in the resonance case of ω=ω0=1.The plotted parameters are given by the initial energy E=20,the atomic number N=1000 and the oscillation frequency ?=10.
為了更好地說明驅(qū)動(dòng)耦合?g對(duì)系統(tǒng)是否出現(xiàn)混沌的調(diào)節(jié)作用,圖5給出了靜態(tài)耦合為g=0.6時(shí),不同驅(qū)動(dòng)耦合下系統(tǒng)的龐加萊截面圖.圖5(a)說明當(dāng)靜態(tài)耦合g=0.6>gc=0.5時(shí),調(diào)節(jié)驅(qū)動(dòng)耦合?g=0.2系統(tǒng)顯示的是完全混沌圖像,與無驅(qū)動(dòng)情形完全一致,參看圖1(f);若調(diào)節(jié)驅(qū)動(dòng)耦合?g=2.0,系統(tǒng)仍然顯示的是完全混沌圖像,但在中間區(qū)域出現(xiàn)一個(gè)很小的半月形區(qū)域,如圖5(b);隨著驅(qū)動(dòng)耦合?g增大,在整個(gè)混沌空間內(nèi),中間區(qū)域越來越大,且越來越趨于規(guī)則圖像,參見圖5(c),(d);當(dāng)驅(qū)動(dòng)耦合?g增大至5.0時(shí),整個(gè)區(qū)間變成規(guī)則圖像,系統(tǒng)顯示的是規(guī)則周期軌道.可見,靜態(tài)耦合g可以調(diào)節(jié)出混沌特性,但同時(shí)驅(qū)動(dòng)耦合?g也可以使系統(tǒng)顯示混沌特性向規(guī)則周期軌道轉(zhuǎn)變.由此看來,含時(shí)系統(tǒng)的混沌特性要復(fù)雜于理想系統(tǒng),而且含時(shí)規(guī)律的不同直接影響混沌圖.
4 結(jié)論
本文考慮了包含單頻非絕熱調(diào)制的原子-場(chǎng)耦合強(qiáng)度的Dicke模型的混沌特性.在經(jīng)典系統(tǒng)從周期軌道到混沌變化可以反映出系統(tǒng)的量子特性,尤其量子相變點(diǎn)是我們分析規(guī)則軌道和混沌轉(zhuǎn)變的一個(gè)關(guān)鍵位置.如果僅有驅(qū)動(dòng)耦合系統(tǒng)是不會(huì)出現(xiàn)混沌圖像的,僅是振蕩形式的余弦函數(shù)的體現(xiàn);如果靜態(tài)耦合強(qiáng)度和驅(qū)動(dòng)耦合強(qiáng)度共存時(shí),系統(tǒng)的基態(tài)特性主要由靜態(tài)耦合決定,但驅(qū)動(dòng)耦合在一定程度上可以調(diào)節(jié)系統(tǒng)的軌道.當(dāng)系統(tǒng)的靜態(tài)耦合強(qiáng)度大于臨界耦合強(qiáng)度時(shí),龐加萊截面圖顯示系統(tǒng)是完全混沌圖像,但強(qiáng)的驅(qū)動(dòng)耦合也可以調(diào)節(jié)出規(guī)則軌道特性;當(dāng)系統(tǒng)的靜態(tài)耦合強(qiáng)度小于臨界耦合強(qiáng)度時(shí),通過調(diào)節(jié)驅(qū)動(dòng)耦合強(qiáng)度和振蕩頻率,系統(tǒng)也能顯示出混沌圖像.
[1]Hepp K,Lieb E H 1973 Ann.Phys.76 360
[2]Hioes F T 1973 Phys.Rev.A 8 1440
[3]Liu N,Lian J L,Ma J,Xiao L T,Chen G,Liang J Q,Jia S T 2011 Phys.Rev.A 83 033601
[4]Graham R,H?hnerbach M 1984 Phys.Lett.A 101 61
[5]Furuya K,Nemes M C,Pellegrino G Q 1998 Phys.Rev.Lett.80 5524
[6]Song L J,Yan D,Gai Y J,Wang Y B 2011 Acta Phys.Sin.60 020302(in Chinese)[宋立軍,嚴(yán)冬,蓋永杰,王玉波2011物理學(xué)報(bào)60 020302]
[7]Song L J,Yan D,Gai Y J,Wang Y B 2010 Acta Phys.Sin.59 3695(in Chinese)[宋立軍,嚴(yán)冬,蓋永杰,王玉波2010物理學(xué)報(bào)59 3695]
[8]Zhao W L,Wang J Z,Dou F Q 2012 Acta Phys.Sin.61 240302(in Chinese)[趙文壘,王建忠,豆福全2012物理學(xué)報(bào)61 240302]
[9]Emary C,Brandes T 2003 Phys.Rev.E 67 066203
[10]Baumann K,Guerlin C,Brennecke F,Esslinger T 2010 Nature 464 1301
[11]Yu L X,Fan J T,Zhu S Q,Chen G,Jia S T,Nori F 2014 Phys.Rev.A 89 023838
[12]Fan J T,Yang Z W,Zhang Y W,Ma J,Chen G,Jia S T 2014 Phys.Rev.A 89 023812
[13]Zhao X Q,Liu N,Liang J Q 2014 Phys.Rev.A 90 023622
[14]Bastidas V M,Emary C,Regler B,Brandes T 2012 Phys.Rev.Lett.108 043003
[15]Liu N,Li J D,Liang J Q 2013 Phys.Rev.A 87 053623
[16]Holstein T,Primako ffH 1949 Phys.Rev.A 58 1098
[17]Hillery M,Mlodinow L D 1984 Phys.Rev.A 31 797
PACS:05.45.Mt,42.50.Pq,73.43.NqDOI:10.7498/aps.66.110502
Chaos propeties of the time-dependent driven Dicke model?
Liu Ni?Liang Jiu-Qing
(Institute of Theoretical Physics,Shanxi University,Taiyuan 030006,China)
21 January 2017;revised manuscript
28 March 2017)
Now,many di ff erent approaches have been presented to study the di ff erent semi-classical models derived from the Dicke Hamiltonian,which re fl ect a fact that the quantum-mechanical spin possesses no direct classical analog.The Hartree-Fock-type approximation is one of the widely used approaches,with which we derive the Heisenberg equations of motion for the system and replace the operators in these equations with the corresponding expectation values.In the present paper,we investigate the role of quantum phase transition in determining the chaotic property of the timedependent driven Dicke model.The semi-classical Hamiltonian is derived by evaluating the expectation value of the Dicke Hamiltonian in a state,which is a product state of photonic and atomic coherent states.Based on the inverse of the relations between the position-momentum representation and the Bosonic creation-annihilation operators,the Hamiltonian is rewritten in the position-momentum representation and it undergoes a spontaneous symmetry-breaking phase transition,which is directly analogous to the quantum phase transition of the quantum system.In order to depict the Poincaré sections,which are used to analyze the trajectories through the four-dimensional phase space,we give the equations of motion of system from the derivatives of the semi-classical Hamiltonian for a variety of di ff erent parameters and initial conditions.According to the Dicke quantum phase transition observed from the experimental setup,we study the e ff ect of a monochromatic non-adiabatic modulation of the atom- fi eld coupling in Dicke model(i.e.,the driven Dicke model)on the system chaos by adjusting the pump laser intensity.The change from periodic track to chaotic fi gure re fl ects the quantum properties of the system,especially the quantum phase transition point,which is a key position for people to analyse the shift from periodic orbit to chaos.In an undriven case,the system reduces to the standard Dicke model.We discover from the Poincaré sections that the system undergoes a change from the classical periodic orbit to a number of chaotic trajectories and in the superradiant phase area,the whole phase space is completely chaotic.When the static and driving coupling both exist,the system shows rich chaotic motion.The ground state properties are mainly determined by the static coupling,while the orbit of the system is adjusted by the driving coupling.If the static coupling is greater than the critical coupling,the system displays completely chaotic images in the Poincaré sections,and the periodic orbits in the chaos can also be adjusted by the strong driving coupling.While the static coupling is less than the critical coupling,the system can also show the chaotic images by adjusting the driving coupling strength and oscillation frequency.Moreover,by tuning the oscillation frequency,the Poincaré sections may change from the classical orbits to the chaos,and back to the classical orbits in the normal phase of the system.
a monochromatic non-adiabatic modulation,Dicke model,quantum chaos,the Poincaré section
10.7498/aps.66.110502
?國家自然科學(xué)基金(批準(zhǔn)號(hào):11404198,11275118,91430109)、山西省高等學(xué)校科技創(chuàng)新項(xiàng)目(批準(zhǔn)號(hào):2014102)、山西大學(xué)科研啟動(dòng)金(批準(zhǔn)號(hào):011151801004)和國家基礎(chǔ)科學(xué)人才培養(yǎng)基金(批準(zhǔn)號(hào):J1103210)資助的課題.
?通信作者.E-mail:317446484@qq.com
?2017中國物理學(xué)會(huì)Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.11404198,11275118,91430109),the Scienti fi c and Technological Innovation Program of Higher Education Institutions in Shanxi Province(STIP),China(Grant No.2014102),the Launch of the Scienti fi c Research of Shanxi University,China(Grant No.011151801004),and the National Fundamental Training,China(Grant No.J1103210).
?Corresponding author.E-mail:317446484@qq.com

