壓裂車動力系統隔振優化研究

邱宗斌

(川慶鉆探工程公司 長慶井下技術作業公司，西安 710018)

壓裂車動力系統隔振優化研究

邱宗斌

(川慶鉆探工程公司 長慶井下技術作業公司，西安 710018)

針對石油壓裂車柴油發動機和壓裂泵等動力系統的振動問題，提出了一種隔振系統參數優化方法。該方法的優化目標為提高柴油發動機和壓裂泵等動力系統的解耦率，依據線性規劃理論方法中的多目標到達法以及解耦優化理論，并采用MATLAB自帶的fgoalattain函數來優化隔振系統的參數，通過改變物理參數和懸置原件的結構來提高系統的隔振效果。最后，通過時域仿真對優化效果進行了驗證。

壓裂車；隔振；解耦率；優化

隨著石油開采技術的快速發展，石油增產的壓裂技術得到越來越廣泛的關注[1-2]。壓裂工作屬于高壓高負荷場景下的野外工作，需要配置專門的壓裂車組，一般情況下，壓裂車的工作環境十分惡劣，且工作的持續時間較長，為滿足高壓高負荷場景下的野外工作需求，對壓裂車的性能也提出了較高的要求。而對壓裂車的發動機和壓裂泵而言，不僅自身具有較大的質量，且在進行壓裂作業時會產生很大的激振，對壓裂作業的工作環境會產生極大的影響[3-6]。

針對壓裂車的發動機和壓裂泵的振動問題，國內外學者也展開了一系列的研究，目前的研究主要集中在壓裂車振動系統的數學建模，文獻[7]利用Pro/E軟件建立了壓裂車三缸泵的三維實體模型，然后將多剛體的動力學軟件ADAMS進行導入，建立了對應的虛擬樣機模型；文獻[8]采用狀態空間法和集中參數法建立了平衡懸架、車臺發動機以及壓裂泵和車架的多體耦合動力學模型，并利用MA TLAB/Simulink軟件對壓裂車在作業執行過程中的剛度、轉速和阻尼等參數進行了耦合振動仿真分析。上述研究對壓裂車振動系統的數學模型有了一定的研究，如何優化壓裂車的隔振系統卻研究較少。因此，本文從實際工程最大化能量解耦角度出發，結合多目標到達法和解耦優化理論，采用振動系統的解耦率為隔振系統的優化目標，通過更改懸置原件的物理參數和原件結構來改善系統的隔振效果。

1 隔振優化原則

壓裂車橡膠隔振器一般具有較低的固有頻率帶。在實際工程應用中，對壓裂泵隔振系統和發動機懸置系統而言，難以實現兩者的完全解耦。因此，解耦優化的對象主要專注于和系統激勵緊密相關的自由度上。目前常用的激勵慣性解耦理論主要包括能量解耦理論和打擊中心理論。然而在石油壓裂車工作場景下，由于有限的臺上空間而致使布置十分緊湊，具有較高的空間利用率，又因為打擊中心理論對布置方式的空間大小要求極高，該方法不適用與石油壓裂車工作場景。故文中采用能量解耦法對系統的隔振進行優化。

能量解耦法中的能量解耦率是指從能量分布的視角求取不同階模態下每個坐標占取的能量比例[9]。若系統在此階的振動頻率時，振動能量只分布于一自由度之下，則系統緊緊沿著次自由度進行振動，而和其他的自由度是解耦的。在多自由度系統下，不同自由度之間是存在相互耦合的關系的，而隔振系統的優化也就是激勵作用下的不同自由度上的耦合振動解耦。

對隔振系統的整體性能而言，可從振動影響方面進行考慮分析。根據振動分析的基本理論，單自由度系統在振動情況下的振動周期為：

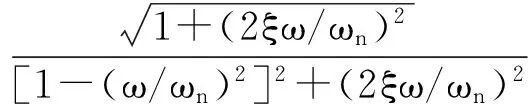
(1)

式中：ω是外部激勵作用下的頻率；ωn是系統固有的頻率；ξ是系統的阻尼比；λ是系統的頻率比。

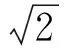
當壓裂車工作在負荷穩定的情況下時，其對應的激勵源主要為壓裂泵和柴油發動機內部不平衡的力矩和慣性力，以及因其結構本身帶來的力矩波動。振動系統具有的共振分布即是由這些激勵的所有頻率所構成，危險的共振區是在進行隔振優化時重點所需要考慮的區域。因此，從頻率方面考慮可以將振動系統的激勵源分為翻倒力矩激勵和慣性力激勵，兩者所對應的頻率分別為：

翻倒力矩的激勵頻率

(2)

式中：f1是翻倒力矩的激勵頻率；n是壓裂泵和柴油發動機的轉速；N是缸數；τ是沖擊的數量，壓裂泵沖擊數量取值為2，柴油發動機的沖擊數量取值為4。

慣性力的激勵頻率

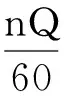
(3)

式中：f2是慣性力的激勵頻率；Q是不同階數下的激勵比例系數，一階激勵的取值Q=1，二階激勵的取值Q=2。

2 發動機懸置系統優化

2.1 目標函數

針對發動機懸置系統，其在發動機曲軸坐標系下的xyz方向具有較為理想的解耦率，而在θy和θx方向上具有較強的耦合程度，表明該方向上的發動機激勵的翻倒力矩較大，該自由度上的強耦合會很大程度上影響隔振系統的效果。因此將解耦率作為需要優化的量。選取的優化目標如下：

(4)

式中：max(Tpi)是第i階數上的最大解耦率；βi是加權系數。

自由度上的不同需求可將加權系數進行調整，反復調整加權系數的取值即可得到理想的優化結果。采用MATLAB中的fgoalattain函數來解決該類優化問題[10]，其對應的分析流程如圖1所示。

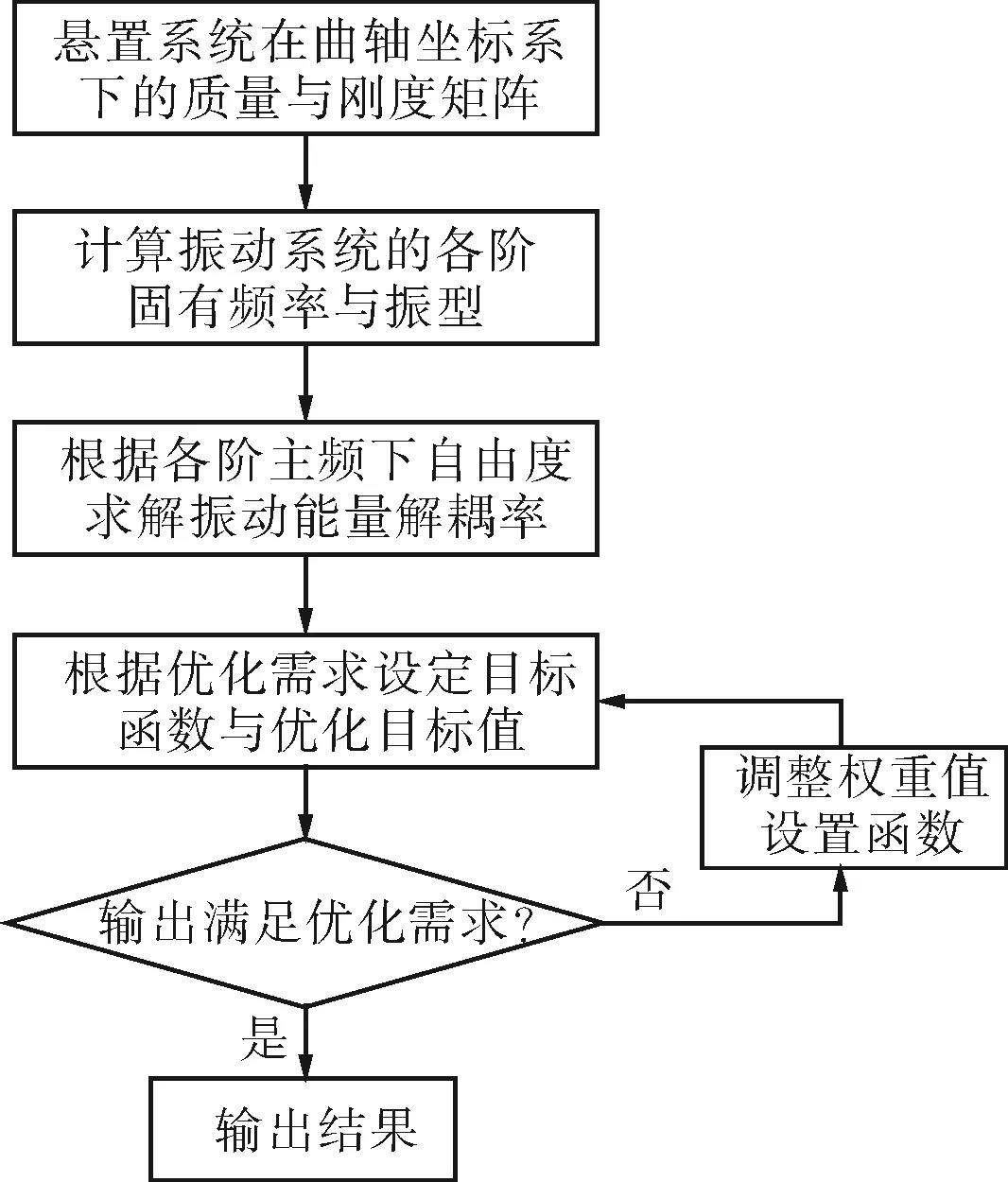
圖1 MATLAB優化流程

2.2 優化約束條件

1) 解耦率和固有頻率值分配。對于解耦率的目標取值方面，由于采用的懸置原件是橡膠懸置，因此希望優化后的解耦率目標取值至少能夠達到80%左右。對于固有頻率的分布，因為文中選取的發動機工作轉速為800～2 000r/min，則可以求出系統的工作頻率為93.3～266.7Hz。同時，發動機具有較寬的工作頻率，根據式(1)～(3)，發動機的固有頻率和翻側方向的頻率應小于66Hz。

2) 懸置元件主軸剛度約束值。較低的主軸剛度會使振動的幅度增大，而增大主軸剛度雖然能夠降低振動的幅度，但是會使懸置原件振動的傳遞率增大，進而降低了系統的隔振性能。考慮到工藝問題，通常將壓減的剛度比值取3～8，該取值范圍能夠作為線性不等式的約束條件對，即剛度值和剛度比的約束。

2.3 優化結果

在Matlab軟件中進行優化調節，能夠獲取比較合理的懸置系統的主軸剛度，如表1所示。表中，U、V、W是發動機懸置局部彈性主軸坐標系。

表1 優化后的懸置元件主軸剛度 N/mm

經過優化后的固有頻率以及對應的解耦率分別如表2所示，其中，x、y、z是發動機曲軸坐標系，θx、θy、θz是繞x、y、z方向的轉動坐標系。

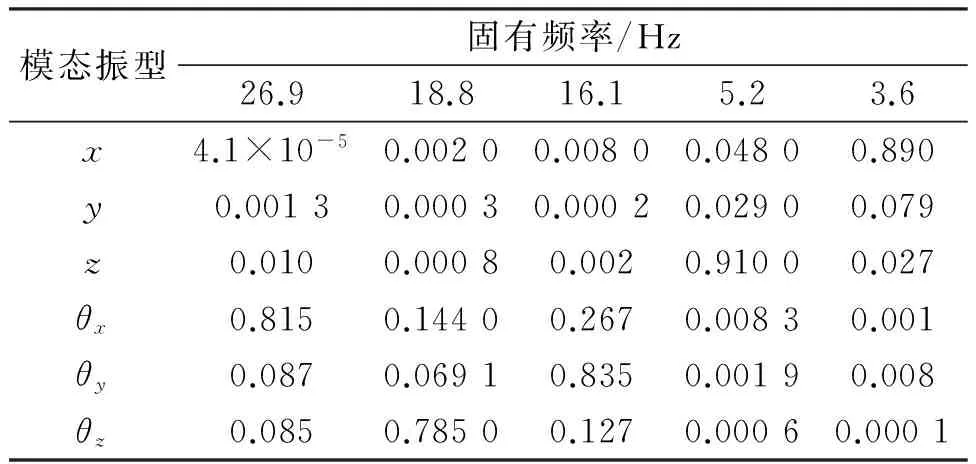
表2 優化后的懸置系統固有頻率和解耦率

根據優化后的振動特性可知，發動機懸置系統的振動分布能夠在一定程度上得到有效的改善，每個自由度上都能滿足其對應的要求。耦合模型的固有頻率及其解耦率都能夠滿足要求。因此對發動機懸置系統的剛度進行優化具有一定的意義。

3 壓裂泵隔振系統優化

3.1 目標函數

對壓裂泵系統而言，同樣的可選取優化目標如下：

(4)

式中：max(Tpi)是第i階數上的最大解耦率；αi是加權系數。

同樣的可根據自由度上的不同需求將加權系數進行調整，反復地調整加權系數的取值即可得到理想的優化結果。

3.2 優化約束條件

1) 解耦率和固有頻率值分布。壓裂泵常用的工作沖次是100～300min-1，即可以求出對應傾覆力矩的頻率為8.33～25Hz。因此，壓裂泵的側翻和豎直方向的固有頻率應不大于5.9Hz，該條件即可作為優化的約束條件。解耦率的約束條件同上述分析的發動機解耦率的約束條件是一致的。

2) 隔振系統主軸剛度的約束取值。同樣的將壓減的剛度比值取3～8，該值作為線性不等式的約束條件對剛度值和剛度比進行約束。

3.3 優化結果

同理，在Matlab軟件中進行優化調節，能夠獲取比較合理的橡膠隔振系統的主軸剛度，如表3所示，其中P、Q、R是壓裂泵隔振器局部彈性主軸坐標系。

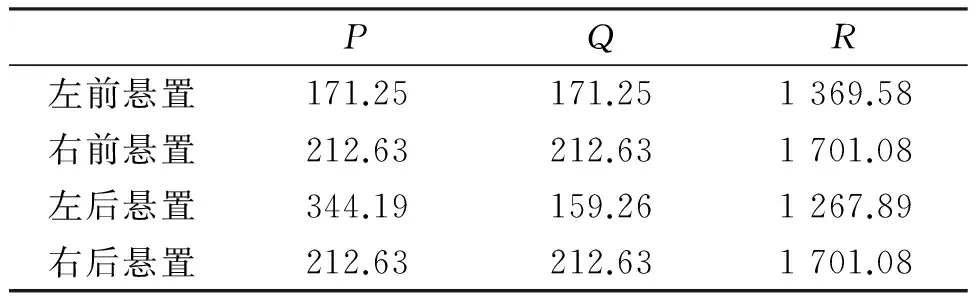
表3 優化后的隔振元件主軸剛度 N/mm

隔振元件經過優化后的固有頻率以及對應的解耦率分別如表4所示，其中x、y、z是壓裂泵曲軸坐標系，θx、θy、θz是繞x、y、z方向的轉動坐標系。

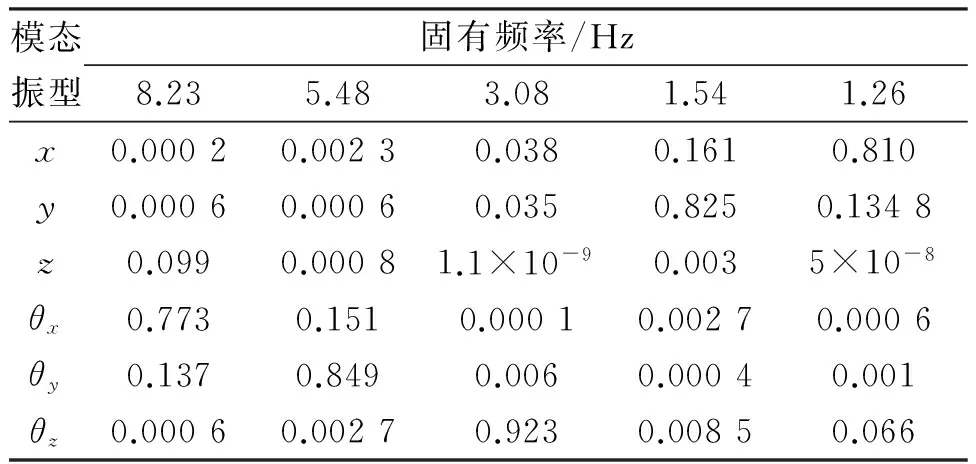
表4 優化后的隔振元件固有頻率和解耦率

同理，通過優化之后，隔振元件系統的振動分布能夠在一定程度上得到有效改善，每個自由度上都能滿足其對應的要求。優化后的隔振元件固有頻率及其解耦率都能夠滿足要求。因此對壓裂泵隔振元件系統的剛度進行優化也具有一定的意義。

4 結論

本文對石油壓裂車動力系統隔振進行了優化研究，優化的目標為提高柴油發動機和壓裂泵的振動解耦率，根據能量解耦理論和多目標到達法，并采用MATLAB軟件中的fgoalattain函數來優化隔振系統的參數。對隔振效果的優化進行了仿真驗證，結果驗證了優化結果的有效性。

[1] 程興生，盧擁軍，管保山，等.中石油壓裂液技術現狀與未來發展[J].石油鉆采工藝，2014(1)：1-5.

[2] 姜海洋.試論石油開發中體積壓裂技術的應用[J].化工管理，2015(30)：135-135.

[3] 桑猛.大功率壓裂車車架承載能力研究[D].大連：大連理工大學，2013.

[4] 曹桐軍，趙靜，邱帥迪，等.懸置膠墊剛度變化對發動機隔振效率的影響研究[J].企業技術開發月刊，2016，35(16)：43-45.

[5] 高媛，王紅，單東升.2500型壓裂車車架結構多目標拓撲優化設計[J].石油礦場機械，2015，44(5)：49-53.

[6] 王紅玲，單東升，高媛.壓裂車車架結構尺度優化設計方法研究[J].石油礦場機械，2015，44(11)：51-55.

[7] 馬曉偉，劉健，孫延迪，等.基于ADAMS的壓裂車三缸泵振動分析[J].機電工程，2014，31(11)：1415-1418.

[8] 王川，謝真強，王國榮，等.壓裂車作業過程耦合振動仿真分析[J].系統仿真學報，2016，28(7)：1586-1592.

[9] 陳永瑞.基于Adams與Isight的輕卡動力總成懸置系統優化設計[D].青島：青島理工大學，2015.

[10] 張煒，李華.微機電系統微彈簧優化設計方法[J].探測與控制學報，2014(6)：11-14.

Research on Vibration Isolation Optimization of Power System for Oil Fracturing Vehicle

QIU Zongbin

(Changqing Downhole Technical Service Company，CCDC，Xi'an 710018，China)

Aiming at the vibration problem of diesel engine and fracturing pump and other dynamic systems for oil fracturing vehicle，a parameter optimization method of vibration isolation system is proposed.The optimization goal of this method is to improve the decoupling rate of diesel engine and fracturing pump.According to the multi-objective arrival method and the decoupling optimization theory in the linear programming theory method，the fgoalattain function of MATLAB is used to optimize the parameters of the vibration isolation system，and the vibration isolation effect of the system is improved by changing the physical parameters and the structure of the originals.Finally，the optimization effect is verified by time domain simulation.

fracturing vehicle；vibration isolation；decoupling rate；optimization

1001-3482(2017)04-0065-04

2017-01-11

邱宗斌(1975-)，男，甘肅涇川人，工程師，主要從事油田工程服務、試油壓裂作業工作。

TE

A

10.3969/j.issn.1001-3482.2017.04.016